框架预应力锚杆支护结构地震永久位移计算

刘东汉

摘 要：地震永久位移是评定结构抗震性能和安全性能的关键因素，尤其是对框架预应力锚杆支护结构这种复杂的柔性支护结构来说更加关键，其数值取决于结构的材料特性、形式及地震作用的强度等因素。因此，研究支护结构在地震作用下的永久位移对提高支护结构的抗震能力具有重要作用。文章针对框架预应力锚杆支护结构地震永久位移的计算方法展开研究，探究了该结构在地震作用下的变形规律和抗震能力，提出了关于永久位移可行性计算方法。文章主要运用拟静力法、极限分析上限法等理论计算方法，利用极限分析上限法推导得出了框架预应力锚杆支护结构地震屈服加速度，并根据该参数计算了结构的地震永久位移。通过MATLAB编程软件理论计算公式进行计算，并与数值模拟分析结果进行对比，验证了公式的有效性与正确性，可为支护设计提供一定的依据。

关键词：框架预应力锚杆；支护结构；极限分析上限法；地震永久位移；有限元模拟

中图分类号：TU432 文献标志码：A DOI：10.3969/j.issn.1672-6375.2024.5.009

0 引言

支护结构的变形特性对于支护结构的设计和施工至关重要。通过研究框架预应力锚杆支护结构的变形规律，可以为结构设计提供基础数据，使结构能够满足安全稳定的要求。

朱彦鹏等[1]考虑了结构与土体的相互作用，依据施工过程，将眶锯预应力锚杆设计工作分为开挖和工作2个阶段，同时提出一种可以控制侧向位移的设计方法，能够确定施加预应力的大小，根据该方法对实际工程进行设计，得出结论：确定合理的锚杆预应力大小是不可或缺的，这对框架预应力锚杆的设计至关重要。周勇和朱彦鹏[2]认为顶部位移是重要的变形控制指标，根据梯形土压力模型，通过力法计算支护结构的顶部静力位移，并对施工荷载、第一排锚杆到坡顶的距离、锚杆水平间距以及竖向间距等因素对顶部位移的影响进行分析。周勇和朱彦鹏[3]考虑基坑开挖的影响，将锚杆自由段视为弹簧，将开挖阶段的支护结构视为底端铰接，基于这种假设将坡面水平的计算简化，同时以一实际工程为例进行计算，得出了较为符合的结果，并依据几何模型，进行了室内模型试验，实测结果与理论计算结果在总体趋势上较好地吻合。

当前，针对地震作用下框架预应力锚杆支护的边坡永久位移计算研究还较少，尚需深入探索。目前的研究大多是基于振动台的室内试验，对于地震作用框架预应力锚杆支护边坡永久位移计算方法的研究还略显不足。因此，地震作用下框架预应力锚杆支护边坡永久位移的计算方法仍然需要进一步探索。

文章针对框架预应力锚杆支护边坡进行了研究，主要包括以下几个方面：（1）总结框架预应力锚杆支护边坡的基本特征和变形机理；（2）基于拟静力法和极限分析上限法，计算地震作用下边坡的外力做功与内能耗散，从而得出地震屈服加速度，最后通过计算得出了地震作用下框架预应力锚杆支护边坡的永久位移；（3）基于某工程实例，将计算结果与模拟数值进行对比，验证计算方法的可靠性和正确性，为边坡加固工程设计提供了良好的借鉴。

1 框架预应力锚杆支护结构基本概述

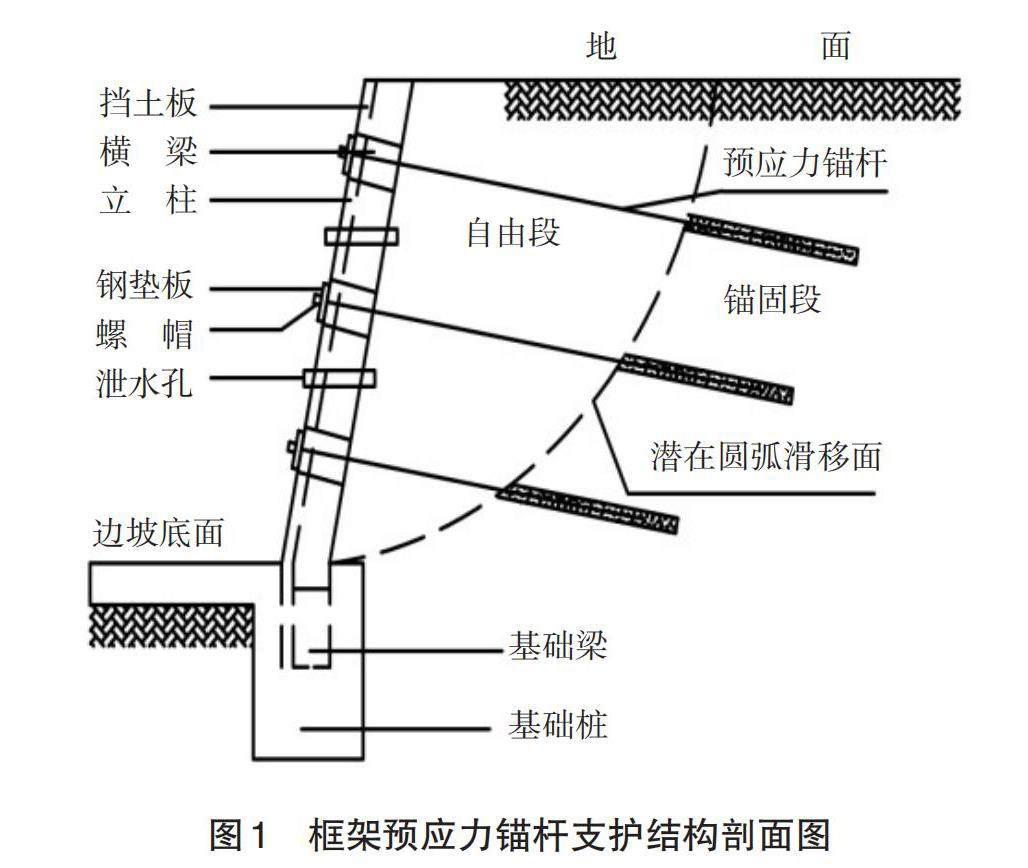
框架预应力锚杆结构作为一种新型的边坡挡土结构，旨在提高边坡土体力学性能[4]。该结构由挡土板、框架、锚杆及墙后土体组成，利用它们的协同作用来实现支挡作用。相较于传统支挡结构，该结构具有更多优势，其剖面图如图1所示。

在设计框架预应力锚杆支护边坡时，需要考虑多个因素，包括挖掘场地的类型、边坡支护结构类型、支护结构类型，以及施工条件等[5]。支护结构可采用高强度钢材或混凝土材料制成。这些设计措施的目的是提高边坡支护结构的稳定性和安全性，以确保其能够有效地抵御挖掘过程中的土压力，并为工程建设提供可靠的支撑保障。

2 极限分析上限法

20世纪50年代，Drucker等提出了与屈服条件有关的流动法则，基于速度场与静力场的结合，建立了极值理论并证明了极限分析上、下限定理。该定理因其简便、适用性强，深受广大学者们的喜爱。极限分析法最大的特点和优点是对研究对象的几何形状没有要求，无论是怎样的不规则模型，模型上的荷载如何复杂，运用极限分析定理都可以求得一个与实际状况较为相符的计算结果。除此之外，该方法在实际工程应用中也较为简单，可将工程中的破坏模式以几何图形的形式表达。经过诸多学者对极限分析法的改进、研究及实际工程中的应用，认为该方法比较可靠，可以运用于实际工程[6]。

在极限分析理论中，通常会忽略材料的应力-应变图中的应变软化过程（图2），但在实际工程中，绝大部分土体的应力-应变图在到达最大值后，会随着应变的增加而进入软化阶段，最终出现残余应力的表现。因此，极限分析定理中所假设的理想刚塑性材料是指应力达到屈服后，随着应变的不断增加，应力不发生变化。虽然理想刚塑体材料是一种理想状态，但是在岩土问题中，该假设所得到的结果比其他假设的结果更加合理。

材料进入塑性阶段后，其应力-应变关系不再是一一对应，而材料的屈服准则则是判断其由弹性阶段进入塑性阶段的依据。经过试验研究得出不同应力路径下材料的应力-应变关系，将屈服点连接形成空间曲面，即材料的弹塑性分界面。常见的屈服准则有Mohr-Coulomb、Von Mises、Tresca等，岩土工程中常用Mohr-Coulomb屈服准则。当材料发生塑性流动时，其屈服函数可以用一个表达式来描述：

在Mohr-Coulomb屈服准则中，塑性流动在土体的任意处都可发生，此时，应该满足以下条件：τ=c+σtanφ （2）

土体的剪切应力值与正应力σ及土体的黏聚力c呈线性关系，式中c、φ为常数，φ为土体内摩擦角。

将式（2）改写为主应力的形式：

确定塑性变形的应变增量方向是流动法则在塑性增量理论中的重要内容，而与应力增量方向不同是材料发生塑性变形的一般情况。因此，在塑性增量理论中，流动法则的研究非常关键。

流动法则是指材料在一定的应力状态下发生塑性应变时，材料应力的大小和方向的一般规律和规定，流动法则的确定是建立在材料的本构关系和塑性行为规律的基础上。材料的本构关系是指在一定的应力状态下，应变之间的关系，有线性关系和非线性关系两种。

1928年，Mises提出了弹性势的概念，Mises认为，塑性流动状态也有与弹性势类似的函数，就是塑性势。其函数表达式为：

材料在屈服后进入塑性流动状态，应力不变，而应变则会无限增大。在塑性流动状态中，材料的应变可以间接地由塑性势函数表达，通过塑性应变增量的大小和方向来确定。此时，塑性势函数可以用来表示塑性应变增量的大小函数：

式中：dλ为非负的塑性乘子。

通过公式（5）可以确定塑性应变增量的方向。若屈服面F与塑性势能面Q重合，由F=Q所得到的关系称之为加载条件相关联的流动法则。相关联流动法则的函数关系如下可知：

根据土体的本构关系，塑性极限分析上限法可以直接计算出土体极限状态下的荷载和速度，而忽略了材料应变软化过程。假设在任意可行的速度场中，应变场率和速度场内外力做功与内能耗散相等，可以确定荷载，其值一定大于或等于实际的极限荷载。这个定理称为极限分析上限定理，可以使用虚功方程表达：

3 地震荷载作用下边坡地震永久位移拟静力计算

3.1 计算假定

在研究预应力锚杆边坡地震位移时，采用极限分析上限法，将地震荷载的加速度系数均匀分布于墙高，并将其视为惯性力进行考虑。在计算过程中，需要结合相关研究材料和结果，并满足以下假定：

（1）研究土体符合相关的流动法则；

（2）假设预应力锚杆边坡的滑移面为对数螺旋线滑移面，并且最危险滑移面通过墙底；

（3）墙后填土均匀，在边坡破坏时锚杆达到极限值；

（4）满足平面应变假设。

3.2 计算模型分析

将整个滑动楔体ABC看作绕着旋转中心O点转动的旋转体，旋转角速度为Ω，边坡高度为H，h f 为锚杆高度。假设边坡的土体容重为γ，内摩擦角为φ，土体黏聚力为c，地震水平加速度系数为k h ，竖向地震加速度为k v ，采用塑性力学上限法分析墙土的动力特性，为了计算简便，将OB、OA的倾角分别假定为θ B 和θ A ，依据图3的计算模型可以得出对数螺旋滑移面的方程为：

式中： r A 为对数螺旋滑移面上与水平方向夹角为 θ A 时的极径，即OB的长度为

由此可以得出OB的长度为：

根据边坡模型的几何关系可以得出L（AC段长度）和H的表达式为：

式中：β为边坡倾角。

3.3 重力作用下边坡外功计算

3.3.1 边坡OAB部分求解

对OAB部分土体取一微元体进行分析计算，由图4可得OAB区域土体重力所作的外功率。

由图4可得到微元体OAB所作功率为：

将dw 1 沿着OAB区域进行积分计算，即可得到OAB土体所做外功率w 1 ：

其中：

将式（13）代入式（12）中可得：

由此可得，式（14）为OAB区域内土体自重所作的功率。

3.3.2 边坡OAC部分求解

对OAC部分土体进行分析计算，由计算简图可得OBC区域土体重力所作的外功，如图5所示。

同理，即可得到OAC部分土体所作功率为：

由此可得，式（15）为OAC区域内土体自重所作的功率。

3.3.3 边坡OBC部分求解

对 OBC 部分土体进行分析计算，由图 6 可得OBC区域土体重力所作的外功率。

同理可得到微元体OBC所作功率为：

至此，已经求得重力所做功的计算式，由叠加法可得土体ABC所作功的大小为：

3.3.4 地震荷载做功

基于地震的复杂性，目前学者们在研究地震时常常运用拟静力法来研究地震工程问题。文章在分析地震作用时使用拟静力法考虑地震作用。

将水平和竖直地震作用分别用k h 和k v 来表示。

式中：ξ是k v 相对于k h 的比例系数。

由图2可知外功率做功除了重力以外还有水平地震荷载和竖向地震荷载。首先考虑竖向地震荷载，由于竖直方向的地震荷载与重力方向一致或相反，则竖向地震荷载的做功可表示为：

其中f 1 、f 2 、f 3 表达式为（13）、（16）、（18）。

对于水平地震荷载的计算可以参照上文计算方法得到：

其中土体OAB在水平地震荷载作用下所做的功 w k h -5 以及f 4 的表达式如下式：

土体 OAC 在水平地震荷载作用下所做的功w k h -5 以及f 5 的表达式如下式：

土体 OBC 在水平地震荷载作用下所做的功w k h -6以及f 6 的表达式如下式：

将式（24）、（25）、（28）代入（22）中，即可求得土体ABC在水平地震荷载作用下做的功。

3.3.5 锚索拉力做功

假设T为预应力锚杆的锚固值，锚杆与水平面的夹角为α，确定边坡上锚杆位置的角度为θ M ，边坡锚杆位置距坡底距离为h f ，锚杆与坡面交点为M，锚杆与对数螺旋滑移面的交点为N。M点的直角坐标系下的位置为（x M ，y M ），在极坐标系中对应的角度为θ M ，N点的直角坐标系下的位置为（x N ，y N ），在极坐标系中对应的角度为θ N 。由几何关系可知：

基于对数螺旋线破坏面，当锚杆的拉力作用在M点时，锚杆拉力T做功的能量方程为：

基于对数螺旋线破坏面，当锚杆的拉力作用在N点时，锚杆拉力T做功的能量方程为：

由已知的研究结果可知式（32）、式（33）的计算方法是一致的，文章在计算锚杆拉力T所作的外功时，选用（32）进行计算。

3.4 地震作用下边坡内能耗散计算

假设边坡内部的变形一致，即塑性破坏时不产生能量损耗。边坡土体沿着对数螺旋线面破坏产生的内能耗散是由土体黏聚力所产生的能量。在计算时对数螺旋形上取一微元体，其微分长度dl为：

因此，在整个对数螺旋滑移面上土体黏聚力c所产生的能量耗散率w c 的表达式为：

将 r（θ）=r A e（θ-θ A ）tanφ和 v（θ）=rΩ 由此可得，土体黏聚力所作内功为：

3.5 框架预应力锚杆支护结构地震屈服加速度系数

根据极限分析法，当机构处于临界滑动状态时，其外力做功与内能耗散相等时，支护结构处于极限平衡状态，根据极限分析可得：

W g +W kh +W kv =W r +W t （37）

当处于极限平衡状态时，定义水平地震系数k h为结构地震屈服加速度k s ，此时可得出支护结构破坏的不安全上限值，支护结构所对应的地震加速度为支护结构的地震屈服加速度k s ，其表达式为：

将式（22）、（24）、（25）、（31）、（36）、代入上式（38）中可得框架预应力锚杆支护结构地震屈服加速度系数：

式中：地震屈服加速系数为k s 。

框架预应力锚杆支护结构在不同的滑移面上有不同的解，为了边坡的安全，应求得最小屈服加速度解，从而得到最危险滑移面，公式（39）中有θ A 、θ B 2个未知参数，将求解屈服加速度问题变为求解（39）的最小值问题，则有：

为了求得框架预应力锚杆支护结构边坡处于临界状态时对应的地震的屈服加速度系数k s ，（40）方程应满足如下约束条件：

因此，根据式（39）、（40）、（41）联立后即可确定θ A 、θ B ，代入（39）中即可确定最小地震屈服加速度系数k s-min ，即在下一节中计算永久位移时框架预应力锚杆支护结构边坡的地震屈服加速度系数。

3.6 框架预应力锚杆支护结构地震永久位移计算

在Newmark理论[7]中，假定滑块的位移是被认为是永久位移，将地震时的瞬时地震加速度设为k（t），当k（t）＜k s 时，边坡不会产生位移；当k（t）=k s 时，边坡处于极限状态；当k（t）＞k s 时，边坡开始移动。以图7为例，假设地震波形为正弦波，当k（t）增大时，边坡开始加速，产生位移累计，直至地震加速度最大值；当k（t）逐渐减小时，边坡开始减速，直到k（t）=k c ，此时，边坡速度为0，位移为0。

根据前文分析，可以得知地震时某一时刻的边坡加速度：

对式（42）进行关于t的二次积分，即可得出地震作用下框架预应力锚杆支护结构边坡永久位移的公式：

通过（43）可得，边坡的永久位移与地震加速度k（t）、地震屈服加速度k s 有关。因此，在计算地震永久位移时，仅需要确定地震屈服加速度以及地震波即可求得地震作用下框架预应力锚杆支护结构边坡永久位移。

4 算例验证

4.1 工程概况

地震水平加速度为 0.3 g，竖向地震及速度取0.1 g。在进行 PLAXIS 3D 进行数值模拟时，选用EI-Centro波对边坡进行地震作用下的数值模拟，其地震波图如图8所示。

4.2 理论计算结果

根据文章的计算方法，基于上一节中的设计参数，得出了边坡永久位移的结果，将该结果与PLAX?IS 3D 模拟得出的位移结果进行对比分析，运用MATLAB软件所求得的k s =0.136，所求的永久位移和模拟所得的永久位移见表1。得出以下结论：文章计算方法所得到的边坡地震永久位移值和PLAXIS 3D模拟所得的永久位移值相差不大，有限元软件所得的永久位移偏大，因此文章的计算方法偏向于保守。

如图9、图10、表1所示，在静力和地震作用下，采用有限元软件进行数值模拟计算得到的边坡位移峰值变化曲线大致相似。中下部结构的位移值较大，而顶部位移值和底部位移值略小于中部位移值。当考虑地震作用时，整体上边坡位移值增加。然而，由于框架预应力锚杆支护结构中的各体系之间相互协同作用分担了地震过程中边坡内的剪力，因此边坡位移峰值变化的趋势并没有太大变化。

5 结论

文章针对框架预应力锚杆支护结构边坡的位移展开研究，主要运用拟静力法和极限分析上限法对地震作用下的边坡位移进行研究，并且通过工程实例对所得的计算方法进行了验证，得出以下几点结论：

（1）运用拟静力法和极限分析上限法对边坡位移进行计算，首先确定了框架预应力锚杆支护边坡的计算模型，随后依据计算模型计算了外力做功和内能耗散情况，求得边坡地震屈服加速度，最后得出地震作用下边坡永久位移的计算公式。

（2）通过MATLAB编程软件对理论计算公式进行计算，并与数值模拟分析结果进行对比验证，结果表示，该计算方法所得结果相较于有限元模拟值偏大，验证了公式的有效性与正确性，可为支护设计提供一定的依据。

（3）数值模拟分析表明，框架预应力锚杆支护结构在静力和地震2种状态下都能够控制边坡的位移，对一定程度上抑制边坡产生的位移起到了重要的作用。然而，在地震作用下，框架预应力锚杆支护结构的控制作用并不足以完全抵挡边坡的位移变形。

参考文献：

[1]朱彦鹏，郑善义，阎茹，等. 黄土边坡框架预应力锚杆支挡结构的设计研究[J]. 岩土工程学报，2006（S1）：1582-1585.

[2]周勇，朱彦鹏. 框架预应力锚杆边坡支护结构顶部静力位移求解及其所受影响因素分析[J]. 兰州理工大学学报，2008（2）：113-117.

[3]周勇，朱彦鹏. 框架预应力锚杆柔性支护结构坡面水平位移的理论分析与模型试验研究[J]. 岩石力学与工程学报，2010，29（S2）：3820-3829.

[4]韩爱民，李建国，肖军华，等.预应力锚杆框架梁的支护力学行为研究[J]. 岩土力学，2010，31（9）：2894-2900.

[5]王长荣. 黄土地区框架预应力锚杆支护结构研究综述[J].中国建材科技，2010，19（6）：76-80.

[6]陈祖煜. 土力学经典问题的极限分析上、下限解[J]. 岩土工程学报，2002（1）：1-11.

[7]Newmark N M. Effect of Earthquake on dams and em?bankment[J]. Geotechnique，1965，15（2）：139-160.

Calculation of Permanent Seismic Displacement of Frame Prestressed Bolt Support Structure

LIU Donghan

（Gansu Wuhuan Highway Engineering.，Ltd，Lanzhou Gansu 730050，China）

Abstract： ： The seismic permanent displacement is a key factor to evaluate the seismic performance and safety performance of the structure， especially for the complex flexible support structure such as the frame prestressed bolt support structure， and its value depends on the material properties of the structure， the form and the strength of the seismic action. Therefore， studying the permanent displacement of the support structure under the action of earth?quake has an important influence on improving the seismic capability of the support structure. This paper studies the calculation method of the seismic permanent displacement of the prestressed anchor structure of the frame， ex?plores the deformation rule and seismic capability of the structure under the action of earthquake， and puts forward the feasibility calculation method of the permanent displacement. This paper mainly uses the pseudo-static method，limit analysis upper limit method and other theoretical calculation methods to derive the seismic yield acceleration of the frame prestressed bolt support structure， and calculates the seismic permanent displacement of the structure according to the parameter. The theoretical formula is calculated by MATLAB programming software， and the re?sults are compared with the numerical simulation analysis to verify the effectiveness and correctness of the formula，which can provide a certain basis for the support design.

Key words： ： frame prestressed bolt; supporting structure; upper limit analysis method; seismic permanent dis?placement; finite element simulation