某柱塞偶件的结构非概率可靠性分析

2024-06-22吕星飞段逸凡吕帆张子威聂思佳

机械 2024年5期

吕星飞段逸凡吕帆张子威聂思佳

摘要：某型喷油泵内柱塞偶件易发生卡滞故障，导致柴油机的运行存在重大安全隐患。通过对柱塞偶件建模并分析其工作原理，确定了引起卡滞的重点部位，同时结合有限元仿真分析出故障产生原因是工况下偶件的结构变形。基于区间分析方法建立柱塞偶件结构非概率可靠性模型，针对功能函数构建神经网络代理模型，通过遗传算法求出可靠性指标η。研究结果表明，配合间隙为3 μm的原方案对应η为0.97393，结构可能发生失效；若改为3.5 μm，η提升为2.3391，结构处于安全状态，其非概率可靠性得到较大提高。该研究对柱塞偶件的设计改良具有一定的参考作用。

关键词：柱塞偶件；有限元分析；非概率可靠性；区间分析

中图分类号：TK4 文献标志码：A doi：10.3969/j.issn.1006-0316.2024.05.005

文章编号：1006-0316 （2024） 05-0035-08

Structural Non-Probabilistic Reliability Analysis of Plunger Assembly

LYU Xingfei1，DUAN Yifan2，LYU fan1，ZHANG Ziwei1，NIE Sijia2

（ 1. China North Engine Research Institute， Tianjin 300400， China; 2. School of Mechanical and Electrical Engineering， University of Electronic Science and Technology of China， Chengdu 611731， China ）

Abstract：The plunger assembly in a certain type of fuel injection pump is prone to jamming， which leads to significant safety risks during the operation of the diesel engine. By modeling the plunger assembly and analyzing its working principle， this paper identifies the key parts that cause the jamming. At the same time， through the finite element analysis， it is found that the cause of the failure is the structural deformation of the plunger assembly under the working condition. A structural non-probabilistic reliability model of plunger assembly is established based on interval analysis method in this paper. Then the neural network is used to construct the performance function， and the reliability index η is calculated by genetic algorithm. The results show that when the clearance fit is 3 μm， the corresponding η of the original design is 0.97393， and the structure may fail. When the gap is changed to 3.5 μm， the η increases to 2.3391， which indicates that the structure is safe， and its non-probabilistic reliability is greatly improved. The conclusion provides valuable insights for the design of plunger assembly.

Key words：plunger assembly；finite element analysis；non-probabilistic reliability；interval analysis

柱塞偶件由柱塞和柱塞套组成，是柴油机内一对极其重要的精密偶件，被装配在喷油泵单元内，承担着提高燃油压力的作用[1]。某型号直列式喷油泵在生产使用过程中发生了柱塞偶件卡滞频次较高的问题，柱塞卡滞会导致柴油机失控，甚至造成柴油机飞车事故，危害较严重，因此针对该柱塞偶件的可靠性研究引起了高度重视。传统的概率可靠性理论需要大量数据的支撑以描述随机变量的概率分布，但该型号喷油泵由于引进时日尚短，应用验证不充分以及相应的保密限制，难以获取概率可靠性分析所需要的大量数据信息。有研究表明，概率可靠性的计算结果对随机变量概率参数很敏感，当没有足够的数据来获取变量的确切分布时，采用主观假设方式可能会对可靠性计算结果造成极大误差[2-3]。但从已有的数据来看，获取不确定因素的界限较为容易，因此针对柱塞偶件的非概率可靠性分析具有一定的可行性。

非概率可靠性理论由Ben-Haim等[4]于20世纪90年代首次提出，采用系统能承受的最大不确定性程度来衡量其非概率可靠性。郭书祥等[5]提出一种基于区间分析的非概率可靠性度量方法，根据指标η与区间[-1，1]的关系来确定结构是否失效。屠义强等[6]将结构系统非概率可靠性与区间有限元理论结合，提出的新方法能正确识别具有多个失效模式的结构系统并分别给出其非概率可靠性指标。郭书祥等[7]结合区间变量的运算规则，提出了根据不同函数形式可分别采用定义法、转换法和优化法来求解η。宋利锋等[8]将非概率可靠性优化方法应用于机翼的结构优化，使计算效率得到提升。高泽民[9]利用可靠性理论分析了燃油杂质对柱塞偶件造成的磨损影响并提出控制措施。彭琦等[10]针对柱塞偶件卡滞问题，通过建立故障树发现原因为拧紧力矩不合适，随后提出改进措施并通过试验验证。赵晋[11]以高压共轨喷油器为研究对象，建立柱塞偶件的热流固耦合模型，采用两种改进措施有效减小了柱塞偶件的变形量。综上，目前针对柱塞偶件的非概率可靠性研究较少，同时研究对象大都为轴向式[12-13]和高压共轨式[14-16]喷油泵，然而直列式是较为成熟的结构，在机械装备中应用较多，因此有必要对其故障现象开展相关研究。文中从柱塞偶件的结构变形量出发，将装配时的拧紧力矩、工作时的供油压力以及结构尺寸参数作为影响变形的不确定参数，基于区间分析建立柱塞偶件的结构非概率可靠性模型，求出其可靠性指标并展开相关分析。

1 柱塞偶件有限元仿真

根据该型喷油泵的拆检情况，柱塞偶件卡滞现象主要是零件表面片状变色和局部烧结，可归因于柱塞套内孔与柱塞外圆尺寸或几何形状匹配不合理。喷油泵运行时，柱塞偶件在工作载荷的作用下会产生形变。若柱塞和柱塞套的配合间隙过小，将导致柱塞头部与柱塞套压油出口处相互摩擦，如图1所示。

图1展示了该柱塞头部出现的表面变色情况。此外，即使偶件没有因此发生卡滞故障，也会由于柱塞顶部计量棱角的磨损带来供油量的变化，对偶件的使用寿命造成显著影响。若偶件的配合间隙过大，则会导致漏油降压，同样影响柴油机的正常工作，因此合理设计配合间隙的大小很重要。

本文利用SolidWorks建立柱塞偶件三维模型，其中柱塞和柱塞套的相对位置关系如图2所示。柱塞随着凸轮的转动在柱塞套内上下运动，实现进油、供油和回油功能。紧压空心螺栓与柱塞套为螺纹副连接，下端面设计为刃口，装配后切入柱塞套内端面以实现密封作用。柱塞偶件基本工作原理是当燃油通过喷油泵低压油道进入柱塞套后，在凸轮的作用下，柱塞向上挤压柱塞腔内燃油，当燃油压力升高到一定阈值时，位于紧压空心螺栓内的出油阀被挤开，燃油进入高压管路最终到达喷油器。

当柱塞偶件处于供油状态时，其内部形成一个密封腔，腔内主要受到三个力导致其结构发生形变，分别是紧压空心螺栓刃口对柱塞套

内端面的压力，高压燃油对柱塞套内表面的压力以及高压燃油对柱塞表面产生的压力，如图3所示。

图3 密封腔受力示意

为便于设置载荷条件并提高仿真效率，需对紧压空心螺栓进行简化处理。要实现螺栓与柱塞套的配合，对紧压空心螺栓施加的拧紧力矩主要转化为两部分，分别是克服螺纹副相对转动的阻力矩以及螺栓下端面与垫圈上表面间的摩擦阻力矩。通过力学分析建立相应的转化公式后，得到不同拧紧力矩下柱塞套内端面所受正压力如表1所示。后续分析可用施加在柱塞套内端面上的正压力来替代螺栓拧紧力矩。

将模型导入ANSYS，按实际情况设定柱塞偶件的密度、杨氏模量和泊松比等材料参数后进行网格划分，对重点区域设置局部细化，得到精度合理的网格划分结果剖面如图4所示，该有限元模型总计174 011个单元以及296 562个节点。

对柱塞套内端面所受正压力以及柱塞偶件供油压力进行载荷条件设置，图5和图6的红色区域分别展示了两种载荷的作用范围。

完成载荷约束条件的设置后，对柱塞偶件进行结构有限元仿真。表2为在不同供油压力下的柱塞偶件最大应力和应变情况，针对应力的多次计算结果表明，各种载荷条件下仿真得出的最大应力均小于偶件材料25Cr5MoA钢的屈服强度1032 MPa[17]，因此材料强度满足工作需求。

为进一步确定卡滞失效的原因，以下分析工作时偶件形变带来的影响。图7为拧紧力矩150 N·m及供油压力100 MPa条件下，柱塞偶件在X方向的变形情况。

由图7可知，由于螺栓刃口对柱塞套内端面产生的下压作用，内端面与刃口接触部位实际上有Y轴负方向的位移，但该方向形变不影响柱塞偶件的卡滞。柱塞头部区域的形变结果表明，螺栓预紧力使柱塞套内端面发生缩口变形，油液压力使柱塞发生外径膨胀，因此偶件发生卡滞是柱塞套内径缩小和柱塞外径扩大的综合作用，因此只需考虑偶件在X-Z平面的形变。此外，由于柱塞偶件结构近似中心对称，可用结构在X方向位移来代替其在整个X-Z平面的位移以简化分析。

图7中柱塞头部膨胀的最大形变为2.74 μm，柱塞套相应缩口处的形变为0.14 μm，得到柱塞偶件在工作时配合间隙减小了2.88 μm，由于目前该型号柱塞偶件的设计间隙为3 μm，结合制造和装配时存在的随机误差，可能会造成偶件卡滞，进而出现如图1所示的变色和拉痕。

2 结构非概率可靠性分析

通过结构仿真得知，在拧紧力矩150 N·m及供油压力100 MPa条件下，柱塞偶件配合间隙减少量十分接近设计间隙，一旦其变化量超过设计间隙最小值，柱塞偶件将发生卡滞故障。在实际工程中，由于各种不确定性的影响，柱塞偶件所受载荷、尺寸等参数不是固定值，而是一系列随机变量。由于缺乏充足的数据信息，相关参数采用区间变量进行建模，对柱塞偶件的非概率可靠性进行分析。

2.1 区间分析

在结构可靠性分析中，用区间对变量进行建模不需要太多数据信息，只要能够获取到随机变量的取值范围，因此对于数据信息较少的情况下应用较为方便。

假设变量P为结构系统的输入不确定参数之一，通过参数评估得知该变量最小可能取值

为，最大可能取值为，那么变量被称为区间变量，其中是

一个区间。通过变换可得：

（1）

（2）

式中：为区间的均值；为区间的离差。

可表示为：

（3）

若有标准化区间变量，其中区间，则和可表示为：

（4）

（5）

通过对柱塞偶件及其有限元模型输入参数分析得知，影响配合间隙变化量仿真结果的不确定参数主要有3个，分别是拧紧力矩M、供油压力P和刃口宽度W。利用区间分析方法对其进行不确定建模，得到3个区间变量分别为：

（6）

（7）

（8）

式中：；其他变量参数信息见表3。

2.2 结构非概率可靠性分析

假设向量为结构系统的输入不确定参数（如结构尺寸、载荷量以及装配特性等）集合，基于区间分析可将向量表示如下：

（9）

设输入参数为向量的结构系统的功能函数表示为：

（10）

功能函数是由结构失效准则确定的，当

时，结构处于安全域，当时，结构处于失效域，当时，结构处于临界状态。由区间

分析可知，基于结构功能函数的响应值同样

为区间变量，假设的均值为，离差为，则非概率可靠性指标为[5]：

（11）

由式（11）可知，当时，对于区间变量的任意取值均有，结构处于安全状态；而当时，在区间变量的整个定义域内结构均处于失效状态；当时，无法直接确定结构是否安全或失效。根据式（10）和式（11），结构系统的安全程度与的值成正比。

在柱塞偶件非概率可靠性分析中，其关键失效模式为偶件配合间隙过小引起的工作变形卡滞失效，因此功能函数定义为：

（12）

式中：为柱塞偶件的设计间隙，目前该型柱塞偶件的设计间隙为3 μm；为通过有限元仿真得出的当变量参数为时的

柱塞偶件配合间隙减少量。

通过式（12）可知变量为区间变量，当变量的值大于时，结构功能函数

值小于0，柱塞偶件发生卡滞失效，反之则偶件结构处于安全域。

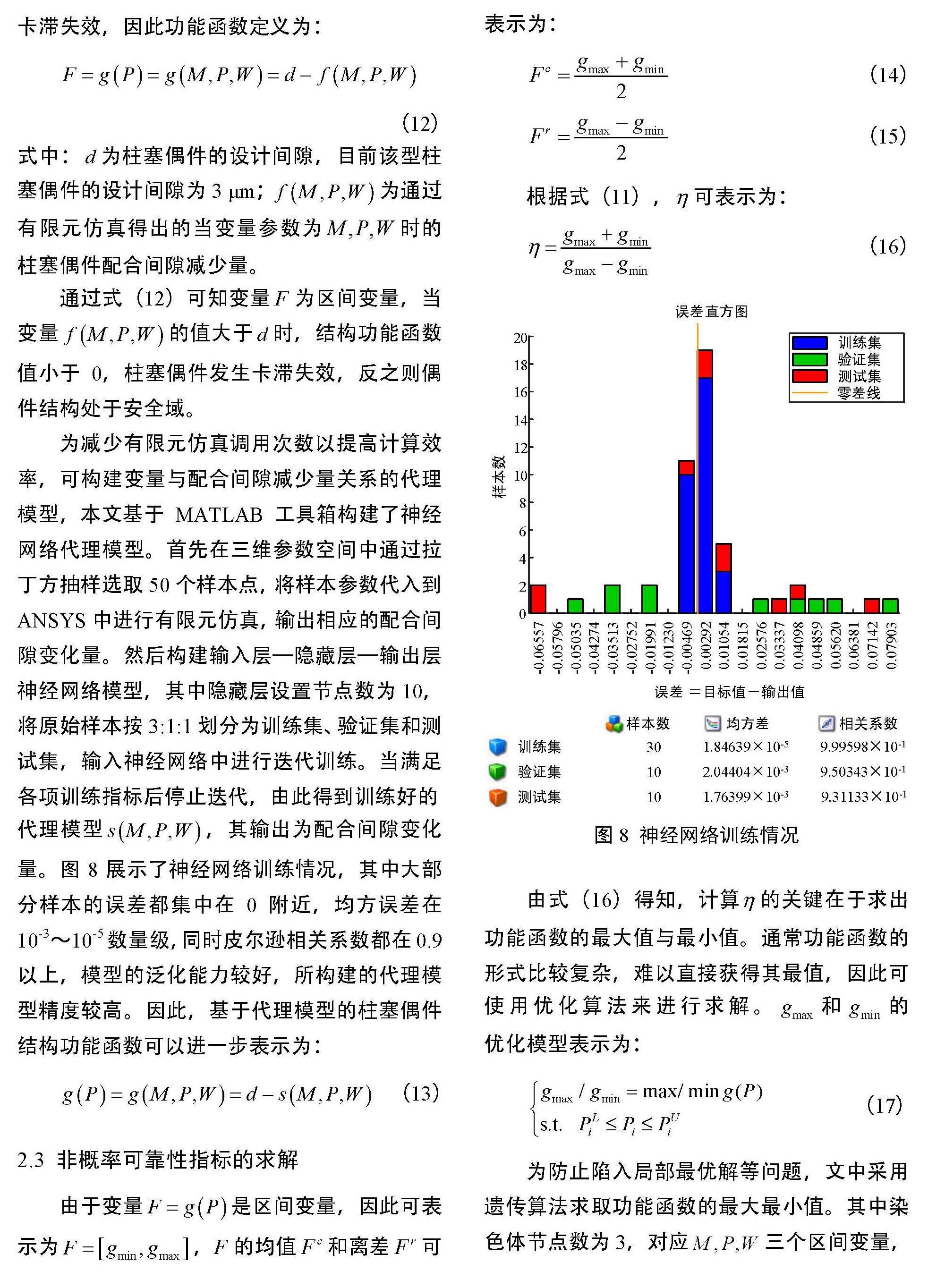
为减少有限元仿真调用次数以提高计算效率，可构建变量与配合间隙减少量关系的代理模型，本文基于MATLAB工具箱构建了神经网络代理模型。首先在三维参数空间中通过拉丁方抽样选取50个样本点，将样本参数代入到ANSYS中进行有限元仿真，输出相应的配合间隙变化量。然后构建输入层—隐藏层—输出层神经网络模型，其中隐藏层设置节点数为10，将原始样本按3：1：1划分为训练集、验证集和测试集，输入神经网络中进行迭代训练。当满足各项训练指标后停止迭代，由此得到训练好的

代理模型，其输出为配合间隙变化

量。图8展示了神经网络训练情况，其中大部分样本的误差都集中在0附近，均方误差在10-3～10-5数量级，同时皮尔逊相关系数都在0.9以上，模型的泛化能力较好，所构建的代理模型精度较高。因此，基于代理模型的柱塞偶件结构功能函数可以进一步表示为：

（13）

2.3 非概率可靠性指标的求解

由于变量是区间变量，因此可表示为，的均值和离差可表示为：

（14）

（15）

根据式（11），可表示为：

（16）

图8 神经网络训练情况

由式（16）得知，计算的关键在于求出

功能函数的最大值与最小值。通常功能函数的形式比较复杂，难以直接获得其最值，因此可

使用优化算法来进行求解。和的

优化模型表示为：

（17）

为防止陷入局部最优解等问题，文中采用遗传算法求取功能函数的最大最小值。其中染色体节点数为3，对应三个区间变量，

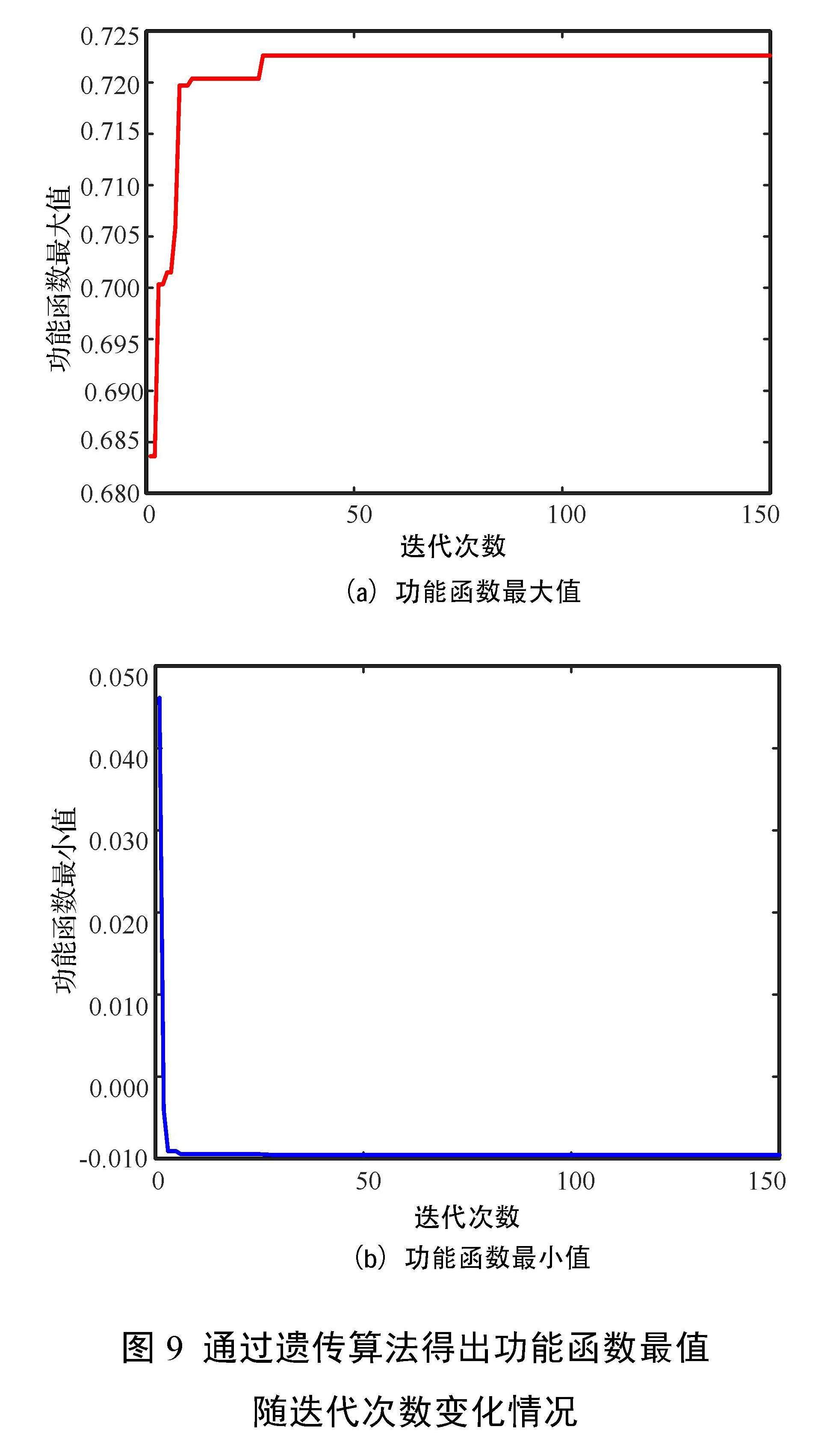
取值范围如表3所示；染色体适应度的计算由式（13）通过不断调用训练好的神经网络代理模型得到；设置每次迭代的种群数量为200，交叉及突变概率为0.2。经过150次迭代后得到最值变化情况如图9所示，此时功能函数最值已完全收敛。

通过迭代计算，得到功能函数最大值为0.72263，对应（M， P， W）＝（136.953， 60.022， 0.8）；功能函数最小值为-0.0095457，对应（M， P， W）＝（149.995， 98.197， 1.5）。根据式（16）计算

出该柱塞偶件的为0.97393。由于，目前

柱塞偶件的结构可能发生失效。

由上述研究可知，在工作载荷和不确定性的影响下，偶件结构会产生形变，导致其配合间隙发生变化。若配合间隙设计为3 μm，在工作载荷较大的条件下，偶件配合间隙减少量可能超出设计间隙，引起偶件结构失效。

为展示柱塞偶件设计间隙与η间的关系，通过数值模拟图10给出了设计间隙为3～4 μm时对应η的变化情况。研究表明两者呈线性关系，对应的拟合函数为：

（18）

式中：为非概率可靠性指标；为设计间隙。

据此，当设计间隙大于3.0094 μm时有

，偶件结构可靠。此外，文献[18]从平衡

润滑和泄露方面开展了相关分析，建议将配合间隙设置为3.5 μm，通过计算此时η为2.3391，因此，若配合间隙采用文献[18]的建议值，可保证偶件结构不发生失效的同时留有一定的安全余量。

3 结论

通过对柱塞偶件进行建模及结构仿真，研究得知偶件配合间隙在工作时易缩小，从而引发间隙不足导致卡滞。针对工程中数据量少和不确定性问题，文中采用区间分析方法构建了柱塞偶件结构非概率可靠性模型，利用神经网络对有限元仿真结果进行拟合并将其作为代理模型，然后采用遗传算法对代理模型的最优值进行求解，进而得出柱塞偶件结构非概率可靠性指标。

分析结果表明若采取原配合间隙设计方案3 μm，其非概率可靠性指标小于1，偶件结构可能会在载荷较大的情况下发生失效。如果采取文献[18]中建议的配合间隙设计值3.5 μm，能够将其非概率可靠性指标增大到2以上，该方案显著提升了柱塞偶件的结构可靠性，有利于避免偶件卡滞故障。

需指出的是，柱塞偶件的卡滞问题可能具有多种失效模式，比如因液相空化导致偶件表面材料剥落进入配合间隙引起卡滞等。后续可以针对如何有效抑制偶件空化展开流体仿真相关研究，除结构改进外，应能够从更换局部材料、覆盖DLC涂层以及改进制造工艺等方面入手，尽量减小流体层面造成的危害，提升柱塞偶件防卡滞可靠性。

参考文献：

[1]周惠琴. 柴油机柱塞偶件表面复合织构润滑与密封性能研究[D]. 镇江：江苏大学，2019.

[2]BEN-HAIM Y. A non-probabilistic measure of reliability of linear systems based on expansion of convex models[J]. Structural Safety，1995，17（2）：91-109.

[3]ELISHAKOFF I. Essay on uncertainties in elastic and viscoelastic structures： From A. M. Freudenthal's criticisms to modern convex modeling[J]. Computers and Structures，1995，56（6）：871-895.

[4]BEN-HAIM Y. A non-probabilistic concept of reliability[J]. Structural Safety，1994，14（4）：227-245.

[5]郭书祥，吕震宙，冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报，2001，18（1）：56-60.

[6]屠义强，王景全，江克斌. 基于区间分析的结构系统非概率可靠性分析[J]. 解放军理工大学学报（自然科学版），2003，4（2）：48-51.

[7]郭书祥，张陵，李颖. 结构非概率可靠性指标的求解方法[J]. 计算力学学报，2005，22（2）：227-231.

[8]宋利锋，陈振鸣. 非概率可靠性优化方法在机翼结构优化中的应用[J]. 机械制造，2022，60（8）：13-16.

[9]高泽民. 燃油杂质对柴油机可靠性和耐久性的影响[J]. 中国设备工程，2005（4）：55-56.

[10]彭琦，扈爽，雷友军，等. 某型喷油泵柱塞偶件失效分析[J]. 内燃机，2021（2）：26-28.

[11]赵晋. 高压共轨喷油器柱塞偶件密封特性研究[D]. 广州：华南理工大学，2018.

[12]司录荣. 轴向柱塞泵的有限元分析及壳体的优化设计[D]. 太原：中北大学，2014.

[13]张晋，黄橙橙，隋佳鑫，等. 超高压轴向柱塞泵缸体结构强度分析[J]. 液压与气动，2021，2：129-133.

[14]李治洪. 高压共轨喷油器精密偶件泄漏与密封特性研究[D]. 北京：北京交通大学，2019.

[15]王宏生，信幼平，苏长波. 高压共轨系统在135Ti柴油机上的配套设计及应用[J]. 机械设计，2011，28（12）：85-89.