一题一课：将思维引向深处

居素琴

1 一题一课的概述

所谓“一题一课”就是指教师深度研究一道试题或一个材料，充分挖掘或者拓宽其中隐含的学科本质，并引导学生在课堂教学过程中科学探究，以建构新知、生长能力、发展素养.“一题一课”是夯实“四基”及达成目标的有效教学方式，其最终目标是将学习者的思维引向深处，提升关键能力及发展数学核心素养.下面笔者以“正方形的性质”的教学为例，谈谈如何借助“一题一课”，将思维引向深处.

2 课前慎思

2.1 分析教材

本节课的知识基础是平行四边形、矩形及菱形.而实际教学过程中，我们常常发现在运用正方形性质解决实际问题时极易出错，唯有深度钻研教与学的方法，才能真正意义上将学生的思维引向深处，提升数学核心素养.“一题一课”教学方式的运用，可以在类比矩形、菱形的探究历程之后达成知识与方法的融会贯通；同时，在对正方形本身特殊性质的探索中掌握探究几何图形的一般路径，培养逻辑推理、类比迁移、直观想象、数学抽象等数学素养.

2.2 教学目标

（1）在设问、追问、质疑等一系列活动中理性认识正方形，切实理解其概念本质；

（2）探究正方形的性质，掌握运用正方形性质解决问题的方法，并在探究中培养逻辑推理、类比迁移等能力，提升数学素养.

2.3 教学片段再现

片段1：有效导入，引发思考.

问题1 回忆已学的平行四边形、矩形和菱形，三者共有的一个研究思路是什么？

追问：先分别说一说三者的概念，再说一说它们之间的特殊关系，最后想一想它们有何共同特点.

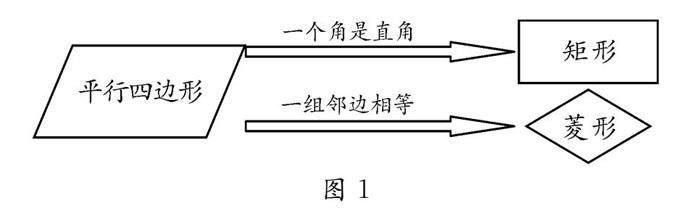
学生活动：学生在自主探究与合作讨论后清晰生成了共同研究思路，即“概念—性质—判定—应用”.后续对于教师的追问，学生思考并探究这些概念的异同点，剖析概念的条件和结论，切实厘清了三个概念之间的关系.在这个过程中，学生还形成了概念思维导图（如图1），让概念的关系得以动态呈现.

设计意图：教师从学生的已有知识经验着手，关注到当前学习内容的有机联系，尤其是注重从数学教学建立内在联系，而非牵强附会，让昨天的旧知为今天的所学服务，有效促进概念的快速建构.

片段2：巧妙设问，概念建构.

问题2 从图1中我们可以发现矩形与菱形均是特殊的平行四边形，且沿袭平行四边形的定义来定义了矩形与菱形.那么，这样的研究思路对正方形有何影响，如何让它成为更为特殊的平行四边形呢？

追问：正方形与前面探究的矩形和菱形有何特殊关系？请试着以多种方式描述正方形概念.

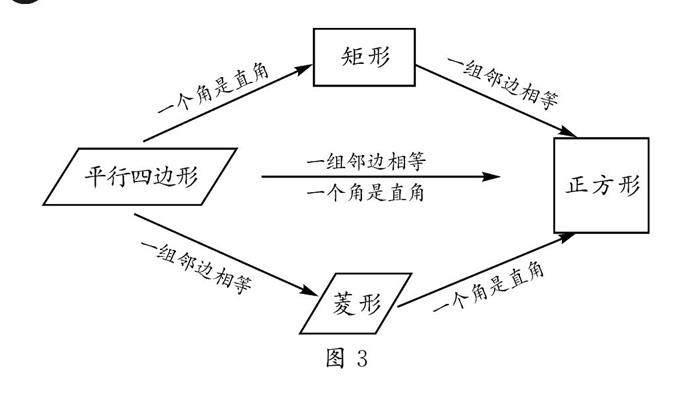
学生活动：问题2抛出后，学生很快展开了一系列类比探究活动，最终尝试组织语言进行表述，并在教师的点拨和启发下规范而完整地描述了正方形的概念，生成了概念思维导图（如图2），此处极好地培养和发展了抽象概括能力.

进一步的追问引发了学生的深度思考，学生自然而然地以三种形式描述正方形的概念，并收获了图3所示的概念思维导图，使得正方形的概念逐步清晰起来，为后续正方形判定方法的探究打下基础.

设计意图：学生在发现与解决问题的过程中，体会知识的探索，在冥思苦想中走向数学学习最兴奋的时刻.这里，正是因为教师为学生提供了一种探究氛围和学习机会，才使得他们大显身手，在独立探究、自主思考和主动参与中建构知识.

片段3：探索性质，思维生长.

问题3 在获悉概念后，下一步你打算从哪些方面研究正方形？

问题4 正方形的性质有哪些？你准备怎样研究？

追问：正方形还有什么性质？内部是否会出现特殊三角形？

设计意图：在这一环节，教师继续以问题＋追问促进学生思维的灵动生长.问题3则是引领学生在再回顾一般探究路径后，根据之前的经验直接将目标定位到对其性质的探究.问题4是需要学生基于矩形、菱形性质的研究经验，本着从一般到特殊的探究思路多角度、多方位地探究正方形的性质.进一步地，教师以追问促进数学思维的深化，让学生的思维自然生长.

片段4：解决问题，拓展认识.

问题5 如图4，已知动点E在正方形ABCD的对角线BD上，试着说一说在动点E的运动中线段AE，CE的数量关系.

变式1 将题设中的“对角线BD”改为“对角线BD所在的直线”，其余不变.

变式2 如图5，若动点E在边BC的反向延长线上运动至点E1，使BE1=BD，连接DE1，试求∠E1的度数.

变式3 将变式2中的“边BC的反向延长线”改为“边BC的延长线”，其余不变.

变式4 如图6，已知正方形ABCD的对角线BD上有两点E，F，且BE=DF，连接AE，AF，CE，CF，试猜测四边形AECF的形状，并予以验证.

变式5 如图7，将变式4中的“对角线BD”改为“对角线BD的延长线”，其余不变.

延伸1：问题5中的题设不变，试求点E运动至何处，该正方形内部有两个等腰三角形？

延伸2：已知正方形ABCD，能否在其内部找到一点E，在连接点E及各顶点后将该正方形分割为4个等腰三角形？若能，请作图说明共有几个这样的点E；若不能，请阐明原因.

延伸3：将延伸2中的“内部”改成“外部”，其余不变.

设计意图：从问题到变式旨在发散思维，在延伸拓展中培养高阶思维能力.进一步地，教师以开放性的拓展题拾级而上地促使学生经历观察、探索、作图、验证等探究活动，获得思维的进阶.

片段5：课堂小结，概括深化.（略）

3 一题一课的教学反思

3.1 类比思维是激活数学思考、优化知识结构的内在活力

基于定义去构建研究几何图形性质的基本思路，可以引领学生层层递进地有序研究.问题引领，学生思想上产生的自觉的类比思维才是激活数学思考、优化知识结构的内在活力.在本课中，正方形的定义是类比矩形和菱形得到的，正方形的性质亦是如此.就这样，学生在类比思维中砥砺前行，积极主动地建构和生成，极好地孕育了数学核心素养.

3.2 一题一课是刺激思维进阶、提升核心素养的不竭动力

变式是“一题一课”中的重要一环.精选好题进行变式训练，不仅可以促进知识的巩固与整合，还能促进完整认知体系的建构，更重要的是刺激思维的进阶，提升学生的数学核心素养.本课以动点问题为例进行变式，促进了正方形性质的巩固，并指引学生发现了“变中的不变”.之后的延伸题则引领学生获得数学探究的必要能力与方法，极好地发展了几何直观、数学推理等关键能力.

总之，想要将学生的思维引向深处，让学生的数学学习更有思维，需要顺应学生的思维，从一题一课展开，引导学生深度探究.在这个过程中，学生不仅能习得知识，发展主动探究的意识和精神，还能实现学力的生长，发展数学核心素养.