关注概念生成，培养数学素养

杜莹

1 问题提出

章建跃博士指出，数学核心概念的理解对数学素养的提高有关键作用，能从与核心概念的联系作出具体分析，并给出不同角度解释概念的具体例子是数学素养高的具体表现.因此，要发展数学能力需要着重指导学生对数学核心问题的探索与对数学核心概念的理解.

数学概念是数学思想的凝结，数学思想是数学概念的升化.数学概念的教学通常要经历观察与实验、联想与类比、比较与分类、抽象与概括、记忆与应用等阶段.函数作为数学的核心概念，其教学意义非同一般，笔者以一节“函数”概念研讨课的教学设计为例展开论述“注重概念生成，培养学生数学素养”的具体做法.

2 教学设计

2.1 创设情境，提出问题

观看短视频，揭示万物皆变，变化过程中往往蕴含着量的变化，把握了变量之间的关系就能掌握变化规律.

设计意图：通过大自然中的实例，学生能够感受到万物皆变.利用2020年新冠疫情每天新增确诊人数的短片勾起学生的回忆，引导学生关注数据的变化.通过社会热点及每位学生感同身受的生活实例，复习“变量”的内容，提出本节课要学习的内容，引起合理的注意.

2.2 观察思考，分析变化

问题1 在以下变化过程中，各有几个变量？

（1）全国同胞捐赠医疗急需物资驰援武汉，货车以60 km/h的速度匀速行驶，行驶时间为t h，行驶距离为s km.

（2）每包口罩售价为20元，某口罩制造商每天售出x包，该日销售收入为y元.

（3）水中涟漪，圆形水波慢慢扩大，圆的半径为r，面积为S.

（4）用10 m长的绳子围一个矩形，矩形的一边长为x m，另一边长为y m.

追问：你能用其中一个变量表示另一个变量吗？

2.3 观察思考，分析归纳

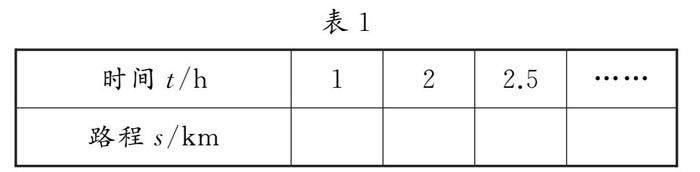
追问：在（1）这个变化过程中，s是怎样随着t的具体变化而变化的呢？完成表1，用数值加以说明.

师生活动：教师引导学生取定t的一些值，计算s的对应值，通过动画展示，并填写表格.引导学生对变化过程（2）（3）（4）作出类似于变化（1）的变量关系分析，小组展示，并总结表述.

问题2 请用自己的语言说说这些变化过程中变量之间关系的共同特征.

2.4 观察思考，再次归纳

问题3 在我国人口数统计表（PPT呈现）中，人口数随着年份的变化而变化，这个变化过程符合刚才总结的共同特征吗？

问题4 2020年初我国新冠新增确诊统计图中，新增确诊人数随着日期的变化而变化，这个变化过程符合刚才总结的共同特征吗？

问题5 上述实际问题中，有两个变量，当一个变量确定后，可以通过关系式、表格、图象确定另一个变量唯一的值.你能归纳出它们的共同特点吗？请大家相互讨论.

师生活动：学生分组讨论，归纳出如下共同特征——（1）在一个变化过程中；（2）有两个变量；（3）当一个变量取定一个值时，另一个变量有唯一确定的值与之对应.最后，整理出函数的概念.

追问：其实函数就是变量间的一种对应关系，那么s=120、人口数为13.71亿、新增确诊人数为14 109例是什么含义？

师生活动：学生发言，生生互评，并顺势得出函数值的概念.

问题6 比较问题1、问题3与问题4，在一个变化过程中获取函数值的方式有哪些？

师生活动：学生观察思考，总结函数的不同表现形式.

观看视频，了解函数的发展史.

问题7 请用函数的定义阐释问题1中的4个变化过程.

2.5 初步应用，巩固知识

练习1 下列式子中的y是x的函数吗？说明理由.

（1）y=3x－5；

（2）y=x－2x－1；

（3）y=x－1；

（4）|y|=x.

练习2 调出今天早上7时至下午4时的气温变化图，气温是时间的函数吗？

练习3 图1各曲线中哪些表示y是x的函数？

练习4 请举一个函数的实例.

2.6 小结

（1）请说说函数的概念和表示方法；

（2）从数学思想方法角度，说说本节课你的收获.

2.7 布置作业

课本习题19.1第1～5题；举一个函数的实例.

3 教学感悟

3.1 精心创设情境，提高观察能力

数学概念不是凭空想象出来的，它来源于生活，脱胎于实际需要，抽象化而得来，比如函数，也有一些数学概念是从既有的数学概念衍生或发展而来.由此可见，数学概念和生活密切相关，教师精心创设问题情境，可以让学生通过现实的例子初步形成感性认识.

本节课情境导入设计的4个变化过程，具有以下三个特点：（1）时效性的情境让课堂一开始便具有代入感，也是家国情怀的无声渗透，体现数学教学的德育作用；（2）贴近生活、简单具体的问题，问题来源于生活实际，运算简便，便于学生观察、思考和计算，节省计算和思考的时间，充分提高课堂效率；（3）形式多样化，

有行程问题、销售问题、面积和周长问题，也有正比例函数、二次函数和一次函数的实例.多样的实例可以凸显函数概念的本质特征，淡化非本质特征.

创设好问题情境，为学生的学奠定基础，让学生在具体的实例中观察，发现问题，形成认识.观察能力是科学探究与发现的基本能力，巴甫洛夫曾将“观察，观察，再观察”写在实验大楼正面.所以，在进行数学概念教学时，教师要精心设计情境，为学生观察提供有效基础，为学生观察能力的提升创造契机.

3.2 体验与反思并行，提升思维能力

数学概念的形成和发展不是一蹴而就的，是一个动态过程，数学思想在这些探索与发现过程中熠熠生辉，正是数学魅力之所在，所以教师在组织概念教学时不可和盘托出，应根据教学需要有选择地还原其发展历史，让学生体验知识的形成过程，从中体会数学思想.函数发展在300年的时间长河中，经过多位数学家的不懈探索和反思逐渐发展完善.函数概念从依赖到对应，由图象到表达式，表达形式逐步广泛和丰富，其发展与完善的过程在课堂教学中再现，让学生更深刻地理解函数概念的内涵和本质.

通过视频整体把握函数发展历史，引领学生经历概念的发生发展过程，帮助学生深刻理解概念，形成知识架构，培养严谨生动、广泛深刻的思维品质.

3.3 优化问题设计，提升概括能力

该教学设计中有多个问题与追问，问题具体、有梯度，给学生的观察与思考指明方向，体现学生主体地位和教师主导作用.函数是一个非常抽象的概念，遵循人的认知规律，教师有必要提供大量具体的实例让学生观察，归纳概括它们的共同点即本质特征，才能较为准确地获得函数的概念.因此，教师提问要明确、有层次，逐级深入，才能引导学生的思维逐步深入概念的内核，准确把握知识内涵，这个过程也是锻炼学生抽象概括能力的好时机.

3.4 注重概念应用，培养应用能力

数学概念的学习具有二重性的特征，概念的形成是由特殊到一般，其运用则表现为从一般到特殊.学生若能准确应用概念则一定是理解了该定义，因此应用练习是检验课堂教学效果的标准之一.本“函数”教学设计的一大亮点在于让学生举函数实例，并表述分享.学生的回答有：每日测温表，某位学生每日午测的体温是时间的函数；物理书中的物体熔化的温度随时间变化的图象，物体的温度是时间的函数；地理课本中平均降水量随纬度变化的图象，平均降水量是纬度的函数；等腰三角形顶角为α，底角为180°-α2，底角是顶角的函数.学生列举的都是身边或已有知识的例子，还有多学科融合.学生不禁总结道“生活处处皆函数”，也充分感受到数学广泛的应用价值.学生列举的这些实例形式多样，有表格、图象和解析式，表述准确，实现了理解函数概念的目标，并发展了学生应用知识和迁移运用的能力.

常言道：“温故而知新”，“学以致用”.进行数学概念教学时，适当的巩固练习、辨析运用和设计的开放性问题，是对学生学习情况的摸底，也是对教学效果的检测，更是让课堂教学在各个环节实现教学目的，深化概念理解，使思维更具灵活性和广泛性，培养迁移和应用数学知识的能力.