“教-学-评”一体化学习进程设计与实施
2024-06-21李雪莱
李雪莱

学习进程指学生达成学习目标需要经历的学习过程。学习进程设计可以指向整个学段教学过程的规划,可以指向整个单元教学主题活动的规划,还可以指向某个课时教学环节的规划。本文以《摆一摆,想一想》数学综合实践活动课为例,探究“教-学-评”一体化的学习进程设计与实施。
一、明晰教学目标
《摆一摆,想一想》是综合与实践学习领域的内容,旨在引导学生通过把一定数量的圆片分别摆在数位表的十位和个位上,得到不同的数的活动过程,进一步巩固100以内数的认识,体悟“位值制”思想。一年级学生刚接触100以内的数,认识了数位顺序和数的组成,有较好的知识基础与学习经验。但学生处在初步体验位值制思想的阶段,有序思考能力不强,在摆一摆的过程中会出现遗漏的情况;缺少数学基本活动经验,不能准确表达和记录活动结果;自主探究规律的意识不强。这些是本节课教学要面临的困难。
课程标准明确指出,综合与实践主题活动的目标表述应该向学生传达清楚具体的活动要求,便于学生明确所要完成的任务及任务涉及的各方面指标,进而在清晰的目标下制订方案,开展解决问题的系列活动。
综合《摆一摆,想一想》的课程目标、学段目标和单元目标,笔者确定了“①通过在数位表上摆圆片的活动,加深对100以内数的认识,进一步巩固数位和位值的概念;②通过探究圆片个数与所摆出的数的个数之间的关系,学会发现规律;③能用发现的规律解决一些简单的实际问题,培养初步的归纳能力;④在自主探索中体会有序思考的重要性,在合作交流中养成倾听、有条理地表达想法的习惯和意识,体会数学与现实生活的联系”的课时教学目标,并明确了“在活动中巩固数位和位值思想,加深对100以内数的认识”的教学重点和“在活动中感受有序思考的价值,初步培养归纳能力、形象思维能力和抽象思维能力”的教学难点。
二、匹配评价方案
笔者将教学目标与表现性评价任务、终结性评价水平划分相匹配,明确评价方案。例如,教学目标①对应的表现性评价目标是“学生在摆圆片的活动中,小组交流合作,根据自己摆的结果完成简单表格的记录”,相应的终结性评价水平处于理解层次。教学目标④对应的表现性评价目标是“学生经历完整的发现、提出、分析、解决问题的过程,并能将有序思考的数学思想应用到其他数学问题中”,相应的终结性评价水平处于体验、应用层次。
在学习进程的设计与实施过程中,评价伴随始终,在活动过程中,教师要进行多维、多元、多样化的评价:活动过程评价与学习成果评价并重,自评与互评并行,操作表现的评价和倾听表现的评价并举。
三、设计学习活动
专题学习活动1:玩中生成问题
对一年级学生来说,感受数学的乐趣非常重要,因此,笔者设计了“摸圆片,比大小”的游戏,让学生在游戏中产生“同样多的圆片怎样摆出不同的数”的疑问,从而复习了数位与位值的概念。学生发现同一个圆片摆在不同的数位上表示的数不同,并且理解了数位表的用途。
专题学习活动2:摆中引发思考
笔者引导学生尝试用圆片在数位表上摆出不同的数,把结果记录在简单的统计表中,进行有序思考。
第一次,尝试摆,运用知识。学生在笔者指导下用数位和数值的知识摆出2个圆片的所有组数情况,并将结果完整记录在表格内。
第二次,探究摆,展示发现。学生通过用3个圆片摆出并读出不同的数,发现可以通过思考数的组成,不重复、不遗漏地摆出所有答案,便于按顺序记录结果。小组内学生在逐个移动圆片的过程中初步体会了有序思考,认识到摆数可以从大到小摆,也可以从小到大摆。
第三次,运用摆,感悟规律。借助第二次摆发现的窍门,学生用4个、5个圆片分别摆出不同的数,有的学生甚至能直接记录摆的结果。通过静心观察,学生发现、总结其中蕴含的规律:摆出的不同的数的个数比圆片的个数多1。
第四次,不用摆,迁移规律。最后,学生不必摆圆片,就综合运用所发现的规律,直接说出用6,7,8,9个圆片能摆出哪些数。
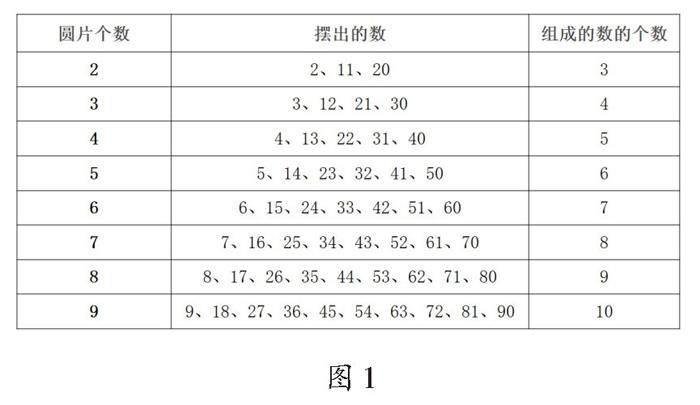
活动过程中,学生从依托学具操作到逐步摆脱学具,他们在观察、比较、分析中习得了学习方法,提升了抽象思维水平,得到了数学规律:把一定数量的圆片分别摆在数位表的十位和个位上,组成的数的个数比圆片的个数多1(如图1所示)。
专题学习活动3:辨中积累经验
笔者通过教材中的形象小机器人聪聪设置闯关游戏情境,让学生在学中玩,在玩中学,积极主动地运用规律解决问题。
闯关1:由形到数验证规律。“小芳用6个圆片摆出了下面这些数,你们读一读,想一想,说一说,她摆得对吗?你们有什么发现?”学生发现6个圆片应该摆出7个数字,小芳只摆出了6个数字(60,51, 42, 24, 15, 6),还差数字33。
闯关2:由数到形应用规律。“老师给大家一些数,8,17,26,35,44,53,62,71,80,你们知道这些数是通过摆几个圆片表示出来的吗?你们是怎么知道的?”学生发现9个数字,需要8个圆片才能摆出来,并进行了操作验证。
闯关3:数形结合拓展规律。笔者出示□、□、□、□、□、□、□、□,并引导:“现在一个数都不提供,用一个□表示一个数,那么方框中的这些数是用几个圆片表示出来的?其中最大的数是多少?最小的数是多少?”学生发现这些数是用7个圆片表示出来的,最大的数是70,最小的数是7,并得出规律:用了几个圆片,最大的数就是几十,最小的数就是几。
专题学习活动4:联中拓展能力
在本节课的最后,笔者出示百数表,使教学重新回到数的组成与认识中。笔者引导学生思考:当圆片的个数继续增多时,所摆出来的数还有这样的规律吗?10个圆片是什么情况?11个、12个圆片呢?请你结合记录表和百数表(如图2所示)思考。
学生通过摆圆片以及观察百数表,发现圆片数量超过10个时,规律已经不同。以10个圆片为例,会出现个位上或十位上摆10个圆片的情况,这样的数是摆不出来也读不出来的,因为个位和十位上的数都必须小于10。斜着看百数表,学生发现能得到所有“个位和十位上数字相加之和是10”的两位数,这才是可以用10个圆片摆出的数。这一学习活动沟通了百数表与所摆出的数之间的关系,让学生直观理解了100以内数的特点。
(作者单位:武汉市汉阳区墨水湖小学)
(本文为“教-学-评”一体化主题征文获奖作品)
责任编辑 孙爱蓉
