基于有限元模拟材料缺陷对U71Mn钢表面主裂纹的影响
2024-06-14王强胜江晓禹
王强胜 江晓禹

收稿日期:2023-03-28
基金项目:国家自然科学基金(11472230)
作者简介:王强胜(1992—),男,硕士,从事材料断裂行为研究.Email:qs18582599601@163.com
通信作者:江晓禹(1965—),男,博士,教授,从事复合材料力学和接触疲劳研究.Email:xiaoyujiang8@sina.com
摘要:通过有限元法研究了U71Mn钢在弹塑性状态下,其材料缺陷(孔洞)对表面主裂纹尖端力学行为的影响.重点分析了裂纹尖端张开位移(CTOD)、表面张开位移(FSOD)、孔洞方位角β与孔洞半径r等相关变量对裂纹尖端J积分的影响.结果显示,裂纹面对应力有屏蔽作用,导致裂纹面附近的应力松弛,而裂纹尖端对应力有放大作用,随着外力增加将导致裂纹的扩展;孔洞位于主裂纹尖端约-75°<β<75°范围时,孔洞将促进裂纹尖端的变形,导致CTOD及J积分值增加,促进主裂纹的扩展;而孔洞位于75°<β<90°或-90°<β<-75°范围时,孔洞将阻碍裂纹尖端的变形,导致CTOD及J积分值均比无孔洞时要小,从而抑制主裂纹的扩展.
关键词:U71Mn钢;孔洞;J积分;裂纹张开位移;裂纹扩展
中图分类号:TG142;TB115
文献标志码:A
0引言
在材料的加工制造和应用过程中不可避免地会有缺陷产生,比如孔洞、杂质与裂纹等[1].缺陷将对材料的疲劳和断裂行为产生较大的影响,主裂纹尖端附近的缺陷对裂纹的扩展速率和扩展方向有着很大的影响[2].为此,缺陷和裂纹的相互作用成为科研人员的重点研究方向.段士杰等[3]通过复变函数方法得到了无限大弹性平面内含圆孔问题的理论解.Dundurs[4]、Wang[5]和Wang等[6]对基体中含有1个圆形杂质和刃型位错的相互作用问题进行了相关研究.文献[7-8]利用分布位错技术研究了复杂载荷作用下半无限大平面内表面裂纹问题,并通过数值方法得到了该问题的数值解.Tao等[9]利用分布位错技术研究了远场载荷作用下,平面内含有1条裂纹、1个刃型位错和1个夹杂的相互作用问题.Zhang[10]、Tamate[11]和Erdogan等[12]研究了平面内含1条裂纹和1个圆形杂质的相互作用问题.樊礼赫等[13]基于分子动力学方法研究了含孔洞的双晶TiAl 合金试样在单轴拉伸作用下材料变形和断裂过程中的缺陷演化行为.
上述文献及其他研究者中大多数是基于线弹性断裂力学,用理论推导或数值模拟等方法研究材料部分缺陷与裂纹之间的相互作用.由于弹塑性模型的复杂性及相关理论的不完善,目前,较少有学者在考虑符合材料实际属性的弹塑性模型基础上,开展对材料缺陷与裂纹之间相互影响问题的研究.因此,本研究以铁路常用的U71Mn钢材为研究载体,选用符合钢材属性的弹塑性本构模型,基于有限元软件ABAQUS建立计算模型,以此研究了U71Mn钢在弹塑性状态下,其材料缺陷(孔洞)对表面裂纹尖端力学行为的影响,得到了一些能有效表征裂纹扩展及材料破坏的力学参量,从而为U71Mn钢材料的断裂破坏和实际工程应用提供理论依据.
1研究模型
基于实际材料中不可避免地存在各种缺陷,本研究将重点研究U71Mn钢中孔洞缺陷对其表面裂纹尖端力学行为的影响.图1为理论研究模型,在平面中预设1条长度为2a的表面直裂纹及1个处于任意位置,半径为r的圆形孔洞,孔洞中心距裂纹尖端的距离为d,与水平方向的夹角为β,定义β逆时针方向为正,平面长和宽几何尺寸分别为L和H,为降低边界对裂纹的影响效应,取L<H,并在L两端施加均匀拉伸载荷σ∞.
2有限元计算
2.1本构模型与材料参数
2.1.1本构模型
U71Mn钢因其具有良好的韧性和塑性被广泛应用.本研究采用各向同性硬化—弹塑性本构模型进行有限元结果的模拟,并在ABAQUS中,按照“Mechanical → Plasticity → Plastic:Hardening:Isotropic”方式输入模型材料参数.该模型中,应变的每一增量(dε)将由弹性可逆变形(dεe)与塑性不可逆变形(dεp)叠加组成,计算公式为,
dε=dεe+dεp(1)
2.1.2材料参数
本研究采用U71Mn钢材,其基本材料参数见表1,根据ABAQUS中各向同性硬化—弹塑性本构模型材料参数输入要求,依次输入塑性材料参数应力(σ)和相对应的塑性应变(εp)值,结果见表2.
由表2应力—应变实验数据值,得到了图2所示的应力(σ)—总应变(εe+εp)曲线及应力(σ)—弹性应变(εe)线,应力随总应变的曲线变化及随弹性应变的线性变化特征符合U71Mn钢材料属性.
2.2有限元模型
本研究在既能保证单元数量,节约计算成本,又能满足精度要求的前提下,选取模型几何尺寸为L×H=20 mm×30 mm,通过ABAQUS建立了二维弹塑性有限元模型,如图3所示.其中,图3(A)为整体有限元模型,在其表面预设了初始长度2a=2 mm的主裂纹及在裂纹尖端区域设置了任意方位的孔洞缺陷.本研究采用平面应力状态计算,选取CPS4R双线性四节点单元,整体单元网格尺寸为06 mm,裂纹尖端及孔洞附近细化尺寸到0.02 mm,全模型单元总数达到5 734个,图3(B)为裂纹及孔洞区域有限元模型局部放大图.
3结果验证
各向同性材料在线弹性静态断裂问题中,反应裂纹尖端区域能量的J积分与其裂纹尖端应力强度因子之间的关系[16]为,
J=1ν2E(K2I+K2II)+K2III2G(2)
式中,E为弹性模量,G为剪切模量,ν为泊松比.对于平面问题则为,
J=1E(K21+K2II)平面应力问题
1-v2E(K21+K2II)平面应变问题(3)
为了降低有限元网格尺寸对计算结果的影响及验证有限元结果的正确性.本研究计算了图1模型在线弹性状态下受远场均匀拉伸载荷σ∞=50 MPa时的应力强度因子,进而由公式(3)得到了相应J积分的计算值,并将该计算值与ABAQUS中通过围线积分法得到的J积分模拟值进行对比,结果见表3.
从表3可以看出,当单元网格达到一定尺寸后,其对计算结果的影响较小.从J积分的计算值与有限元的模拟值对比发现,2项数值大小几乎相等,最大误差仅为0.12%;同时,采用已有的实验观察现象来验证本研究结果的正确性.综合以上讨论,得出本研究通过ABAQUS划分的单元网格尺寸及计算结果是可靠的,故本研究后续结果计算将依托ABAQUS进行.
4结果与分析
4.1结果云图
对于含裂纹的材料,其裂纹尖端是应力最集中,也是最危险的区域.为了更加直观地看到表面主裂纹附近应力与应变场的分布情况,计算得到了裂纹尖端区域等效应力(Von Mises)与等效塑性应变(PEEQ)云图,如图4所示.计算参数取d=1 mm,r=0.1 mm,β=0°,σ∞=200 MPa.
从图4(A)Von Mises应力云图中可以看到,裂纹面顶部和底部区域的应力远小于外加载荷σ∞,而裂纹尖端区域的应力大于σ∞,说明裂纹面对应力有屏蔽作用,导致裂纹面附近区域的应力松弛,而裂纹尖端区域对应力有放大作用.因此,在裂纹尖端附近发生应力集中,随着外力增加将促进裂纹的扩展.图4(B)为等效塑性应变云图,其变化形式与应力相似,裂纹尖端区域发生的塑性应变最大.
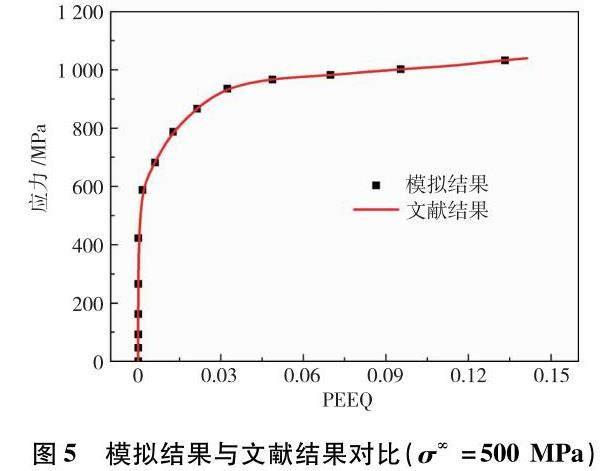
图5为提取裂纹尖端某单元的应力与等效塑性应变数据,并与U71Mn钢单拉应力—应变实验数据做对比发现,两者完全吻合,再次验证了本研究模拟结果的正确性.
4.2张开位移
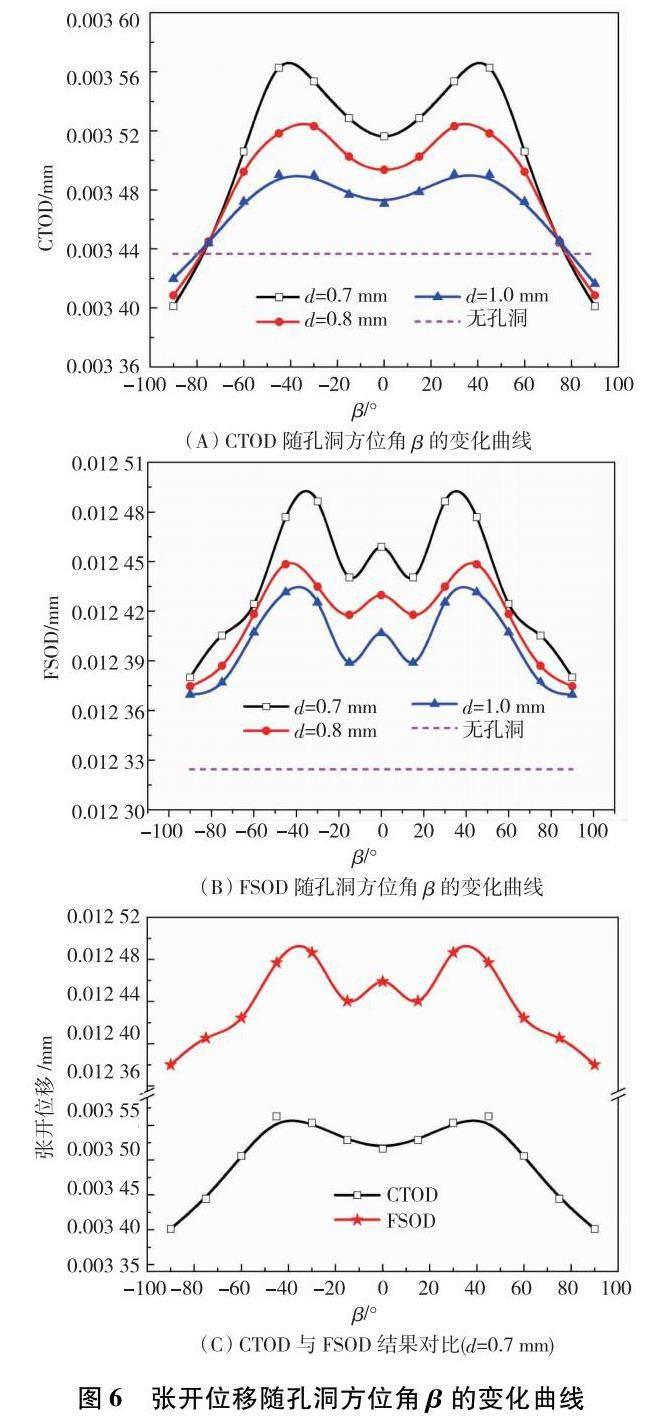
对于弹塑性表面裂纹问题而言,裂纹尖端张开位移(CTOD)和表面张开位移(FSOD)同样能有效表征材料在外载荷作用下的变形情况及失效行为.图6为张开位移随孔洞方位角β的变化曲线,计算参数取r=0.1 mm,σ∞=200 MP.
从图6(A)CTOD随β的变化曲线可以看出,孔洞位于主裂纹尖端约-75°<β<75°范围时(该位置为裂纹尖端区域),孔洞将促进裂纹尖端的变形,导致CTOD值均比无孔洞时要大,且随着孔洞距裂纹尖端越近(d越小),CTOD值越大,当孔洞位于β=±45°附近时,CTOD值达到最大值;而孔洞位于-90°<β<-75°或75°<β<90°范围时(该位置为裂纹面底部或顶部区域),孔洞将阻碍裂纹尖端的变形,导致CTOD值比无孔洞时要小.图6(B)中,FSOD随β的变化规律与CTOD变化规律基本相似,区别在于有无孔洞将对FSOD数值有较大的影响及孔洞位于-15°<β<15°范围时,FSOD随着β发生小幅度的增加后减小,在β=0°时FSOD达到第二个极大值点.图6(C)为CTOD与FSOD的结果对比,两者变化趋势相近,但FSOD数值大小约为CTOD的3.6倍,与实际观察现象相吻合.
4.3孔洞方位角β对J积分的影响
在弹塑性断裂力学中,J积分可以有效表征裂纹尖端的弹塑性应力与应变场.当裂纹尖端的应力与应变场达到裂纹开始扩展的临界状态时,J积分也达到临界值JC,弹塑性状态下裂纹的开裂判据[17-18]为,
J≥JC(4)
式中,JC是跟材料属性有关的参数,可由实验测得.
图7为J积分随孔洞方位角β的变化曲线,计算参数取r=0.1 mm,σ∞=200 MP.
从图7中看到,J积分随孔洞方位角β变化趋势与CTOD变化曲线相近.同样,孔洞位于裂纹尖端区域,即在-75°<β<75°范围时,孔洞的存在将使主裂纹尖端J积分值增加,促进主裂纹的扩展,孔洞离裂纹尖端越近,对J积分的影响越大;而当孔洞位于裂纹面顶部或底部区域,即在75°<β<90°或-90°<β<-75°范围时,孔洞将使主裂纹尖端J积分值减小,从而抑制主裂纹的扩展.该结论可从图4(A)中得到进一步的解释说明.
4.4孔洞尺寸对J积分的影响
孔洞的存在将在其附近区域产生应力集中,进而改变裂纹尖端区域的应力与应变场.为此,本研究计算了孔洞尺寸大小对裂纹尖端区域J积分的影响,如图8所示.计算参数取d=1 mm,β=0°.
从图8可知,主裂纹尖端区域J积分随孔洞半径r的增加呈非线性趋势增加,说明孔洞越大,造成主裂纹尖端区域应力场越强,越容易导致裂纹的扩展;外加载荷越大,使得J积分值越大,裂纹越容易扩展.
5结论
本研究通过有限元分析方法研究了U71Mn钢在弹塑性状态下,其材料缺陷(孔洞)对表面裂纹尖端力学行为的影响,得到了以下结论:
1)裂纹面对应力有屏蔽作用,导致裂纹面附近的应力松弛;裂纹尖端对应力有放大作用,随着外力增加将促进裂纹的扩展.
2)孔洞位于主裂纹尖端约-75°<β<75°范围时,孔洞将促进裂纹尖端的变形,导致CTOD及J积分值增加,促进主裂纹的扩展;而孔洞位于75°<β<90°或-90°<β<-75°范围时,孔洞将阻碍裂纹尖端的变形,导致CTOD及J积分值均比无孔洞时要小,从而抑制主裂纹的扩展.
3)同等条件下,FSOD数值大小约为CTOD的3.6倍.
4)孔洞离裂纹尖端越近,对J积分的影响越大,越容易发生裂纹扩展.
5)主裂纹尖端J积分值随孔洞半径r的增加而呈非线性趋势增加,孔洞越大,越容易发生裂纹的扩展.
参考文献:
[1]范天佑.断裂理论基础[M].北京:科学出版社,2003.
[2]邢帅兵,王强胜,生月,等.圆形杂质对裂纹扩展的影响[J].应用数学和力学,2019,40(2):189-199.
[3]段士杰,刘淑红.剪切荷载作用下圆孔孔边裂纹的解[J].应用数学和力学,2016,37(7):740-747.
[4]Dundurs J,Mura T.Interaction between an edge dislocation and a circular inclusion[J].J Mech Phys Solids,1964,12(3):177-189.
[5]Wang X,Schiavone P.Interaction between an edge dislocation and a circular inhomogeneity with a mixedtype imperfect interface[J].Arch Appl Mech,2017,87(1):87-98.
[6]Wang C C,Zhao Y X,Zhang Y B,et al.The interaction between an edge dislocation and a semiinfinite long crack penetrating a circular inhomogeneity[J].Theor Appl Fract Mech,2015,76:91-99.
[7]王强胜,李孝滔,昝晓东,等.分布位错法研究移动赫兹压力作用下次表面裂纹的力学行为[J].表面技术,2019,48(6):252-260.
[8]王强胜,李孝滔,昝晓东,等.分布位错法研究钢轨表面边缘直裂纹的力学行为[J].表面技术,2020,49(2):200-211.
[9]Tao Y S,Fang Q H,Zeng X,et al.Influence of dislocation on interaction between a crack and a circular inhomogeneity[J].Int J Mech Sci,2014,80:47-53.
[10]Zhang J,Qu Z,Huang Q,et al.Interaction between cracks and a circular inclusion in a finite plate with the distributed dislocation method[J].Arch Appl Mech,2013,83:861-873.
[11]Tamate O.The effect of a circular inclusion on the stresses around a line crack in a sheet under tension[J].Int J Fract Mech,1968,4:257-266.
[12]Erdogan F,Gupta G D,Ratwani M.Interaction between a circular inclusion and an arbitrarily oriented crack[J].J Appl Mech,1974,41(4):1007-1013.
[13]樊礼赫,冯瑞成,姚永军,等.孔洞对双晶TiAl合金断裂行为影响的声发射响应[J].稀有金属材料与工程,2022,51(8):2923-2932.
[14]文良华,李孝滔,江晓禹,等.考虑次裂纹时U71Mn钢的主裂纹扩展行为[J].机械工程材料,2017,41(6):79-83.
[15]田越,程育仁.U71Mn轨钢拉伸应力应变曲线的RambergOsgood模型拟合[J].物理测试,1991,9(5):30-35.
[16]Chambel P,Martins R F,Reis L.Fatigue crack growth under Mode I,II and III for planestrain and planestress conditions[J].Proc Eng,2014,74:232-235.
[17]王自强,陈少华.高等断裂力学[M].北京:科学出版社,2009.
[18]程靳,赵树山.断裂力学[M].北京:科学出版社,2006.
(责任编辑:伍利华)
