508-Ⅲ坯料锻造过程孔洞变化规律的数值模拟

2023-11-24李胤宪胡杰蒋燕超杨志洪

金属加工(热加工) 2023年11期

李胤宪，胡杰，蒋燕超，杨志洪

1.天津重型装备工程研究有限公司天津 300457

2.东北大学材料电磁过程研究教育部重点实验室辽宁沈阳 110167

1 序言

随着经济的发展，人们对能源的需求越来越大，传统的能源日渐枯竭，而核电作为一种高效清洁能源，受到各国青睐。核电压力容器是核反应堆的重要部件，需要在高温、高压、高辐射的环境中稳定工作，对核安全起着至关重要的保障作用。目前，国际上大都采用508-Ⅲ钢制造核电压力容器，生产流程一般需要冶炼、锻造、热处理等。然而，大型钢锭的冶炼工艺流程决定了坯料内部可能出现孔洞缺陷，对核电压力容器的综合性能产生严重的影响[1-3]。因此，在锻造过程中消除孔洞缺陷，对锻件的质量尤为重要。

由于大型锻件重量和尺寸较大，因此制约了大型孔洞闭合的可操作性，近些年来，随着科学技术的发展，计算机性能和功能有了很大的提升，数值模拟方法为大型锻件的孔洞闭合规律研究提供了新的途径。法国的 SABY等[4]用数值模拟方法研究了球形孔洞在锻造过程中的闭合规律，并用XRD对锻件变形过程中的孔洞进行扫描，孔洞的真实形态和模拟形态高度吻合，从而验证了该方法的可行性。蒋智等[5]利用Deform软件对不同位置的孔洞进行分析，并用物理模拟的方法验证了数值模拟结果的合理性。崔振山等众多研究人员借助数值模拟方法研究了不同材料的孔洞闭合规律[6-10]。作为核电压力容器用钢508-Ⅲ，国内研究起步较晚，本文基于数值模拟软件Deform针对核电压力容器锻件生产过程中存在的大型钢锭内部孔洞压实困难的成形问题开展研究，分析孔洞演化的规律。

2 孔洞闭合与应力之间的关系

本次模拟采用Deform软件进行模拟，将508-Ⅲ钢的性能参数导入[11]，建立材料模型坯料为圆柱体，尺寸为φ200mm×300mm，为简化运算，根据圆柱的对称性，采取圆柱的1/2进行模拟计算，在坯料中心位置设置一个φ10mm的球体孔洞，如图1所示。对坯料进行网格划分，为更加精细孔洞的闭合情况，对孔洞周围进行网格细化；坯料温度设置为1200℃；上下模均为刚体，上下模与坯料之间的摩擦系数为0.7，上模压下速率为5mm/s。

图1 模拟所用模型

2.1 孔洞闭合过程中的形态变化

坯料在压缩过程中，孔洞的形态也在发生着变化，图2所示为孔洞在XOZ平面中不同变形量下的形态演变。从图2可看出，孔洞在坯料压缩过程中由球状渐变为椭球状，当椭球短轴减小到一定尺寸后，孔洞的内表面开始贴合在一起，最后逐渐闭合。在初始条件下孔洞的形状为直径10mm的圆球，当变形量增加到10%时，孔洞由圆球变为椭球，Z向为短轴方向，此时短轴长度为8.5mm，X向为长轴方向，长轴长度为10.46mm；当变形量为20%时，短轴缩短为3.4m m，而长轴增加到了12.28mm；当变形量达到28.6%时，短轴缩短为0，孔洞闭合。

图2 不同变形条件下的孔洞变化

2.2 孔洞边界的应力状态

根据圆柱镦粗的对称性，所选取孔洞周围的典型位置来分析孔洞边界的应力状态，取点位置如图3所示，分别标记为A、B、C、D共4点。4点的位置关系为：A点和D点分别是孔洞内表面与Z轴和X轴的交点，B点和C点是弧AD的三等分点。

图3 取点示意

一点的应力状态可以用对称的二阶张量σij表示，可以分为应力偏张量和应力球张量。应力球张量对塑性变形没有明显的影响，一般将其剥离出来，应力偏张量与塑性变形密切相关，在此引入Lode参数μ，若Lode参数μ相同，则表示两个应力状态相同，该表达式[12，13]为

式中μ——Lode参数；

σ1、σ2、σ3——主应力（MPa）。

当斜微分平面上只有正应力σ而没有切应力τ，此时的微分平面为主平面，平面上的应力为主应力，其中σ1＞σ2＞σ3，主平面的法线方向为主方向。

应力偏张量是二阶对称张量，因此也存在3个不变量，其中第三不变量J3′反映了应变的类型，当J3′＞0时表示伸长类应变，当J3′＝0时表示平面应变类应变，当J3′ ＜ 0时表示压缩类应变[14]。

在10%的变形量下，各点的应力状态如图4所示。A点受三向拉应力，3个主应力大小分别为40.1MPa、37.7Mpa、5.7MPa，此时J3′＜0，该点是压缩类应变；B点3个主应力为30.1MPa、20.8MPa、－5.9M P a，受两向拉应力、一向压应力，J3′＜0，该点也是压缩类应变；C点受一向拉应力、两向压应力，3个主应力为2.9MPa、－1.3MPa、－35.0MPa，此时J3′＜ 0，是压缩类应变；D点受三向压应力，3个主应力分别为－15.6M P a、－26.3MPa、－59.9MPa，J3′＜ 0，是压缩类应变。

图4 10%变形量下各点应力状态

在20%的变形量下，各点的应力状态如图5所示。随着变形量增大，A点还是受到三向拉应力，σ1增大到39.4MPa，σ2增大到35.8MPa，σ3降低到2.7MPa；B点应力状态不发生变化，σ1增大到33.7MPa，σ2增大到26.9MPa，σ3增大到－7.4MPa；C点的主应力方向没有发生变化，还是受到两向压应力、一向拉应力，σ1增大到6.2MPa，σ2增长到－4.7MPa，σ3增大到－35.5MPa；D点受三向压应力，随着变形量增大，σ1增大到－30.6MPa，σ2增大到－35.6MPa，σ3增大到－72.7MPa。孔洞周围皆是压缩类应变。

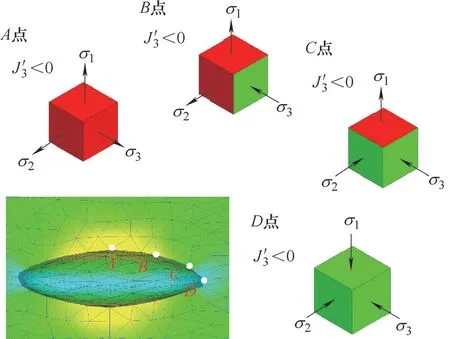
图5 20%变形量下各点应力状态

统计不同变形量下各点的应力状态，如图6所示。从图6可看出，在孔洞的闭合过程中，随着变形量的增大，3个主应力的方向不发生变化，且主应力的绝对值随着变形量的增大而增大。Lode参数μ随变形量的增大而增大。

图6 不同变形量下各点的应力状态

3 不同参数下孔洞闭合规律

由上述可知，孔洞沿Z轴方向（压缩方向）被压扁直至闭合，并沿X轴方向（垂直于压缩方向）拉长，为了描述孔洞的闭合情况，本文引入孔洞闭合率K，其表达式[15]为

式中D——孔洞的原始直径（mm）；

hZ——孔洞在Z轴上的投影长度（mm）。

0≤K≤1，当K＝0时，孔洞没有发生变化，K＝1时，孔洞完全闭合。

3.1 高径比对孔洞闭合的影响

本次模拟选取4组高径比不同的圆柱坯料，高径比分别为1、1.2 5、1.5、2，坯料尺寸分别为φ200m m×200m m、φ200m m×250m m、φ200mm×300mm、φ200mm×400mm。孔洞尺寸为φ5mm，坯料温度设置为1200℃；上下模与坯料之间的摩擦系数为0.7，上模压下速率为5mm/s。

不同变形量下的孔洞形态如图7所示。

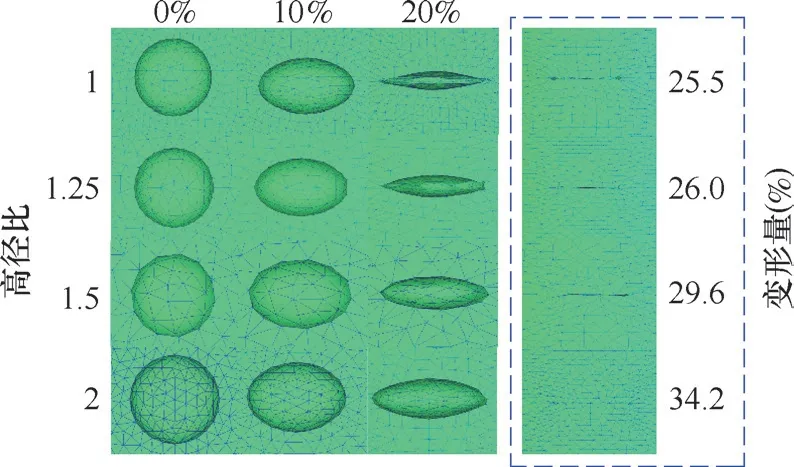
图7 不同变形量下的孔洞形态

由图7可知，孔洞的闭合度受高径比影响较大。在10%的变形量下，高径比为1的坯料，孔洞Z轴（压缩方向）高度缩短了1.76m m，K系数为35.3%；高径比为1.25的坯料，孔洞Z轴高度缩短了1.60mm，K系数为32.0%；高径比为1.5的坯料，孔洞Z轴高度缩短了1.31mm，K系数为26.2%；高径比为2的坯料，孔洞Z轴高度缩短了1.08mm，K系数为21.8%。当变形量增大到20%时，高径比为1的坯料，孔洞Z轴高度缩短了3.81mm，K系数为76.2%；高径比为1.25的坯料，孔洞Z轴高度缩短了3.64mm，K系数为72.9%；高径比为1.5的坯料，孔洞Z轴高度缩短了3.07mm，K系数为61.5%；高径比为2的坯料，孔洞Z轴高度缩短了2.56mm，K系数为51.3%。随着变形量的继续增大，高径比为1的坯料在25.5%的变形量下孔洞闭合，高径比为1.25的坯料在26.0%的变形量下孔洞闭合，高径比为1.5的坯料在29.6%的变形量下孔洞闭合，高径比为2的坯料在34.2%的变形量下孔洞闭合。由此可看出，在相同的变形量下高径比越大，K系数越小；随着高径比的增大，孔洞闭合的临界变形量越大。

统计上述坯料在不同高径比下的孔洞闭合率，如图8a所示。由图8a可知，孔洞闭合率与变形量程正相关，当孔洞尺寸相同时，在相同的变形量下高径比越小，孔洞闭合率越大。为了研究孔洞闭合快慢，将孔洞闭合率对变形量取微分得到K′，结果如图8b所示。由图8b可知，在相同的变形量下，高径比越小，孔洞闭合越快；以5%的变形量为分界点，在0～5%的变形量下孔洞闭合逐渐变慢，5%临界变形量之后，孔洞闭合逐渐加快并最终趋于稳定。

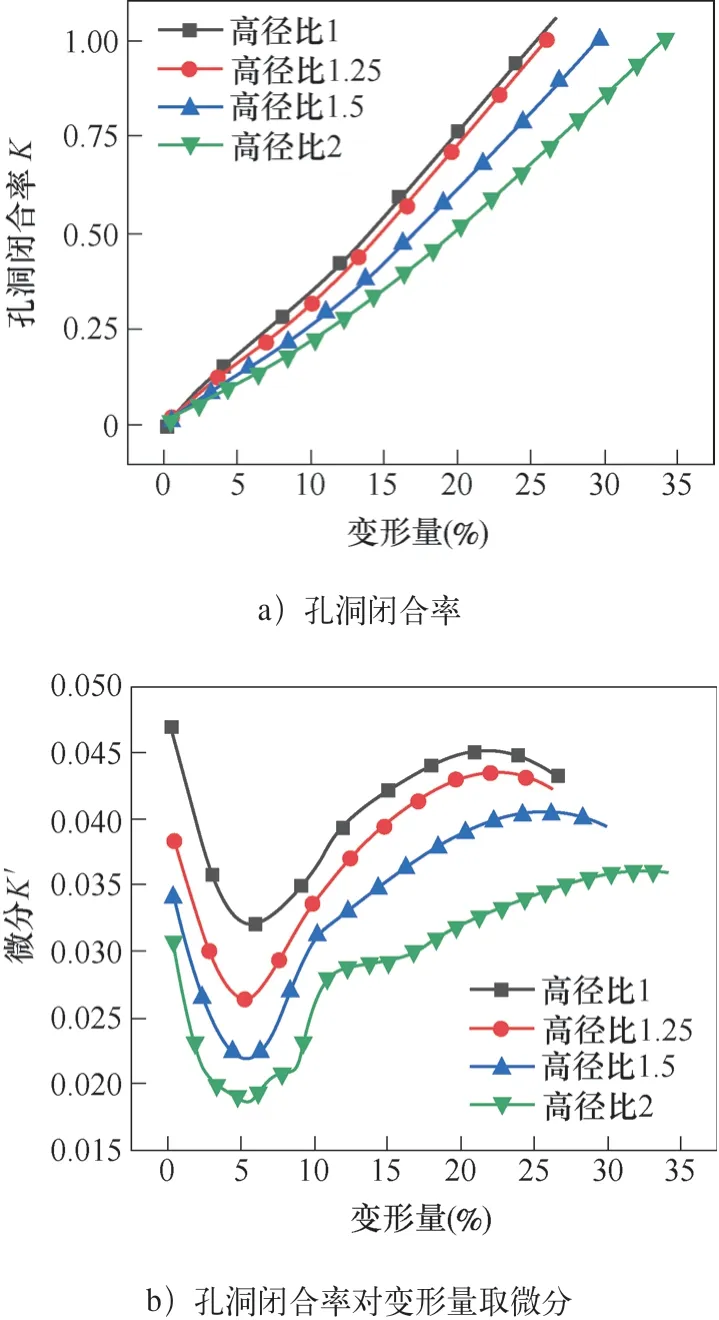
图8 不同高径比下的K和K′

3.2 孔洞尺寸对孔洞闭合的影响

本次模拟选取4组不同孔洞大小的圆柱坯料，孔洞尺寸分别为φ5mm、φ10mm、φ15mm、φ20mm，圆柱尺寸为φ200m m×400m m，坯料温度设置为1200℃；上下模与坯料之间的摩擦系数为0.7，上模压下速率为5mm/s。

图9所示为不同尺寸孔洞的坯料在不同变形量下的形态变化。从图9可看出，在10%的变形量下，φ5mm的孔洞在Z轴（压缩方向）高度缩短了1.08mm，孔洞闭合率K为21.8%；φ10mm的孔洞Z轴高度缩短了2.28mm，孔洞闭合率K为22.8%；φ15mm的孔洞Z轴高度缩短了3.49mm，孔洞闭合率K为23.2%；φ20mm的孔洞Z轴高度缩短了5.08mm，孔洞闭合率K为25.4%。

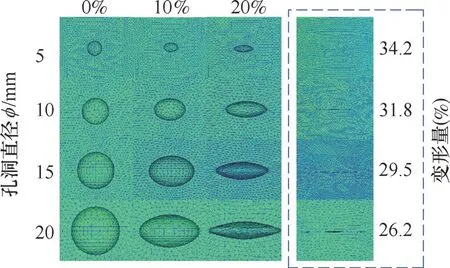
图9 不同变形量下的孔洞形态

当变形量增大到20%时，φ5mm的孔洞Z轴高度缩短了2.56mm，孔洞闭合率K为51.3%；φ10mm的孔洞Z轴高度缩短了5.34m m，孔洞闭合率K为53.4%；φ15mm的孔洞Z轴高度缩短了8.17mm，孔洞闭合率K为54.5%；φ20mm的孔洞Z轴高度缩短了11.05mm，孔洞闭合率K为55.2%。随着变形量的继续增大，φ5mm的孔洞在34.2%的变形量下闭合，φ10mm的孔洞在31.8%的变形量下闭合，φ15mm的孔洞在29.5%的变形量下闭合，φ20mm的孔洞在26.2%的变形量下闭合。由此可知，在相同的变形量下孔洞尺寸越大，孔洞闭合率K越大；孔洞尺寸越大，临界变形量越小。

不同变形量下的K和K′如图10 所示。

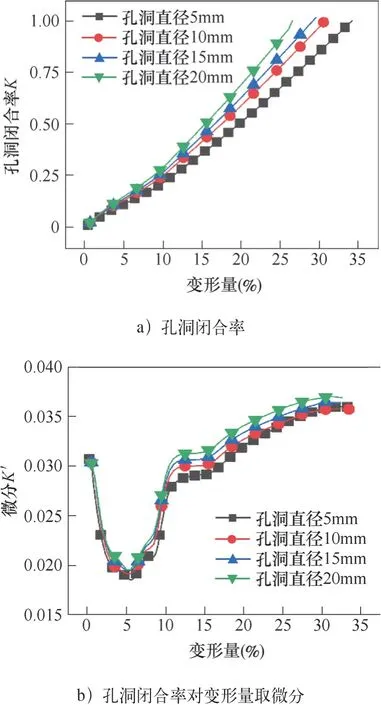
图10 不同变形量下的K和K′

由图10可见，当坯料高径比相同时，在相同的变形量下孔洞越大，孔洞闭合率越大。孔洞闭合的快慢受孔洞尺寸的影响较小，不同尺寸孔洞的K′曲线几乎重合；同样以5%的变形量为分界点，在0～5%的变形量下孔洞闭合逐渐变慢，5%临界变形量下，孔洞闭合逐渐加快。

4 结论

1）坯料在压缩的过程中，孔洞的形态由球形逐渐变成椭球形，最终闭合；孔洞周围各点的3个主应力在变形过程中逐渐增大，且Load参数μ随变形量的增大逐渐增大；通过计算应力偏张量的第三不变量J3′ 得到在变形过程中孔洞周围的变形状态均是压缩类应变。

2）当孔洞尺寸一定时，在相同的变形量下高径比越大，K系数越小，随着高径比的增大孔洞闭合的临界变形量越大；当坯料高径比一定时，在相同的变形量下孔洞尺寸越大，孔洞闭合率K越大，孔洞尺寸越大，临界变形量越小。

3）孔洞闭合的快慢受坯料的高径比影响较大，在相同的变形量下高径比越小，孔洞闭合越快；以变形量的5%为分界，在0～5%的变形量下孔洞闭合逐渐变慢，5%临界变形量下，孔洞闭合逐渐加快。

5 生产应用

在生产中用到的是83t铸锭，首先压钳口、倒棱、气割锭尾；此时坯料尺寸为φ1750mm×3350mm，在150MN的水压机上使用上下宽砧对坯料进行整体镦粗，以5mm/s的速度进行下压，变形量为50%。锻造结束后采用GB/T 6402—1991《钢锻件超声波检验方法》2级标准进行无损检测，结果表明，采用上述压实工艺后，坯料合格率100%，不存在变形死区，铸锭内部的缩孔、疏松缺陷得到有效愈合。