助力高中听障学生数学概念学习的可视化教学策略
2024-06-12严丽萍

【摘要】 高中数学概念教学具有情境复杂、表征多元、规律内隐、高度抽象等特点。聋校高中数学教师在教学中可充分利用听障学生视觉学习优势,采用情境创设可视化、抽象过程可视化、思想方法可视化、解决问题可视化等策略,帮助听障学生深度理解数学概念,发展数学学科核心素养。
【关键词】 数学概念;可视化教学策略;高中听障学生
【中图分类号】 G762
【作者简介】 严丽萍,中小学高级教师,浙江省杭州文汇学校(杭州,310018)。
《普通高中数学课程标准(2017年版2020年修订)》要求重视信息技术运用,优化课堂教学,转变教学方式,为学生理解概念创设背景,为学生探索规律启发思路,为学生解决问题提供直观[1]。可视化教学是指利用图形图象、动画视频等视觉表征手段,以及思维导图、知识地图等视觉认知辅助工具,将抽象的教学内容具体化,经由相应的教学活动内化为学习者的认知结构[2]。可视化教学可以利用丰富的可视化资源,通过情境化、引导性和形象直观的视觉表征方式,促进听障学生的抽象思维能力发展[3];也可以将复杂的教学内容具体化、视觉化和形象化,有效调动听障学生的形象思维,激发他们的情感[4]。聋校高中数学概念教学具有情境复杂、表征多元、规律内隐、高度抽象等特点,教师可充分利用听障学生视觉学习优势,开展可视化教学,帮助听障学生建立数学“高度概括抽象形式”与“直观可见可操作形式”之间的关联,为听障学生理解数学概念创情境、拓路径、优策略。
一、情境创设可视化,揭示数学概念本质属性
情境创设可视化是指将抽象的数学问题具体化、形象化,利用文字、图片、视频等多种媒介,构建生动、立体和直观的最少受限学习情境,帮助听障学生多角度、多层次理解和掌握数学概念。教师可以创设联系生活实际的数学教学情境,采用生活趣味题、微课和视频(配以字幕、增加注释)等形式,将数学概念核心知识用有趣的情境予以呈现及凸显,帮助听障学生更好地理解数学概念。
例如,在三角函数“任意角”概念教学中,为了探讨生活中是否有超出0°~360°的角,教师可以用蹦床比赛中翻转动作“前屈两周”“后屈三周半”的视频,以及贴近学生生活实际的摩天轮旋转一周又一周的视频等,从实际问题直观的共同特征中提炼出角的“旋转方向”“旋转量”这两个关键要素,进而揭示任意角概念的本质属性和引入任意角的必要性。教师还可以利用可视化的数学教学软件(如GeoGebra软件)动态展示角的旋转:利用渐开线刻画角,拖动滑动条(对应变量a)可以发现,随着a的变化,角的终边落到不同象限,当a>0时角呈逆时针旋转,a<0时角呈顺时针旋转。学生通过观察,从旋转方向和旋转量两个方面进一步理解任意角的概念。
联系生活实际,借助信息技术等手段创设动态直观的可视化情境,将数学问题变得形象具体、生动有趣,可以帮助听障学生突破既有的思维定势,建构新的数学概念,从而有效提高数学概念学习成效。可视化情境的直观视觉信息不仅可以提高听障学生的学习兴趣和积极性,直接驱动学习行为,还有助于听障学生强化工作记忆提取和信息加工。可视化情境揭示了知识起源、形成及发展过程,把数学抽象概念转化为易于理解的形式,有利于听障学生探索一般规律,从现实生活中抽象出数学模型,揭示数学概念本质属性,实现对数学概念的“新发现”和“再创造”。
二、抽象过程可视化,转化数学概念多元表征
抽象过程可视化是指把数学概念的抽象过程,通过可视化手段(包括图形、图表、动画等)进行表达和解释,以帮助学生更好地理解和掌握这些概念。数学概念是高度抽象的,抽象过程是内隐的,抽象层次是多元的,这就导致听障学生学习数学概念时困难重重。数学概念一般有多元表征、多种理解,学习概念的关键是建立各种表征之间的联系,学会选择、使用和转化,这样才能有效运用概念解决问题。以“函数”概念为例,我们通常在头脑中联想到某个具体函数的图象或某个具体函数的解析式,也可能想到“函数是两个数集之间对应关系”等语言表述,这些都是“函数”概念表征。
多元表征是符号表征、语言表征、操作表征、情境表征、图表表征等外在表征形式的综合。多元表征转换是理解数学概念的有效手段,单一表征往往难以充分揭示数学概念本质。文字的叙述性表征可以传递抽象经验和信息,图表的描绘性表征便于传递具体经验和信息。图表表征将抽象问题直观化,既有形象性,又有抽象性。高中听障学生数学概念学习困难的一个重要原因就是对数学概念难以进行适宜的表征,不能在多种表征之间进行自由转换。对听障学生而言,图表表征往往优于文字、符号表征。图表表征巧妙转化数形两类表征,更有利于听障学生直观、形象地理解和解决问题。
例如,在“函数”概念教学中,教师可以联系实际生活中水、电、煤气的收费,以及平均气温变化图、心电图等,用表格、解析式、图象形式等多元表征函数概念,促进学生对函数概念的理解。
案例1:程同学的表哥是一名大学生,他利用暑假时间去肯德基打工,报酬按16元/小时计算。请填写下表并回答问题。
[工作时间t(小时) …… 1 5 10 15 20 t …… 报酬m(元) …… …… ]
(1)在本案例中,哪些是常量?哪些是变量?
(2)能用t的代数式来表示m的值吗?如果时间t取某个特定值,报酬m相应可以取几个值?
(3)两个变量之间有什么关系?哪个变量一经确定,另一个变量也随之确定?
案例2:画出杭州2023年11月29日的气温变化图,并根据图象回答问题。
(1)在本案例中,哪些是变量?
(2)如果时间h取某个特定的时间,温度T相应取几个值?
(3)两个变量之间有什么关系?哪个变量一经确定,另一个变量也随之确定?
上述两个案例均为贴近听障学生生活经验的实际问题。教师利用问题引导学生动手画图,借助可视化手段辅助他们进行“函数”概念的多元表征转换。学生借助表格、图象和解析式三种不同表征形式理解函數概念,更容易抽象出函数概念的本质属性。可视化的函数概念抽象过程,正是听障学生经历辨别(刺激模式)、分化(各种属性)、类化(共同属性)、抽象(本质属性)、检验(确认)、概括(形成概念)、形式化(符号表达)等概念形成的整个数学抽象过程[5]。利用可视化教学策略建立多元表征联系,不仅可以让听障学生深刻把握数学概念的本质和非本质属性,建构良好的知识结构,而且可以增强听障学生全面审视问题的能力,形成优良的思维品质。同时,涉及视觉、运动觉、触觉等多感官通道的数学内在类比表征,也有助于听障学生对数学概念的意义进行理解和建构。
三、思想方法可视化,理清数学概念内隐规律
高中数学新课标把“双基”扩展为“四基”,指出高中生需要掌握基础知识、基本技能、基本思想和基本活动经验。因此,高中听障学生除了获得必要的数学知识技能外,还要能感悟数学的基本思想,积累数学思维活动和实践活动的经验。数学思想方法是数学知识内容的精髓,是对数学的本质认识,是数学学习的一种指导思想和普遍适用的方法[6]。通常所说的数形结合、分类讨论、函数与方程、化归等,都可以称为数学思想方法。在高中数学概念教学中,教师往往重视知识技能传授,忽视渗透在概念中的思想方法。这是由于思想的感悟和方法的形成是抽象的、隐性的、过程性的,可意会,难以言传。若将其可视化,呈现数据内在关系,进行直观的观察、视觉的感知,有助于学生揭示数学本质、锤炼思维品质和发展核心素养。
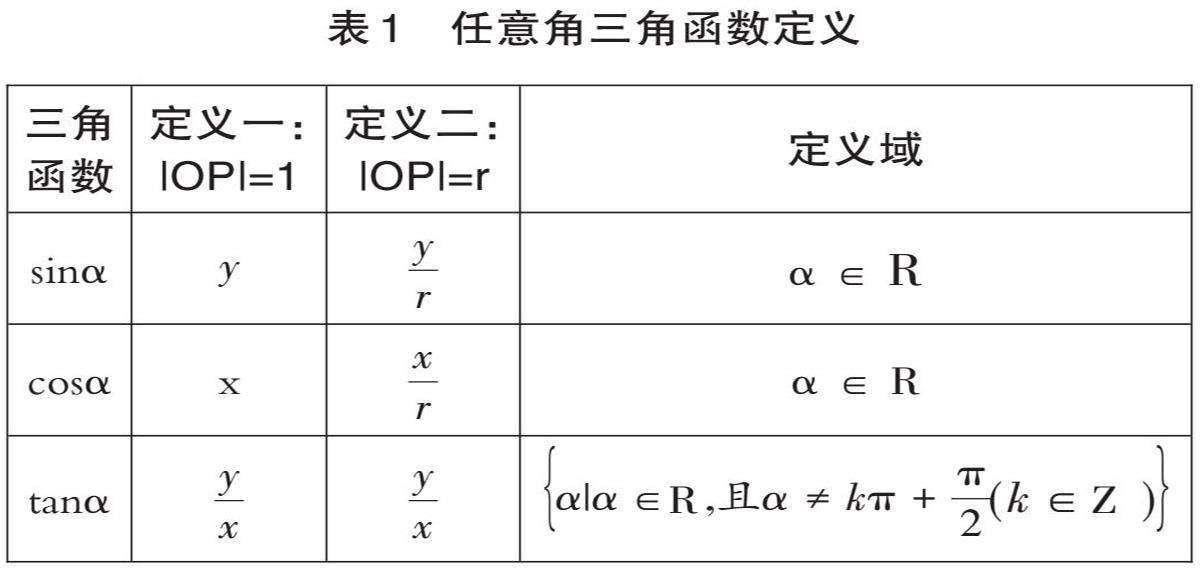
例如,教师在“任意角的三角函数”概念教学中,可以渗透数形结合、化归和分类讨论思想方法。首先,采用数形结合的方式复习初中锐角三角函数定义,激活高中听障学生已有的三角函数概念经验。然后,从锐角扩展到直角坐标系中第一象限任意角,借助信息技术揭示终边上点的位置改变时,正弦、余弦、正切的比值不变的数据关系,把第一象限任意角三角函数化归为锐角三角函数,找到新旧知识连接点。接着,用分类讨论思想方法,探究角的终边在第二象限、第三象限、第四象限时三角函数值的变化,总结得出任意角三角函数值的终边定义。同时渗透第二象限、第三象限、第四象限任意角的三角函数都可以化归为第一象限任意角的三角函数,为后续学习诱导公式奠定基础。还可以探究终边上点到原点距离为1的特例,得出任意角三角函数的单位圆定义。最后,及时归纳总结,给出任意角三角函数定义表格(见表1),让学生自己补充完整,促进其对所学数学概念的理解和掌握。
表1 任意角三角函数定义
[三角函数 定义一:|OP|=1 定义二:|OP|=r 定义域 sinα [y] [yr] α ∈ R cosα x [xr] α ∈ R tanα [yx] [yx] [α|α ∈ ,且α ≠ kπ+π2][(k ∈ )] ]
数学思想方法是隐性知识,它源于数学知识又超越数学知识,是对数学知识的本质认识,也是对数学内在规律的理性认识。在数学概念教学中,采用几何画板等可视化工具直观揭示数据关系、图形显示数形关系及图表归纳类比等可视化教学策略,不仅可以帮助听障学生在头脑中建构概念图式,而且能够引导他们理清数学概念背后的隐性规律,帮助他们从概念形成过程中抽象概括出数学思想方法,并用掌握的思想方法解决数学问题,从而达到提升数学学科核心素养的目的。
四、问题解决可视化,促进数学概念迁移运用
问题解决可视化旨在通过图形、图表、动画、模拟、实物模型等直观手段,将抽象的数学概念、关系、过程和问题解决方案呈现出来,以增强学生对数学概念的理解、记忆和应用能力。问题解决可视化,不仅可以深化高中听障学生对数学概念的理解,而且能提高他们在不同情境中识别和应用数学模式的能力,促进数学概念的迁移运用。
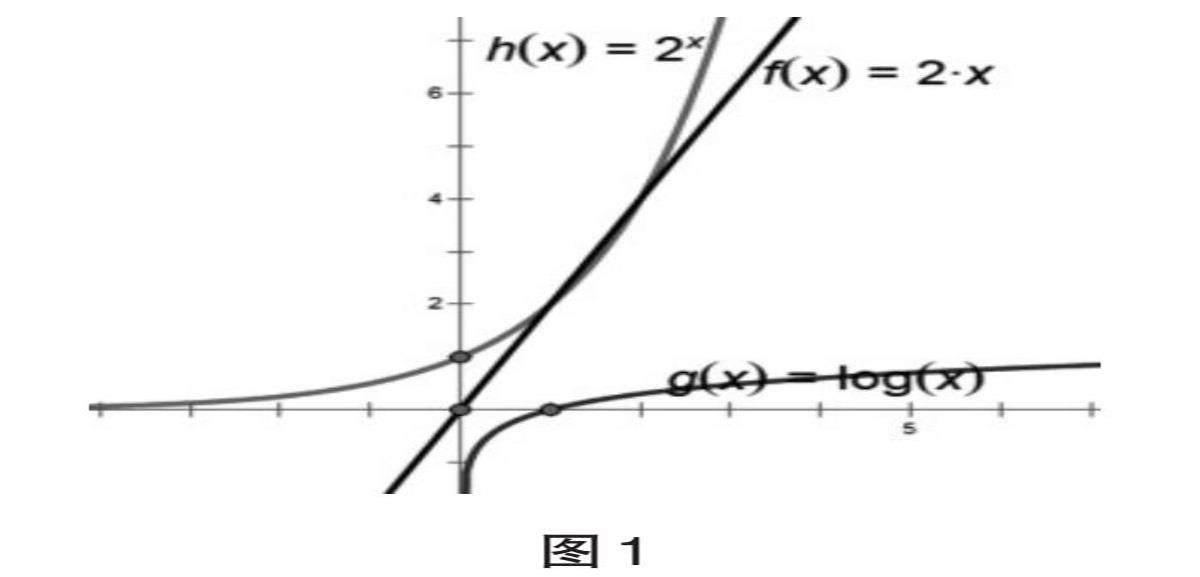
例如,针对“画出一次函数y=2x、对数函数y=lgx和指数函数y=2x的图象,并比较它们的增长差异”这一问题,教师用几何画板在同一个直角坐标系中画出3个函数图象(见下页图1),让听障学生直观感受3个函数的增长差异,理解“直线上升”“对数增长”“指数爆炸”的含义,进而在后续学习中能根据对不同函数增长差异的认识,选择适合的函数类型建构数学模型,刻画现实问题的变化规律。利用可视化工具展示不同数学概念之间的相似性和差异性,揭示内在结构和联系,可以帮助学生理解不同类型的函数的增长特性并进行合理类比,从而在新情境中选择合适的模型。教师也可以鼓励听障学生使用思维导图、概念图等可视化工具记录自己的解题思路,反思问题解决过程中的数学概念运用,培养他们认识和监控数学认知活动的元认知能力。
问题解决可视化,能强化听障学生的视觉学习,让他们快速直观地理解数学问题的本质,突破纯文字和符号表述带来的认知局限。人脑对视觉信息的处理速度和记忆效率通常高于文字信息。用思维导图展示数学解题步骤和思维过程,能够帮助学生更好地记住解决问题的方法和策略。教师可以通过模拟、仿真或实际操作等进行可视化教学,如使用几何画板、动态数学软件等工具,让听障学生动手操作,直接看到数学模型的变化,从而有效提高他们的实践应用能力。可视化教学策略在问题解决中的应用,能够帮助听障学生夯实数学应用基础,培养他们识别和应用数学模型的能力,增强在不同情境中灵活迁移运用数学知识的意识与技能,从而拓展数学学习的深度和广度,促进核心素养的发展。
综上所述,在数学概念教学中,教师可采用情境创设可视化、抽象过程可视化、思想方法可视化和问题解决可视化等策略,构建“所见即所得”的学习情境,实施“可见可操作”的学习方式,把抽象的数学概念图形化表达、模式化建构,揭示数学概念本质,为高中听障学生的数学概念学习减负提质。
【参考文献】
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[S].北京:人民教育出版社,2020.
[2]张志勇.基于GEOGEBRA的数学实验与可视化教学[M].长春:东北师范大學出版社,2018.
[3]郑曼.聋生可视化教学资源研究[D].开封:河南大学,2013.
[4]王茂娟.基于翻转课堂的聋生初中数学可视化学习资源设计与应用研究[D].成都:四川师范大学,2019.
[5]蒋海燕.中学数学核心素养培养方略[M].济南:山东人民出版社,2017.
[6]钱佩玲,邵光华.数学思想方法与中学数学[M].北京:北京师范大学出版社,2014.
(责任编辑:黄春露)