巧用空间向量处理一类翻折问题

晏婧 章建荣

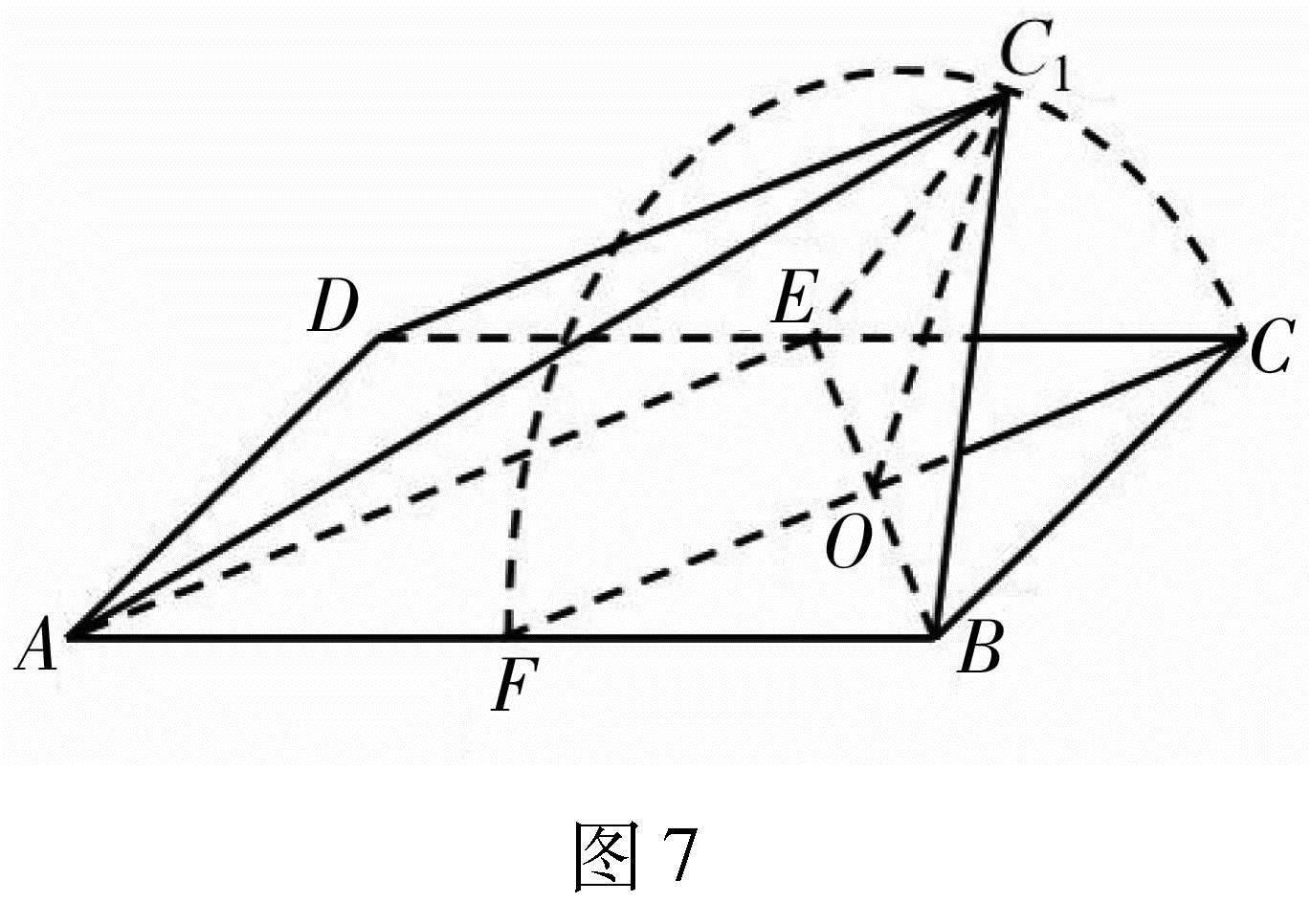
立体几何中翻折问题是常见的问题，此类问题研究线线、线面的平行和垂直，还涉及与动点关联的有关空间角度和距离的问题，旨在考查学生的空间想象能力、逻辑推理能力及计算能力，此类问题比较灵活，要在变化中寻找规律，对学生的思维的灵活性和知识的迁移能力有一定的要求.

类型一 翻折中存在性的定性判断

A．存在某个位置，使得直线BD与直线AC垂直

B．存在某个位置，使得直线AB与直线CD垂直

C．存在某个位置，使得直线BC与直线AD垂直

D．对任意位置，三对直线“AC与BD”，“CD与AB”，“AD与BC”均不垂直

解析：矩形在翻折前和翻折后的图形如图1（1）、图1（2）所示．在图1（1）中，过点A作AE⊥BD，垂足为E，过点C作CF⊥BD，垂足为F，由边AB，BC不相等可知点E，F不重合．在图1（2）中，连接CE，对于选项A，若AC⊥BD，又知BD⊥AE，AE∩AC=A，所以BD⊥平面ACE，所以BD⊥CE，与点E，F不重合相矛盾，故选项A错误；

对于选项B，若AB⊥CD，又知AB⊥AD，AD∩CD=D，所以AB⊥平面ADC，所以AB⊥AC，由AB

对于选项C，若AD⊥BC，又知DC⊥BC，AD∩DC=D，

所以BC⊥平面ADC，所以BC⊥AC，

已知AB=2，BC=22，则BC>AB，所以不存在这样的直角三角形，故选项C错误.

由以上可知选项D错误．故选B．

评析：这种翻折中有关异面直线垂直的存在性问题，旨在考查平面问题空间化，将异面直线垂直的问题，核心是转化为线面垂直，将存在性的问题通过假设推理，加以论证，有效的考查空间想象能力和逻辑推理.

但随着题目难度增加，学生往往束手无策.平面图形绕一条定轴翻折问题，几何体的动态呈现，使思维更具发散性，一个比较有效的思考方向是抓住点的运动轨迹，寻找规律.

如图2所示，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折的过程中， △ABD是翻折面，BD是翻折轴，AE⊥BD，在翻折的过程中，点A的翻折运动的轨迹就是以E为圆心，AE为半径的半个圆周，而且这个圆周面和BD是垂直的，这个规律便是处理翻折的问题重要突破口.

评析：借助翻折的规律，通过建立空间坐标系，用圆的参数方程表示动点，用代数的思想来研究动态的翻折问题，有效地降低了逻辑推理的难度，体现了数形结合的思想.

类型二 翻折中存在性的定量计算

－BCD，若在翻折过程中，存在某个位置，使得A′D⊥BC，则x的取值范围是．

评析：理清翻折前后的变量与不变量，一般情况下，位于旋转轴同侧的平面图形的几何量及位置关系是保持不变的，特别是垂直关系，利用空间向量来处理，有效地降低了空间想象的难度，同时还能判断存在性点的位置情况，即夹角为锐角时才会出现垂直的可能，体现了代数法的优势.

类型三 翻折中存在性综合应用

例3 在矩形ABCD中，AB=2AD=2，E为CD的中点，将△CBE沿直线BE翻折至△C1BE的位置，則（）.

B．翻折过程中，存在某个位置的C1，使得BE⊥AC1

C．翻折过程中，四棱锥C1－ABED必存在外接球

D．当四棱锥C1－ABED的体积最大时，以AC1为直径的球面被平面C1BE截得交线长为π

翻折是联结平面与空间、变量与不变量的重要纽带，立体几何翻折问题打破了一般立体几何问题的定势思维，考查学生的空间想象等能力，所以求解此类问题应从翻折的规律出发，借助空间向量处理空间的平行、垂直和有关角度的问题，这不失为一种行之有效的方法.