基于数学实验培养直观想象素养的教学路径

基金项目  2023年湖北省教育规划课题“素养立意下高中数学‘教考衔接的路径研究”（2023JB506）.

【摘  要】  《中小学实验教学基本目录》的颁布，赋予了数学实验教学新的背景.在几何与代数主题教学中，以《中小学实验教学基本目录》的基本数学实验活动为载体，通過“创设情境、基于问题设计方案”“选择模式、开展实验探讨数形联系”“观察发现、分享交流聚焦几何直观”“归纳总结、验证展示提升素养”等教学路径，能更好地落实培养学生直观想象素养的要求.

【关键词】  数学实验教学；几何与代数；直观想象素养

1  数学实验教学的新背景

著名数学家欧拉曾说，数学这门学科，需要观察，还需要实验.在国内，数学实验教学的研究已有不少成果.数学实验的理论研究（概念、分类、模型）和数学实验教学应用的相关研究已逐步完善，数学实验教学的价值和意义也被认为可以激发学生的学习兴趣、提高学生的动手操作能力、培养学生的创新与探究精神，从而提升学生核心素养.2023年11月底，教育部教育技术与资源发展中心（中央电化教育馆）组织专家研制并发布了《中小学实验教学基本目录》（以下简称《基本目录》）.《基本目录》中数学实验是指以探索数学现象、发现数学规律、验证数学结论、解决数学问题为目的，运用有关工具（如纸笔、数学模型、测量工具、作图工具、计算机、图形计算器等），在数学思维活动的参与下，以学生数学化操作为特征的数学探究活动［1］.因此，数学实验教学属于探究活动范畴，具有使得数学对象直观化的直接功能.《基本目录》中普通高中数学实验教学基本目录包括数学实验活动48个，其中几何与代数主题中的基本实验活动为14个（必修部分为8个，选择性必修部分6个）.《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课标》）指出，几何与代数是高中数学课程的主线之一，在必修课程与选择性必修课程中，要求突出几何直观与代数运算之间的融合，即通过形与数的结合，感悟数学知识之间的关联.所以，我们完全可依托数学实验直观数学对象的功能，在几何与代数主题课堂教学中融入数学实验，突出几何直观与代数运算之间的融合，培养学生的直观想象素养.

2  基于数学实验教学的直观想象素养培养路径

《课标》指出，直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.具体要求是学生能够想象并构建相应的几何图形，发现图形与图形、图形与数量的关系，探索图形的运动规律；能够掌握研究图形与图形、图形与数量之间关系的基本方法，借助图形性质探索数学规律，解决实际问题或数学问题；能够用图形探索解决问题的思路，形成数形结合的思想.笔者曾提出将“直观想象素养水平一”理解为“数”与“形”之间的直译；“直观想象素养水平二”理解为“数”与“形”之间运用联想、知识迁移所反映出来的联系；“直观想象素养水平三”可以理解为“数”与“形”之间通过知识的创新性、数学分支之间及学科之间综合应用性所反映出来的“深层次”的联系［2］.因此我们可以将研究图形位置关系、研究形与数之间的联系等作为实验目的，在课堂教学中融入相应的数学实验，达到培样学生直观想象素养的目的.

那么这个教学路径是怎样的呢？实际上，课堂中数学实验教学的一般过程可总结为“提出问题—设计方案—开展实验—观察发现—分享交流—探究原因—得出结论”，直观想象素养培养路径可以从这些流程的步骤着力.

2.1  创设情境，基于问题设计方案

数学实验教学作为课堂教学环节的一部分，要服务整个课堂教学进度.那么数学实验的目的和设计就要融入整个课时教学内容，为数学实验创造合理的数学情境，让学生参与情境中的实际活动并从中发现和提出问题.

实验案例：探究祖暅原理在构造几何体推导球的体积公式中的应用

本案例是《基本目录》内普通高中数学实验教学基本目录部分立体几何初步主题中“探究球的表面积和体积”“祖暅原理的探究与应用”两个基本实验活动的综合体现，数学实验目的定位为研究形与数之间的联系.那么其情境与问题的设计如下.

情境引入：在2023年杭州亚运会上，中国女篮战胜劲敌日本队，成功卫冕亚运会冠军.已知女子篮球标准比赛用球为6号球，其直径为22.6厘米，请问这个篮球的体积是多少？

问题1：你有什么办法测出该篮球的体积吗？

设计意图：以学生生活中常见的篮球为研究对象，结合当前热门话题引出课题，将生活问题转化为数学问题，既体现了数学的生活化，提高了学生的学习兴趣，也增强了民族自豪感.

设计数学实验方案（圆柱容球实验）：如图1，实验器材包括一个面盆，等高的圆柱（内空）、球、圆锥，足够的水.将圆柱中装满水，应用排水法让学生测量圆柱分别容球、容椎体后在面盆中排出的水的体积，从而猜测球的体积和圆柱体积之间的关系.

设计意图：通过实验直观感知球的体积与圆柱、圆锥体积有关，并引导学生建立形与数之间关联，落实直观想象素养水平一的培养，即感知圆锥排出水的体积为圆柱水中体积的13，球排出水的体积为圆柱水中体积的23，从而引出介于圆锥与圆柱之间的球的体积为23Sh的猜测，为后续构造几何体，推导体积公式提供启示.

2.2  选择模式，开展实验探讨数形联系

有研究总结了数学实验教学的三种模式，即理解型、验证型、探究型数学实验［3］.每种模式的活动实施程序有所差异.案例1的数学实验适用探究模式，该模式实施程序如下：

在操作探究的环节，可通过多个问题引导，让学生进行实验探究.例如：

问题2：你能猜测出球的体积和球的半径R之间的关系吗？

设计意图：从具体到抽象，引发学生思考形与数之间的关系.

问题3：柱体体积公式是如何推导出来的？

学生活动：回答柱体体积公式的推导过程，复习回顾祖暅原理，即两个几何体在等高处所截得的截面处处相等，所以可以推测它们的体积相等.

2.3  观察发现，分享交流聚焦几何直观

数学实验教学中学生将通过實践活动，自主探究数学知识，提高自己的数学思维能力和问题解决能力，体现的是“在数学思维活动的参与下，以学生数学化操作为特征的数学探究活动”.

问题4：如何借助祖暅原理求半径为R的半球体积？

学生活动：根据祖暅原理，思考构造一个与半球体积相同的几何体.

问题5：构造这样的几何体需要满足什么条件？

学生活动：借助祖暅原理，考虑构造一个与半球同时夹在两个平行平面之间，且与半球在任意等高处的截面面积相等的几何体.

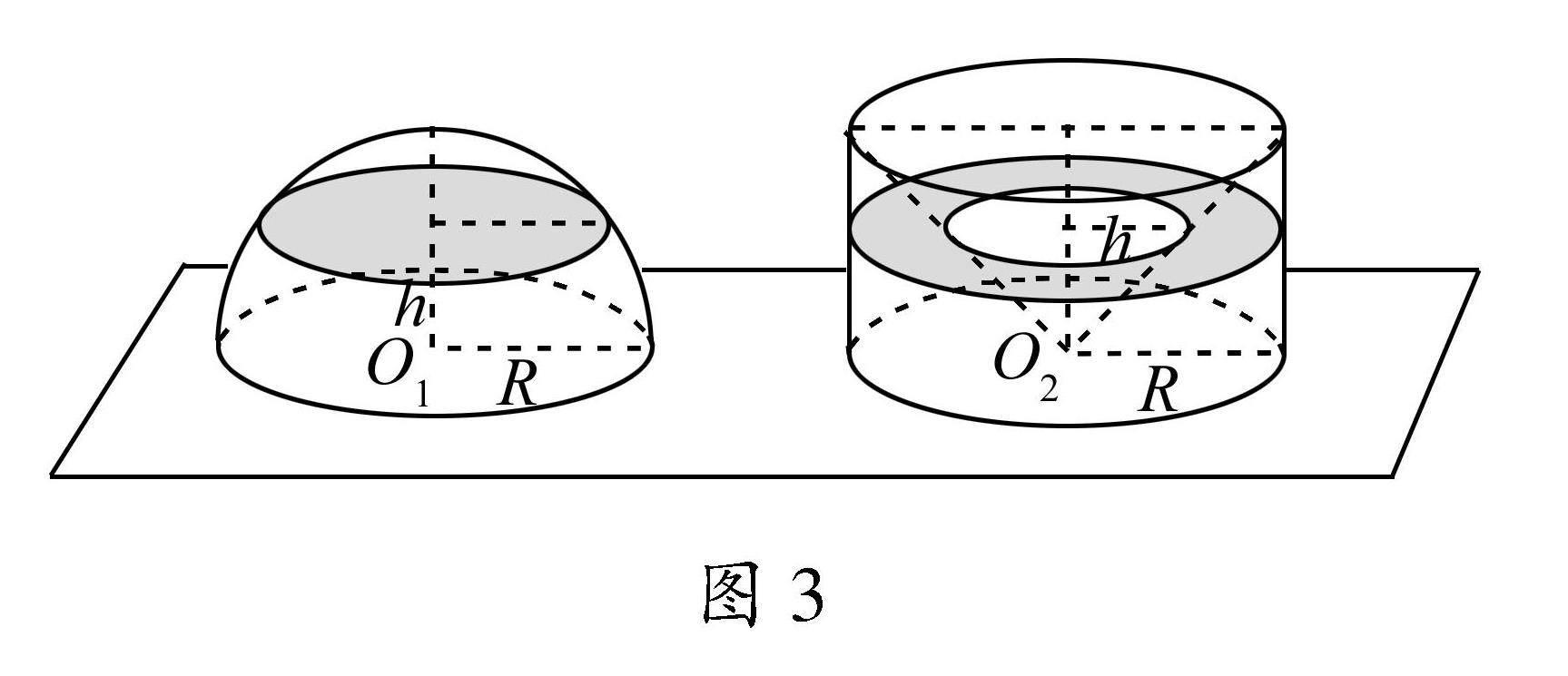
问题6：如图3，半径为R的半球在高度为h处（0≤h≤R）的截面面积是多少呢？

生1探究过程：截面面积为S=πR2-πh2.

教师引导：S可以看作是大圆面积减小圆面积，又S=π（R2-h2）等同于在与半球等高处的截面图形是一个圆环，这样累积起来，进而构造出一个底面半径和高均为R的圆柱，其中挖去一个倒置的底面半径和高均为R的圆锥后（此时与图1中所示的几何体联系），剩下的几何体.该组合体的体积就是与它等底等高的半球体积.同时利用GGB数学软件演示，印证截面面积始终相等.

设计意图：建立数与形之间的联系，是数学实验中“数学化操作”的主要特征.也是数学实验设计中关键的步骤，教师要做好引导.数学实验根据分类有基于传统工具的数学实验和基于计算机的现代数学实验，利用GGB数学软件演示也是从现代数学实验的角度来验证结论.

问题7：如何推导半径为R的球的体积公式？

学生活动：推导球的体积公式：V半球=V圆柱-V圆锥=πR3-13πR3=23πR3，V球=43πR3

2.4  归纳总结，验证展示提升素养

数学实验与物理、化学实验不同，学生在完成实验任务时，往往难的不是实验操作，而是在“数学化操作”中缺乏提炼和思考，缺乏“数与形”之间的深入探究，从而有时难以顺利达到实验目的.因此，需要总结交流数学实验过程中学生的各种数学思维，使得学生能够在交流、分享的活动中基于几何直观深入理解数学知识，提高学习效果和培养直观想象素养.

问题8：除了图3中几何体构造，利用祖暅原理，可设计哪些与它等积的几何体？

学生展示1：可将截面面积转化为S=（πR）2-（  πh）2，这样可以转化为以  πR的正方形面积减去以  πh为边长的小正方形面积（如图4，其中内含小正方形的边长可通过相似比求得为  πh）.这样累积起来，就可看做是一个正方体中挖去一个四棱锥（四棱锥顶点恰好为底面的中心，如图5所示）.

值得一提的是，四棱锥的顶点在底面正方形中任何位置都可以几何直观，如图6.

学生展示2：可将截面面积转化为S=π（R+h）·π（R-h），构造的等积几何体可以看做由一个三棱柱中挖去一个四棱锥得到，几何直观如图7所示.

设BE距底面的高度为h，由相似三角形的比可得BEHC=ABAC=1-BCAC=1-hR，又HC=πR，BE=πR-πh=π（R-h），从而BI=π（R+h）.又BF=BE=π（R-h），所以截面面积为S=BI×BF=π（R+h）·π（R-h），符合截面面积转化公式.

教师引导：分别通过GGB呈现学生展示1，2中的截面积变化是否相等，帮助学生深入理解“祖暅原理”.

设计意图：此环节的设计，是鼓励学生自主探究和创新，让学生在数学实验中发挥自己的想象力和创造力，并能通过数学软件验证实验结果，提高数学实验教学的趣味性和吸引力.从现代数学实验验证的角度来看，此实验既是对球的体积的实验总结，也是“祖暅原理的探究与应用”基本实验活动的深入推进.

3  结语

数学实验教学是适应现代教育教学改革要求的一种教育方式，特别是在几何与代数的课堂教学中直观想象素养的落地需要数学实验这个载体.从而在设计实验教学各个环节时，要以直观想象素养内涵中研究图形位置关系、研究形与数之间的联系等为实验目的，挖掘生活资源，拓宽数学实验教学的路径，激发学生兴趣，帮助学生理解数学知识、体验探究过程、培养学生的创造才能.

参考文献

［1］  康杰.开展数学实验 培养创造才能［EB/OL］.（2023-11-24）［2023-12-06］.http：//www.moe.gov.cn/jyb_xwfb/moe_2082/2023/2023_zl24/202311/t20231123_1091841.html.

［2］  周威.试谈一道高考题中直观想象素养各水平的体现［J］.教学考试，2020（11）：65-67.

［3］  周武冬. 数学实验教学及其在高中数学教学中的应用研究［D］.延安：延安大学，2023（06）.

作者简介

周威（1985—），男，中学一级教师，硕士，恩施州教育科学研究院高中数学教研员；研究方向为教育评估与高中数学教育；发表论文80余篇，出版专著1部.