小学数学教学中几何画板运用探究

赵 勤（贵州省纳雍县百兴镇第二小学）

近年来，随着教育信息化理念的普及和深化，信息技术被广泛地融入教学活动之中。数学是一门抽象的学科，具有很强的严谨性和逻辑性。小学数学学习是理科学习的基础，对学生的终身发展具有至关重要的影响。几何画板作为信息技术的产物之一，其以图像变化、数据呈现为主，将图像投影、数据分析、动态演示等技术有机融合，有力地促进了教学改革工作的深入。小学数学教师更应立足教学实际科学构思课程，将“几何画板”与“数学”巧妙融合，以独特的学习方式促进学生数学素养提升。

一、巧用几何画板，激活学生学习兴趣

在小学阶段，学生仍以具象思维为主，尚未实现思维的完全转换。尤其在小、中年段数学学习中，学生对抽象的数学概念理解较为困难，学习热情度大打折扣，影响学习效率。几何画板作为信息技术的重要体现之一，其将数学概念以图像的形式呈现在学生眼前，其以点、线、面为基本元素，软件中将变化、旋转、平移、缩放、反射等多种功能有机融合，不仅能强化学生对所学内容的理解，还能帮助学生将“三维立体”与“二维平面”科学转换，有效激活了学生对数学知识的学习兴趣。

基于此，小学数学教师应立足教育实际，结合所学内容为学生科学构思课程，以几何画板为辅助工具，用趣味数学知识激活学生的学习兴趣。

在苏教版《义务教育教科书·数学》二年级上册中“观察物体”一课中，本课学习为几何学习的“基础”，以观察为主，让学生通过实际观察、比较，初步体会从不同的位置观察物体所看到的形状是不一样的，并学会根据看到的形状正确地判断观察者的位置。具体而言，本节数学课程以发展学生空间观念为基础目标。由于低年级学生思维转化速度较慢，“体会从不同的角度观察物体所看到的形状可能不同”便成了教学难点。

在几何画板的运用中，教师可以“投影”的形式实施教学活动，以画板上的呈现画面让学生意识“观察角度”的问题。比如，在观察“粉笔盒”这一物品时，在传统教学中，教师为学生调整粉笔盒视角，让学生讲述自己看到的画面。实物学习虽然能快速调动学生的参与兴趣，但所获取的教育效果并不理想。学生能够说出不同角度看到的画面，但其对概念本质中的“观察视角”仍存在“一知半解”的情况。教师可利用几何画板中的投影功能，利用摄像头的观察视角，为学生展示“摄像头在粉笔盒左面、上面、正面、右面”的画面，并将各个画面呈现在黑板上。画板直观能促进学生观察细节。

通过图片与视角的差异，让学生讲述不同画面的差异及特点，以投影技术帮助学生理解“不同的角度观察物体所看到的形状可能不同”这一数学概念，同时也运用实践性教学活动激活学生对数学知识的兴趣，运用几何画板提高课上教育效能。

二、动态图像讲解，直观感知数学变化

几何画板在小学数学教学中的运用，打破了传统教学模式的局限性与死板性，相比较直观地观看图形、对比图形，几何画板从数量到图像上，让数学知识呈现了“动态化”的展现。因此，将几何画板应用于课堂教学，让学生观察图形的运动和变化过程，可以从中找寻变化中隐藏的“变”与“不变”，能让学生更直观地感知数学变化。基于几何画板的这一教学优势，教师需科学运用、合理分配，立足教学实际实施“动态图像讲解”，让学生更直观、清晰地感知数学变化，进而获取更为理想的教育效果。

在苏教版《义务教育教科书·数学》四年级上册中“垂线与平行线”一课第四课时的学习中，要求学生了解数学定义“垂线”，并掌握其概念“从直线外一点到这条直线所画的垂直线段的长度，叫作这点到直线的距离”。在本节课学习中，要求学生通过概念学习、图像观察，真正地理解垂线的出现过程，并认识与垂线的相关知识，基于实际生活能够对垂线的认识做出简单判断，最终促进发展空间观念的发展。由此可见，让学生学会“区分垂线”与“画垂线”，成为教学中的重点任务。

在几何画板的运用中，教师可基于所学内容为学生创设“动态化”讲解。比如，结合几何画板为学生展示动态教学图像，并结合图像向学生提出问题：“从点P 向已知直线画垂直的线段和几条不垂直的线段（如图1）。量一量所有画出的线段的长度及角度变化，你有什么发现？”

以动态化的图像作为讲解，让学生直观、形象地观察线段长度所产生的不同变化，并通过数据测量让学生发现，当“两条直线相交呈现90°直角时，点与线的距离最短”。在此基础上，教师便可引出“垂直”这一概念，引导学生画垂线、量垂线，以几何画板帮助学生积累图形学习的活动经验，掌握本节数学知识的核心概念，以直观形象的教学方法，让数学知识变得更加简单，更容易理解所学内容。

三、拆分计算内容，画板演示思维转化

前文提及，小学生思维发展阶段存在“具象化”的特点，对立体的、抽象的数学知识学习较为困难；高年级学生虽然思维处于“具体”向“抽象”的过渡阶段，但其思维转化能力仍然处于发展期，还无法直接将多项数学知识有效整合。通过对教材资源的解读，随着学生学习能力的提升，数学知识的学习难度也会越来越高，尤其在高年级数学学习中，“立体图形表面积”教学成为重点，需要让学生体会三维空间与二维平面之间的关系，并能利用已掌握的计算方式完成高阶学习。基于学科特点及学生发展实情，教师应立足教育实际，借助几何画板将数学知识“拆分”讲解，以画板的直观感知帮助学生完成思维转化，妥善完成数学学习任务。

在苏教版《义务教育教科书·数学》六年级下册中“圆柱和圆锥”一课中，第二课时学习以“圆柱的表面积”为重点教学内容，要求学生“理解圆柱的表面积的含义；探索并掌握圆柱侧面积、表面积的计算方法；会正确计算圆柱的侧面积和表面积”。本单元学习内容以“立体几何”学习为主，将锻炼学生的“三维空间”意识视为目标；但在“表面积”计算中，需要学生实现由“三维空间”向“二维平面”的转变。为帮助学生快速掌握“圆柱表面积”的计算，教师可利用几何画板，带领学生将“三维立体”拆分成“二维平面”，以直观的学习方式让学生掌握正确的计算方法，达成本课时教学目标。比如，教师可通过几何画板向学生出示“圆柱平面图（如图2）”：

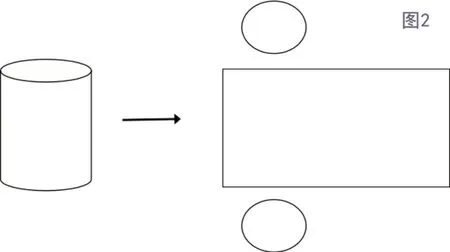
结合图像展开数学学习，让学生得知：圆柱的侧面积是一个“矩形”；圆柱的上面与底面，为两个“圆形”；两个底面的“长”是圆形的“周长”；矩形的“宽”就是圆柱的“高”等。通过几何画板的转化，帮助学生完成了思维由“三维立体”向“二维平面”的转化，学生了解到“圆柱的表面积=两个底面+侧面”。随后，教师便可引导学生结合数学经验引出学习问题，让学生将“S=πr2”与“S=a×b”公式融合，通过推理、简化计算出圆柱的表面积公式为“S=2πr(r+h)”。至此，在几何画板的有效运用下，学生直观、清晰地了解了圆柱体表面积计算方法及公式的演变过程，通过对知识点的“拆分”与“重组”促进学生数学思维的转化。

四、突破重点难点，提高数学教学质量

数学这门学科主要是研究客观世界中的数量关系以及一些或抽象或具体的空间形式。通常情况下，教师会将几何画板运用在“平面图形”或“立体几何”学习中，以使学生快速理解数学知识。随着几何画板深度开发，教师也可调整自身的教育思路，立足教育实际实现几何画板的多项运用，运用图像讲解帮助学生突破数学知识中的重点与难点，以进一步提升数学教学的质量。具体而言，几何画板还可运用在“数量计算”“空间方位”等学习中，教师要灵活转变教育思路，更好地发挥出几何画板的教育优势。

在苏教版《义务教育教科书·数学》四年级下册中“平移、旋转和对称轴”第二课时中，本节课基于学生三年级“认识旋转现象”基础之上开展的教学活动。详细解读第一课时教学，要求学生掌握“图形的旋转与旋转方向”两个关键要素，进而更好地了解图形旋转的特征，能根据图形旋转后的变化画出平移后的图形，以促进学生空间观念的发展。

基于所学内容，本课时学习的重点为：“通过观察、比较，掌握图形旋转的方法”；本课时学习难点为：“能在方格纸上将简单图形进行旋转”。随着教育目标的确定，为帮助学生快速理解“旋转”的概念，教师可利用几何画板实施教学活动。比如，在学习“三角形逆时针旋转90°”知识时，教师通过动态化图形演示，将“原图形位置”以“虚线”刻画出，并辅以“旋转箭头”向学生展示平移过程（如图3），让学生观察图像的发生的变化。在这一过程中，学生清晰观看到图片发生的变化，教师可提出问题：“三角形位置发生了什么变化？三角形围绕着哪一个做出了旋转？旋转的角度是多少？”等，通过图像、问题实施教育引导，巧用几何画板教育优势，帮助学生突破课程学习中的重难点，引导学生说出：“三角形一条直角边围绕着直角点逆时针旋转90°”，利用几何画板让学生更直观地了解“旋转”这一概念。在这一基础上，教师还可将“平移”知识融入其中，让学生讲述图像的平移过程，并在几何画板中标注图像平移轨迹，让学生更加直观了解数学概念，充分发挥几何画板的教育优势，促进数学课堂教育质量的提升。

在信息化时代的背景下，几何画板已经成为一项有效的教学辅助工具。小学生思维发展具有具象化的特点，几何画板中的各项功能，能帮助学生突破所学内容中的重点与难点。教师应加强对学习内容的调整，将数学知识与几何画板有效融合，不断提高学生对数学知识的兴趣，使其了解并掌握丰富的数学概念，让学生数学素养得到进一步提升。