小初数学衔接教学的思路与策略
2024-06-07仲秋月

【作者简介】仲秋月,高级教师,苏州市小学数学兼职教研员,江苏省教科研先进个人,苏州市“姑苏教育人才”,苏州市中小学数学学科带头人。
【基金项目】江苏省教育学会“十四五”教育科研规划重点课题“素养培育视角下‘数学+跨学科主题学习活动案例研究”(22B03SXSZ6);苏州市教育科学“十四五”規划2022年度课题“课程内容结构化:落实小学数学核心素养的实践与研究”(2022/LX/02/101/11)
【摘 要】当前,小初衔接问题已得到广泛关注,小初衔接过程中学生学习困难的原因不在于学习内容本身,而在于学生在小学阶段掌握的学习方法、形成的学习习惯已不再适应初中阶段的教学内容和教学形式。文章以几何思维水平进阶为例,讨论如何开展小初数学衔接教学,并提出了一些教学思路与策略,即基于小初数学衔接症结主动作为,分析小初数学学科素养衔接断层,建构小初几何思维水平进阶通道。
【关键词】小初衔接;数学教学;几何思维水平;核心素养
一、引言
《义务教育课程方案(2022年版)》提出,义务教育课程九年一贯设置,应注重学段衔接与科目分工,依据学生从小学到初中在认知、情感、社会性等方面的发展,把握课程深度、广度的变化,合理安排不同学段内容,体现学习目标的连续性和进阶性。[1]《义务教育数学课程标准(2022年版)》(以下简称《课标》)将九年的学习时间划分为四个学段,核心素养的表现体现在每个学段的具体目标之中,学段之间的内容相互联系,螺旋上升,体现了核心素养的整体性、一致性和阶段性。[2]可见,小学和初中阶段的数学课程是一个不能分割的整体,无论是学习内容、学习方法,还是素养要求,都具有延续性和连贯性。
二、小初数学衔接教学的困境与挑战
小初衔接阶段的学生正经历着身心发展的剧变。首先是生理发育加速,这个阶段的学生出现了生长期的又一个高值点;其次是思维从具体运算阶段开始进入形式运算阶段,信息加工能力明显增强。与此同时,他们的自我意识明显提升,与亲人、师长的关系从依赖走向独立。随着年龄增长、学段升高、环境变化,多数学生在小初衔接过程中会有不同程度的苦恼。据有关调查显示,41%的初中生在小初衔接阶段感到学科学习困难。而造成学段衔接问题的原因,51%的教师认为是上下学段教材、教学、管理等缺乏衔接,67%的教师认为是学生原有学习方法不适应新的教学内容、形式,31%的教师认为是教材和教师教法不科学,18%的教师认为是学生接受水平不适应教师的教学方法。[3]
(一)学生面临的学习挑战
对于数学学科,从内容来看,初中数学知识更趋向于抽象与理性,常识性知识相比小学明显减少,规律性、逻辑性知识明显增多;在逻辑思考方面,小学侧重于归纳推理,初中则逐步趋向于演绎推理;在问题解决方面,初中阶段更注重知识的综合运用与分析,对学生的数学阅读、分析问题和解决问题的能力提出了不小的挑战;在课堂容量方面,初中的数学课堂无论是呈现知识点的例题,还是作为巩固应用的习题,面更广、量更大,教师教学节奏加快。由以上可知,学生的数学学习方法必然随之而改变,学生需要具备一定的元认知和自我监控能力,需要更自觉、更独立、更主动地参与课堂学习,以理性、抽象的方式深入思考,以严谨的逻辑思维展开推理等。可见,小初数学衔接的关键在于学习方法上的衔接,而非学习内容上的衔接。
(二)衔接教学的现实困境
《课标》明确了各学段的课程内容、学业质量和课程实施等要求,但是小学和初中数学教师往往只关注自己所教学段相关的内容,缺乏整体把握素养目标和教学内容的意识,缺乏小初连贯一致的标准和评价方式,难以为学生搭建螺旋式上升的学习阶梯。与此同时,小学和初中教材缺乏一致性、连贯性的系统规划,两个学段的教师都只熟悉自己所教学段的教材。另外,小初分治的管理模式使得相关的小初衔接教学研究活动很少,教师得不到相应的培训,也没有机会对这一方面做更多的了解和研究。因而,教师普遍缺乏九年义务教育一致、整体和可持续发展的教育教学观,要让小初衔接工作从认知层面转向实践层面更是难上加难。
三、小初数学衔接教学的思路与策略
(一)亮观点:基于小初数学衔接症结主动作为
当前,学段衔接问题已得到广泛关注,如《国家中长期教育改革和发展规划纲要(2010—2020年)》强调人才培养体制改革要树立系统培养观念,推进大中小学有机衔接。教育部《关于全面深化课程改革落实立德树人根本任务的意见》也指出高校、中小学课程目标有机衔接不够的问题,并提出了解决办法、要求和目标。然而,大多数教师、家长和学生对于小初衔接的理解比较粗浅,认为小初衔接的症结在于学习内容和知识难度的增加。因此,在小学升入初中的暑假期间,很多家长和学生选择“小初衔接班”提前学习,以一种“抢跑”的方式,试图缓冲小初衔接过程中带来的问题。
实际上,学生在跨学段学习过程中产生的明显学习障碍导致的学习成绩下滑的根本原因并不在于学习内容本身,而在于学生在小学阶段掌握的学习方法、形成的学习习惯已不再适应初中阶段的教学内容和教学形式。调查显示,小初衔接阶段的初中生感到学习困难的原因,有48%表示不知道该怎么学,有32%表示知识难、听不懂,有25%觉得教师教法不适应。
由此可见,教师要做的小初衔接教学并不是知识内容层面的衔接,而是学习方式、认知心理上的衔接。小初衔接阶段的学习困难问题虽然发生在初中刚入学时,但为了让学生能够平滑且顺畅地度过衔接期,教师应尽可能减缓衔接的坡度,拉长衔接的过程。小学教师应该主动作为,从五、六年级开始有意识地与初中教学进行对接,而不是让学生在初中入学后发生问题时,再由初中教师来面对衔接问题。首先,小学高学段数学教师应走进初中数学课堂,了解小学高年级学生在思维方式、思维能力、学习习惯等方面和初中起始阶段的要求存在的差异和断层,从而树立衔接意识,重视衔接教育。其次,小学教师也要研究初中数学课程标准和教材,把握教材体系中的连接点,了解学习内容上的盲点、断点和交叉点,从而对接学科知识,整合课程内容。再次,小初数学教师要开展跨学段教学研究活动,研讨小初数学教学的特点,共同面对小初衔接问题,展示各自的课堂教学,交流教学方法,搭建衔接台阶。最后,小学数学教师要根据小初衔接阶段学生数学思维发展的特点,设计衔接课程,把握当下知识的生长点,看到知识的发展点,在小学高年级阶段适当延伸教学内容,拓展学生的数学思维,提高学生的自主学习能力,为学生的初中数学学习搭桥铺路。
(二)寻锚点:分析小初数学学科素养衔接断层
教师应尊重学科知识的内在逻辑体系要求,尊重学生学习心理发展的内在需求,把握小初教材体系的内在联系,梳理结构与内容,找到小初数学学科知识和学习方法的衔接点、断层点,为教学的科学过渡铺设平缓坡道,让学生在衔接区尝试感受新的学习方式,实现学科逻辑与学生心理逻辑的统一。本文以几何思维水平进阶为例,阐述这一观点。
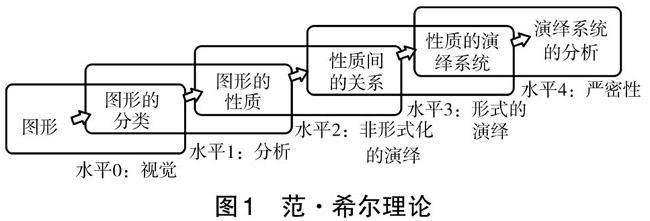
学生的几何思维水平需要不断地通过一系列有意义的活动来获得。范·希尔理论是用于理解学生空间观念的层级体系(如图1)[4]。
对照《课标》学业质量标准要求,我们可以发现,第三学段(五、六年级)要求学生能认识常见的立体图形和平面图形,计算图形的周长、面积(或表面积)、体积,能描述图形的位置和运动,形成量感、空间观念和几何直观;第四学段(初中阶段)要求学生知道运动过程中的不变量、图形运动的变化特征,能运用几何图形的基本性质进行推理证明,初步掌握几何证明方法,进一步增强几何直观、空间观念和推理能力。可见,五、六年级的学生已经认识了常见的立体图形和平面图形,并能够根据其性质将图形分类,建立起其中的种属关系,即达到了几何思维水平1(分析),他们的几何思维也开始向着水平2(非形式化的演绎)发展,即学生从了解图形的性质逐渐转向探索图形之间的性质关系。
有研究表明,七年级学生的几何思维水平分布差异性较大,有81.37%的学生几何思维水平处于水平1,也就是说大部分学生依然处在感官学习图形的水平上,只有16.67%的学生几何思维水平达到水平2,这部分学生能从图形性质的角度把握图形。[5]然而,七年级教材中水平2的知识点急剧增加,根据范·希尔几何思维理论的不适配性,此时“教”与“学”的几何思维水平产生较大落差,学生很难理解教师的讲解内容,从而产生学习困难。可见,在“图形与几何”领域,小初衔接阶段的衔接锚点在于建立图形之间的性质关系,夯实小学阶段几何基础知识,深化知识理解,建立结构化知识体系,从而帮助学生实现从水平1到水平2的进阶,缩小差距,连接断层。
(三)接断点:建构小初几何思维水平进阶通道
小初衔接阶段的数学教师应锚定小初衔接断层,对接初一的教学要求与模式,思考“教什么”“怎么教”以及“教到什么程度”这三个问题。另外,通过学习内容的深化、学习方式的活化和知识体系的结构化,打通小初数学学科素养进阶通道,连接断点,形成一种更为适合初中学生学习的认知方式,改善学生的学习心理,帮助学生科学衔接、平缓过渡。
1.深化:建构知识关联的进阶通道
“教什么”是小初衔接教学的核心问题。小学和初中数学在“图形与几何”领域的学习内容不同,但有着紧密的联系,小学的学习内容是初中的基础,初中的学习内容是小学的延伸。数学教师应首先对小学和初中数学的相关知识进行梳理和比照,深入几何知识本质,建立小初知识之间的关联,以“递进”或“补充”等多样化方式确定衔接内容,导向知识生长方向,帮助学生在小学阶段就走好小初进阶的第一步。
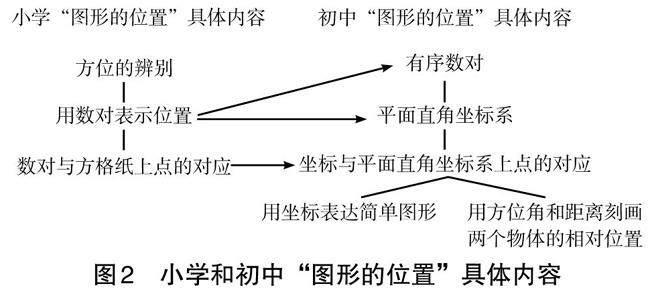
比如,对于“图形与几何”领域的“图形的位置”内容,我们很容易梳理出小学和初中的具体内容与内在联系(如图2)。
平面直角坐标系是沟通代数与几何的桥梁,小学阶段所学的用数对表示位置是用坐标表示平面上点的位置的雏形。学生在认识数对时,常常不理解为何数对中要将列写在前,而将行写在后,只能靠死记硬背记住这一规则。事实上,这是与平面直角坐标系中的横、纵坐标相关联的。教师在深入理解这一几何知识本质后,就应当在小初衔接阶段提前引入平面直角坐标系,让学生理解坐标的意义。学生通过对图形位置与运动的观察和表达,体会坐标表达的重要性,为初中学习数形结合奠定基础。由此,通过小初数学教学内容的比较和关联,教师能够更好地把握数学知识的来龙去脉,以更高位的课程观设计教学,通过揭示知识本质引领学生进行有意义的深度学习。
2.活化:建构学法转换的进阶通道
小学阶段侧重于直观几何、实验几何,要求学生通过观察、操作、探索等亲身经历的活动,认识图形的特征与性质,发现图形性质之间的关系。初中阶段则侧重于论证几何,要求学生通过观察、发现、猜想、说理和论证等过程,逐步实现围绕性质的逻辑论证。小初衔接阶段,学生的几何思维水平正由水平1(分析)向水平2(非形式化的演绎)进阶。此时,学生已经认识了一些常见的平面图形和立体图形,了解了一些图形的性质特征,比如三角形的特征与分类等。反观初中数学课程内容,同样是这些图形,但要求学生深入探索图形之间的性质关系和图形性质之间的联系,比如三角形的内角和定理、勾股定理等。因此,除学习内容上的深化关联外,教师更应注重学生学习方法的转换,适时渗透论证几何的逻辑演绎方法,让合情推理与演绎推理并行,打开学法转换的通道,促进学生几何思维水平进阶。比如,学生在小学的学习中已经知道“三角形的内角和为180°”这一事实。对于这一图形性质,小学生是通过用量角器测量三个角的度数并算出总和,以及将一个三角形的三个角剪下并拼成一个平角等测量、操作、运算的方法发现的,而这一性质在初中阶段需要通过作一条与三角形某一边平行的辅助线进行严格证明。
因此,在小初衔接阶段,教师就应在学生原有的认知基础上进行适当的拓展和深化。教师可以准备三个完全相同的三角形,相同的角標上类似的序号,并引导学生将三角形的三个角拼在一起(如图3)。在学生发现三角形的三个角拼成了一个平角后,教师引导学生思考:“你能在这幅图中找到几组平行线?能找到平行线中相等的角吗?”当学生直观认识了平行线间同位角相等、内错角相等之后,很容易借助一组平行线来证明三角形的内角和是180°(如图4)。如此,学生就能够从直观几何、实验几何向着演绎推理、论证几何前进一小步,也能初步了解初中阶段几何知识的学习方法,感受学习方法的转换,做好学习心理准备,缓解衔接焦虑。
3.结构化:建构认知系统的进阶通道
小学数学中“图形与几何”领域的教学内容分散在一至六年级的教材中。学生在各年级的学习中所获得的认识不仅缺乏整体性和系统性,而且由于相关知识经验和认知水平的局限,他们对很多知识的理解往往还比较直观,存在诸多认识上的困惑甚至盲点。因此,小学阶段学生对于图形性质之间的联系不是十分明确,常常“只见树木不见森林”,这在很大程度上影响了学生几何思维水平从水平1过渡到水平2,即从了解图形的性质,逐渐转向探索图形之间的性质关系和图形性质之间的联系。而对知识结构的透彻理解能够缩小“高级”知识和“初级”知识之间的间隙,为知识的衔接提供良好的过渡条件。小初衔接阶段,教师应引导学生基于知识自身的发展逻辑,梳理并建构知识结构,掌握图形性质及其关系,进而为几何思维水平的進阶提供可能。初中数学教材中,涉及小学已学的知识一般不再重复学习,而是直接在例题或习题中加以运用。因此,小初衔接阶段,教师应从“数学化”角度出发,重视横向与纵向的关系,帮助学生把已经学过的几何图形知识点进行整合,发现共同规律,建构相对完善的知识与方法体系,必要时适当引入初中阶段的上位概念,促进学生对原先浅层次的几何知识的再认识,为后续的学习提供思考导向。
比如,在“图形与几何”内容学习中,教师引导学生对“立体图形”进行了结构化梳理(如图5)。学生不仅逐个分析了这些学过的立体图形的特征、表面积和体积的计算方法,而且进一步发现了图形性质之间的联系。如长方体的长、宽、高相同时就成了正方体,因此,正方体是特殊的长方体。再如,长方体、正方体和圆柱的体积公式虽然不同,但通过回顾这些立体图形体积公式的推导过程,得出上下一样粗的柱体的体积都可以运用V=Sh这个公式,等等。如此,在回顾知识的本源中实现意义的沟通、运用的拓展,有效扩张知识结构网的容纳度,提高学生的几何思维水平。
综上所述,小学数学教师需要“瞻前顾后”,准确定位当下的教学,同时“遥望”初中数学,为学生数学学习的下一站铺一段、渡一程,巧妙地解决小初衔接不畅的现实问题。本文基于范·希尔理论,主要讨论了“图形与几何”领域的衔接问题。事实上,以上理念与策略同样适用于小初数学衔接的其他领域。
参考文献:
[1]中华人民共和国教育部. 义务教育课程方案(2022年版)[M]. 北京:北京师范大学出版社,2022.
[2]中华人民共和国教育部. 义务教育数学课程标准(2022年版)[M]. 北京:北京师范大学出版社,2022.
[3]王言锋,王睿,薛晓光,等. 基础教育学段衔接问题调查报告[J]. 大连教育学院学报,2016(3):53-56.
[4]范德沃尔,卡普,贝-威廉姆斯. 美国中小学数学教学实践手册[M]. 10版. 张晶,侯慧颖,施银燕,等译. 上海:华东师范大学出版社,2023.
[5]曹晖. 中小学数学“图形与几何”教材内容衔接分析[D]. 海口:海南师范大学,2015.
(责任编辑:罗小荧)
