探究平面几何证明思路的思维过程
2024-06-07张昆


【作者简介】张昆,博士,副教授,中学高级教师。主要研究方向为数学教学论、数学史、数学教师教育、数学教育哲学。
【摘 要】本文通过“边想边说”与反思相结合的研究,发現在探究平面几何证明思路时,学生的思维存在三个层次,其中思维的第二层次具有非常高的教学价值;一个班级中的学生存在着不同的认知方式,学生个体一般以自己的优势认知方式理解情境中的信息,从而赋予信息以意义。因此,在探究平面几何证明思路时,教师应通过教材分析与学情分析,选择具体的思维层次的几何证明题,平衡学生需要的认知方式,做好教学设计及课堂实施活动。
【关键词】探究;思维过程;思维层次;平面几何;“边想边说”;反思
开篇明义,本文要研究学生探究平面几何证明题时的思维活动过程。那么,什么是数学思维呢?所谓数学思维,指的是在遇到数学情境、学习数学知识或解决数学问题时,学生为了应对其中的困境,他们的认知结构中所发生的心理活动。[1]这就将数学思维界定为一种狭义的个性心理活动,依据这一数学思维内涵,可以将数学思维过程界定为处理数学符号元素及符号元素之间互相作用的心理活动过程。[2]数学符号元素包括数学意象、数学概念和表示具体数学内容的语言(如汉语、英语等)、图形、图表等,数学符号元素及其互相作用是学习主体能够调动、调整、控制甚至临时自行创造出来的。
为了研究学生探究平面几何证明思路的思维过程,以下先讨论由数学思维及思维过程的内涵所决定的个体数学思维的三个主要层次。
一、学生探究平面几何的思维层次
为了探究数学思维活动操作的心理过程,首先从对思维及其结构的譬喻展开认知。众所周知,当人们在一件乐器上弹奏一个音时,在这件乐器可能发出的全部声音中,只有这唯一的一个乐键发出来的那个音是现实的。同样,当人在感知眼前的事物时,他规定的全部无限可能性就被限制在这唯一的存在方式上。因此,在只有这种冲动发生作用的地方,必然存在着最高程度的限制;人在这种状态中只不过是一个数量的统一体,是时间的一个实现了的瞬间。[3]
由这个譬喻内容可以认识到,大脑中存在的思维瞬间相当于一件乐器上的一个按键,发动思维活动的某些物质性的要素,也会组成一个结构,我们将其简称为思维结构。因此,这里要考察探究平面几何证明思路所需要动用的思维结构。由数学思维与数学思维过程这两个概念所界定的内涵可以认识到,面对具体的数学问题,学生在应对问题所提供的具体信息时,会启动思维并维持思维进展,这是大脑作为整体结构所支持的一种产生思维活动的思维结构。这种数学思维结构的构成成分,应该存在从具体逐步到抽象的三个主要层次。
1.第一层次
第一层次,具体数学问题中涉及的引发学生利用知识、方法等辅助思维的材料被立即激活。此时,对于探究某一具体的平面几何证明思路,学生会审视问题信息的特点、已掌握的平面几何知识内容(包括几何概念、公理、定理、性质等)、数理逻辑(外在表现为问题信息中的因果关系,这种因果关系可内化为大脑中的相关对应物,如排序、包含、点数、空间等形式)[4]、所需要的证据(由几何概念、公理、定理等已掌握的知识提供)、过去探究解题的方法与经验等,这些都会对学生的探究思路起到启发性作用,整个思维活动及过程都受到学生个体经验中的这些要素的有价值的指导。
学生所掌握的平面几何知识、方法、经验、符号(或语言)等,为解决具体的平面几何问题而展开的探究证明活动提供了启发(如分析法与综合法启发证明思路),从而启动思维,形成思维的定向,即思维活动的导向性轨迹等。这种导向性轨迹对于学生萌生有价值的证明思路具有非常重要的作用,也存在着学生个性数学思维的适应性(配合外在条件信息)的应用价值。因此,这种探究思路过程的思维是一种可观察、可体悟的明晰的活动过程,思维的第一层次构成探究平面几何证明思路的基础性依靠。
2.第二层次
第二层次,相对于某个学生而言,面对平面几何证明题的问题信息时,在思维的第一层次的某个或某几个思维环节,利用已掌握与积累起来的知识、方法与经验等处理数学符号(如几何图形,表示图形的语言)元素及符号元素之间所应该构成的关系时,难以达到具体目的,也就是依据这些元素学生无法形成清晰的思维轨迹。学生对于这道平面几何证明题所提供的外在信息(数学符号元素之间)只能进行外在现象的偶然搭配,探究有可能构成有意义(也有可能无意义)的轮廓结构。如此,学生处于认识的无目标、无顺序之中。
思维的第二层次处于一种中间状态。思维的第一层次的特点在于,学生能够在充足的时间内自己探究出至少一条具体的证明思路,即能够比较顺利地从具体证明题的题设条件过渡到题断结论。思维的第二层次的特点在于,学生在探究证明题的思路时不是一帆风顺的,而是在从题设条件到题断结论的某些环节上需要发掘隐含条件(不能通过仅观察原问题的信息就能一眼看出的条件),需要在某个环节中架设起桥梁才能形成清晰的思维轨迹。
思维的第二层次应该是需要教师最为关注的地方。这是因为学生在教师精心的教学设计和课堂实施的启发下,历经艰难的思考活动,至少从体验上感受到,经由自己思维力量(主体精神)的发挥,能在疑难环节上架设起证明思路所需要的桥梁。这是教师应该十分关注的地方,因为平面几何证明题的教育教学价值主要体现在这些疑难环节上:一方面,这些疑难环节是教师培养学生思维能力的优质的教学素材,是学生能切身理解与体会的疑难所在,学习时具有极强的针对性;另一方面,当学生在教师的启发下真真切切地突破了疑难环节,他们的学习情感就会得到极大的满足,体会到思维活动的巨大潜力,如此,在面临新问题时就会更集中注意力,维持思维就会更具持久性,力图独立完成探究活动的任务。
3.第三层次
第三层次,有的学生可能没有完全理解题目提供的条件或结论所代表的具体意义,因此思维活动可能具有漫然性特点,对于问题所提供的条件或结论无法触及。这种思维可能是从条件或结论的细枝末节中找到一种似是而非的支点,导致结果可能脱离条件或结论的本质信息,远离题设条件或题断结论的具体现实情境,更偏向于学生主观的情感、想象。因此,这种思维无法获得需要的结果。
即使如此,教师在教学设计及课堂实施中,对于思维的第三层次,也应该本着“取其精华、去其糟粕”的原则。在探究平面几何证明思路时,教师在启发学生的思维活动中必须处理好“虚”与“实”之间的关系。教师要认识到,思维的第三层次(思维已经处于比较“虚”的状态)对于发展学生思维的创造性具有非常重要的作用,因为思维的创造性发挥可以帮助学生萌生重要的观念。这种比较“虚”的思维活动虽然可能完全不顾及题目所设定的情境事实,但是在某种意义上依然存在思维对于问题信息的现实的适应性,从而引发学生对于题目所设定的现实产生一连串的思维活动,使得探究证明思路取得实际成效,特别是为突破疑难环节时所需要的创造性发挥提供精神“养料”。教师应该认识到教学要帮助学生体验从“虚”到“实”的思维活动转化过程。
4.思维三个层次的关系
基于以上分析,教师在教学设计及课堂实施时,需要特别关注第二层次的思维活动:在思维的第一层次中,即使没有教师的教学启发作用,学生也能按部就班或早或迟地找出证明的思路;思维的第二层次出现时,学生已经完成了思维的第一层次的探究活动并出现了疑难环节,因此教师需要引导学生突破疑难环节,将这些疑难环节转化为优质的教学资源,引发学生的创造性思考,进一步发掘问题中的隐含条件。学生的思维能力在第二层次“真刀实枪”的思维活动过程中能更好地发展起来。
突破疑难环节的创造性思考,离不开第三层次思维的支持。当学生在客观上设定的解题目标与探究解题思路处境中的某些环节之间存在鸿沟,学生经由不断努力还是难以架设起桥梁时,就体会到过去习得的解题经验与方法对于目前面临的新问题无济于事,这就使得学生的思考活动处于停滞状态。此时,需要一些离问题情境较远的自由想法,这些自由的想法中可能会有解决当前疑难问题的有价值的思维成果。思维的第三层次的作用就在于此。
总之,思维的三个层次具有互相作用的关系,因此,教师在教学设计及课堂实施中,应该以思维的第一层次为基础,以思维的第二层次为教学重点与突破口,以思维的第三层次为创新活动的出发点,在备课时通过各个侧面进入教学活动过程,尽可能多地找到解题途径,仔细分析学生的思维水平与状态,提高数学课堂教学的有效性。
二、学生实际思维活动过程
“边想边说”的研究方法虽然是一个研究学生数学解题思维活动的好方法,但这种方法也存在缺陷。因为从启动与维持思维活动的本质上看,探究平面几何证明思路所发起的绝大部分思维活动(特别是创造性想法的出现)是无意识的,所以尽管研究者想要学生说出真实的思考过程,但在某些思维的关键节点上往往难以实现。此时,就需要对学生突破疑难环节的成熟的思维活动过程进行反思,试图从其所经历的思维体验中追溯过去实施的思维活动过程。
现举一例来说明“边想边说”与反思相结合的方法,探究学生关于某一道平面几何证明题思路的思维活动过程。
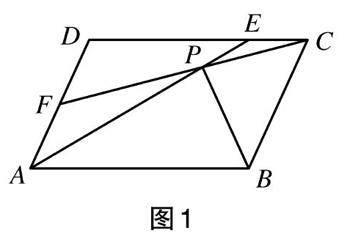
例1 已知:如图1,在[?ABCD]中,AE=CF,AE与CF相交于点P,连接PB。求证:∠BPA=∠BPC。
師:记AE=CF为条件式①,∠BPA=∠BPC为结论式②,那么,如何探究证明结论式②的证明思路呢?
生1:在[?ABCD]这个框架中,条件式①没有什么特别的,结论式②说明了线段BP是∠APC的平分线。要证明一条射线是一个角的平分线,可想到“到角的两边距离相等的点在这个角平分线上”这个定理。于是,过点B分别作BM⊥AE③交AE于点M,作BN⊥FC④交FC于点N(如图2所示),现在证明BM=BN⑤这个过渡性的中间结论就能达到目的了。我想到证明Rt△BPM
【说明】从例子中学生“边想边说”的内容可以看到,学生目前处于思维的第一层次,即从题断结论出发,将所要证明的结论式②转化为证明过渡性结论式⑤。但是他遇到了第一个疑难环节,这就需要他发掘题意中的某些隐含条件来突破这个疑难环节,这道题的证明思路才能打通。
师:你想得很不错了。你开头就提出了“在[?ABCD]这个框架中”,说明在你的意识中存在希望将条件与结论构成整体性的心理意向。你认为这道题的条件式①是肯定成立的,所需要证明的过渡性结论式⑤也一定成立。那么,①与⑤在[?ABCD]这个框架中可以构成一个有意义的整体吗?
生2:我感觉不到①与⑤如何才能构成一个有意义的整体……
师:仔细对照图2,你能猜想出①②③④这些要素如何组成一个有意的轮廓吗?
生3:我观察图2这个图形,注意力逐渐集中于[?ABCD]这个框架中的条件BM⊥AE③与条件BN⊥FC④上,发现线段AB、线段AE和垂线段BM这三者之间没有构成以一种有价值的轮廓(完整图形的结构——笔者补充)。因此,我想到连接线段BE(如图3所示),于是知道了线段BM是△AEB底边AE上的高,因此,AE·BM=2S△BAE,而2S△BAE=[S?ABCD]⑥;同理,连接线段BF,可以得到CF·BN=2S△BCF=[S?ABCD]⑦。由等式⑥与等式⑦,知道等式AE·BM=CF·BN⑧成立,由条件式AE=CF①知过渡结论式BM=BN⑤成立,于是所要证明的结论式∠BPA=∠BPC②成立。
生4:因为①与⑤应该同时成立,现在我想将①与⑤集中起来构成一个整体性条件。集中的途径是将①与⑤中的左右两边的两条线段分别进行加减乘除运算,可以得到四个相关线段运算的等式,即AE+BM=CF+BN,AE-BM=CF-BN,AE·BM=CF·BN⑧,[AEBM]=[CFBN]。在这四个等式中,通过赋予其意义加以考察,由条件BM⊥AE③与条件BN⊥FC④,发现可以赋予等式⑧这个乘积式以三角形面积表达式的意义,其他三个等式都无法赋予意义。于是,将等式⑧两边都乘[12],知等式[12]AE·BM=[12]CF·BN⑨应该成立。[5](后续内容与生3类似,不再赘述。)
【说明】生3与生4在探究这道证明题时,使用了不同的思维方式。生3偏向于图形直观,由所作辅助线呈现的状态直接看出可以利用三角形面积公式,而生4则偏向于运用已知条件或证明结论之间的关系所生成的集中条件的观念,利用运算得到结果。
由“边想边说”与反思相结合的研究方法可以发现,在探究平面几何证明思路时,学生的思维存在着三个层次,其中思维的第二层次具有非常高的教学价值。与此同时,一个班级中的学生存在着不同的认知方式,学生一般以自己的优势认知方式理解情境中的信息,并赋予信息以意义。因此,在探究平面几何证明思路时,教师应该通过教材分析与学情分析,选择具体的思维层次(最为重要的是思维的第二层次)的几何证明题,平衡学生需要的认知方式,做好教学设计及课堂实施活动。
参考文献:
[1]张乃达. 数学思维教育学[M]. 南京:江苏教育出版社,1990:4.
[2]克雷奇,克拉奇菲尔德,利维森,等. 心理学纲要:上册[M]. 周先庚,林传鼎,张述祖,等译. 北京:文化教育出版社,1980:188.
[3]席勒. 审美教育书简[M]. 张玉能,译. 南京:译林出版社,2012:35.
[4]皮亚杰,英海尔德. 儿童心理学[M]. 吴福元,译. 北京:商务印书馆,1980:7.
[5]张昆,曹一鸣.完善数学教师教学行为的实现途径[J]. 数学教育学报,2015(1):33-37.
(责任编辑:潘安)
