摩擦驱动焊接小车牵引力和通过性分析

张建军，黄继强，薛龙，李茂勇，张瑞英

（北京石油化工学院，北京 102617）

0 前言

相比于常规的工业机器人，带轨道的焊接小车因为拆装方便、重量轻等特点，更方便实现野外环境下的自动化焊接[1-2]。但是，焊接小车因配合轨道限制，只能针对固定外形的工件进行焊接，多为曲率半径恒定的管件或者板件，难以适用于曲率半径变化的工件，限制了焊接小车的适用性[3-4]，提高了生产成本。许多研究人员致力于突破焊接小车的这一困境，蒋骁骊等人[5]提出了一种全位置管道焊接小车，可以适配多种规格的轨道，实现对不同管径管道的焊接，但是针对变曲率半径的工件仍然无能为力。出现这种问题的原因在于曲率半径变化较大的工件需要根据工件形状定制轨道，而传统的焊接小车通过齿轮齿条进行传动，当轨道的曲率半径突然变化时，齿轮齿条之间啮合困难，无法保证焊接小车的平稳运行[6]。

摩擦驱动方式不受齿轮传动啮合的影响，对变曲率半径轨道具有较好的适应性[7-8]。为此，采用摩擦驱动方式，设计了一种可与变曲率半径轨道相配合的焊接小车，并对其牵引力和通过性进行分析[9-10]。最后经过仿真验证，证明该焊接小车在变曲率半径轨道上具有较好的通过性，满足复杂曲面工件的自动化焊接需求。

1 焊接小车牵引力分析

如图1 所示，所设计的焊接小车主要由行走胶轮、夹紧轮、凸轮夹紧机构、车体等构成，自主设计的凸轮夹紧机构和夹紧轮相互配合，使焊接小车的行走机构具备更好的适应性。在轨道的曲率半径发生变化时，凸轮夹紧机构在轨道摩擦力的驱动下，沿行走胶轮的轴向转动，保证焊接小车的行走胶轮不会因为阻力的变化发生滑动。

图1 焊接小车组成示意图

摩擦驱动的焊接小车在变曲率半径轨道上行驶时，会经历各种复杂的工况，为保障焊接小车的平稳运行，对焊接小车在不同工况下的牵引力进行分析，以确定其在不同位置的牵引力变化规律，为后续驱动装置设计提供参考。

焊接小车运动过程中，其行走胶轮与轨道的接触面均可近似看作斜坡面，匀速运动时，夹紧轮、行走胶轮、夹紧机构可以看做整体进行分析。以轨道坡度角为 α时焊接小车的运动状态为研究对象，假设焊接小车以速度v做爬坡运动，胶轮与轨道接触面摩擦系数为 µ1，胶轮半径为r1。焊接小车在斜坡工况下的受力分析如图2 所示。

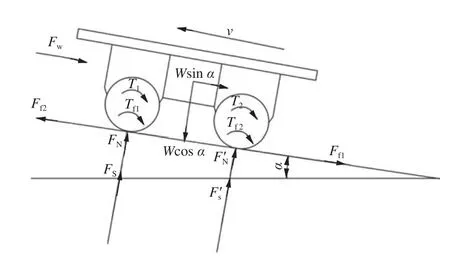
图2 焊接小车整体受力分析示意图

图2 中W为车体重力；Fw为空气阻力；Ff1，Ff2为作用在主动轮、从动轮上的摩擦力；Tf1，Tf2为作用在主动轮、从动轮上的滚动阻力偶矩；T1，T2为作用在主动轮、从动轮上的惯性力偶矩；FN，FN′为主动轮、从动轮支持力；Fs，Fs′为主动轮、从动轮夹紧力；α为斜坡倾斜角度；v为运动速度。

图3 为焊接小车行走胶轮受力分析示意图，图中G为 行走胶 轮重力；Tt为驱动 力矩；Fz1，Fz2为车体 作用于主动轮、从动轮的压力；Fp1，Fp2为驱动、从动轴作用于主动轮、从动轮的平行于路面的力。

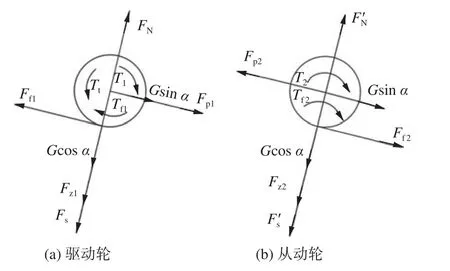
图3 焊接小车行走胶轮受力分析示意图

如图3 所示，通过隔离法对焊接小车行走胶轮进行受力分析，由焊接小车从动轮的转矩平衡条件，得

式中：r为焊接小车从动轮半径。

图4 为焊接小车车体受力分析示意图，Fzw1，Fzw2为车体受到主动轮、从动轮的支持力。

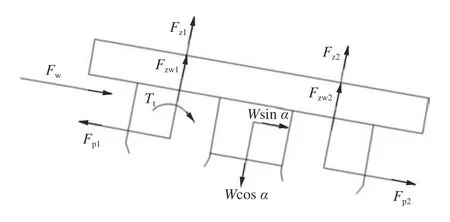
图4 焊接小车车体受力分析示意图

焊接小车车体进行受力分析如图4 所示，车体的径向力平衡条件为

由式（1）、式（2）计算得到Fp1为

假设焊接小车的行走胶轮均匀受力，则车体对从动轮的压力为，从动轮受到的滚动摩擦力Ff2为

式中：µ1为滚动摩擦系数。

实际焊接作业时，焊接小车的空气阻力和惯性阻力偶矩值较小，可以忽略不计，则式（3）可简化为

焊接小车在变曲率轨道上作业时，会经历平焊、立焊、仰焊等多种位置，因此，以焊接小车在斜坡工况下的牵引力变化规律为基础，研究焊接小车在平焊工况、立焊工况和仰焊工况下的牵引力对保障其适用性具有重要意义,下面分别进行讨论。

式（4）中当 α=0时，相当于焊接小车进行平焊作业，此时焊接小车的牵引力为

当 α=π/2时，相当于焊接小车进行立焊作业，此时焊接小车的牵引力为

当 α=π时，相对于焊接小车处于仰焊位置，此时焊接小车的牵引力为

仰焊位置时，焊接小车倒挂在轨道上，夹紧轮承担焊接小车的重力荷载，由式中可以看出此时夹紧轮与行走胶轮支持力的合力方向与夹紧力的方向相反。

综上所述，焊接小车在变曲率轨道上运动时，为保证焊接速度恒定，其牵引力应处于动态变化过程中。焊接小车在平焊位置、立焊位置、仰位置处的牵引力计算公式分别如式（6）、式（7）、式（8）所示，由于小车的重力远大于摩擦力，因此可以看出，在仰焊位置处所需的牵引力最大，可以以此作为电机选型的依据。

2 通过性分析

摩擦驱动的焊接小车克服了齿轮啮合传动方式难以适应不同曲率半径工件的问题，但因为受到车身尺寸、轮距等因素的影响，对不同曲率半径工件也存在一定的适应范围，因此对焊接小车的通过性进行分析，为焊接小车的结构尺寸设计提供依据。如图5 所示，在焊接小车处于曲面轨道的内凹侧和外凸侧位置时，其通过性有较大差异，下面分别予以讨论。

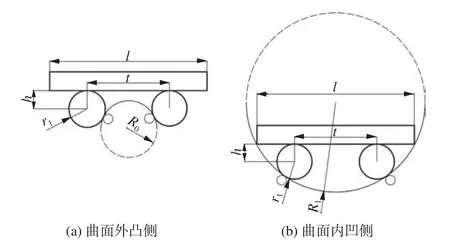
图5 焊接小车所处位置

图5 中R0为焊接小车可通过的轨道最小半径；h为行走胶轮轴心与底盘距离；t驱动轮与从动轮的轴心距；l为焊接小车长度；r1为行走胶轮半径。

焊接小车处于曲面轨道的外凸侧时，受到焊接小车结构尺寸的影响，此时，焊接小车可通过的轨道最小半径为

此时，焊接小车的最小离地间隙为0，如果轨道曲率半径进一步减小，焊接小车将无法通过，即焊接小车处于曲面轨道的外凸侧时，可通过的轨道半径应大于R0。

焊接小车处于曲面轨道的内凹侧时，当轨道的半径过小时，焊接小车会因为自身尺寸的限制与轨道发生碰撞，假设R1为焊接小车可通过的轨道最小半径，经计算

其中：

此时焊接小车的接近角和离去角为0，即焊接小车处于曲面轨道的内凹侧时，可通过的轨道半径应大于R1时。

综上所述，焊接小车的通过性与焊接小车的结构尺寸有关，焊接小车的结构设计越紧凑，行走胶轮半径越小，其在轨道上通过性越好，因此，在对焊接小车的结构进行设计时，需要根据式（11）、式（12）进行计算，保证轨道的所有外凸侧曲率半径均大于R0，内凹侧曲率半径均大于R1。

3 仿真验证

根据上述分析结果，研制了一款摩擦驱动的焊接小车，具体尺寸为：外边缘长度l=250 mm，胶轮横向轴心距t=130 mm，胶轮半径r1=28 mm，胶轮轴心与底盘距离h=45 mm 。小车车体质量m=15 kg，胶轮质量mb=0.1 kg，胶轮与轨道接触面的摩擦系数为µ1=0.5，从动轮夹紧力。

焊接小车在曲面轨道上运动时，由于运动速度较慢，可以忽略向心力的影响，根据前述牵引力分析给出的牵引力计算公式，通过Matlab 软件绘制出焊接小车牵引力F和斜坡倾角 α之间的函数关系如图6 所示。

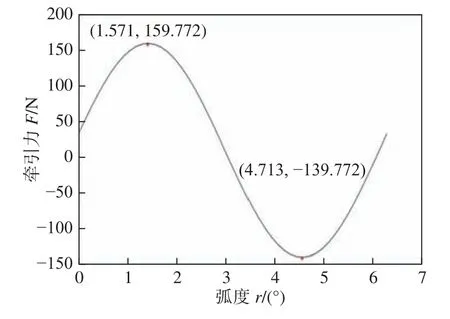
图6 焊接小车牵引力变化曲线图

可以看出，焊接小车牵引力的变化规律呈正弦函数变化，在立焊位置处，焊接小车的牵引力最大，最大牵引力Fpa=159.772 N，与前述牵引力分析中得到的结论一致。通过计算，可以得到驱动电机最大扭矩为1.2 N·m，因此，焊接小车驱动装置选用型号为57BYG250C-8 的普菲德57 电机，转矩为1.8 N。

根据前述通过性分析，将焊接小车尺寸数据代入式（11）、式（12）得 到，R0=37.4 mm，R1=129.2 mm，即理论上焊接小车可以通过半径R＞37.4 mm的外圆轨道和半径R＞129.2 mm的内圆轨道。为了对其通过性进行验证，以R0和R1分别作为轨道外凸侧和内凹测的曲率半径，构建了如图7 所示焊接小车在变曲率半径轨道上的运动仿真模型，通过Solidworks 软件对焊接小车在变曲率轨道上的运动过程进行仿真，设置小车经过0.6 s 的加速后，以v=10 mm/s的速度进行匀速运动，得到焊接小车在变曲率半径轨道上的运动速度仿真曲线如图8 所示。

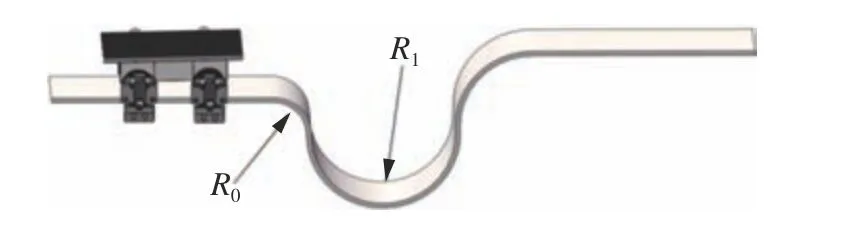
图7 运动仿真模型

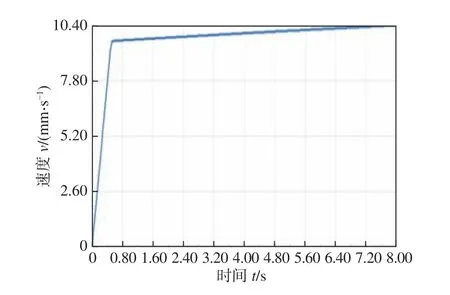
图8 速度仿真曲线

由图8 可以看出，焊接小车在经过0.6 s 左右的加速时间后进行匀速运动，整个运动过程中焊接小车的速度-时间曲线呈连续性变化，没有出现不连续问题，说明所设计的焊接小车可以顺利通过设定的变曲率半径轨道，满足设计的通过性要求。

采用外径 ϕ130 mm 的圆形轨道对研制的焊接小车进行通过性测试，根据仿真结果对运动过程中的牵引力进行设定，焊接小车顺利通过了圆形轨道，测试结果表明，所研制的焊接小车具有较好的通过性，满足使用要求。

4 结论

（1）进行了基于摩擦驱动的焊接小车受力分析和仿真验证，获得了焊接小车保持匀速运动时的牵引力变化规律。

（2）进行了焊接小车的通过性分析，获得了焊接小车的通过性公式，为焊接小车的设计提供了理论依据。

（3）根据前述结论设计了一款焊接小车，并通过仿真验证了其在通过柔性轨道时的可靠性。