基于特征模型的永磁同步直线电机自适应控制

摘 要：

为了解决永磁同步直线电机系统的参数不确定性、建模不确定性及饱和非线性等问题，提出一种基于特征模型的自适应控制器。依据特征模型理论描述永磁同步直线电机系统，采用自适应和鲁棒控制方法设计控制器。建立永磁同步直线电机的特征模型，并给出具体建立步骤，使得控制器设计变得简单，易于工程实现。通过设计参数自适应律对系统未知特征参数进行估计，可实现对系统模型的精确补偿，同时在控制器中添加带有误差积分的鲁棒控制项，提高系统对不确定参数及未知干扰的鲁棒性。此外，由于饱和特性的存在，导致控制器产生windup问题，给系统的控制性能和稳定性造成不利影响。因此，该控制器中还带有抗饱和控制项，能够提升系统的抗饱和能力。最后，通过对比实验验证了所提控制器的有效性。

关键词：永磁同步直线电机；参数不确定性；建模不确定性；饱和非线性；特征模型；自适应控制；抗饱和

DOI：10.15938/j.emc.2024.03.013

中图分类号：TM351

文献标志码：A

文章编号：1007-449X（2024）03-0131-10

收稿日期： 2022-07-04

基金项目：国家自然科学基金（61673219）

作者简介：曹 阳（1993—），男，博士研究生，研究方向为电机系统分析与控制；

郭 健（1974—），男，博士，教授，博士生导师，研究方向为智能系统与智能控制、机器人系统、高精度电机控制等。

通信作者：郭 健

Adaptive control of permanent magnet synchronous linear motor based on characteristic model

CAO Yang， GUO Jian

（School of Automation， Nanjing University of Science and Technology， Nanjing 210094， China）

Abstract：

To address the problems of parameter uncertainty， modeling uncertainty and saturation nonlinearity in the permanent magnet synchronous linear motor system， an adaptive controller based on characteristic model was proposed. A characteristic model was used to describe the permanent magnet synchronous linear motor system， and the controller was designed using adaptive and robust control methods. The characteristic model was established based on the system dynamics and parameters， and the specific steps were presented. This simplifies the controller design and facilitates the engineering implementation. An online parameter adaptation law was employed to estimate the unknown characteristic parameters of the system and achieve accurate compensation for the system model. Furthermore， an integral-type robust control term was incorporated into the controller， which improves the robustness of the system against uncertain parameters and unknown disturbances. In addition， the saturation nonlinearity leads to the windup problem in the controller， which has adverse effects on the control performance and stability of the system. Therefore， an anti-windup control scheme was devised for the controller， which can enhance the anti-saturation ability of the system. Finally， comparative experiments with other control methods were conducted to verify effectiveness of the proposed controller.

Keywords：permanent magnet synchronous linear motor; friction nonlinearity; saturation nonlinearity; armature mass variation; characteristic model; adaptive control; anti-windup

0 引 言

相比于旋转同步电机，永磁同步直线电机（permanent magnet synchronous linear motor，PMSLM）具有更高的推力密度和更快的动态响应，特别适用于对速度和精度要求较高的场合，已被广泛应用在高精密加工、轨道交通传输等现代工业领域［1-2］。但是由于采用直接驱动方式，PMSLM控制系统对参数摄动及扰动等因素变得更加敏感［3］，这会严重影响系统的控制性能。因此，保证PMSLM系统的高精度跟踪性能与抗扰动能力十分重要，对提高机床加工精度、提升交通传输效率具有重要的意义。

针对PMSLM系统的高精度跟踪问题，国内外已有众多学者对其进行了研究。文献［4］设计了一种带模型参考自适应观测器的预测电流控制策略，经过实验验证该控制策略可以实现对速度进行在线准确辨识，进而提高电流的跟踪性能。文献［5］利用扩张状态观测器和非线性状态误差反馈对PMSLM的自抗扰控制器进行优化，提高了系统的动态响应性能和抗干扰能力。文献［6］提出一种基于周期性扰动学习的自适应滑模控制方法，采用滑模控制确保PMSLM系统对不确定性因素具有较强的鲁棒性。文献［7］在系统模型反馈线性化的基础上，将H∞鲁棒控制方法与D-K迭代法相结合，提高了系统对不确定性因素影响的抑制能力。

姚斌等［8］提出一种自适应鲁棒控制方法，所开发的控制器成功应用在多种控制系统中［9-11］。为了解决非光滑饱和非线性的影响，文献［12］构造了一种新的近似饱和模型，该模型能够以任意规定的精度平滑地逼近实际饱和。此外，通过添加积分器技术，使得控制器可以消除与表面误差和边界层误差有关的耦合项。但是该方法在控制器的设计中需要对虚拟控制量重复微分，如果系统模型阶数高，会增加设计的复杂性。文献［13］提出一种考虑LuGre摩擦的自适应鲁棒控制方法，针对陀螺框架伺服系统未知惯量和阻尼系数、LuGre摩擦参数不确定性及未知外部干扰上界，设计参数更新律对其进行估计，该控制律提高了系统的跟踪精度并通过仿真结果验证了所提方法的有效性。但该方法需要被控对象的精确数学模型，另外估计的未知参数过多，多个自适应参数需要反复调试，增加了实际应用时的难度。自适应鲁棒控制可以估计系统未知参数，但如果系统模型复杂、未知参数多、某些状态不可测时，控制器的设计将面临巨大挑战。

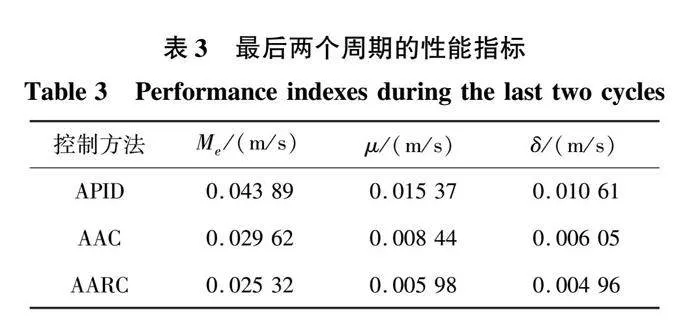
针对这些问题，吴宏鑫院士等［14-15］提出特征建模的思想，特征模型一般用一阶或二阶差分方程/微分方程来描述，有关信息都压缩到几个特征参数中，并不丢失原有的信息。特征模型建立的形式比原对象动力学方程简单，为实际复杂系统的建模问题提供了一条途径。文献［16］基于永磁同步电机的特征模型，设计一个以非线性黄金分割自适应控制为主的控制方案。通过安排过渡过程和特征模型参数的在线辨识，该控制方案实现了控制器参数的在线自适应调节。文献［17］将特征建模方法推广到具有惯性变化的齿轮传动伺服系统中，设计了一个自适应二阶离散终端滑模控制器，并实现了有限时间有界性。然而上述基于特征模型所设计的控制器没有进行抗饱和（anti-windup）研究。windup现象是指由于被控对象的输入限制，使得被控对象的实际输入与控制器的输出不等，引起系统闭环响应变差（如超调变大，调节时间变长，甚至使系统失去稳定）的现象。实际的PMSLM是个物理限制系统，转速控制器的输出必须限定在一定的范围内，使得实际电机的控制输入量不能大于一个预先设定值。当控制器输出受到饱和限制时，特别是含有积分项的控制信号仍然增加时，就会出现windup现象，使实际闭环系统的性能下降，因此对PMSLM系统设计抗饱和控制是有必要的［18-19］。

基于上述分析，针对PMSLM系统存在的参数不确定性、建模不确定性及饱和非线性等问题，提出一种基于特征模型的抗饱和自适应鲁棒控制器（anti-windup adaptive robust control based on characteristic model，AARC）。利用特征模型简化PMSLM系统的描述，并对其进行验证。然后，设计一种基于参数投影的自适应律，实现对系统模型的在线补偿。同时，将系统的不确定参数和未知干扰视为集总的干扰项，引入误差积分的鲁棒控制项进行抑制。此外，为了解决积分环节可能引起的windup现象，加入抗饱和控制项，提高系统的抗饱和能力。最后，基于Lyapunov函数证明闭环系统的稳定性，并通过实验验证所提控制器的有效性和鲁棒性。

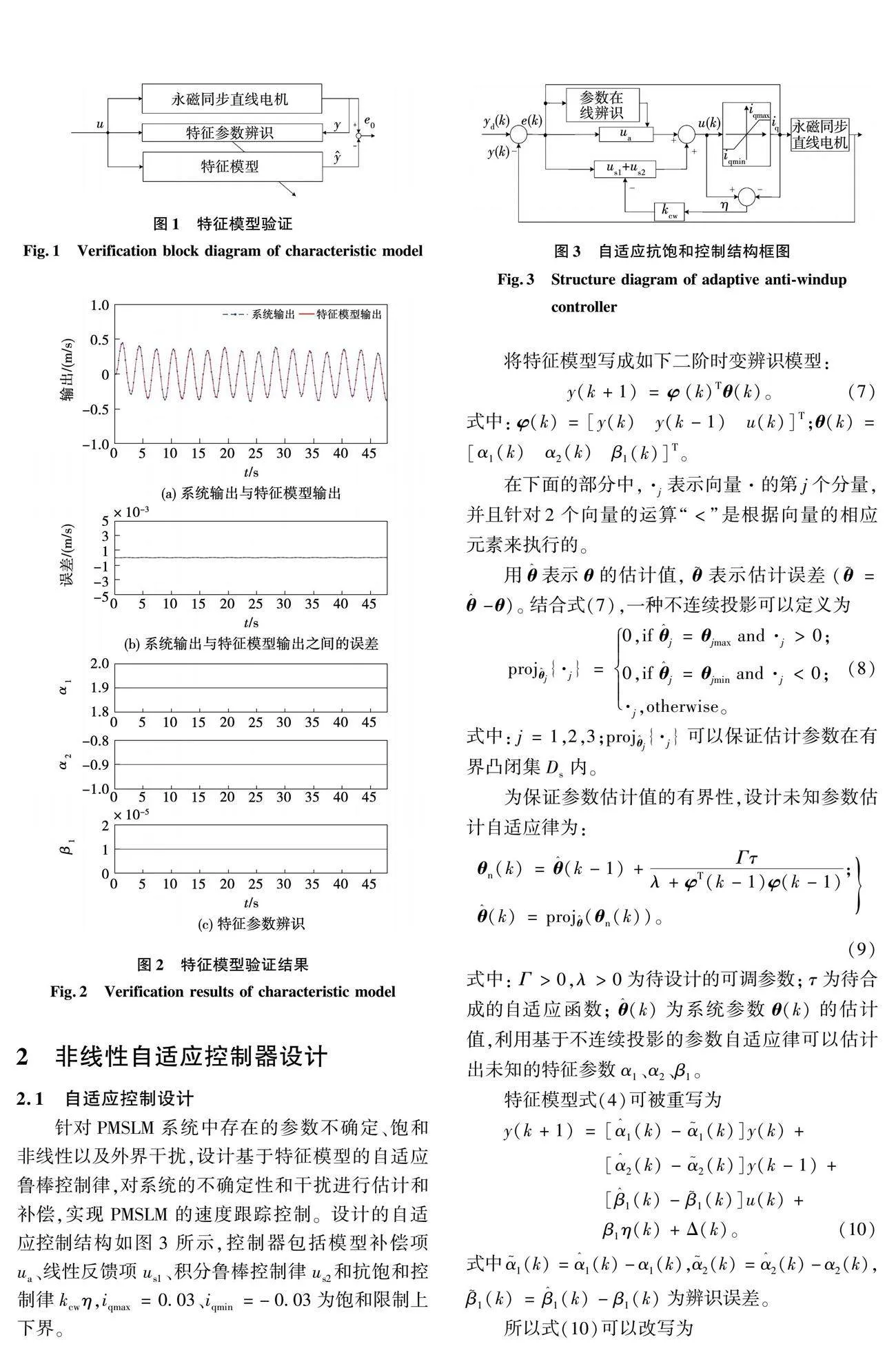
1 PMSLM的特征建模与验证

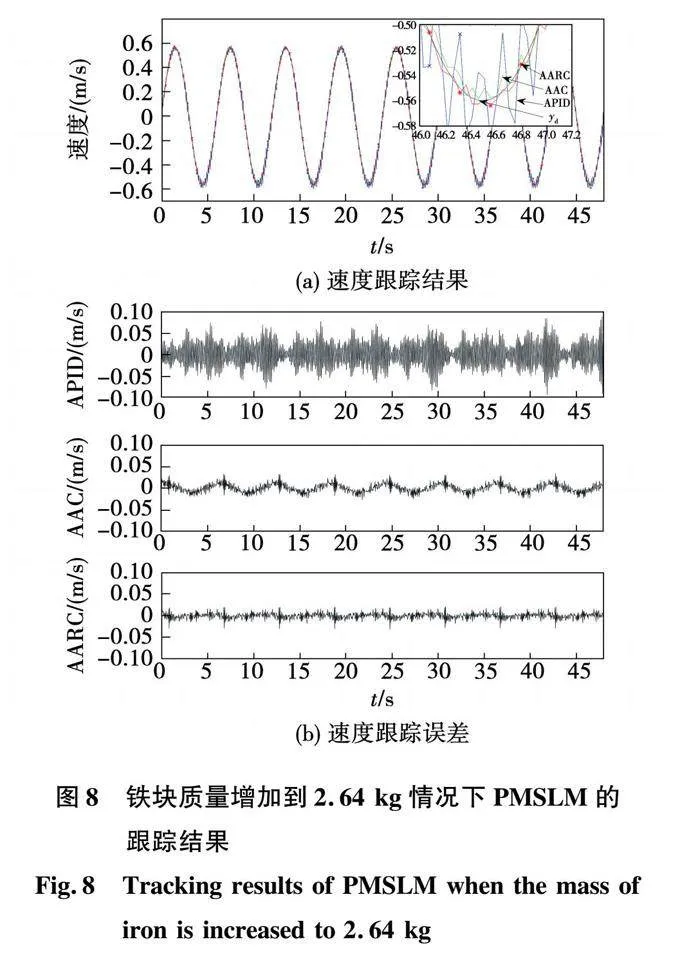
首先将给定速度设置为yd=0.56sin（3.14t） m/s。系统跟踪结果如图6所示，性能指标如表2所示。从这些实验结果可以看出，所提出的AARC控制器在瞬态和最终跟踪误差方面优于其他两种控制器，因为AARC采用了基于参数自适应的补偿和鲁棒控制项，可以同时处理参数和未建模不确定性。虽然AAC中也包含参数自适应，但对于建模的不确定性和未知扰动的抑制效果不佳。通过表2可以看出，AARC添加鲁棒项后各种误差指标会比AAC小，验证了鲁棒控制项us2的有效性。在3种控制器中，线性抗饱和PID的误差指标最差，达到了AARC的2倍以上，这说明基于非线性模型的控制器设计方法具有更大的优势。

为了进一步验证控制器对参数变化的自适应能力，设定了不同的动子质量来进行实验。给PMSLM的动子上添加1.33 kg的铁块。系统跟踪结果如图7所示，表3列出了最后两个周期的性能指标。从图7可以看出，使用AARC控制方法的控制系统，在面对动子质量变化时，其反应速度快，并且波动较小。从表3可知，APID的最大跟踪误差没有增大，意味着APID中存在大的积分增益对该扰动也有一定的抑制效果。但与上一个实验情况相比，APID的μ和δ指标增大明显，仍然比其他2个控制器差。适当的参数自适应在一定程度上也可以削弱动子质量变化给系统带来的参数不确定性影响，就像AAC那样。AARC的各项误差指标是3个控制器中最好的，再次证明了该控制器的有效性。

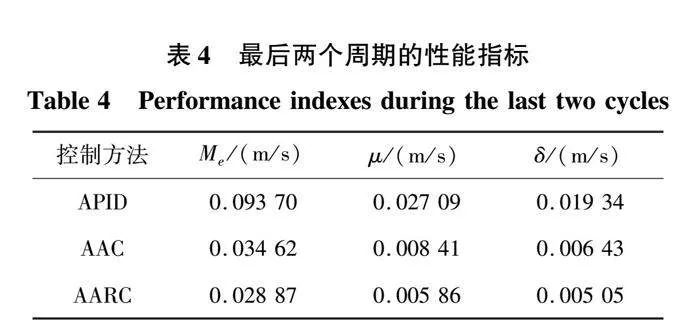
最后将动子上的铁块增加到2.64 kg，此时PMSLM受到的摩擦非线性和扰动进一步增大，3个控制器的跟踪性能都有所变差。实验结果如图8所示，误差指标见表4。在这个测试用例中，APID中的跟踪误差抖动变大，而AARC的跟踪误差则相当平滑。APID控制器表现出最差的跟踪性能，最大跟踪误差为0.094，表明APID在该跟踪任务中已经达到了其局限性。另外，即使在增大动子质量情况下，所提出的AARC控制器仍然可以对模型进行补偿并衰减未建模的扰动，从而在所有比较的控制器中达到最好的跟踪性能。

4 结 论

本文针对PMSLM系统提出一种基于特征模型的自适应控制方法，该方法能够有效地解决PMSLM系统的参数不确定性、建模误差和外部干扰等问题。首先利用二阶变差分方程对PMSLM系统进行简化建模，然后设计了一种基于特征模型的自适应控制器，仅利用系统的输入和输出信号，实现了对PMSLM系统的精确速度跟踪控制。为了提高系统的鲁棒性和抗饱和能力，还引入了鲁棒补偿项和抗饱和控制项，并严格证明了闭环系统的稳定性。最后，通过实验结果验证了所提控制方法的有效性。

本文控制器的参数是固定的，需要通过反复调试来确认。当实验条件和环境发生改变时，可能导致参数不一定是最优的。因此，在未来工作中将考虑进一步研究控制器参数的自动调整技术［21］，采用自学习的方法来替代控制器中参数的人工调整部分。

参 考 文 献：

［1］ 龚夕霞， 李焱鑫， 卢琴芬. 模块化永磁直线同步电机考虑制造公差的推力鲁棒性优化［J］. 电工技术学报， 2024， 39（2）： 465.

GONG Xixia， LI Yanxin， LU Qinfen. Thrust robustness optimization of modular permanent magnet linear synchronous motor accounting for manufacture tolerance［J］. Transactions of China Electrotechnical Society， 2024， 39（2）： 465.

［2］ 张春雷， 张辉， 叶佩青. 高霍尔位置检测精度的圆筒型永磁同步直线电机设计［J］. 电工技术学报， 2022， 37（10）： 2481.

ZHANG Chunlei， ZHANG Hui， YE Peiqing. Design of tubular permanent magnet synchronous linear motor by reliability-based robust design optimization［J］. Transactions of China Electrotechnical Society， 2022， 37（10）： 2481.

［3］ 缪仲翠， 苏乙， 张磊， 等. 梯形Halbach交替极无铁心永磁同步直线电机特性分析与优化设计［J］. 电机与控制学报， 2024， 28（1）： 164.

MIAO Zhongcui， SU Yi， ZHANG Lei， et al. Characteristic analysis and optimization design of air-core permanent magnet linear synchronous motor with trapezoidal Halbach array consequent-pole［J］. Electric Machines and Control， 2024， 28（1）： 164.

［4］ 李争， 安金峰， 肖宇， 等. 基于自适应观测器的永磁同步直线电机模型预测控制系统设计［J］. 电工技术学报， 2021， 36（6）： 1190.

LI Zheng， AN Jinfeng， XIAO Yu， et al. Design of model predictive control system for permanent magnet synchronous linear motor based on adaptive observer［J］. Transactions of China Electrotechnical Society， 2021， 36（6）： 1190.

［5］ 李争， 张梓豪， 王康涛， 等. 基于无模型的PMLSM改进自适应滑模自抗扰控制［J］. 电机与控制学报， 2024， 28（1）： 142.

LI Zheng， ZHANG Zihao， WANG Kangtao， et al. Improved adaptive sliding mode active disturbance rejection control for PMLSM based on model-free theory［J］. Electric Machines and Control， 2024， 28（1）： 142.

［6］ 张康， 王丽梅. 基于周期性扰动学习的永磁直线电机自适应滑模位置控制［J］. 电机与控制学报， 2021， 25（8）： 132.

ZHANG Kang， WANG Limei. Adaptive sliding mode position control for permanent magnet linear motor based on periodic disturbance learning［J］. Electric Machines and Control， 2021， 25（8）： 132.

［7］ 孙宜标， 毛爽， 夏加宽. 直线电机悬浮平台的μ－H∞鲁棒控制［J］. 沈阳工业大学学报， 2014， 36（1）： 7.

SUN Yibiao， MAO Shuang， XIA Jiakuan. μ－H∞robust control for linear motor levitation platform［J］. Journal of Shenyang University of Technology， 2014， 36（1）： 7.

［8］ YAO B， BU F， REEDY J， et al. Adaptive robust control of singlerod hydraulic actuators：theory and experiments［J］. IEEE/ASME Transactions on Mechatronics， 2000， 5（1）： 79.

［9］ CHEN S， CHEN Z， YAO B， et al. Adaptive robust cascade force control of 1-DOF hydraulic exoskeleton for human performance augmentation［J］. IEEE/ASME Transactions on Mechatronics， 2017， 22（2）：589.

［10］ HELIAN B， CHEN Z， YAO B. Adaptive robust motion control of a pump direct drive electro-hydraulic system with meter-out pressure regulation［J］. IFAC-Papers OnLine， 2020， 53（2）： 9005.

［11］ HAN J， YANG S， XIA L， et al. Deterministic adaptive robust control with a novel optimal gain design approach for a fuzzy 2dof lower limb exoskeleton robot system［J］. IEEE Transactions on Fuzzy Systems， 2020， 29（8）： 2373.

［12］ LIU Y. Saturated robust adaptive control for uncertain nonlinear systems using a new approximate model［J］. IET Control Theory and Applications， 2017， 11（6）： 870.

［13］ 王璐， 郭毓， 钟晨星， 等. 控制力矩陀螺框架伺服系统期望补偿自适应鲁棒控制［J］. 控制理论与应用， 2017， 34（9）： 1143.

WANG Lu， GUO Yu， ZHONG Chenxing， et al. Desired compensation adaptive robust control for control moment gyroscopes gimbal servo system［J］. Control Theory and Applications， 2017， 34（9）： 1143.

［14］ CHANG Y， JIANG T， PU Z. Adaptive control of hypersonic vehicles based on characteristic models with fuzzy neural network estimators［J］. Aerospace Science and Technology， 2017， 68： 475.

［15］ 常亚菲. 一类不确定非线性系统基于特征模型的复合自适应控制［J］. 控制理论与应用， 2019， 36（7）： 1137.

CHANG Yafei. Characteristic model-based composite adaptive control for a class of uncertain nonlinear systems［J］. Control Theory and Applications，2019， 36（7）： 1137.

［16］ 王永， 窦晓华， 方浩， 等. 永磁同步电机非线性黄金分割自适应转速控制［J］.电机与控制学报， 2017， 21（10）： 23.

WANG Yong， DOU Xiaohua， FANG Hao， et al. Nonlinear golden-section adaptive speed control of permanent magnet synchronous motor［J］. Electric Machines and Control， 2017， 21（10）： 23.

［17］ WANG X， WU Y， ZHANG E， et al. Adaptive terminal sliding-mode controller based on characteristic model for gear transmission servo systems［J］. Transactions of the Institute of Measurement and Control， 2019， 41（1）： 219.

［18］ QI L， BAO S， SHI H. Permanent-magnet synchronous motor velocity control based on second-order integral sliding mode control algorithm［J］. Transactions of the Institute of Measurement and Control， 2015， 37（7）： 875.

［19］ 张兴华， 姚丹. 感应电机直接转矩控制系统的“抗饱和”控制器设计［J］. 电工技术学报， 2014， 29（5）： 181.

ZHANG Xinghua， YAO Dan. Anti-windup speed controller design for direct torque controlled induction motor drives［J］.Transactions of China Electrotechnical Society， 2014， 29（5）： 181.

［20］ IGHACHANE M A， AKKOUCHI M. Further refinements of Young's type inequality for positive linear maps［J］. Revista de la Real Academia de Ciencias Exactas， Físicas y Naturales. Serie A. Matemáticas， 2021， 115（2）： 10.

［21］ BENOSMAN M. Learning-based adaptive control for nonlinear systems［C］//European Control Conference （ECC）， June 24-27， 2014， Strasbourg， France. 2014： 920-925.

（编辑：邱赫男）