基于谐响应的大型异步电机电磁振动分析

摘 要：

大型异步电机的电磁振动是电机振动的主要构成部分，对电机振动等级的评估需要进行准确的电磁振动分析，本文以一台10 kV兆瓦级大型异步电机为对象进行电磁振动分析。首先对完整的电机模型进行模态分析，求解固有频率及对应振型，并实验测量了电机实际运行时的固有频率；然后将电磁场二维有限元计算得到的径向电磁力作为载荷，对该电机进行谐响应分析，最后与实验测得的振动速率对比。结果表明，基于电机整机模型的模态分析和谐响应分析可以较为准确地分析大型异步电机电磁振动，能够为电机的优化设计或电磁振动抑制提供理论依据。

关键词：异步电机；电磁振动；模态分析；谐响应；电磁力；有限元

DOI：10.15938/j.emc.2024.03.012

中图分类号：TM301.4

文献标志码：A

文章编号：1007-449X（2024）03-0123-08

收稿日期： 2023-03-17

基金项目：国家自然科学基金（51777139）

作者简介：李 巍（1982—），女，博士，副教授，研究方向为电机系统及其控制、电磁场数值计算；

刘 阳（1999—），男，硕士研究生，研究方向为异步电机振动与噪声分析；

陈 伟（1983—），男，博士，研究方向为交流电机控制技术与运动控制技术。

通信作者：李 巍

Electromagnetic vibration of asynchronous electrical machine based on harmonic response

LI Wei1， LIU Yang1， CHEN Wei2

（1.College of Electronic and Information Engineering， Tongji University， Shanghai 201804， China；2.Shanghai STEP Electric Corporation， Shanghai 201801， China）

Abstract：

The electromagnetic vibration of large induction motor is the main component of the motor vibration. The evaluation of the motor vibration grade requires accurate electromagnetic vibration analysis. The electromagnetic vibration of a 10 kV megawatt induction motor was analyzed. Firstly， the mode analysis of the complete motor model was carried out to solve its natural frequency and corresponding mode， and the actual operation of the motor natural frequency was measured experimentally. Then， the radial electromagnetic force obtained by two-dimensional finite element calculation of electromagnetic field was used as the load to analyze the harmonic response of the motor. Finally， the vibration velocity was compared with that measured by experiment. The results show that the electromagnetic vibration analysis results can be obtained accurately based on the mode analysis and harmonious response analysis of the whole model of large induction motor， which can provide a theoretical basis for the optimization design of the motor or electromagnetic vibration suppression.

Keywords：induction motor; electromagnetic vibration; mode analysis; harmonic response; electromagnetic force; finite element method

0 引 言

大型异步电机的振动问题非常突出，各种应用场合对振动指标要求越来越高，如何对电机振动进行准确分析成为当下研究重点。电机振动根据成因可以分为三类：机械振动、气体振动和电磁振动［1］。机械振动主要由转子不平衡、轴承缝隙、连接松动等因素引起；气体振动是由转子转动、风扇转动等引起的空气流动、撞击、摩擦产生；电磁振动主要由定子和转子间电磁力相互作用引起电机结构发生形变而产生。近些年，由于工艺的改进和加工精度的提高，机械振动已被极大地削弱；气体振动在高速电机振动中占比较大，在低速电机中并不明显；相对而言，电磁振动是大中型电机振动的主要组成部分［2-3］。

在电机磁场中，电机各部分会因电磁力的作用发生不同程度的形变，并且形变量随时间变化，从而导致宏观上的电磁振动。已有研究表明作用于电机定子的径向电磁力是引起电磁振动的主要原因［4］。如果根据电机的设计参数能准确计算出径向电磁力，进而得到电磁力导致的振动，就可以逆向分析导致电磁振动的具体因素，并以此为依据进行电机优化设计，进而减小振动噪声。

电磁力的计算方法可大致分为两类：解析法和数值法。解析法主要包括等效磁路法、子域分析法等［5-7］。数值法中有限元法应用最为广泛［8-10］，具有较高的计算精度。得到电磁力后，可以采用动力学分析电磁力作用下的电机振动响应，常用的动力学分析方法有：模态分析、瞬态动力学分析、谐响应分析等［11］。当电磁力的频率与电机的固有频率接近且空间阶次与电机的振型相同时就会发生共振。通过模态分析能够得到电机的固有频率及振型［12］，在电机设计和控制中可以抑制对应频率的电磁力，从而避免发生共振。通过谐响应分析可以得到电机在实际工况下的振动位移，进而用于检验振动指标是否满足要求，为电机的高性能运行提供可靠的依据。

近些年来，许多学者进行了电机电磁振动的研究。文献［13］采用二维有限元法计算电磁力，并将其加载于三维模型定子齿端进行谐响应分析，通过锤击法模态实验验证了所采用分析方法的可行性。文献［14］对电机的二维模型、三维模型及加强筋、底角等结构进行了模态分析，对比分析了各结构对电机固有频率的影响。文献［15］建立包含电机机壳的三维有限元模型，将电磁力施加在定子齿部表面进行瞬态动力学计算，并通过加速度测量实验进行了验证。文献［16］采用解析法和模态分析计算了一台50 kW永磁同步电机定子的固有频率，采用磁-固耦合法进行振动分析并进行了实验验证。通过以上研究可以看出，模态分析是得到电机的固有频率及对应振型的有效方法之一，二维电磁计算和三维谐响应分析可以相对准确计算出电机的振动响应。大型电机结构复杂、连接约束多，在采用上述方法进行振动分析时需要考虑不同因素的影响。

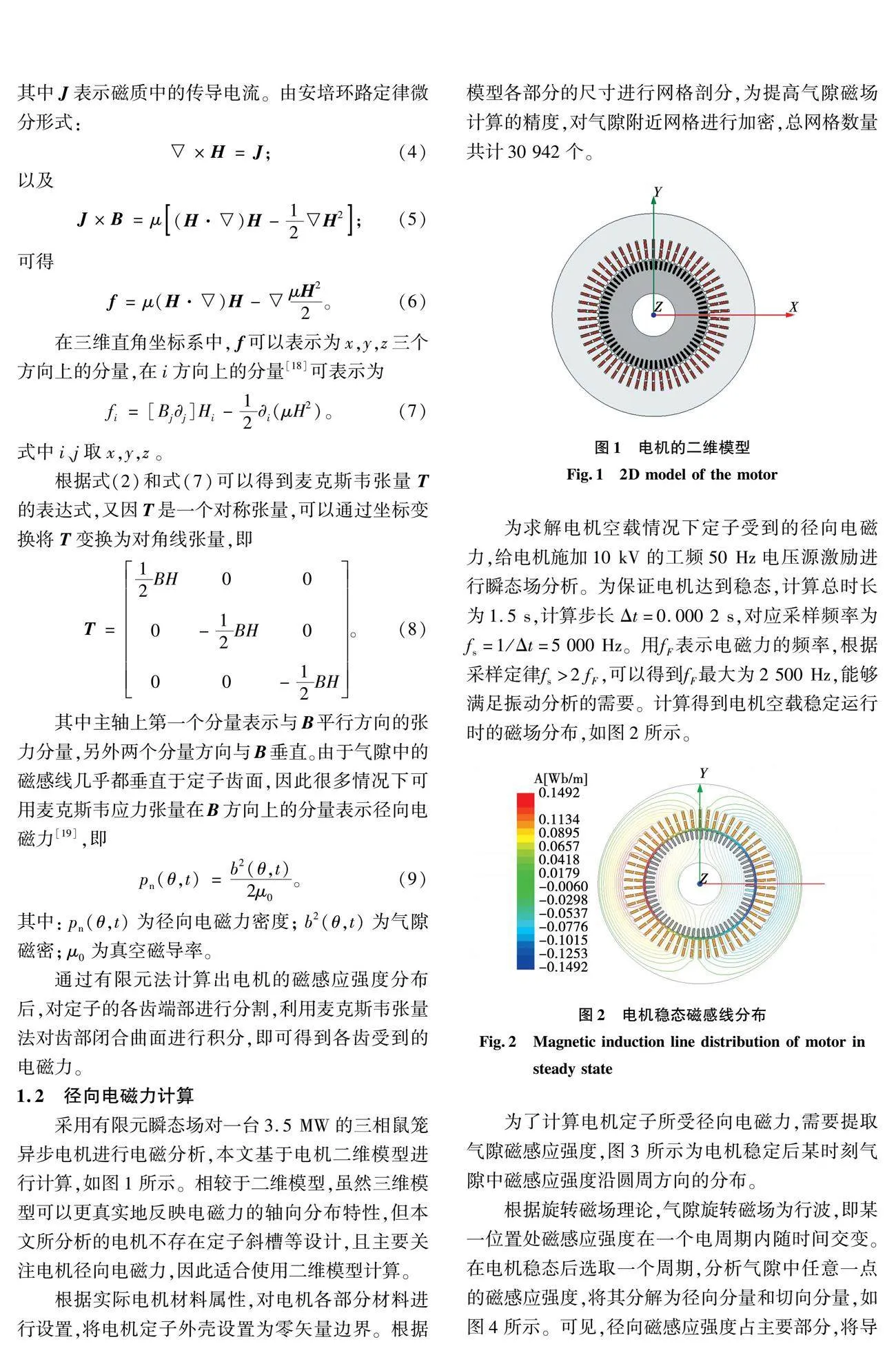
本文对一台兆瓦级异步电机进行电磁振动分析。首先根据电机参数建立完整的电机三维模型，包含定子、转子、机壳等部分。通过模态分析求解出该电机的固有频率及振型。建立电机定转子的二维模型，采用有限元法进行电磁计算，通过麦克斯韦张量法求出电机定子受到的径向电磁力。将计算的径向电磁力加载至电机三维模型的定子齿部，通过谐响应分析得到电机振动速率的频域响应。为了验证所采用计算分析方法的有效性，对电机进行振动实验研究。采用振动传感器测量电机不同运行状态时的振动速率，得到电机的固有频率。将实验结果与模态分析结果及谐响应分析结果进行对比，通过模态分析和谐响应分析能够较为准确计算出电机固有频率和振动速率的频谱。

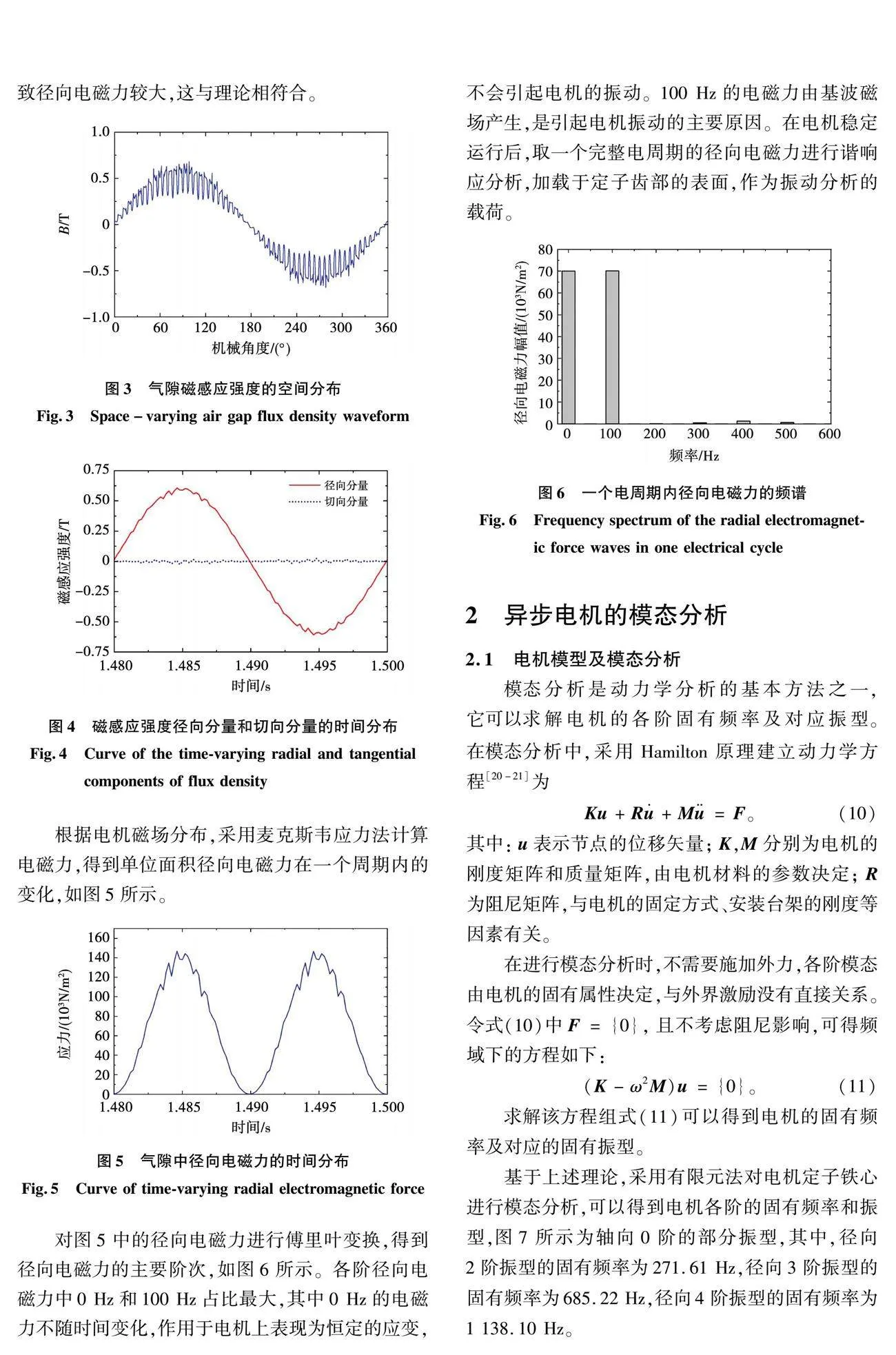
为求解电机空载情况下定子受到的径向电磁力，给电机施加10 kV的工频50 Hz电压源激励进行瞬态场分析。为保证电机达到稳态，计算总时长为1.5 s，计算步长Δt=0.000 2 s，对应采样频率为fs=1/Δt=5 000 Hz。用fF表示电磁力的频率，根据采样定律fsgt;2fF，可以得到fF最大为2 500 Hz，能够满足振动分析的需要。计算得到电机空载稳定运行时的磁场分布，如图2所示。

为了计算电机定子所受径向电磁力，需要提取气隙磁感应强度，图3所示为电机稳定后某时刻气隙中磁感应强度沿圆周方向的分布。

根据旋转磁场理论，气隙旋转磁场为行波，即某一位置处磁感应强度在一个电周期内随时间交变。在电机稳态后选取一个周期，分析气隙中任意一点的磁感应强度，将其分解为径向分量和切向分量，如图4所示。可见，径向磁感应强度占主要部分，将导致径向电磁力较大，这与理论相符合。

根据电机磁场分布，采用麦克斯韦应力法计算电磁力，得到单位面积径向电磁力在一个周期内的变化，如图5所示。

对图5中的径向电磁力进行傅里叶变换，得到径向电磁力的主要阶次，如图6所示。各阶径向电磁力中0 Hz和100 Hz占比最大，其中0 Hz的电磁力不随时间变化，作用于电机上表现为恒定的应变，不会引起电机的振动。100 Hz的电磁力由基波磁场产生，是引起电机振动的主要原因。在电机稳定运行后，取一个完整电周期的径向电磁力进行谐响应分析，加载于定子齿部的表面，作为振动分析的载荷。

2 异步电机的模态分析

2.1 电机模型及模态分析

模态分析是动力学分析的基本方法之一，它可以求解电机的各阶固有频率及对应振型。在模态分析中，采用Hamilton原理建立动力学方程［20-21］为

Ku+Ru·+Mu··=F。（10）

其中：u表示节点的位移矢量；K，M分别为电机的刚度矩阵和质量矩阵，由电机材料的参数决定；R为阻尼矩阵，与电机的固定方式、安装台架的刚度等因素有关。

在进行模态分析时，不需要施加外力，各阶模态由电机的固有属性决定，与外界激励没有直接关系。令式（10）中F={0}，且不考虑阻尼影响，可得频域下的方程如下：

（K－ω2M）u={0}。（11）

求解该方程组式（11）可以得到电机的固有频率及对应的固有振型。

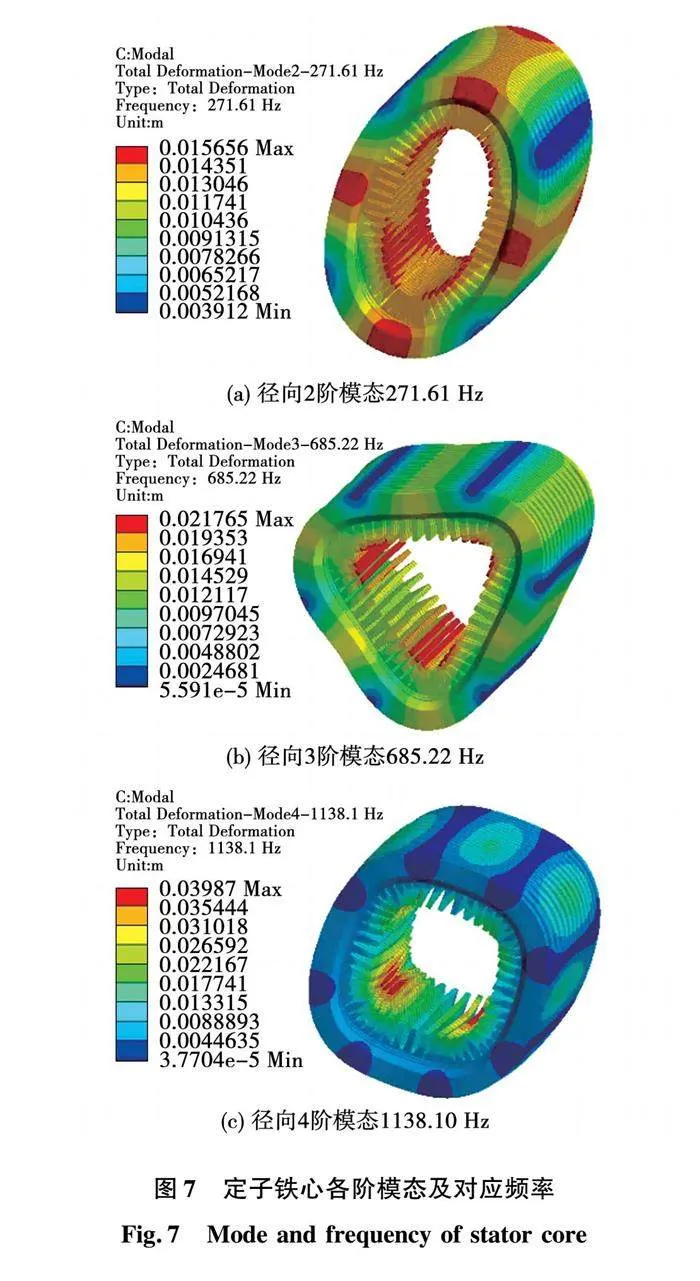
基于上述理论，采用有限元法对电机定子铁心进行模态分析，可以得到电机各阶的固有频率和振型，图7所示为轴向0阶的部分振型，其中，径向2阶振型的固有频率为271.61 Hz，径向3阶振型的固有频率为685.22 Hz，径向4阶振型的固有频率为1 138.10 Hz。

从图7可以看出，若仅对定子铁心进行模态分析，计算的定子铁心固有频率高于电机正常工作时主要激励源的频率，无法反映出整个电机的低阶模态。因此有必要对电机整体进行模态分析［22］。

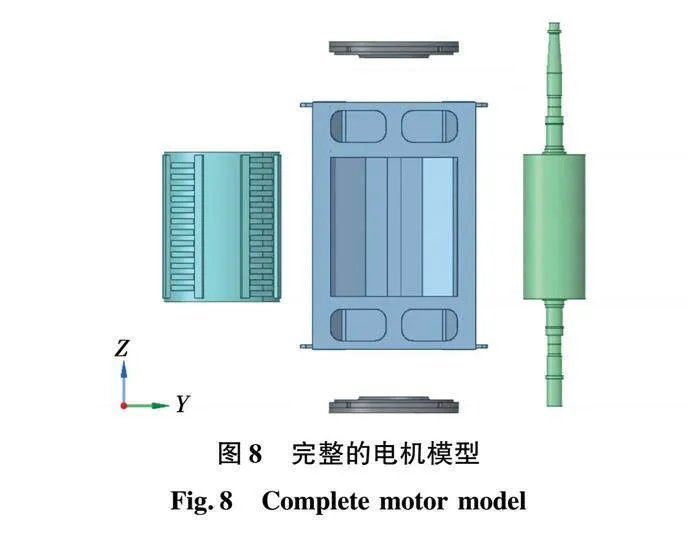
完整的电机模型包括定子铁心、端盖、转子以及加强筋等结构。图8所示为完整的电机模型主要组成部分的俯视图。图8直角坐标系中，Z方向为电机的轴向，Y方向电机水平方向，X方向与YZ平面垂直。

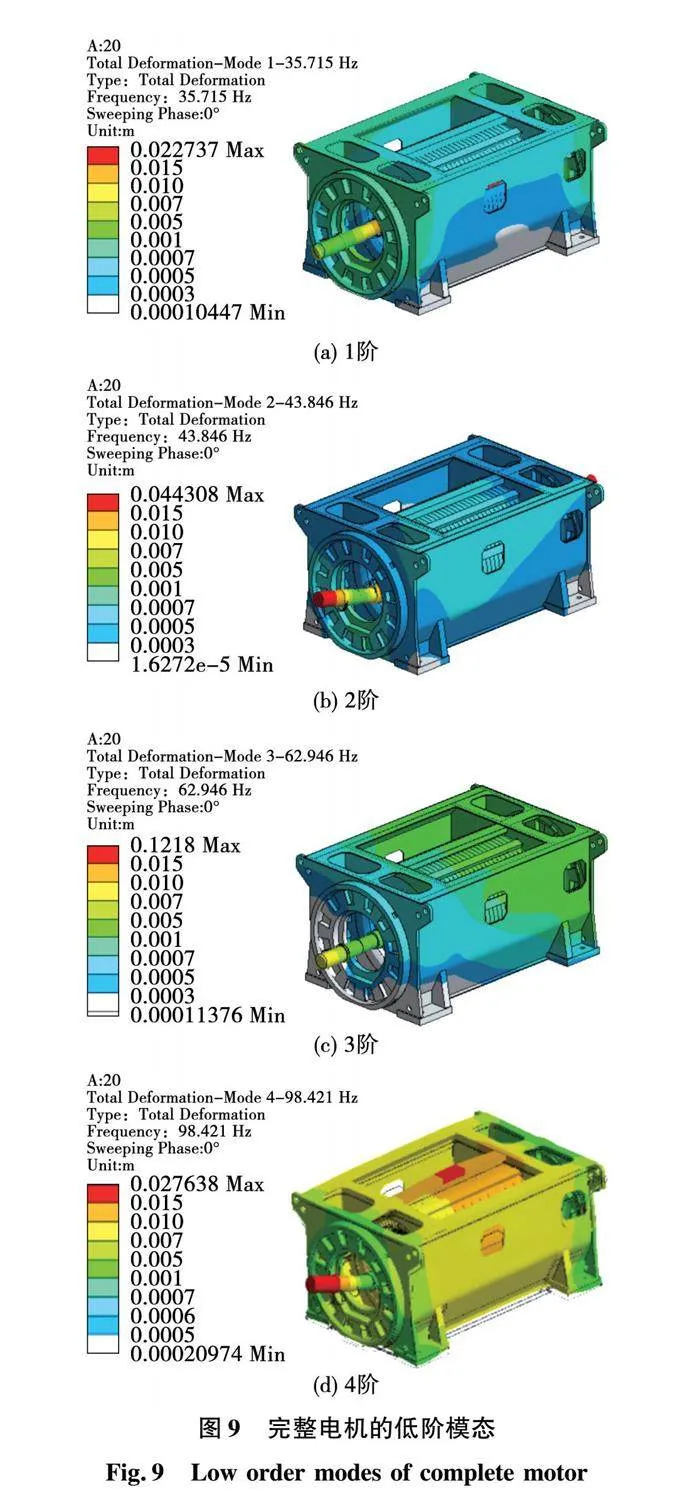
在电机底座的螺栓孔处添加Bushing约束及弹簧单元，模拟电机在地面的固定状态。不考虑定子硅钢片、支撑结构间的相对滑动，在阻尼比为零的条件下进行模态分析。图9展示了前四阶固有频率对应的电机振型。

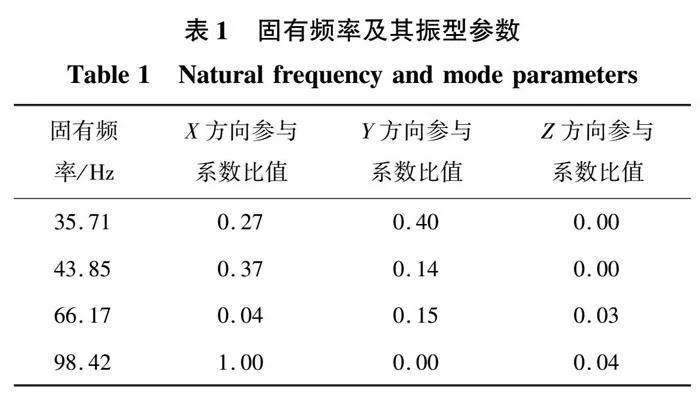
与单独定子铁心模型相比，完整电机模型的振型更为复杂。在任一固有频率下，电机在xyz三个方向的振动位移和运动质量各不相同，可以据此总结出振型的特点。本文中使用参与系数γ描述电机在每个方向振动的程度，其定义为

2.2 电机模态实验结果与仿真结果对比

对于中小型电机，许多研究［4，13］通过锤击法进行模态测试并取得了很好的效果，但对于大型电机而言很难通过锤击法激发出振动模态，而且复杂的机壳结构会导致激振点的选取很困难。本文根据电机实际应用的工况，通过电机升速和超速实验直接测量电机在多个转速下的振动响应，从而得到固有频率。

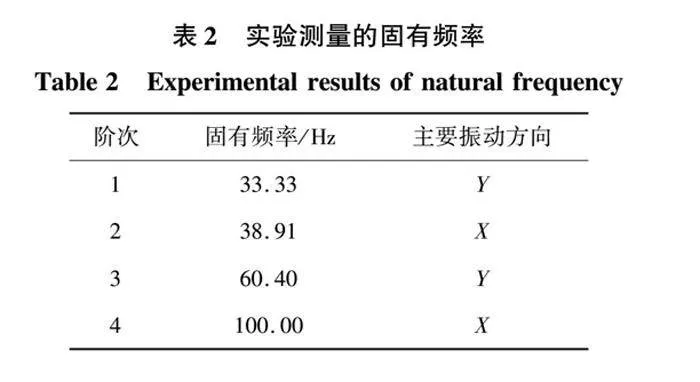
实验中，使电机在恒定磁通下从0加速至额定转速3 000 r/min，完成升速实验。然后在恒定电压10 kV下电机从3 000 r/min加速至3 600 r/min，完成超速实验。通过在电机端盖安装的速度型振动传感器测量X、Y两个方向的振动速率。实验所用电机的转子动平衡度为G0.7，因此可以忽略转子动平衡对实验结果的影响。根据升速、超速实验的测量数据可以得到各转速下电机的振动频谱，从而分析出电机的固有频率。实验得到的固有频率结果如表2所示。

从实验结果中可以看出，第一阶、第三阶固有频率在Y方向的振动幅度大于其他方向；第二阶、第四阶固有频率在X方向的振动幅度大于其他方向。

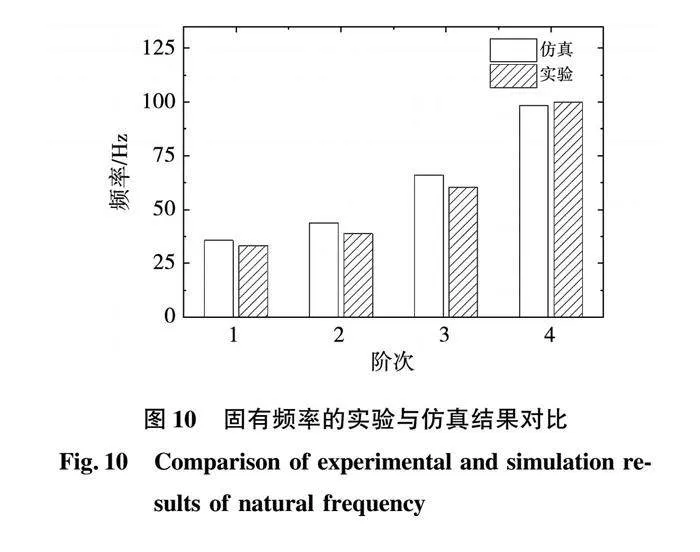
将表1中的仿真结果与表2中的实验结果进行对比，如图10所示，固有频率比较接近，对应的振型方向也一致，仿真结果与实验结果具有较高的一致性。结果表明，对完整电机的模态分析能够较为准确地计算出电机的固有频率，电机每个结构都会对各阶模态的频率及振型产生一定的影响，因此建立完整的电机仿真模型可以得到更接近实际情况的分析结果。

3 异步电机的谐响应分析

3.1 谐响应分析

当电机稳定工作时，电机定子受到的径向电磁力可分解为一系列不同频率的正弦分量，是周期性简谐载荷，可以作为谐响应分析的激励。同时，正常工作中电机的形变很小，可忽略非线性特征。因此可以通过谐响应分析研究径向电磁力作用下电机的振动响应。

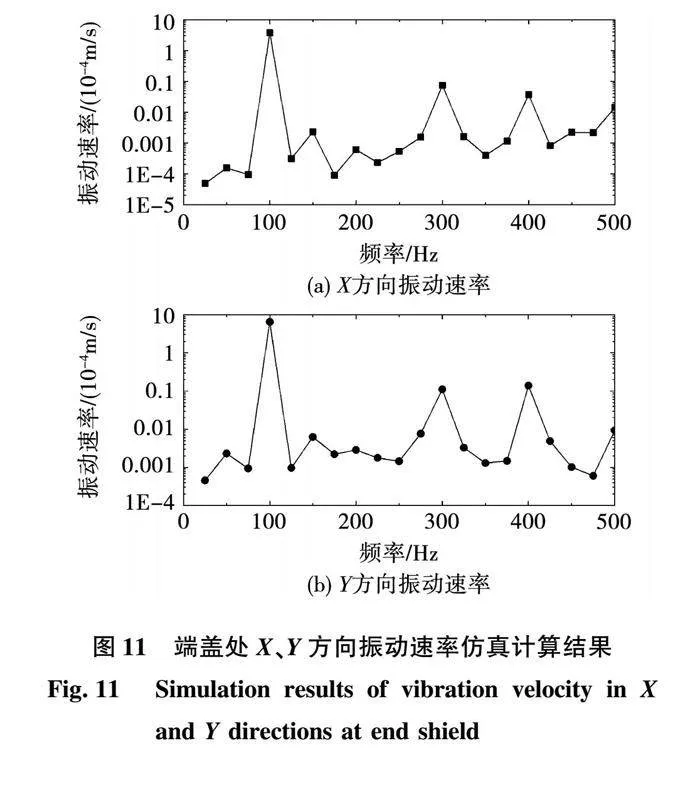
将磁场分析中计算得到的电磁力加载于电机三维模型的定子齿端，计算0至500 Hz范围内电机端盖处的频率响应，结果如图11所示。图11中纵轴为振动速率，采用对数刻度，单位为m/s；横轴为振动频率，单位为Hz。在X、Y方向的振动速率的频谱中，100 Hz对应的分量占比最大，其他分量可以忽略，这与径向电磁力的分布相对应。

3.2 谐响应实验结果与仿真结果对比

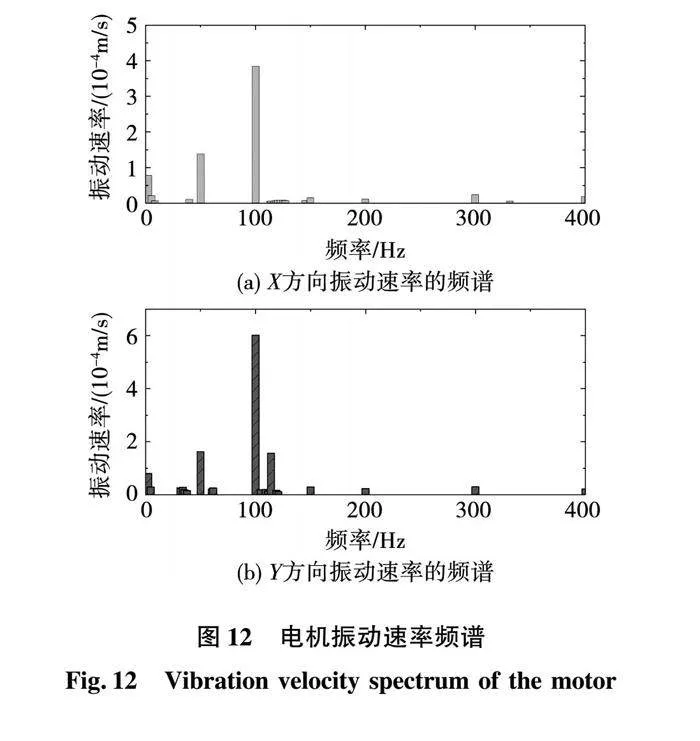
在10 kV额定电压激励下，测量电机空载状态时的振动响应。在电机端盖安装振动传感器进行测量，电机到达稳态后，连续10分钟记录X、Y方向的振动速率并计算其频谱。图12为10 kV电压下X、Y方向振动速率的频谱。

从图12中可以看出，测量结果中50 Hz和100 Hz对应的振动分量占比较大，50 Hz的振动主要由转子旋转的机械振动引起的，100 Hz的振动主要由径向电磁力引起的。对比100 Hz下实验和仿真的振动速率，如表3所示，可以看出X、Y方向上振动速率的仿真结果与实验结果都比较一致，证明了所采用的振动分析方法的有效性。

4 结 论

本文对大型异步电机的电磁振动问题进行了研究。采用模态分析对完整的电机模型进行了固有频率计算，将二维有限元计算的电磁力耦合到电机的定子齿部进行了谐响应分析，得到了电机的振动响应，并与实验测试结果进行了对比。基于上述研究得到以下结论：

1）通过对比大型异步电机的定子三维模型和整机模型的模态分析结果，发现定子模型的固有频率较高；整机模型的固有频率更丰富，包含许多低阶固有频率，且电机的振型主要表现为径向的平移。因此在对大型异步电机进行模态分析时需要考虑支撑结构及转子带来的影响。

2）根据谐响应分析能够较为准确地计算出电机的电磁振动响应。从电机振动的频谱可以看出，大型异步电机的电磁振动主要表现为2倍电频率的振动，这与电磁力频谱中幅值最大的2倍频分量相对应；高阶电磁力引起的振动占比很小。

3）电磁振动的仿真分析结果与实际测量值存在误差。大型异步电机的振动实验测试结果受到测量位置、电机固定强度、部件连接刚度等因素影响，而有限元仿真中，虽然可以通过设置电机材料、固定方式、阻尼等参数对实际情况进行模拟，但无法完全与实际工况保持一致。

4）仿真和实验结果证明了所采用振动分析方法的有效性。振动分析能够为电机的振动抑制提供依据，评估电机的振动指标是否合格，从而为电机设计或控制算法的优化提供参考。

参 考 文 献：

［1］ 陈永校， 诸自强， 应善成. 电机噪声的分析和控制［M］. 杭州：浙江大学出版社， 1987.

［2］ 王玎， 祝长生， 符嘉靖. 基于有限元的异步电机电磁振动分析［J］. 振动与冲击， 2012， 31（2）： 140.WANG Ding， ZHU Changsheng， FU Jiajing. Electromagnetically excited vibration analysis for an asynchronous electrical machine with finite element method［J］. Journal of Vibration and Shock， 2012， 31（2）： 140.

［3］ SHIOHATA K. Review of research in Japanon electromagnetic force induced vibration and noise from an electrical motor［J］. Journal of System Design and Dynamics， 2013， 7（2）： 127.

［4］ 代颖， 崔淑梅， 宋立伟. 车用电机的有限元模态分析［J］. 中国电机工程学报， 2011， 31（9）： 100.

DAI Ying， CUI Shumei， SONG Liwei. Finite element method modal analysis of driving motor for electric vehicle［J］. Proceedings of the CSEE， 2011， 31（9）： 100.

［5］ 董佳波. 异步电机电磁振动研究综述［J］. 防爆电机， 2022， 57（3）： 75.Dong Jiabo. Research overview on electromagnetic vibration of induction motors［J］. Explosion-proof" Electric Machine， 2022， 57（3）： 75.

［6］ 丁嘉露. 永磁同步电机振动噪声预测分析［D］. 沈阳：沈阳工业大学， 2020.

［7］ 屈仁浩， 蒋伟康. 电机定子铁芯振动特性分析的一种解析方法［J］. 振动与冲击， 2021， 40（3）： 81.QU Renhao， JIANG Weikang. An analytical method for vibration characteristics analysis of motor stator core［J］. Journal of Vibration and Shock， 2021， 40（3）： 81.

［8］ 黄厚佳， 李全峰， 徐余法. 基于有限元法的永磁同步电机定子固有频率研究［J］. 电机与控制应用， 2019， 46（4）： 65.HUANG Houjia，LI Quanfeng，XU Yufa. Research on the natural frequency of stator of permanent magnet synchronous motor based on finite element method［J］. Electric Machines and Control Application， 2019， 46（4）： 65.

［9］ 刘海龙. 大型感应电动机电磁力及振动特性分析［D］. 沈阳：沈阳工业大学， 2007.

［10］ 郑江， 代颖， 石坚. 车用永磁同步电机的电磁噪声特性［J］. 电工技术学报， 2016， 31（S1）： 53.

ZHENG Jiang，DAI Ying， SHI Jian. Electromagnetic noise characteristics of permanent magnet synchronous motor applied in electric vehicle［J］. Transactions of China Electrotechnical Society， 2016， 31（S1）： 53.

［11］ 李斌奇. 永磁同步电机振动的计算与分析［D］. 杭州：浙江大学， 2022.

［12］ 王宏华， 王治平， 江泉. 开关型磁阻电动机固有频率解析计算［J］. 中国电机工程学报， 2005， 25（12）： 133.WANG Honghua，WANG Zhiping，JIANG Quan. Analytical calculating of natural frequencies of stators of switched reluctance motor based on electromechanical analogy method［J］. Proceedings of the CSEE， 2005，25（12）： 133.

［13］ 李晓华， 黄苏融， 李良梓. 电动汽车用永磁同步电机振动噪声的计算与分析［J］. 电机与控制学报， 2013， 17（8）： 37.LI Xiaohual，HUANG Surong，LI Liangzi. Calculation and analysis of vehicle vibration and noise of permanent magnet synchronous motor applied in electric vehicle［J］. Electric Machines and Control， 2013， 17（8）： 37.

［14］ 温嘉斌， 崔斯柳. 感应电机振动特性有限元分析［J］. 防爆电机， 2011， 46（1）： 1.WEN Jiabin， CUI Siliu. Finite-element analysis on vibration features of induction motor［J］. Explosion-proof Electric Machine， 2011， 46（1）： 1.

［15］ 谢颖， 刘海松， 吕森， 等. 计及转子斜槽时笼型感应电机电磁振动变化规律的研究［J］. 中国电机工程学报， 2015， 35（15）： 3948.XIE Ying， LIU Haisong， L Sen， et al. Study on the variation laws of electromagnetic vibration considered the skewed rotor in a squirrel-cage induction motor［J］. Proceedings of the CSEE， 2015， 35（15）： 3948.

［16］ 陈少先，丁树业，申淑锋，等.船舶用表贴式永磁同步电机的电磁振动分析与抑制［J］.电工技术学报，2023，38（5）：1275.

CHEN Shaoxian， DING Shuye，" SHEN Shufeng， et al. Analysis and suppression of electromagnetic vibration of surface mounted permanent magnet synchronous motor for ships［J］. Transactions of China Electrotechnical Society， 2023， 38（5）： 1275.

［17］ 汤蕴璆. 电机内的电磁场［M］. 北京：科学出版社， 1981.

［18］ DAVIS A， ONOOCHIN V.The Maxwell stress tensor and electromagnetic momentum ［J］. Progress in Electromagnetics Research Letters， 2020， 94： 151.

［19］ 戈宝军， 周晓炎， 陶大军， 等. 双三相感应电机容错运行状态电磁力分析［J］. 哈尔滨理工大学学报， 2021， 26（2）： 75.GE Baojun， ZHOU Xiaoyan， TAO Dajun， et al. Electromagnetic force analysis of double three-phase induction motor operating in fault-tolerant state［J］. Journal of Harbin University of Science and Technology， 2021， 26（2）： 75.

［20］ 王天煜， 王凤翔. 大型异步电动机定子振动与模态分析［J］. 中国电机工程学报， 2007，27（12）： 41.WANG Tianyu， WANG Fengxiang. Vibration and modal analysis of stator of large induction motors［J］. Proceedings of the CSEE， 2007，27（12）： 41.

［21］ 王慧斌， 李德友， 段雪晴， 等. 基于谐响应分析的冲击式水轮机转轮共振预测［J］. 大电机技术， 2024（2）： 50.WANG Huibin， LI Deyou， DUAN Xueqing， et al. Resonance prediction of pelton turbine runner based on harmonic response analysis［J］.Large Electric Machine and Hydraulic Turbine， 2024（2）： 50.

［22］ CHAUVICAURT F， FARIA C， DZIECHCIARZ A， et al. Infuence of rotor geometry on NVH behavior of synchronous reluctance machine［C］// 10th International Conference on Ecological Vehicles and Renewable Energies， EVER 2015， March 31-April 2， Monte-Carlo， Monaco. 2015：1-6.

（编辑：刘素菊）