三相电力弹簧的无源控制策略研究

摘 要：

针对太阳能、风能等新能源设备大规模并入电网造成的电能质量下降问题，近年来出现了电力弹簧（ES）的概念。依据推导出的三相电力弹簧（TPES）的数学模型，搭建了对应的系统模型，依据无源控制（PBC）理论，分析了系统的无源性，并分别采用传统PI控制和无源控制验证了三相电力弹簧能够维持关键负载（CL）电压的稳定。通过仿真和实验验证，在有功功率变动工况下，无源控制的超调量远远低于PI控制的13.7%，调节时间0.03 s也低于PI控制的0.07 s，静差率0.000 2%也小于PI控制的0.08%，表明无源控制的动态性能和静态性能都更出色。此外，相比于传统的PI控制，无源控制所需参数更少，控制系统结构更加简单。

关键词：新能源；电力弹簧；三相电力弹簧；关键负载；无源控制；电能质量；电压稳定

DOI：10.15938/j.emc.2024.03.011

中图分类号：TM712

文献标志码：A

文章编号：1007-449X（2024）03-0110-13

收稿日期： 2023-03-22

基金项目：国家自然科学基金（62303301）

作者简介：赵永熹（1979—），女，博士，副教授，研究方向为柔性输电技术、储能技术；

张家领（1996—），男，硕士研究生，研究方向为电力电子控制；

程启明（1965—），男，博士，教授，研究方向为电力系统自动化、发电过程控制、先进控制及应用。

通信作者：程启明

Passivity-based control strategy of three-phase electric springs

ZHAO Yongxi， ZHANG Jialing， CHENG Qiming

（College of Automation Engineering， Shanghai University of Electric Power， Shanghai 200090， China）

Abstract：

In recent years， the concept of electric springs （ES） has been proposed to reduce the power quality caused by the large-scale integration of solar energy， wind energy and other new energy equipment into the power grid. Based on the derived mathematical model of three phase electric springs （TPES）， the corresponding system model was built. Based on the passivity-based control （PBC） theory， the passivity of the system was analyzed. The traditional PI control and passive control were used respectively to verify that the three-phase power spring can maintain the voltage stability on the critical load （CL）.Through simulation and experimental verification， under the active power variation condition， the overshoot of passive control is far lower than 13.7% of PI control， the adjustment time of 0.03 s is also lower than 0.07 s of PI control， and the static error rate of 0.000 2% is also less than 0.08% of PI control， indicating that the dynamic and static performance of passive control is better. In addition， compared with traditional PI control， passive control requires fewer parameters and has a simpler control system structure.

Keywords：new energy; electric spring; three-phase electric spring; critical load; passivity-based control; power quality; voltage stabilization

0 引 言

近年来可再生能源发电在电网中所占的比例越来越大［1］，有效地缓解了能源缺乏带来的压力［2］，但是可再生能源发电有着间歇性和忽高忽低不能保持稳定的特点，因此会造成电网电压不稳定［3-4］，进而造成用户侧的电能质量过低。这种情况下三相电力弹簧（electric springs，ES）作为一种全新方法被提出用来解决用户侧电能质量过低的问题。不同的负荷有着不同的功能，不同的功能决定了负荷要工作在不同的情况下。根据不同的情况，负荷能够被大致分为两类：第1类是对电能质量要求较高的关键负载，关键负载允许电压在极小的范围内发生波动，几乎不接受调节，比如医疗设备、涉及微电网区域安全的监控设备；另一类则正好相反，非关键负载允许电压在一个较大的范围内发生波动，它主要包含纯阻性设备、部分阻感性两种负荷，其中，纯阻性设备有电热类负荷和部分照明设备，比如电热毯和楼道中的电灯泡，都允许电压在较大的范围波动，而阻感性设备则是固体蓄热式电炉等设备，可以在电压过高时存储热能供其余时间段使用。为了改变流经非关键负载上的电流，三相电力弹簧需要通过调整自身的输出电压，比如电热毯等。为了改变流经非关键负载上的电流，三相电力弹簧需要通过调整自身的输出电压，因而能够把电网中电压以及功率的波动转移到非关键负载上，尽可能减少对储能电池容量的需求，并将关键负荷的电能质量有效地维持在一个较高的水平［5］。

从电力弹簧的概念首次被提出到现在，经过不断的改进和发展，电力弹簧已经衍生出多个不同版本。文献［6］详细介绍了电力弹簧的应用场景和一些基本原理。目前常见的电力弹簧主要有3种拓扑结构：第1代电力弹簧［7］、第2代电力弹簧［8-10］以及ES-B2B［11］。针对电力弹簧的工作性能，文献［12］和［13］通过详细地分析，推断出了电力弹簧能够稳定运行的范围；文献［14］将电力弹簧和静止同步补偿器做了对比，结果得出电力弹簧相比于静止同步补偿器能够更好地保证电能质量。文献［15］和［16］则是根据相量图中的几何关系，研究出了相位控制方法，这种方法将比例谐振控制与关键负荷的相位角相结合，保证电能质量在一个较高的水平。这种方法也同样存在缺点，例如对相关的参数依赖程度很高，因此不适用于大多数场合；在文献［17］中，采用了结构简单，易于控制，抗干扰能力较低，调节精度亦不高的PI控制来控制电力弹簧上的电压以及相位；根据文献［18］提出了一种基于遗传算法的控制策略，但是该方法并没有解决最佳功率补偿和电池容量等问题。

当今的三相电力弹簧控制策略大多适用于一些简单的线性对象，例如PI控制、相位控制。PI控制对于抑制负序电流和谐波有着极大的不足［19］。但是对于一些包含着多种变量以及有着很强非线性的系统来说，鲁棒性不强、调节精度不高等问题就会尤为突出。一个很好的例子就是当电网的电压有大幅度的波动时，控制性能就会很难得到保证。针对此种情况，作为非线性控制的无源控制就被提了出来。无源控制（passivity-based control，PBC）是由Ortega R等提出的一种非线性反馈的能量控制方法。无源性系统的能量由初始时刻到目前时刻的增长量不大于外部注入的能量总和，也即无源系统的运动问题伴随着能量的损失。无源控制利用输出反馈使得闭环系统特性表现为一无源映射，它采用欧拉-拉格朗日（Euler-Lagrange，E-L）数学模型，通过能量整形和阻尼注入，注入合适的阻尼项，配置系统能量耗散特性方程中的无功分量“无功力”，迫使系统总能量跟踪预期的能量函数，保证系统的稳定性，使得被控对象的输出渐近收敛到期望值。无源控制充分利用系统的物理结构，无需补偿不影响稳定性的“无功力”部分非线性项，简化了控制器设计。它通过选择不同的能量函数和阻尼注入方法，可设计多种高性能无源控制方法，对系统参数变化及外来摄动有较强鲁棒性，并且系统的结构简明易懂，易于实施，并保持全局的稳定性，不会出现奇异点。无源控制的原理可以概括为，从能量的角度入手，可以得出一个最符合系统的存储函数，使得该系统最终能够实现目标，同时该方法也具备结构简单、抗干扰能力强、稳定性好等优点。近年来，无源控制在不同的系统中被越来越多的应用 ［20-22］。

为了解决上面提出的问题，本文结合E-L模型和传统的电力弹簧模型，通过分析三相电力弹簧的数学模型和工作原理，建立一个基于E-L的三相电力弹簧的数学模型。随后，通过相关公式证明模型的无源性，为了实现电流解耦无源控制，采用注入阻尼的方法，并通过实验验证无源控制下的三相电力弹簧可以提高用户侧关键负载的电能质量。

1 三相电力弹簧的工作原理

1.1 三相电力弹簧的基本拓扑结构

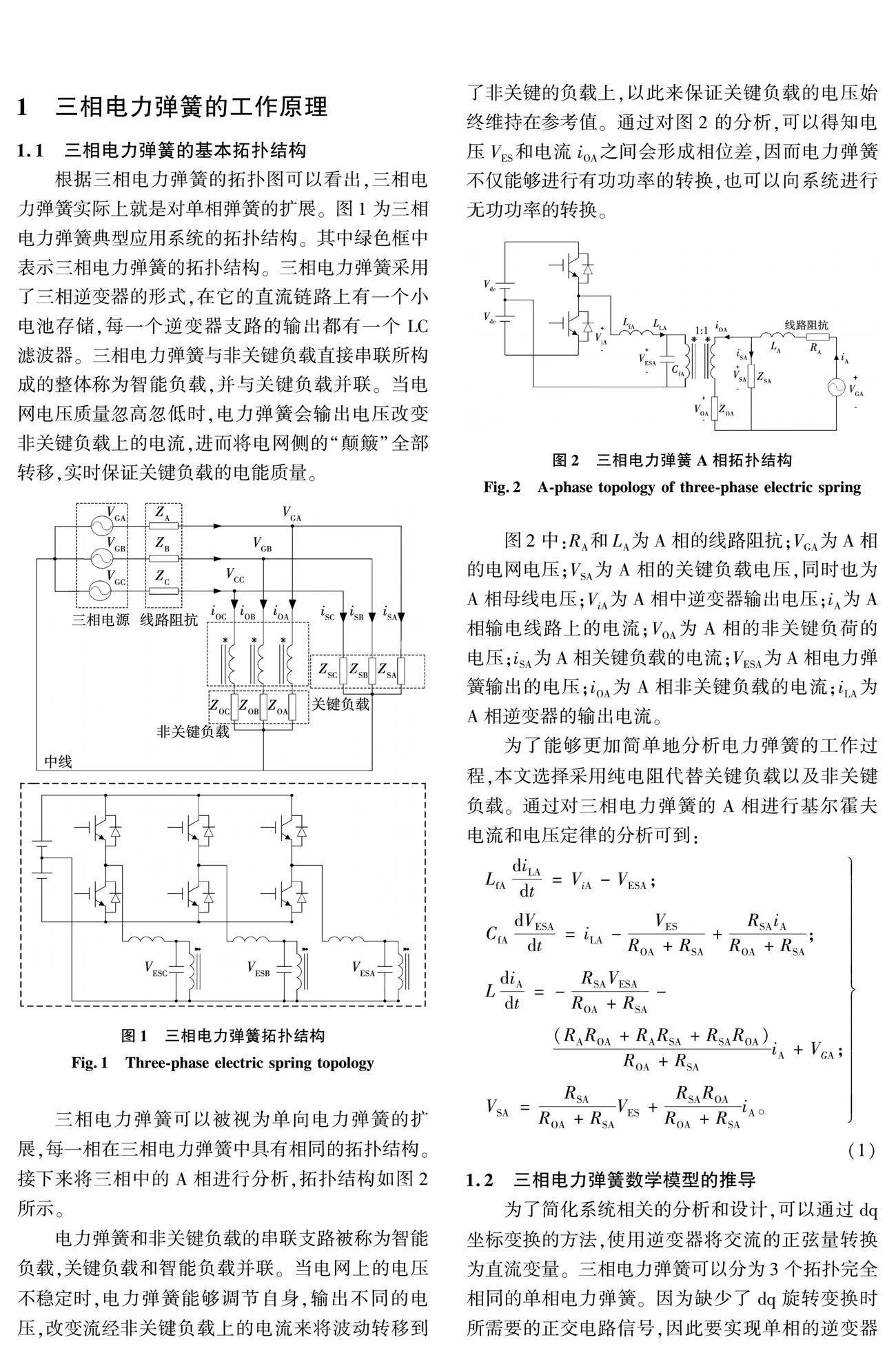
根据三相电力弹簧的拓扑图可以看出，三相电力弹簧实际上就是对单相弹簧的扩展。图1为三相电力弹簧典型应用系统的拓扑结构。其中绿色框中表示三相电力弹簧的拓扑结构。三相电力弹簧采用了三相逆变器的形式，在它的直流链路上有一个小电池存储，每一个逆变器支路的输出都有一个LC滤波器。三相电力弹簧与非关键负载直接串联所构成的整体称为智能负载，并与关键负载并联。当电网电压质量忽高忽低时，电力弹簧会输出电压改变非关键负载上的电流，进而将电网侧的“颠簸”全部转移，实时保证关键负载的电能质量。

三相电力弹簧可以被视为单向电力弹簧的扩展，每一相在三相电力弹簧中具有相同的拓扑结构。接下来将三相中的A相进行分析，拓扑结构如图2所示。

电力弹簧和非关键负载的串联支路被称为智能负载，关键负载和智能负载并联。当电网上的电压不稳定时，电力弹簧能够调节自身，输出不同的电压，改变流经非关键负载上的电流来将波动转移到了非关键的负载上，以此来保证关键负载的电压始终维持在参考值。通过对图2的分析，可以得知电压VES和电流iOA之间会形成相位差，因而电力弹簧不仅能够进行有功功率的转换，也可以向系统进行无功功率的转换。

图2中：RA和LA为A相的线路阻抗；VGA为A相的电网电压；VSA为A相的关键负载电压，同时也为A相母线电压；ViA为A相中逆变器输出电压；iA为A相输电线路上的电流；VOA为A相的非关键负荷的电压；iSA为A相关键负载的电流；VESA为A相电力弹簧输出的电压；iOA为A相非关键负载的电流；iLA为A相逆变器的输出电流。

4 仿真分析

本文根据图1所展示的三相电力弹簧结构图，搭建了一套三相电力弹簧并网仿真，通过仿真结果可以有效地验证本文所提出的无源控制策略的可行性和优越性。系统中各个元件的参数见表1。

本文模拟了4种工况下三相电力弹簧系统的运行情况来验证三相电力弹簧系统中各种情况下无源控制策略的性能，其中包含了三相电压平衡时输入的有功功率发生改变但其余参数保持不变、电网电压发生突变以及非关键负载电压发生改变时的3种工况以及当三相电压不平衡时三相电力弹簧减小三相电压不平衡的工况。此外，为了展示无源控制的优越性，将传统的PI控制仿真结果和本文提出的无源控制仿真结果进行对比。

根据电力弹簧的负载不同，所存在的工作模式也不同，但同一种控制方法可以实现对不同工作模式下的电力弹簧的控制。本文是对电力弹簧控制策略的研究，目的是提出一个可以解决电力弹簧协调的控制策略，又因提出的控制策略可以用于不同工作模式下的电力弹簧的控制，因而本文采用了简化的电力弹簧模型，关键负载和非关键负载均选取电阻模型。

4.1 工况1——系统的输入有功功率发生变化

为了验证输入的有功功率发生变化时，三相电力弹簧能否保证关键负载电压维持在参考值。现假设系统的有功功率初始值为2 000 W，在0.2 s的时候会突然变化为4 000 W，在0.3 s的时候又会重新变回到2 000 W。除此之外的所有参数均保持不变。

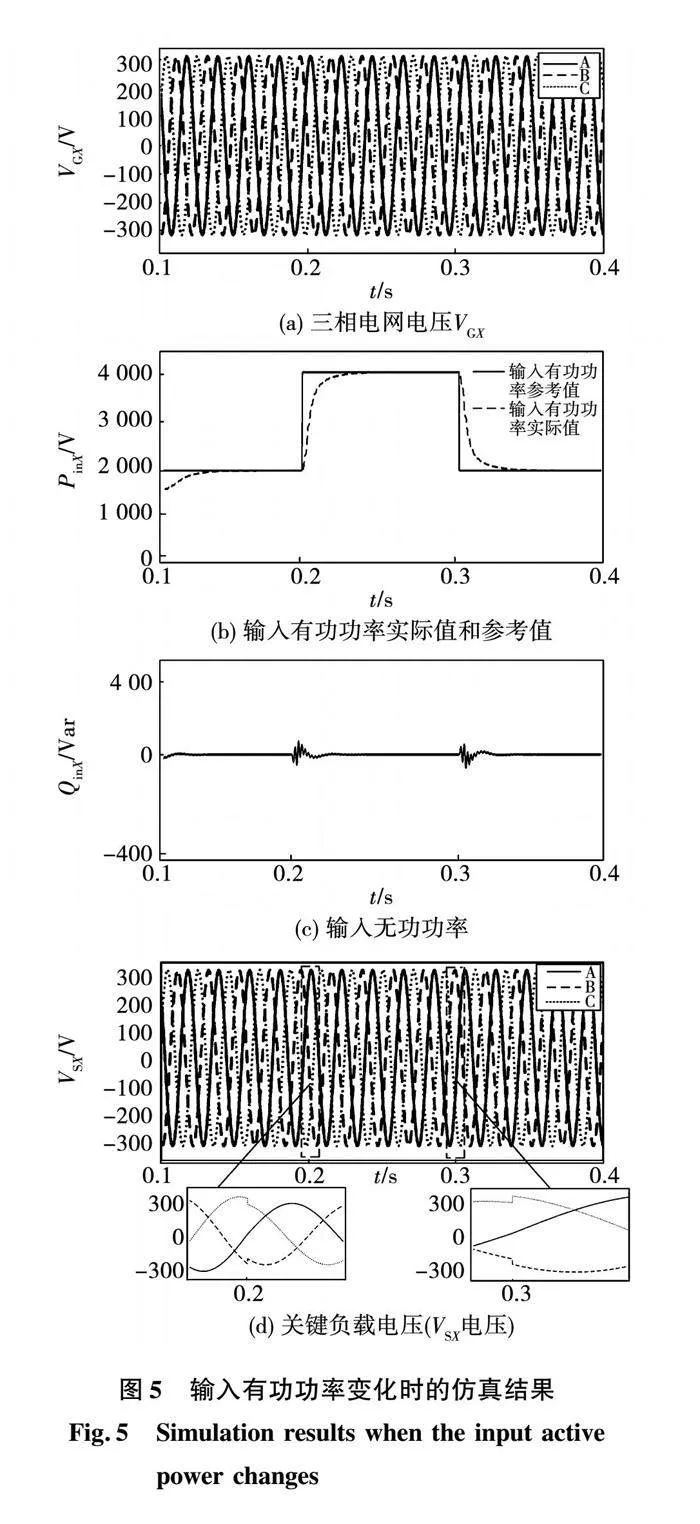
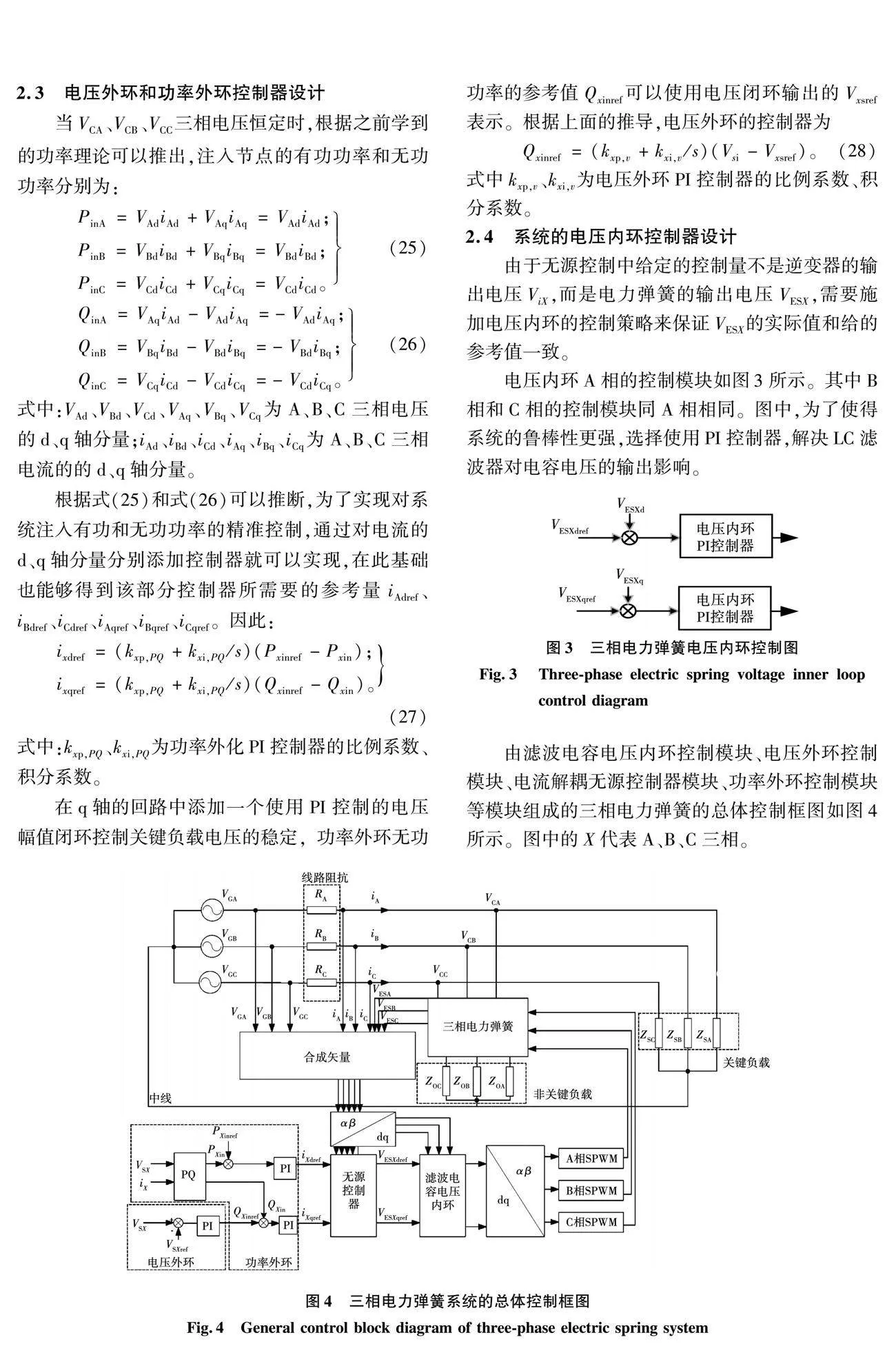
输入有功功率变化时系统的仿真结果如图5所示。其中：图5（a）为三相电网电压波形；图5（b）为实际输入的有功功率波形与参考有功功率波形；图5（c）为实际输入的无功功率波形；图5（d）为三相关键负载上电压波形。

根据仿真曲线可见，有功功率能够很好地动态跟随参考值，当输入有功功率发生变化时，电力弹簧会根据不同的情况输出不同的电压VESX，使得流经非关键负载上的电流发生改变，将电网的波动全部转移到了NCL上，以此来保持关键负载电压始终保持在有效值220 V（峰值为311 V）恒定。

4.2 工况2——系统的电网电压发生变化

为了验证系统电网电压发生变化时，三相电力弹簧能否保证关键负载电压维持在参考值。现在假设电网电压会在0.2 s时由311 V跌落至280 V，并在0.3 s的时候重新返回到311 V，在此过程中其余所有的参数均保持不变。

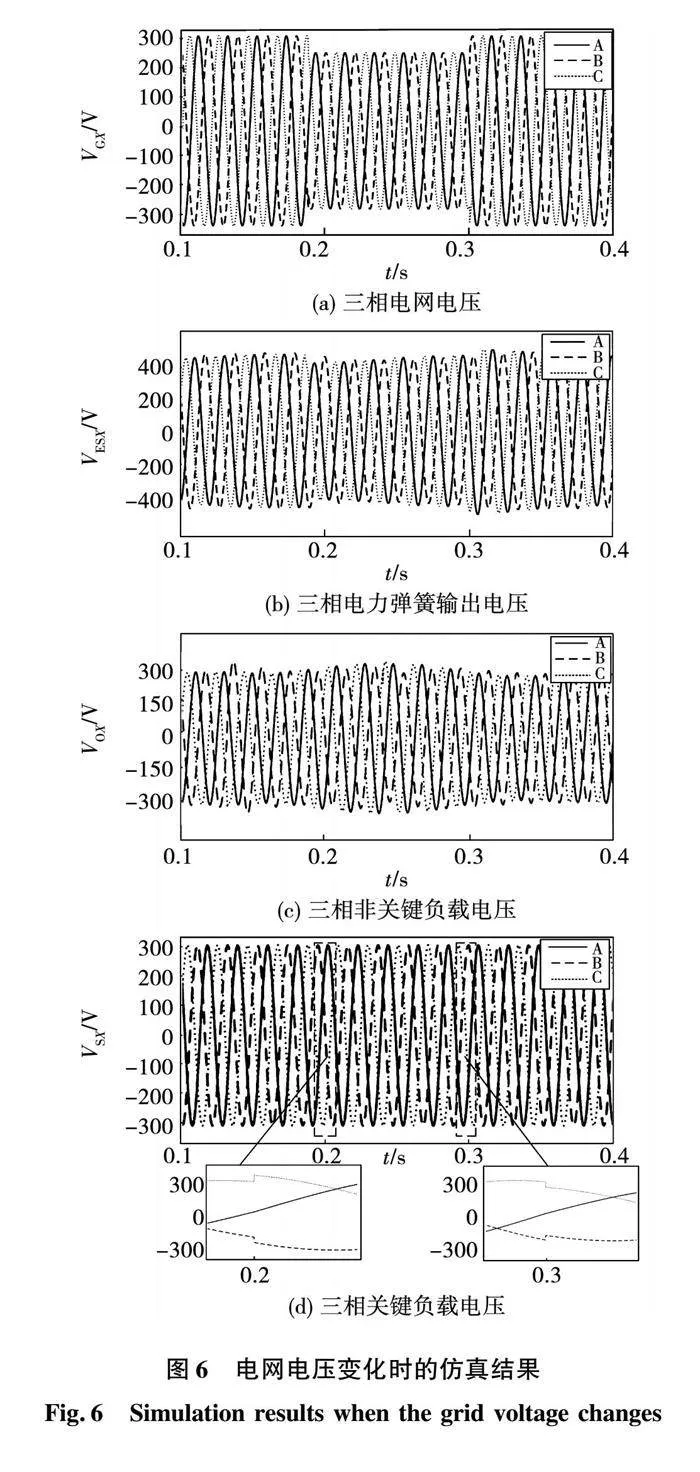
图6为电压变化时各参数波形的实验结果。其中：图6（a）为三相电网电压VGX波形；图6（b）为三相电力弹簧的输出电压VESX波形；图6（c）为三相非关键负载电压VOX波形；图6（d）为三相关键负载电压VSX波形。

由图6可见，当电网电压发生波动时，电力弹簧会根据电网电压改变的程度改变输出的电压，进而改变流经非关键负载的电流，将电网的波动转移到非关键负载上，以此来维持关键负载电压的稳定，保证关键负载电压一直处于稳定的状态。

4.3 工况3——系统的非关键负载发生变化

为了验证系统非关键负载发生变化时，三相电力弹簧能否保证关键负载电压维持在参考值。现在作出假设：非关键负载的阻值在0.2 s时由20 Ω变为40 Ω，并在0.3 s时重新回到20 Ω，在此过程中其余所有的参数均保持不变。

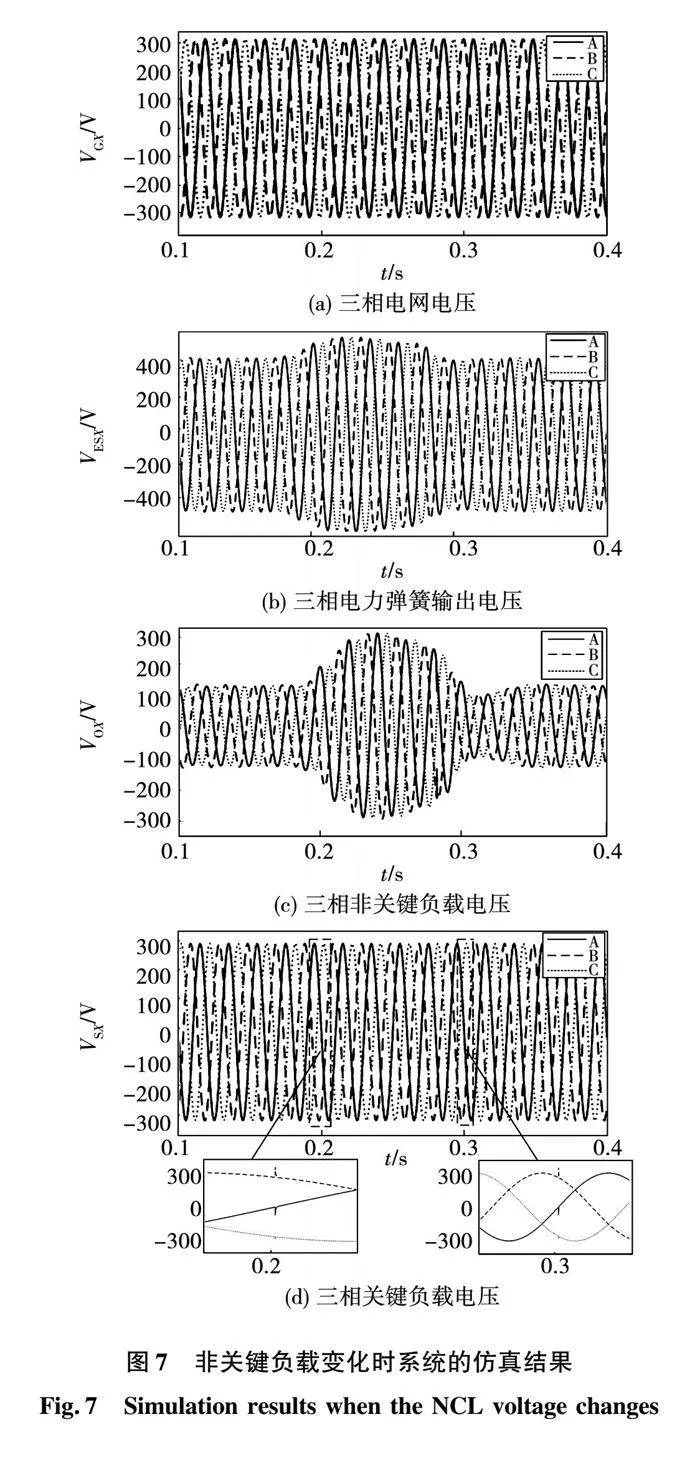
图7为非关键负载变化时各参数波形实验结果。其中：图7（a）为三相电网电压VGX波形；图7（b）为三相电力弹簧的输出电压VESX波形；图7（c）为三相非关键负载电压VOX波形；图7（d）为三相关键负载电压VSX波形。

根据得出的波形图可以看出，在非关键负载刚刚发生变化时，系统有功功率和无功功率在短时间内会发生波动，但在短暂的波动后仍然可以保持在参考值。三相电力弹簧的输出电压会相应的发生改变，进而使得智能负载上的电流也发生了相应的变化，使得非关键负载上的电压也随之发生相应的改变，将电路中的波动转移到了非关键负载上，以此来保证关键负载电压始终稳定在220 V。

4.4 工况4——三相不平衡下关键负载电压的平衡

为了模拟三相电力弹簧系统应对三相不平衡情况下的工况，在上面数据的基础上，将三相关键负载阻值分别调成50、70、60 Ω，其余所有的参数均保持不变。

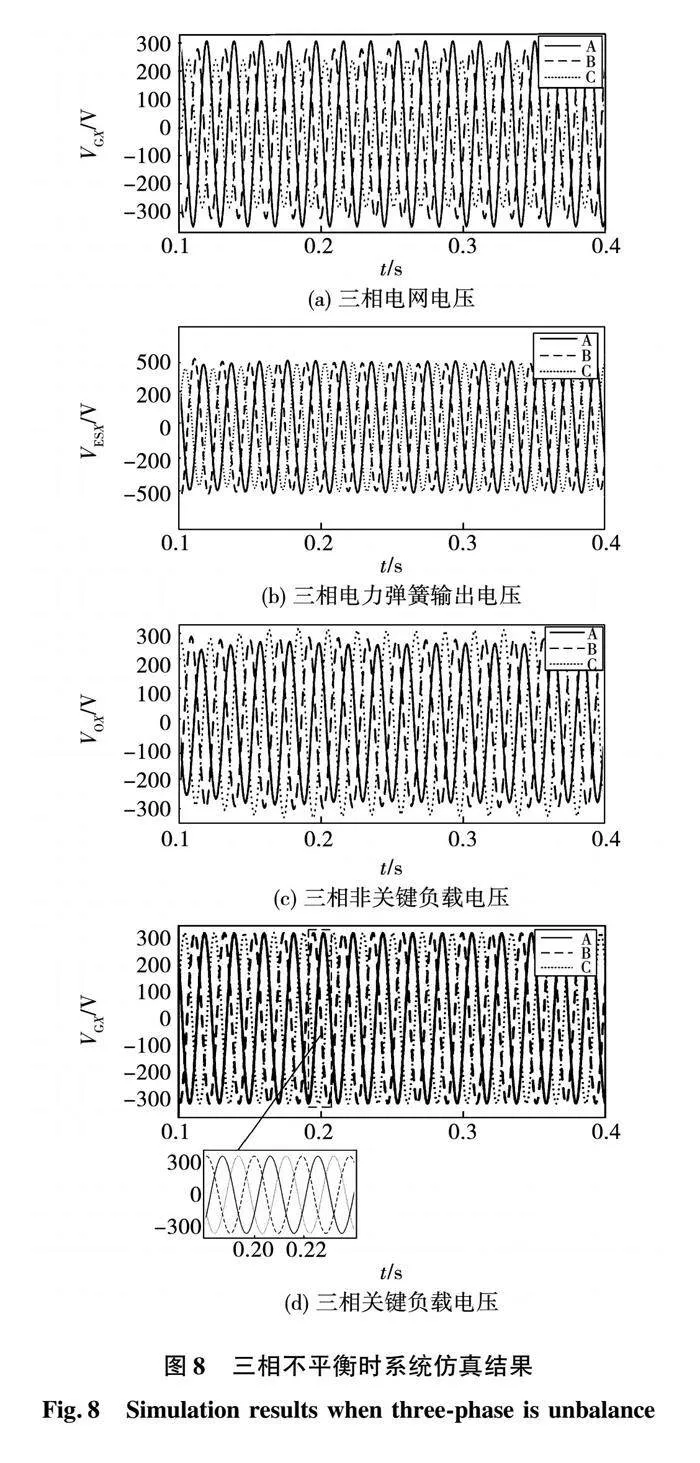
图8为三相不平衡电路中三相电力弹簧系统运行仿真波形。其中：图8（a）为三相电网电压VGX波形；图8（b）为三相电力弹簧的输出电压VESX波形；图8（c）为三相非关键负载电压VOX波形；图8（d）为三相关键负载电压VSX波形。

由图可见，由于三相关键负载阻值不同，造成每一相的电压均不相同，为了维持每一相上关键负载的电压相同，每一相的电力弹簧根据不同的情况，输出不同的电压，进而使每相的非关键负载电压也不相同，以此来保证三相关键负载电压的三相平衡与稳定。

4.5 本文的无源控制与传统的PI控制对比

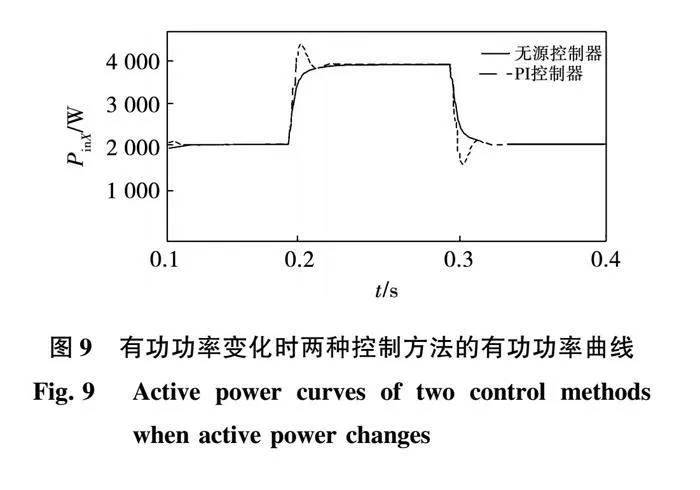
现将本文提出的无源控制与传统的PI控制进行比较，通过仿真对比体现出无源控制的优越性。图9为在功率变动的情况下两种控制策略的系统有功功率曲线。

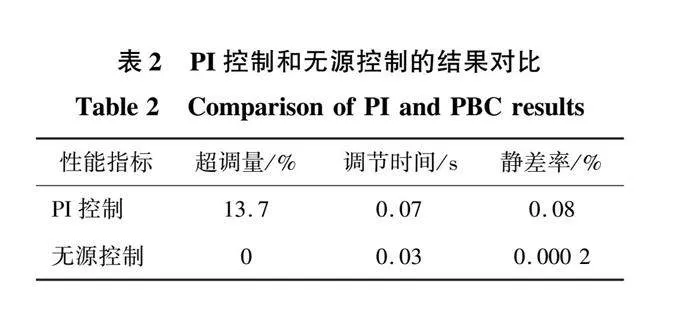
由曲线可见，在PI控制情况下，三相电力弹簧系统有功功率在跟随过程中会产生超调现象，且稳定的速度相对较慢；而本文所提的无源控制能够实现对有功功率参考值的快速追踪，且超调很小。表2为该系统的静态性能和动态性能分别在PI控制以及无源控制下控制指标对比结果。

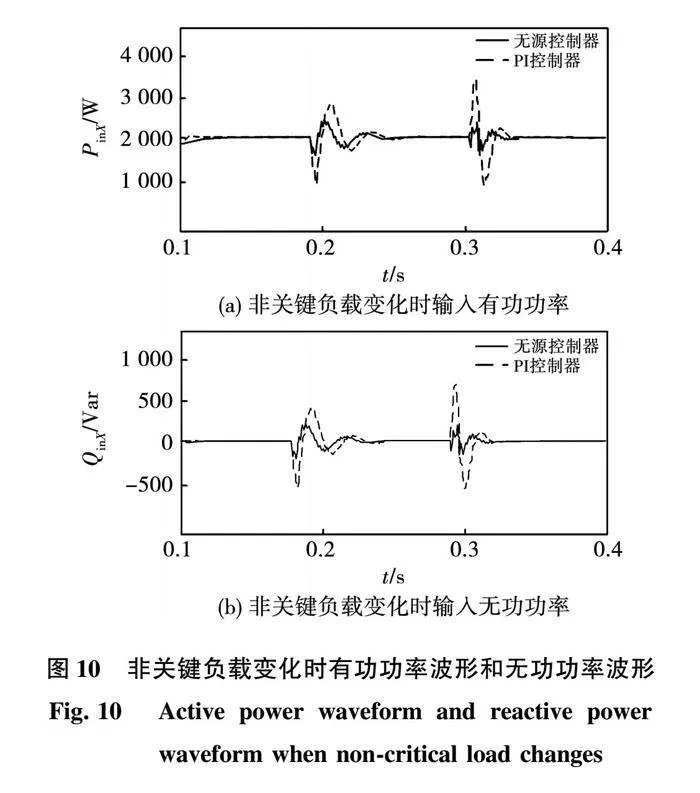
图10为在非关键负载变动工况下两种不同控制策略的系统功率对比曲线。从图中可以看出，在传统PI控制条件下有功功率和无功功率波动较大，且达到稳定时间较长；而无源控制则有着较小的功率波动，且能够较快地达到稳定。

根据表2和图9、图10的结果对比来看，与传统的线性PI控制相比，无源控制具有更快的动态响应速度、更小的稳态误差、更少的调节量以及更短的调节时间，无源控制在动态性能和静态性能方面表现更为出色。此外，相比于传统的PI控制，无源控制所需参数更少，控制系统结构更加简单。因此，相较于PI控制，无源控制有着更好的优越性。

5 实验分析

本文借助dSPACE系统，建立了图11所示的实验系统来验证无源控制（PBC）策略及其控制系统。提出的基于E-L模型的无源控制方法在Simulink环境下完成建模，同时也在RT-LAB实验平台上运行。为了将提出的无源控制方法自动转换并下载到dAPACE系统中，采用DS2201A/D，读取系统电压和电流用于直接测量相关参数实时监控的Control Desk软件，以及用于形成PWM信号以做到调制的DS40002FTOD的。DSPTMS320F28335是一款适用于逆变器控制高速处理器，能够直接将硬件连接到MATLAB/Simulink仿真模型环境，将算法编译并转换为C语言代码，然后加载到实时DSPTMS320F28335处理器上。

选取上述工况中最复杂的工况，即4.4节三相不平衡的工况（也即模拟三相电力弹簧系统应对三相电压不平衡工况），将三相关键负载阻值分别调成50、60、70 Ω，其余参数保持不变。

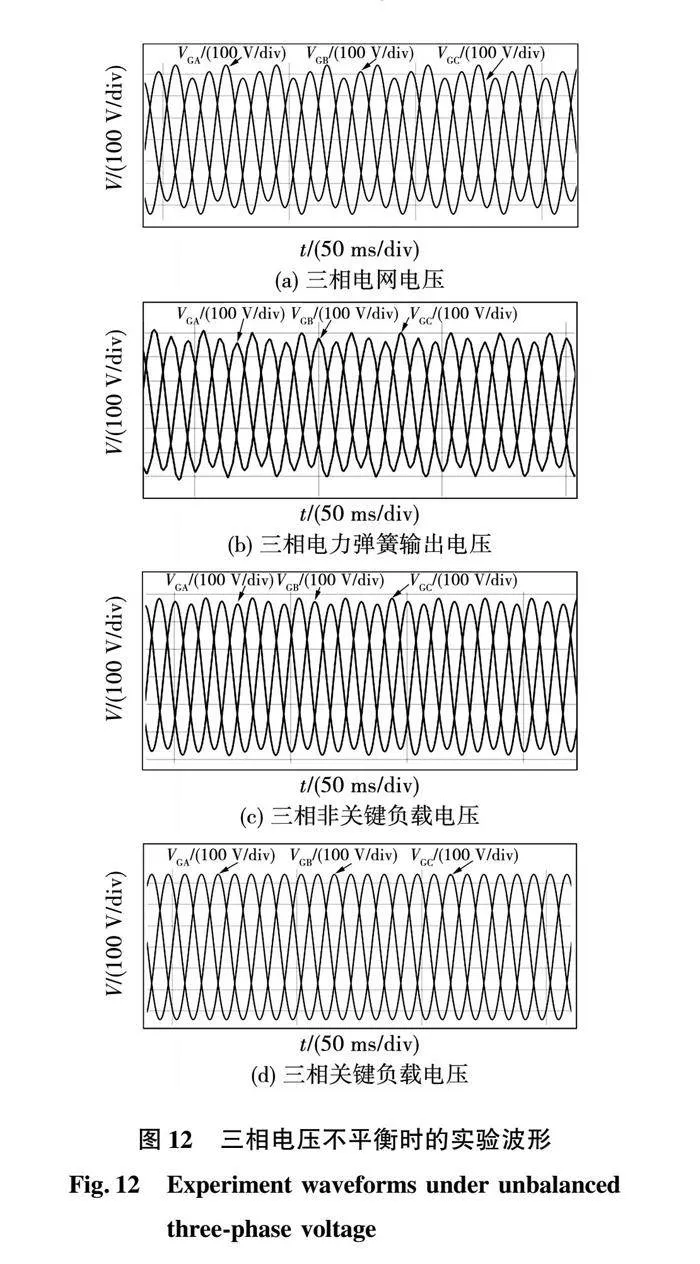
图12为4.4节工况下三相电压不平衡时三相电力弹簧系统实验结果。其中，图12（a）、图12（b）、图12（c）、图12（d）分别为三相电网电压VGX、三相电力弹簧的输出电压VESX、三相非关键负载电压VOX、三相关键负载电压VSX。

由图12可见，在三相不平衡的电路中，每相的电网电压不相同，根据每相电网电压的不同电压值，三相电力弹簧会输出不同的电压，进而调整非关键负载上的电流，将电网侧的“颠簸”全部由非关键负载承担，进而保证三相关键负载上的电压相同，很好地解决了三相不平衡的问题。

由实验结果可见，所提出的基于无源控制的三相电力弹簧能够解决三相不平衡电路的问题，维持关键负载电压的平稳，动、静态性能较优，且实验结果与仿真结果一致。

6 结 论

本文通过理论以及相关的实验验证了将基于E-L模型的无源控制策略应用在三相电力弹簧系统中的有效性和优越性，并进一步地得出了以下结论：

1）当系统非关键负载发生变化或者电网电压发生波动或输入的有功功率改变时，三相电力弹簧在使用无源控制时，可以很好地稳定关键负载上的电压。

2）在三相不平衡电路中，应用本文提出的无源控制的三相电力弹簧系统也可以一定程度上降低三相不平衡的问题。

3）对于三相电力弹簧等强非线性系统来说，根据仿真以及实验的结果来看，无源控制比PI控制更加适用。因为无源控制具有更快的动态速度和更低的谐波含量、鲁棒性也更强、抗干扰能力更加优秀、需要调节的相关参数少，整体的控制效果更优秀。

参 考 文 献：

［1］ 李帛洋， 晁璞璞， 李卫星， 等. 风电经特高压直流送出系统的暂态过电压计算方法［J］. 电机与控制学报， 2021， 25（21）： 11.

LI Boyang， CHAO Pupu， LI Weixing， et al. Transient overvoltage calculation method of wind power transmission system via UHVDC［J］. Electric Machines and Control， 2021， 25（12）： 11.

［2］ 王鑫， 杨德建. 基于变系数PI控制的双馈风电机组自适应转速恢复策略［J］. 电工技术学报， 2023， 38（15）： 4120.

WANG Xin， YANG Dejian. Adaptive speed recovery strategy of doubly-fed induction generator based on variable PI control coefficient［J］. Transactions of China Electrotechnical Society， 2023， 38（15）： 4120.

［3］ 刘畅， 卓建坤， 赵东明， 等. 利用储能系统实现可再生能源微电网灵活安全运行的研究综述［J］. 中国电机工程学报， 2020， 40（1）： 1.

LIU Chang， ZHUO Jiankun， ZHAO Dongming， et al. A review on the utilization of energy storage system for the flexible and safe operation of renewable energy microgrids［J］. Proceedings of the CSEE， 2020， 40（1）： 1.

［4］ 袁志昌， 郭佩乾， 刘国伟， 等. 新能源经柔性直流接入电网的控制与保护综述［J］. 高电压技术， 2020， 46（5）： 1460.

YUAN Zhichang， GUO Peiqian， LIU Guowei， et al. Review on control and protection for renewable energy integration through VSC-HVDC［J］.High Voltage Engineering，2020，46（5）：1460.

［5］ HUI S Y R， LEE C K， WU F F. Electric rings-a new smart grid technology［J］. IEEE Transactions on Smart Grid， 2012， 3（3）： 1552.

［6］ 尹发根， 王淳.电力弹簧研究进展： 原理、拓扑结构、控制和应用［J］. 电网技术， 2019， 43（1）： 174.

YIN Fagen， WANG Chun. Review of electric spring： Principle， topologies， control and applications［J］. Power System Technology， 2019， 43（1）： 174.

［7］ LEE C K， CHAUDHURI B， HUI S Y. Hardware and control implementation of electric springs for stabilizing future smart grid with intermittent renewable energy sources［J］. IEEE Journal of Emerging amp; Selected Topics in Power Electronics，2013，1（1）：18.

［8］ TAN S C， LEE C K， HUI S Y R. General steady-state analysis and control principle of electric springs with active and reactive power compensations［J］. IEEE Transactions on Power Electronics， 2013， 28（8）： 3958.

［9］ MOJTABA M S， TURAJ A. Hybrid AC/DC transmission expansion planning considering HVAC to HVDC conversion under renewable penetration［J］. IEEE Transactions on Power Systems， 2021， 36（1）： 579.

［10］ ZENG Xiangjun， GONG Deling， WEI Milan， et al. Research on novel hybrid multilevel inverter with cascaded H-bridges at alternating current side for high-voltage direct current transmission［J］. IET Power Electronics， 2018， 11（12）： 1914.

［11］ LUO Jiajie， ZHANG Xiaoping， XUE Ying， et al. Harmonic analysis of modular multilevel matrix converter for fractional frequency transmission system［J］. IEEE Transactions on Power Delivery， 2020， 35（3）： 1209.

［12］ AKHTAR Z， CHAUDHURI B， HUI S Y R. Smart loads for voltage control in distribution networks［J］. IEEE Transactions on Smart Grid， 2017， 8（2）： 937.

［13］ MA Jiankai， DAHIDAH M， PICKERT V， et al. Modular multilevel matrix converter for offshore low frequency AC transmission system［C］// 2017 IEEE 26th International Symposium on Industrial Electronics（ISIE）， August 3， 2017， Edinburgh， Scotland， United Kingdom. 2017： 768-774.

［14］ MORA A， ESPINOZA M， DIAZ M， et al. Control of wind energy conversion systems based on the modular multilevel matrix converter［J］. IEEE Transactions on Industrial Electronics， 2017， 64（11）： 8799.

［15］ ZHANG Chong， JIANG Daozhuo， ZHANG Xuan， et al .The study of a battery energy storage system based on the hexagonal modular multilevel direct AC/AC converter （Hexverter）［J］. IEEE Access， 2018， 6： 43343.

［16］ ROBLES-CAMPOS H R， MANCILLA-DAVID F. A comparative evaluation of modulation strategies forhexverter-based modular multilevel converters［C］//Proceedings of the IEEE International Conference on Industrial Technology （ICIT）， February 1， 2019， Melbourne， VIC， Australia. 2019： 1465-1470.

［17］ WANG Q S， CHENG M， JIANG Y L， et al. A simple active and reactive power control for applications of single-phase electric springs［J］. IEEE Transactions on Industrial Electronics， 2018， 65（8）： 6291.

［18］ YU Ting， MENG Yongqing， YU Jianyang. Control scheme of Y-connected modular multilevel converter in fractional frequency transmission system under unbalanced grid fault［C］//IEEE 8th International Conference on Advanced Power System Automation and Protection （APAP）， October 21， 2019， Xi’an， China. 2019： 720-724.

［19］ 游建章， 郭谋发. 含四桥臂H桥变流器的不对称配电网综合补偿方法［J］. 电工技术学报， 2022， 37（11）： 2849.

YOU Jianzhang， GUO Moufa. Comprehensive compensation method for asymmetric distribution network with four arm H-bridge converter［J］. Transactions of China Electrotechnical Society， 2022， 37（11）： 2849.

［20］ ZHAO Xiaomin， YANG Bingyuan. Coordinated control strategy based on MMC and DFIG［C］// International Conference on Environment Science and Advanced Energy Technologies（ESAET），January 18，2020，Chongqing，China.2020：1549-1555.

［21］ LIU Shenquan， SAEEDIFARD M， WANG Xifan， et al. A current reallocation strategy to attenuate the peak arm current of the modular multilevel matrix converter［J］. IEEE Journal of Emerging and Selected Topics in Power Electronics，2019，7（4）： 2292.

［22］ 黄敏， 陈凡， 吴卫民， 等. 弱电网下无锁相环的并网逆变器无源控制策略［J］. 电机与控制学报， 2022， 26（3）： 127.

HUANG Min， CHEN Fan， WU Weimin， et al. Passivity-based. control of grid-connected inverters without phase-locked loop under weak grid［J］. Electric Machines and Control， 2022， 26（3）： 127.

［23］ 程明， 王青松， 张建忠. 电力弹簧理论分析与控制器设计［J］. 中国电机工程学报， 2015， 35（10）： 2436.

CHENG Ming， WANG Qingsong， ZHANG Jianzhong. Theoretical analysis and controller design of electric springs［J］. Proceedings of the CSEE， 2015， 35（10）： 2436.

［24］ 鲍克勤， 吴浩强， 程启明， 等. 基于E-L模型的电力弹簧无源控制策略［J］. 高电压技术， 2022， 48（12）： 4986.

BAO Keqin， WU Haoqiang， CHENG Qiming， et al. Passive-based control strategy of electric springs based on E-L model［J］. High Voltage Engineering， 2022， 48（12）： 4986.

（编辑：刘素菊）