表贴式轴向磁通电机梯形削极分段结构研究

摘 要：

采用多极少槽结构和分数槽集中绕组可有效提高轴向磁通永磁（AFPM）电机的转矩密度，但磁动势谐波含量较大、频率较高，会引起永磁体涡流损耗增大和温度升高。通过优化表贴式轴向磁通永磁电机的永磁体结构可有效降低永磁体涡流损耗并抑制转矩波动，因此提出梯形削极分段结构。首先，基于精确子域法分别建立不同永磁体结构的解析模型。其次，通过解析模型和三维有限元模型对不同永磁体结构的气隙磁密、输出转矩和涡流损耗进行分析对比。然后，通过研究永磁体分段对永磁体涡流损耗的影响，确定梯形削极分段结构的参数。最后，制造一台样机并进行实验，实验结果证明，梯形削极分段结构可有效降低永磁体涡流损耗并且改善轴向磁通永磁电机输出性能。

关键词：轴向磁通永磁电机；梯形削极分段结构；永磁体结构；永磁体涡流损耗；转矩密度；精确子域法

DOI：10.15938/j.emc.2024.03.009

中图分类号：TM351

文献标志码：A

文章编号：1007-449X（2024）03-0084-12

收稿日期： 2023-08-09

基金项目：国家自然科学基金面上项目（51877139）；辽宁省教育厅科学研究经费项目（面上项目）（LJKZ0128）

作者简介：武 岳（1995—），男，博士，研究方向为轴向磁通永磁电机设计、控制及多物理场分析；

张志锋（1981—），男，博士，教授，博士生导师，研究方向为高功率密度电推进系统、特种电机设计及其控制;

张 冉（1991—），男，硕士，工程师，研究方向为电驱动产品总体设计。

通信作者：张志锋

Trapezoidal shaping segmented structure of surface mount axial flux permanent magnet motor

WU Yue1， ZHANG Zhifeng1， ZHANG Ran2

（1.School of Electrical Engineering， Shenyang University of Technology， Shenyang 110870， China;2.Beijing Institute of Space Launch Technology， Beijing 100076， China）

Abstract：

The torque density of axial flux permanent magnet （AFPM） motor can be improved effectively by adopting multi-pole and few-slot structure， and fractional slot concentrated winding， but the large harmonic content of magnetomotive force and the high frequency will lead to the increase of permanent magnet eddy current loss and temperature rise. By optimizing the permanent magnet structure of the surface mount AFPM motor， the permanent magnet eddy current loss can be effectively reduced and the torque ripple can be suppressed. Therefore， the trapezoidal shaping segmented permanent magnet structure was proposed. Firstly， the analytical models of different permanent magnet structures were established based on the precise subdomain method. Secondly， the air gap magnetic flux density， output torque and eddy current loss of different permanent magnet structures were analyzed and compared by analytical model and three-dimensional finite element model. Then， the structure parameters of trapezoidal shaping segmented permanent magnet structure were determined by studying the effect of permanent magnet segmented on eddy current loss. Finally， a prototype was manufactured and tested. The experimental results prove that the trapezoidal shaping segmented permanent magnet structure can effectively reduce the permanent magnet eddy current loss and improve the output performance of the AFPM motor.

Keywords：axial flux permanent magnet motor; trapezoidal shaping segmented structure; permanent magnet structure; permanent magnet eddy current loss; torque density; precise subdomain method

0 引 言

随着大力推动航空航天、船舶及新能源汽车等行业创新绿色发展，电机领域相关技术的要求不断提高，电机逐渐呈现出向高转矩密度和节能等方向发展［1-3］。轴向磁通永磁（axial flux permanent magnet，AFPM）电机具有高转矩密度和结构紧凑等明显的优势，已经成为电机领域的研究热点［4-6］。AFPM电机的拓扑结构异常丰富，其中双转子单定子AFPM电机被广泛应用［7］。采用多极少槽结构和分数槽集中绕组可进一步提高双转子单定子AFPM电机的转矩密度，但也会引起较大的转矩波动和永磁体涡流损耗。因此，降低此类电机的转矩波动和永磁体涡流损耗是必要的［8］。

对于表贴式双转子单定子AFPM电机而言，气隙磁密波形与永磁体形状密切相关，通过合理优化永磁体结构，可以有效地减小气隙磁密中的谐波含量，抑制转矩波动与电机的涡流损耗，从而提高电机的转矩密度，改善电机输出性能［9-10］。文献［11］分析了永磁体的充磁方向和永磁体的斜边角对气隙磁密谐波含量的影响，采用降低气隙磁密谐波含量的方法来减小定子铁心的涡流损耗。文献［12］提出每极采用材料相同、厚度和宽度不等的多块永磁体组合而成的磁极，通过此方法可降低磁势的谐波含量和削弱气隙磁密中的谐波含量，但是多块不等宽、不等厚的永磁体结构会增加加工难度和安装难度。文献［13］设计一种采用梯形Halbach永磁体结构的无铁心AFPM电机，在相同永磁体用量下，梯形永磁体结构的气隙磁密基波幅值可增加5.37%，3次、5次谐波含量减少。通过合理增加主磁极的厚度、优化辅助磁极结构，可有效改善电机气隙磁密的分布。但在Halbach永磁体结构中，永磁体具有多个充磁方向，确定最佳的充磁方向较为困难，同时这种梯形Halbach永磁体结构较复杂，会增加制造成本和工艺难度。文献［14］对一台12槽10极电机永磁体在正弦削极下的边缘厚度进行分析和优化，结果表明永磁体边缘厚度为1 mm时，气隙磁场谐波含量最小。但正弦削极会使永磁体利用率低，造成气隙磁密基波幅值下降严重，导致输出性能下降。

文献［15］分析了碳纤维素保护环和钛合金保护环对永磁体涡流损耗的影响，实验结果证明采用碳纤维素保护环可以有效降低永磁体涡流损耗。文献［16］提出采用电镀铜的方式来降低一台轴向无铁心永磁电机的永磁体涡流损耗。文献［17-18］详细研究了永磁体分段对永磁体涡流损耗的影响，仿真结果证明永磁体分段是一种非常有效的方法，但是确定最佳的永磁体分段数量是一个难点。

综上所述，针对以上问题，本文对AFPM电机的永磁体结构进行优化，提出梯形削极分段结构。首先，基于精确子域法建立不同永磁体削极结构的解析模型。其次，基于解析模型和三维有限元分析削极角度对梯形削极结构的影响，并且对比不同永磁体削极结构对磁场和涡流损耗的影响。然后，研究永磁体分段对永磁体涡流损耗的影响，确定梯形削极分段结构的参数。最后，基于样机实验进行验证。

1 轴向磁通永磁电机结构及不同削极永磁体结构

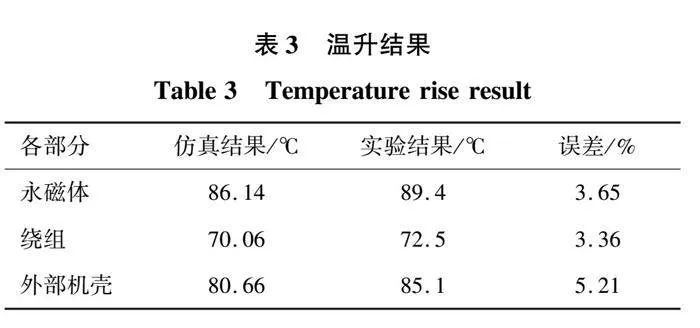
本文将一台额定功率为55 kW、额定转速为2 500 r/min的双转子单定子AFPM电机作为研究载体，其拓扑结构如图1所示。为了提高电机转矩密度，定子采用无轭部模块化结构，该结构可以减轻定子铁心重量，降低定子铁心损耗。电机还采用分数槽集中绕组，可以减小绕组端部长度，降低绕组铜耗。

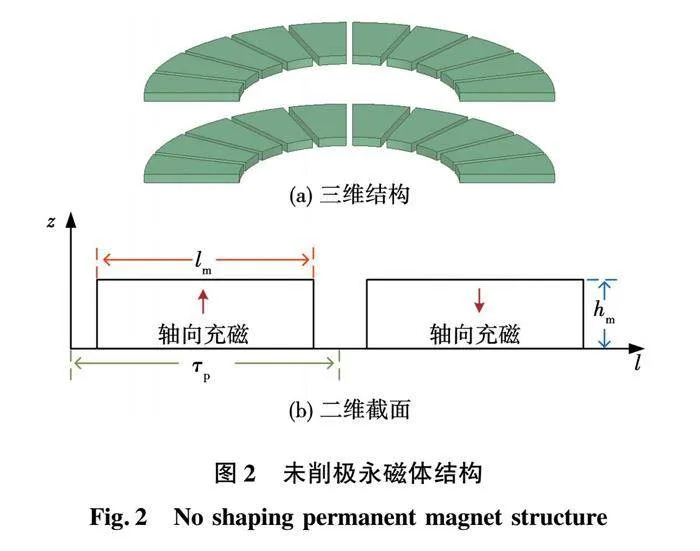
对于表贴式永磁电机，永磁体削极技术是改善电机电磁性能的有效手段。本文将对扇形永磁体结构进行削极，各种削极结构的轴向投影均保持扇形形状。图2（a）是未削极永磁体的三维结构，其沿着周向的截面为矩形，如图2（b）所示。图中：lm是永磁体长度；τp是永磁体极距；hm是永磁体沿着轴向的厚度。

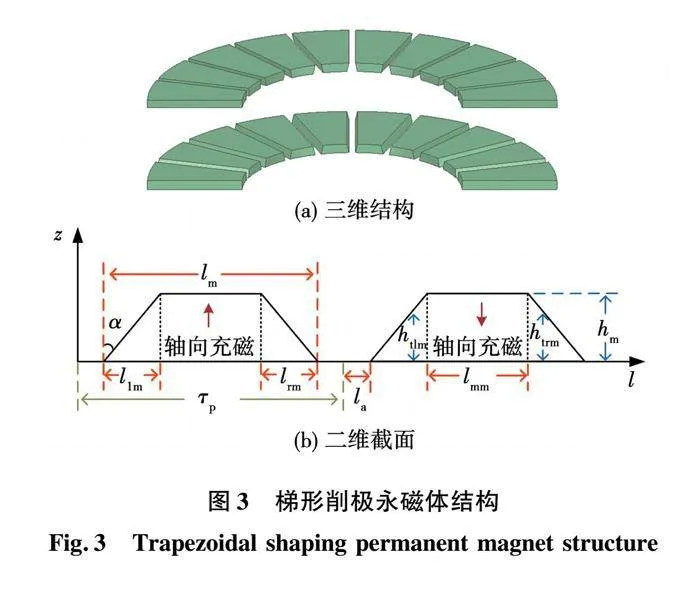
图3（a）是本文提出的梯形削极永磁体三维结构，其沿着周向的截面为梯形，如图3（b）所示。在梯形削极永磁体中，其形状与削极角度α有关，并且其永磁体轴向充磁厚度不再恒定不变。为了分析削极角度对永磁体的影响，梯形削极永磁体将分为左、中和右三部分进行求解。左、右两部分的削极角度相同，而且当削极角度确定时，左部分的永磁体轴向充磁厚度htlm和右部分的永磁体轴向充磁厚度htrm都随着周向位置的变化而改变。分别求解得到各部分永磁体的磁化强度，然后通过叠加法合成最终磁化强度。最后，根据边界条件求解电机的磁场，从而获得相关电磁性能。图中：llm是梯形削极左部分的永磁体长度；lrm是梯形削极右部分的永磁体长度；lmm是梯形削极中间部分的永磁体长度；la是梯形削极永磁体半极间长度。

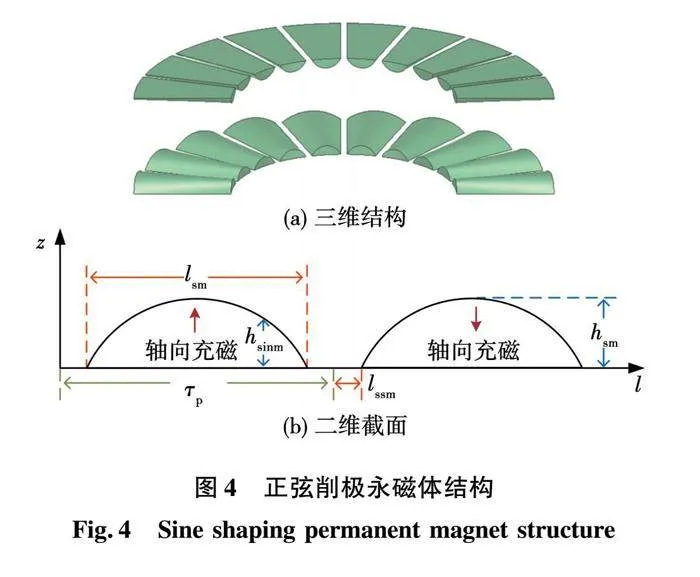
正弦削极是常见的永磁体削极技术，为了对比不同削极结构对电机性能的影响，本文将对未削极永磁体结构、梯形削极永磁体结构和正弦削极永磁体结构进行详细对比。图4（a）是正弦削极永磁体的三维结构，其沿着周向的截面为正弦波形，如图4（b）所示。图中：hsm是正弦削极永磁体沿着轴向的最大厚度；hsinm是与周向位置有关的正弦削极永磁体轴向充磁厚度；lssm是正弦削极永磁体半极间长度。

2 不同永磁体结构的精确子域解析模型及永磁体涡流损耗研究

2.1 精确子域解析模型建立

将AFPM电机的三维模型在平均半径处沿周向展开成二维切片模型，基于极坐标建立不同削极结构的精确子域解析模型，如图5所示。为了简化解析模型，以槽中心为分割线，建立单侧结构的解析模型。

图5（a）为未削极永磁体结构的精确子域模型，图5（b）为梯形削极永磁体结构的精确子域模型，图5（c）为正弦削极永磁体结构的精确子域模型。图中解析模型被分成4个子域，永磁体区域为子域1，气隙区域为子域2，定子槽区域为子域3i，定子槽口区域为子域4i，i为定子槽序号。θ方向和z方向分别表示AFPM电机的周向和轴向，hr是转子铁心沿着轴向的厚度，hδ是气隙长度。以梯形削极永磁体结构为例，推导各个子域方程。

3 不同永磁体结构磁场及涡流损耗分析

3.1 不同削极角度对梯形削极永磁体磁场的影响

为了确定梯形削极永磁体最佳的削极角度，将以负载气隙磁通密度总谐波畸变率（total harmonic distortion，THD）、电磁转矩和转矩波动为目标，对不同削极角度的AFPM电机进行分析。在永磁体结构的优化过程中，应保持梯形削极永磁体左右两部分的削极角度相等，永磁体中间部分的充磁厚度与极弧系数保持与未削极之前相同。不同削极角度下的负载气隙磁密THD、电磁转矩和转矩波动可以根据精确子域法计算的负载气隙磁密进行求解。为了验证解析计算的正确性，对一台额定功率为55 kW的AFPM电机进行三维有限元分析。

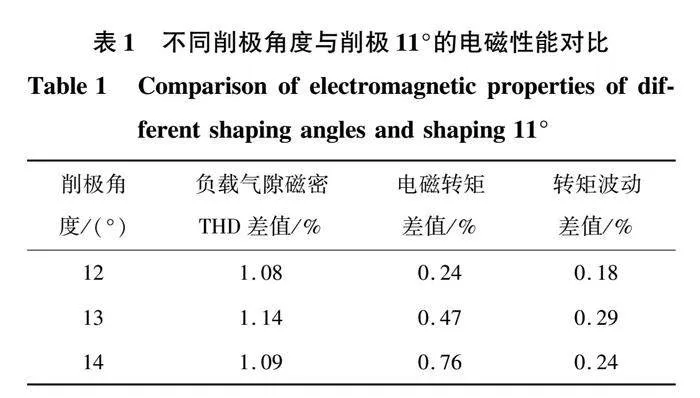
图7为梯形削极永磁体在不同削极角度下的负载气隙磁密THD，可以看出，两种计算方法的吻合度较高。随着增加削极角度，负载气隙磁密THD先减小后增加。首先，削极角度在5°～25°范围内，每隔5°取一个值，计算对应的负载气隙磁密THD，可以看出在10°～15°范围内，负载气隙磁密THD较小。然后，在此范围内，每隔1°取一个值，计算对应的负载气隙磁密THD。当削极角度为11°、12°、13°和14°时，负载气隙磁密THD分别为19.44%、18.36%、18.30%和18.35%。

图8为梯形削极永磁体在不同削极角度下的电磁转矩，可以看出，两种计算方法的吻合度较高。随着增加削极角度，电磁转矩持续下降，并且下降的趋势逐渐增加。因为梯形削极永磁体的上边长度与削极角度的正切函数成正比，随着削极角度增加，永磁体体积呈非线性减小且下降趋势逐渐增加。与负载气隙磁密THD选择参数范围相同，当削极角度为11°、12°、13°和14°时，电磁转矩分别为210.5、210、209.5和208.9 N·m。

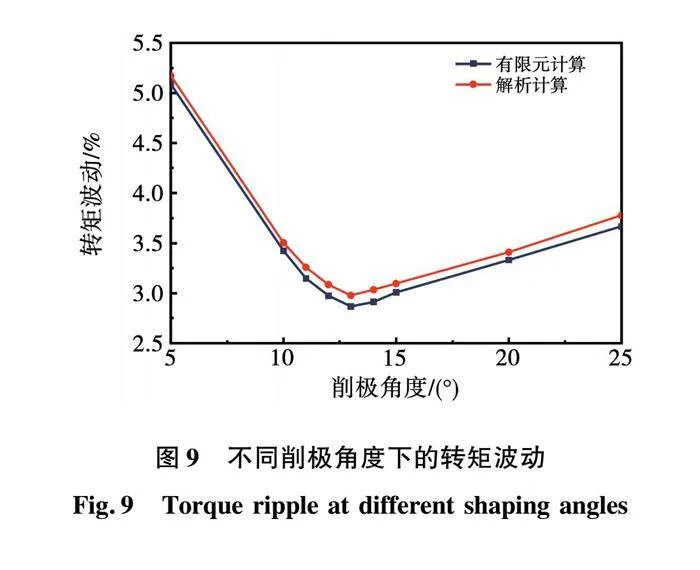
图9为梯形削极永磁体在不同削极角度下的转矩波动，可以看出，两种计算方法的吻合度较高。随着增加削极角度，转矩波动先减小后增加，其变化的趋势与负载气隙磁密THD变化的趋势相同。与负载气隙磁密THD选择参数范围相同，当削极角度为11°、12°、13°和14°时，转矩波动分别为3.15%、2.97%、2.86%和2.91%。

将不同削极角度与削极11°的电磁性能进行对比，如表1所示。其中，负载气隙磁密THD差值与转矩波动差值越大越好，电磁转矩差值越小越好。从表中可以看出，削极13°的负载气隙磁密THD差值与转矩波动差值均最大，虽然电磁转矩差值不是最小值，但是与最小值相差不大。因此，综合考虑负载气隙磁密THD、电磁转矩和转矩波动，最终确定梯形削极永磁体的削极角度为13°。

3.2 不同永磁体削极结构磁场对比

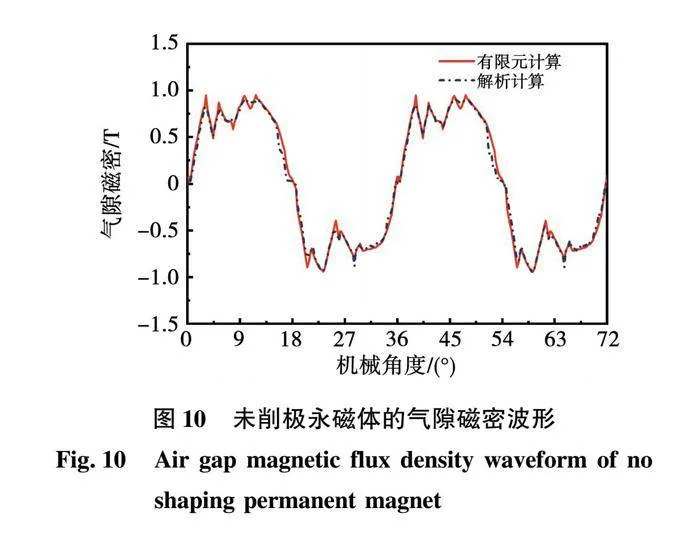
为了确定最佳的永磁体削极结构，将对不同永磁体削极结构的电磁性能和永磁体涡流损耗进行对比分析。图10为未削极永磁体的气隙磁密波形，可以看出，两种方法的吻合度较高，未削极永磁体的气隙磁密THD为31.90%。

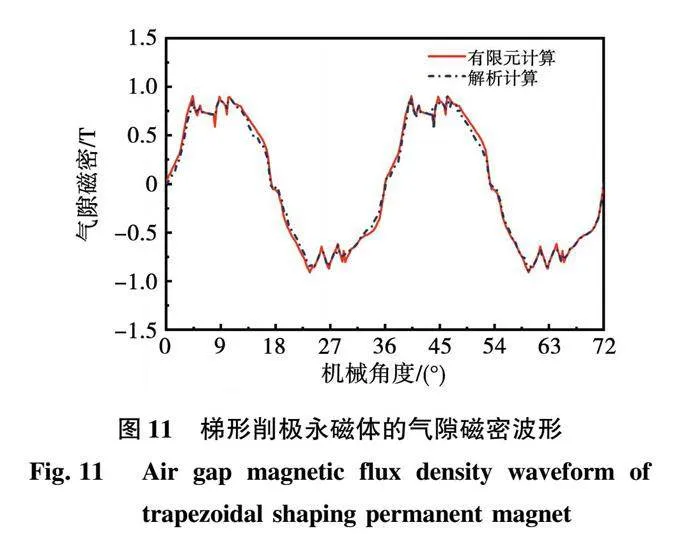
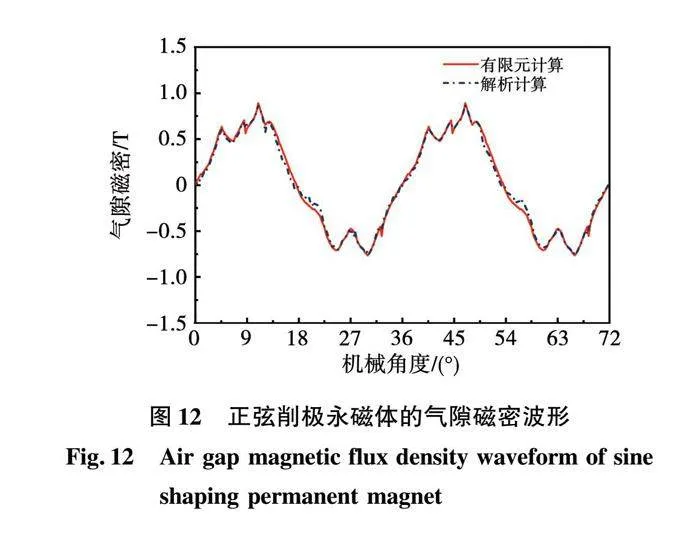
图11为梯形削极永磁体的气隙磁密波形，可以看出，两种方法的吻合度较高，梯形削极永磁体的气隙磁密THD为18.30%。与未削极永磁体相比，梯形削极永磁体的气隙磁密THD下降了13.6%。图12为正弦削极永磁体的气隙磁密波形，可以看出，两种方法的吻合度较高，正弦削极永磁体的气隙磁密THD为17.26%。与未削极永磁体相比，正弦削极永磁体的气隙磁密THD下降了14.64%。

图13为额定工况下未削极永磁体的电磁转矩波形，转矩波动为6.19%，电磁转矩的有限元计算值与解析计算值分别为213.2和204.8 N·m，误差为3.94%。

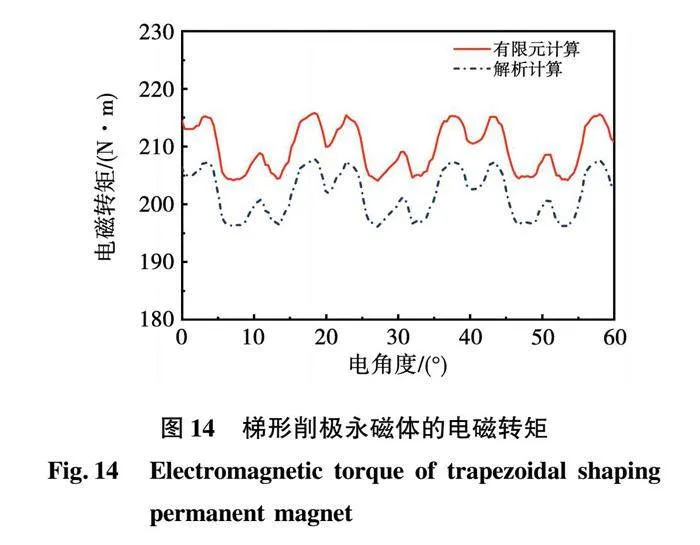
图14为额定工况下梯形削极永磁体的电磁转矩波形，可以看出，转矩波动为2.86%，电磁转矩的有限元计算值与解析计算值分别为209.5和201.3 N·m，误差为3.91%。与未削极永磁体相比，电磁转矩下降了1.74%，转矩波动下降了3.33%。

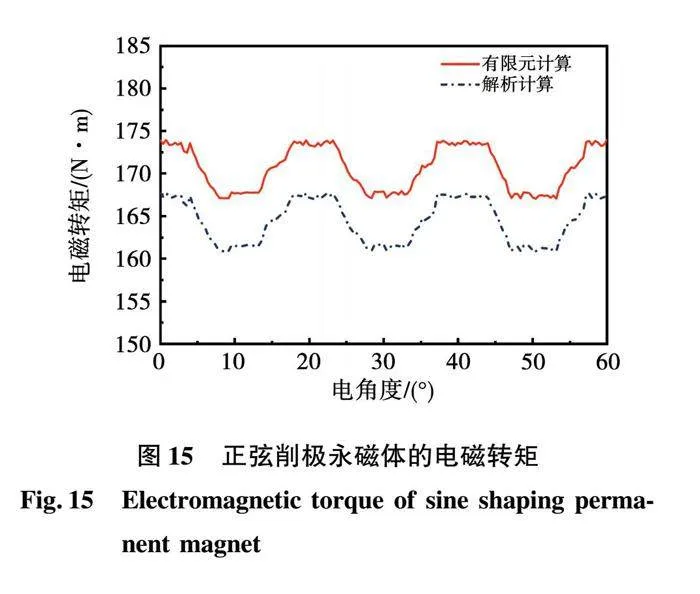
图15为额定工况下正弦削极永磁体的电磁转矩波形，可以看出，转矩波动为1.98%，电磁转矩的有限元计算值与解析计算值分别为170.6和164 N·m，误差为3.86%。与未削极永磁体相比，电磁转矩下降了19.98%，转矩波动下降了4.21%。

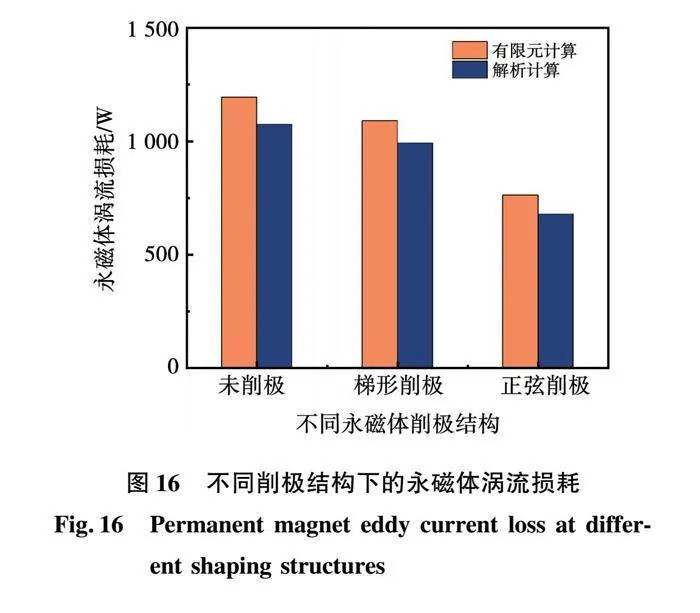
图16为不同削极结构下的永磁体涡流损耗，其中未削极永磁体结构的永磁体涡流损耗的有限元计算值和解析计算值分别为1 193.95和1 073.56 W，误差为10.08%。梯形削极永磁体结构的永磁体涡流损耗的有限元计算值和解析计算值分别为1 089.68和990.61 W，误差为9.09%。与未削极永磁体结构相比，其永磁体涡流损耗下降了8.73%。正弦削极永磁体结构的永磁体涡流损耗的有限元计算值和解析计算值分别为761.97和679.15 W，误差为10.87%。与未削极永磁体结构相比，其永磁体涡流损耗下降了36.18%。

综合上述分析，梯形削极永磁体结构的气隙磁密THD比正弦削极永磁体结构的气隙磁密THD高1.04%，正弦削极永磁体结构的电磁转矩比梯形削极永磁体结构的电磁转矩低18.57%，梯形削极永磁体结构的转矩波动比正弦削极永磁体结构的转矩波动高0.88%，梯形削极永磁体结构的永磁体涡流损耗比正弦削极永磁体结构的永磁体涡流损耗高30.07%。正弦削极永磁体结构具有较小的电磁转矩和永磁体涡流损耗的原因是与另外两种结构相比，其永磁体用量最小。梯形削极永磁体结构与正弦削极永磁体结构相比，气隙磁密THD和转矩波动相差不大，而电磁转矩较高。虽然梯形削极永磁体结构的永磁体涡流损耗较高，但是可以通过永磁体分段的方式来进一步减小永磁体涡流损耗，从而缩小与正弦削极永磁体结构之间的差距。同时，正弦削极永磁体的三维结构沿着电机径向呈现半圆台形状，与梯形削极永磁体相比，其加工难度较大。因此，综合考虑气隙磁密THD、电磁转矩、转矩波动、永磁体涡流损耗和永磁体加工难度，最终选择梯形削极永磁体结构。

3.3 分段永磁体涡流损耗分析

为了研究永磁体分段对涡流损耗的影响并确定梯形削极分段永磁体结构的分段数，将永磁体沿径向等长分段。仿真条件为额定工况，其中变频器开关频率为10 kHz。

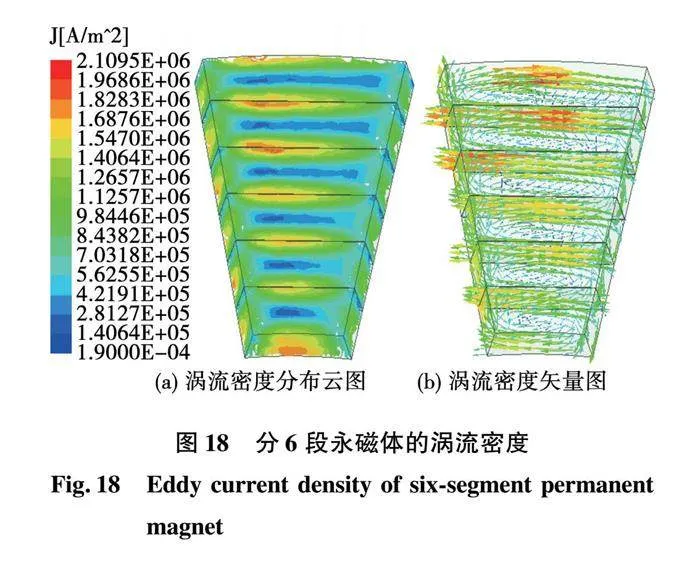
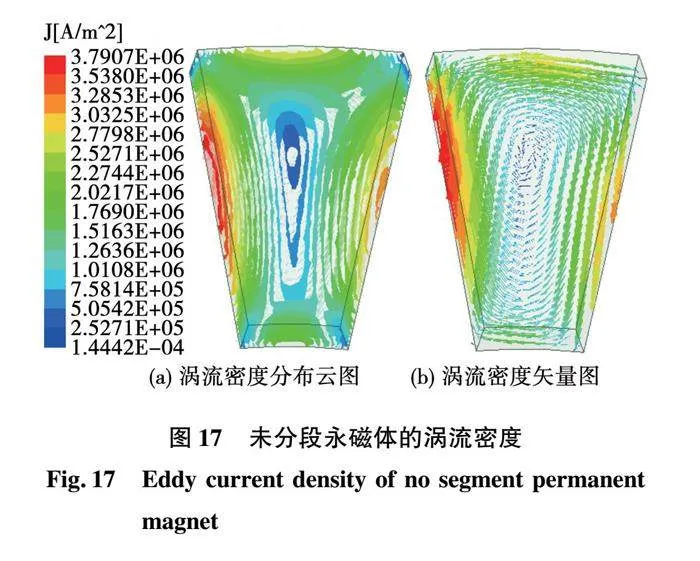
图17和图18分别为永磁体未分段和分成6段的涡流密度分布图。可以看出，永磁体涡流密度分布呈现中间小、四周大、角落小的规律。随着增加永磁体分段数量，涡流路径变得越来越短，涡流密度幅值不断下降，因此永磁体涡流损耗会不断降低。

图19为不同分段永磁体的涡流损耗，与未分段永磁体的涡流损耗相比，分别下降了29.03%、51.20%、65.16%、74.89%、79.77%。若不断增加永磁体的分段数量，虽然永磁体涡流损耗会不断下降，但是工艺难度会不断增加，同时永磁体涡流损耗的下降幅度也会降低。因此，当涡流损耗下降不明显时，分段数量不应继续增加。综合考虑永磁体涡流损耗与工艺难度，最终确定分段数为5段，永磁体涡流损耗为284.51 W。

4 实验验证

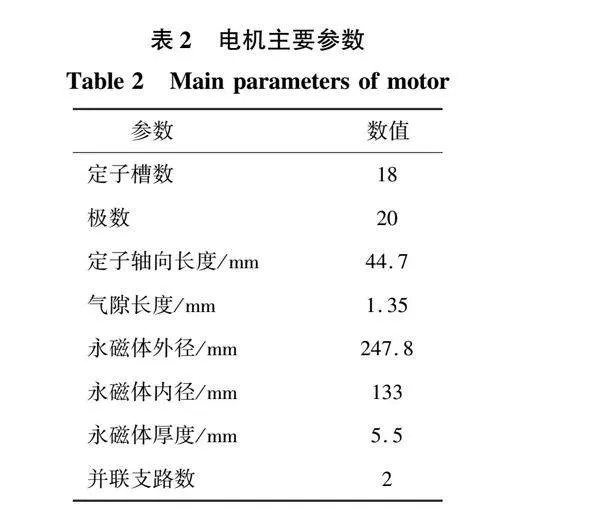
为了验证梯形削极分段结构的计算结果，基于上述结构，研制了一台重量为21 kg的样机，其主要参数如表2所示，样机实物如图20所示。对样机进行实验，实验平台如图21所示。

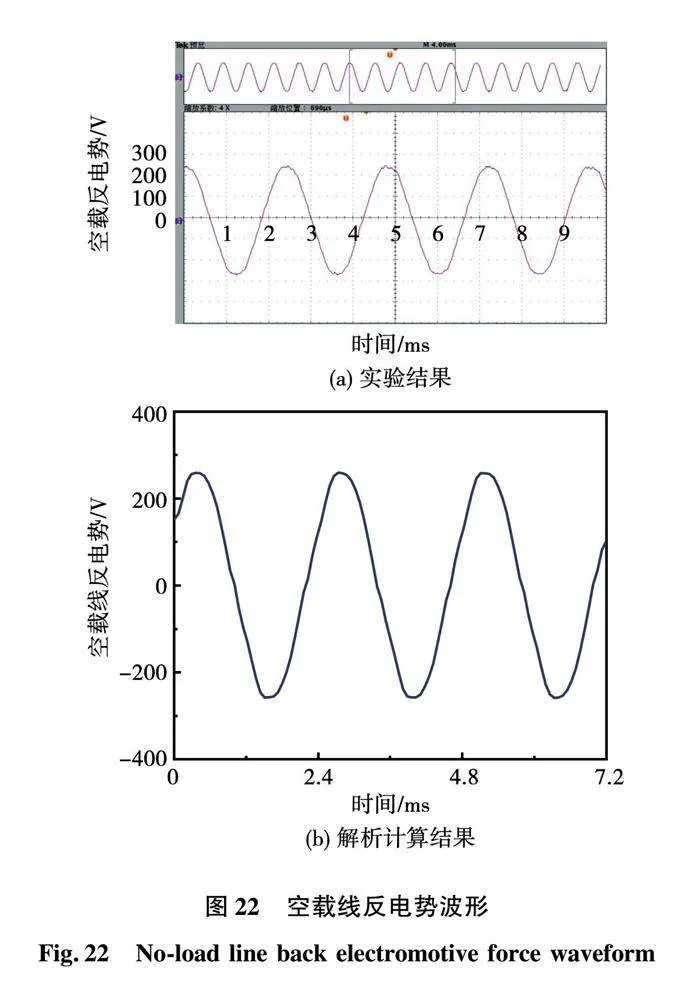
以额定转速2 500 r/min测量样机的线空载反电势，实验结果如图22（a）所示，相同条件下，解析计算结果如图22（b）所示。实验测量线空载反电势为189.8 V，解析计算线空载反电势为183.9 V，计算误差为3.11%，实验结果与计算结果误差较小，结果基本吻合。

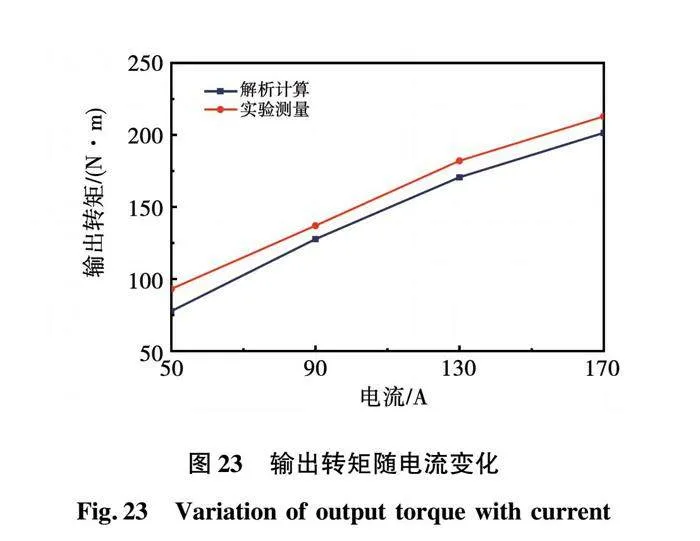
图23为保持电机转速不变时，样机的输出转矩与电流的关系。在额定工况下，实验测量的输出转矩为212.7 N·m，解析计算的输出转矩为201.3 N·m，计算误差为5.36%，实验结果与计算结果误差较小，基本吻合。样机的转矩密度可达10.13 N·m/kg。

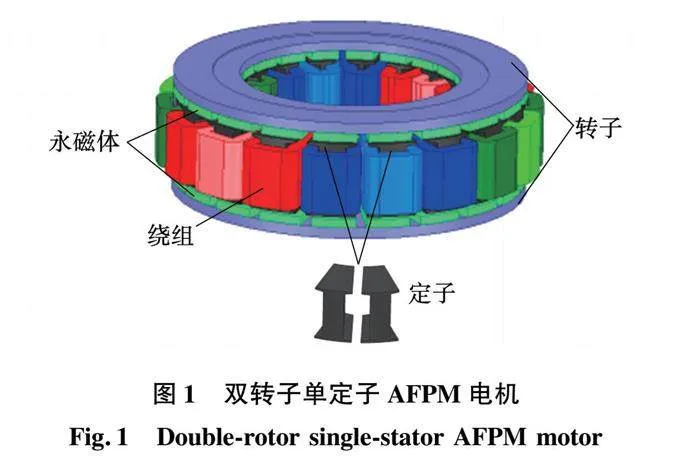
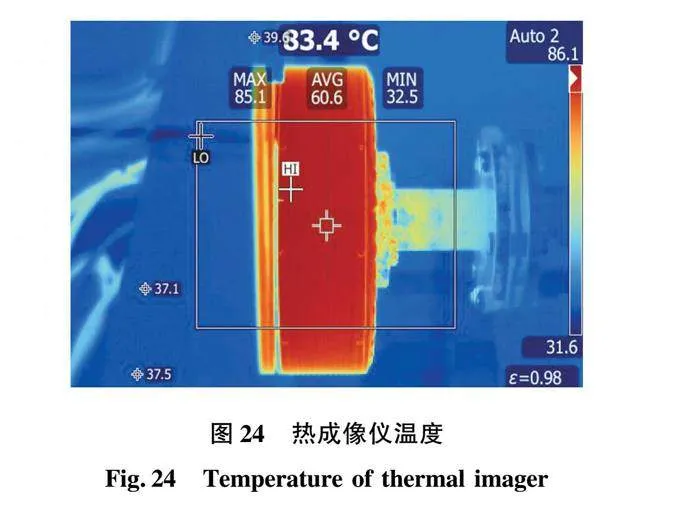
永磁体涡流损耗作为电机的热源，将直接影响电机的温升，因此通过样机温升实验来进一步验证所提结构。样机温升实验的条件为：电机处于额定工况运行、入口水温为25 ℃和入口流量为6 L/min。端盖上预留了观察孔，通过红外线测温仪测量永磁体温度，通过预埋的温度传感器测量绕组温度，采用Fluke-Ti32热成像仪测量外部机壳温度。

图24为外部机壳的热成像仪结果，表3为各部分温度的实验结果与仿真结果，可以看出，实验结果与仿真结果基本吻合。综上所述，通过样机空载实验、负载实验和温升实验验证了梯形削极分段结构可有效降低永磁体涡流损耗并且改善电机输出性能。

5 结 论

本文对表贴式AFPM电机的永磁体结构进行优化，以降低气隙磁密谐波含量并减小永磁体涡流损耗为目标，提出梯形削极分段结构。通过精确子域解析模型和三维有限元对不同永磁体结构的磁场和涡流损耗进行了详细分析。综合考虑负载气隙磁密THD、电磁转矩和转矩波动，确定梯形削极永磁体的削极角度为13°。通过对比不同分段数的梯形削极永磁体涡流损耗和永磁体分段工艺的复杂性，确定永磁体分段数为5段。与本文提到的其他永磁体结构相比，梯形削极分段结构在具有较低的气隙磁密谐波含量和永磁体涡流损耗的同时具有较高的电磁转矩。最终，对一台额定功率为55 kW的样机进行空载实验、负载实验和温升实验，证明了所提结构可有效降低永磁体涡流损耗并且改善电机输出性能。

参 考 文 献：

［1］ 曹君慈， 周柏宇， 李栋， 等. 不同磁极拓扑结构的轴向磁通永磁同步电机传热的研究［J］.电机与控制学报， 2022， 26（5）： 26.

CAO Junci， ZHOU Boyu， LI Dong， et al. Heat transfer of axial flux permanent magnet motor with different magnetic pole topologies［J］. Electric Machines and Control， 2022， 26（5）： 26.

［2］ 李涛， 张幽彤， 梁玉秀， 等. 定子无磁轭模块化轴向磁通永磁电机研究进展综述［J］. 中国电机工程学报， 2021， 41（1）： 340.

LI Tao， ZHANG Youtong， LIANG Yuxiu， et al. An overview on research progress of yokeless and segmented armature axial flux permanent magnet machine［J］. Proceedings of the CSEE， 2021， 41（1）： 340.

［3］ 赵纪龙， 全小伟， 林明耀. 双转子混合励磁轴向磁通切换永磁电机设计与分析［J］. 中国电机工程学报， 2020， 40（24）： 7860.

ZHAO Jilong， QUAN Xiaowei， LIN Mingyao. Design and analysis of a double-rotor hybrid excited axial switched-flux permanent magnet machine［J］.Proceedings of the CSEE，2020，40（24）：7860.

［4］ 耿振， 李光友. 轴向磁通永磁同步电机发展综述［J］. 微特电机， 2015， 43（9）： 88.

GENG Zhen， LI Guangyou. Overview of axial flux permanent-magnet machine ［J］. Small amp; Special Electrical Machines， 2015， 43（9）： 88.

［5］ 佟文明， 马雪健， 位海洋， 等. 基于磁场解析模型与遗传算法的轴向磁通永磁电机多目标优化设计［J］. 电机与控制学报， 2022， 26（1）： 39.

TONG Wenming， MA Xuejian， WEI Haiyang， et al. Multi objective optimization design of axial flux permanent magnet motor based on magnetic field analytical model and genetic algorithm［J］. Electric Machines and Control， 2022， 26（1）： 39.

［6］ 孙明灿， 唐任远， 韩雪岩， 等.高频非晶合金轴向磁通永磁电机不同冷却方案温度场分析［J］. 电机与控制学报， 2018， 22（2）： 1.

SUN Mingcan， TANG Renyuan， HAN Xueyan， et al. Temperature field analysis of a high frequency amorphous alloy axial flux permanent magnet machine with different cooling schemes［J］. Electric Machines and Control， 2018， 22（2）： 1.

［7］ CHENG B， PAN G， MAO Z. Analytical calculation and optimization of the segmented-stator dual-rotor axial flux permanent magnet motors［J］. IEEE Transactions on Magnetics， 2020， 56（11）： 1.

［8］ 王晓远， 齐丹丹， 王辉. 定子无磁轭模块化轴向永磁电机磁极表面开槽分析［J］. 电工技术学报， 2017， 32（16）： 145.

WANG Xiaoyuan， QI Dandan， WANG Hui. Analysis on magnet surface groove of yokeless and segmented armature axial flux motor［J］. Transactions of China Electrotechnical Society， 2017， 32（16）： 145.

［9］ ElHASAN T S， LUK P C K. Magnet topology optimization to reduce harmonics in high-speed axial flux generators［J］. IEEE Transactions on Magnetics， 2003， 39（5）： 3340.

［10］ KANO Y， KOSAKA T， MATSUI N. A simple nonlinear magnetic analysis for axial-flux permanent-magnet machines［J］. IEEE Transactions on Industrial Electronics， 2010， 57（6）： 2124.

［11］ 江善林， 邹继斌， 徐永向， 等. 考虑旋转磁通和趋肤效应的变系数铁耗计算模型［J］. 中国电机工程学报， 2011， 31（3）：104.

JIANG Shanlin， ZOU Jibin， XU Yongxiang， et al. Variable coefficient iron loss calculating model considering rotational flux and skin effect［J］. Proceedings of the CSEE， 2011， 31（3）：104.

［12］ SFAHANI A H， VAEZZADEH S， RAHMAN M A. Performance improvement of permanent magnet machines by modular poles［J］. IET Electric Power Applications， 2009， 3（4）： 343.

［13］ 谢颖， 曲春梅. 梯形永磁体盘式无铁心电机的设计与研究［J］. 电机与控制学报， 2016， 20（8）： 74.

XIE Ying， QU Chunmei. Design and study of disc coreless motor with trapezoidal permanent magnet［J］. Electric Machines and Control， 2016， 20（8）： 74.

［14］ WANG K， ZHU Z Q， OMBACH G. Torque enhancement of surface-mounted permanent magnet machine using third-order harmonic［J］.IEEE Transactions on Magnetics，2014，50（3）： 104.

［15］ CHO H， JANG S. A design approach to reduce rotor losses in high-speed permanent magnet machine for turbo-compressor［J］. IEEE Transactions on Magnetics， 2006， 42（10）： 3521.

［16］ 李雪， 刘福贵， 李博， 等. 轴向磁场无铁心永磁电机的永磁体结构优化及其涡流损耗削弱［J］. 河北工业大学学报， 2019， 48（2）： 33.

LI Xue， LIU Fugui， LI Bo， et al. Optimization of permanent magnet structure and weakening of eddy current loss in axial magnetic field coreless permanent magnet motor［J］. Journal of Hebei University of Technology， 2019， 48（2）： 33.

［17］ HIROAKI T， XIA Z P， WANG J B， et al. Rotor eddy-current loss in permanent magnet brushless machines［J］. IEEE Transactions on Magnetics， 2004， 40（4）： 2104.

［18］ POLINDER H， HOEIJMAKERS M J. Eddy-current losses in the segmented surface-mounted magnets of a PM machine［J］.IEEE Proceeding on Electrical Power Application，1999，146（3）： 261.

（编辑：邱赫男）