一次函数错解“诊疗室”

邹兴平

一次函数是初中数学“数与代数”部分的重要内容，也是中考的必考内容，同学们在初学一次函数相关知识时，经常会因为对概念理解不透、忽视限制条件、考虑问题不全面等原因而出现各种错误．下面就同学们在解一次函数相关问题时经常出现的错误进行剖析，希望大家引以为戒．

一、对一次函数的性质掌握不牢

例1 已知点（-4，y1），（2，y2）都在直线y=-1／2x+2上，则y1，y2的大小关系是（ ）．

A.y1>y2

B.y1=y2

C.y1＜y2

D.不能比较

错解：因为-4<2，所以y1＜y2．故选C．

剖析：上解因没有考虑函数的增减性而出错，由一次函数性质可知：当k>0时，y随x的增大而增大；当k<0时，y随x的增大而减小．因为k=-1/2<0，-4<2，所以y1>y2．

正解：因为k=-1/2<0，所以y随x的增大而减小．因为-4<2，所以．y1>y2.故选A．

二、忽视正比例函数也是一次函数

例2 若一次函数y=kx+b的图象不经过第三象限，则下列结论正确的是（ ）．

A.k<0，b>0

B.k<0，b<0

C.k<0，b≤0

D.k<0，b≥0

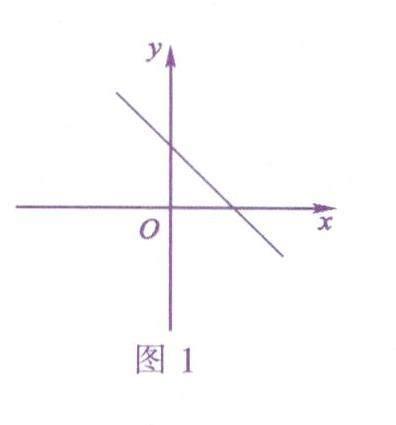
錯解：因为一次函数y=kx+b的图象不经过第三象限，所以函数的大致图象如图1所示．由图象可知k<0，b>0，故选A．

剖析：错解忽视了函数图象可能只经过第二、四象限的情况，正比例函数y=kx是特殊的一次函数，所以当k<0，b=0时，函数图象也不经过第三象限．

正解：选D．

三、忽视分类讨论

例3 已知一次函数y=kx+4的图象与两坐标轴围成的三角形的面积为16，求此一次函数的解析式.

错解：一次函数y=kx+4的图象与y轴和x轴的交点分别是（0，4），（-4/k，0），所以函数图象与坐标轴围成的三角形的面积为1／2×4×（-4／k）=16，解得k=-1/2，所以一次函数的解析式是y=-1/2x+4．

剖析：由于y=kx+4的图象与x轴交点的位置不确定，可能在x轴正半轴上，也可能在x轴负半轴上，所以y=kx+4的图象与坐标轴围成的三角形在x轴上的边长为|-4/k|．应分两种情况进行讨论，否则容易造成漏解．

正解：一次函数y=kx+4的图象与y轴和x轴的交点分别是（0，4），（-4/k，0），所以函数图象与两坐标轴围成的三角形的面积是1/2×4×|-4/k|=16，解得k=±1/2．所以——次函数的解析式是y=1/2x+4或y=-1/2x+4．

四、混淆一次函数图象与直线

例4 已知直线y=mx+2m-4不经过第二象限，则m的取值范围是________．

错解：因为直线y=mx+2m-4不经过第二象限，由一次函数图象的性质可知m>0，2m-4≤0，所以0＜m≤2.

剖析：错解混淆了一次函数图象和直线的区别．当m=0时，y=mx+2m-4=-4.y=-4不是一次函数，但其图象仍是一条平行于x轴的直线，该直线经过第三、四象限，也符合题意．

正解：当m≠0时，直线y=mx+2m-4为一次函数图象．因为图象不经过第二象限，由一次函数图象的性质可知m>0，2m-4≤0，所以0≤m≤2.

五、忽视自变量的实际意义

例5 已知等腰△ABC的周长为20，求底边长y与腰长x之间的函数解析式，并写出自变量x的取值范围．

错解：因为y+2x=20，所以y=-2x+20.

因为腰长为线段长，必须大于0，所以自变量x的取值范围为x>0．

剖析：因为x，y分别为等腰三角形的腰长和底边长，所以必须有x>0，y>0，即-2x+20>0，所以Oy，所以x>5.所以自变量x的取值范围为5

试金石

1.若对于每个x，y是y1=2x，y2=x+2，y3=13/2x+12三个值中的最大值，则当x变化时，y的最小值为（ ）．

A.4 B.6

c.8 D.48/7

2.已知一次函数y=2x+m的图象不经过第二象限，则，m的取值范围是________．

3.已知一次函数的图象经过（0，-2），且与两坐标轴围成的三角形的面积为3．求一次函数的解析式．

（参考答案在本期找）