紧抓特征 触类旁通

陈源

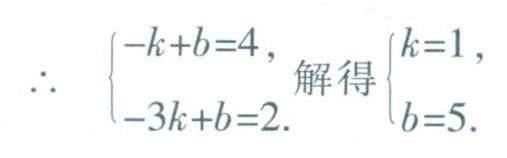
描述函数关系的方法有很多，常见的有列表法、解析式法和图象法．对于一次函数，新课标指出，要结合具体情境体会一次函数的意义，能根据已知条件确定一次函数的解析式．下面结合典型例题，谈谈确定一次函数解析式的几类常见题型．

一、定义型

例1 已知y=（m2-2m+3）x2|m|-1-5是关于x的一次函数，求该函数的解析式，

解：∵y=（m2-2m+3）x2|m|-1-5是关于x的一次函数，

∴2|m|-1=1.

解得，n=±1．

当m=1时，m2-2m+3=2；

当m=-1时，m2-2m+3=6.

∴该函数解析式为y=2x-5或y=6x-5．

二、一点型

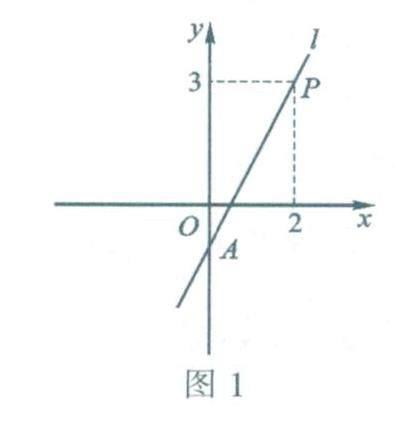
例2 如图1，已知直线l：y=kx-1经过点A与点P（2，3）.

（l）求直线l的解析式．

（2）若在y轴上有一点B，使△APB的面积为5，求点B的坐标．

解：（1）把P（2，3）代人y=kx-1，得3=2k-1，解得k=2．

所以直线l的解析式为y=2x-1．

（2）设点B的坐标为（0，t）.

当x=0时，y=2x-1=-1，则A（0，-1）．

∴S△APB=1/2×|t+1|×2=5．

解得t=4或t=-6.

∴点B的坐标为（0，4）或（0，-6）．

三、两点型

例3 在平面直角坐标系内有三点：A（-1，4），B（-3，2），C（0，6）.

（1）求过其中两点的直线的解析式（选一种情形作答）．

（2）判断A，B，C三点是否在同一直线上，并说明理由．

解：（1）设A（-1，4），B（-3，2）两点所在直线的解析式为y=kx+b.

∴直线AB的解析式是y=x+5．

（2）当x=0时，y=0+5≠6．

∴点C（0，6）不在直线AB上，即A，B，C三點不在同一条直线上．

五、图象型

此时直线BC的解析式为y=3x+6.

综上，直线BC的解析式为y=-3x+6或y=3x+6．

六、平移型

例6 已知一次函数y=x+2．将该函数的图象向下平移m个单位长度得到直线2，且直线l经过点C（2，-3）．求直线l对应的函数解析式．

解：由题意可知，直线f的函数解析式为y=x+2-m.

∵直线f经过点C（2，-3），

∴-3=2+2-m.解得m=7．

∴直线l对应的函数解析式为y=x-5．

确定一次函数解析式的题型丰富多样．在不同的问题情境中，只要我们善于发现题目特征，捕捉关键信息，就能迅速找到合适的解法，得出正确的答案．