“数据的分析”新题总动员

陈德前

一、选择题

1.（湘潭）某校组织青年教师教学竞赛活动，包含教学设计和现场展示两个方面．其中教学设计占20%，现场展示占80%.某参赛教师的教学设计的得分为90分，现场展示的得分为95分，则她的最后得分为（ ）．

A.95分 B.94分 C.92.5分 D.91分

2.（龙东）一组数据1，0，-3，5，x，2，-3的平均数是1，则这组数据的众数是（ ）．

A.-3 B.5

C.-3和5 D.1和3

3.（牡丹江）一组数据1，x，5，7有唯一众数，且中位数是6，则这组数据的平均数是（ ）．

A.6 B.5 C.4 D.3

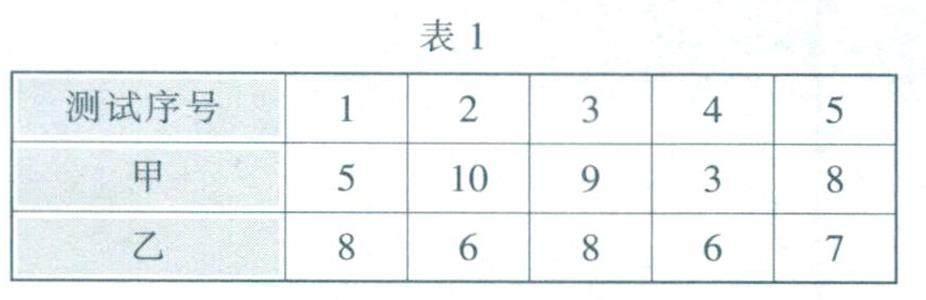
4.（衡阳）某射击运动队进行了五次射击测试，甲、乙两名选手的测试成绩如表1所示．甲、乙两名选手成绩的方差分别记为s2甲和s2乙，则s2甲和s2乙的大小关系是（ ）.

A.s2甲>s2乙 B.s2甲＜s2乙

C.s2甲=s2乙 D.无法确定

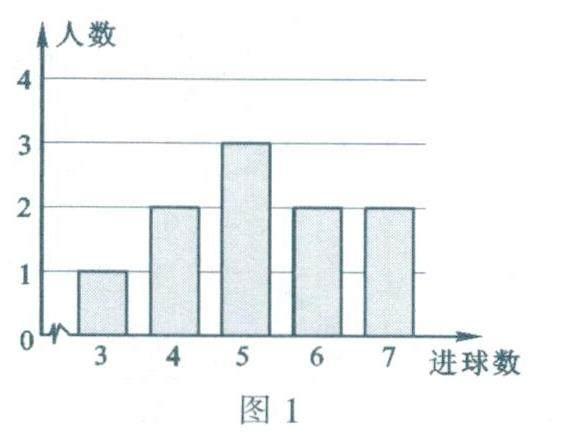
5.（济宁）为检测学生体育锻炼效果，从某班随机抽取10名学生进行篮球定时定点投篮检测，统计进球数如图1所示．对于这10名学生的定时定点投篮的进球数，下列说法中错误的是（ ）．

A.中位数是5 B.众数是5

C.平均数是5.2 D.方差是2

二、填空题

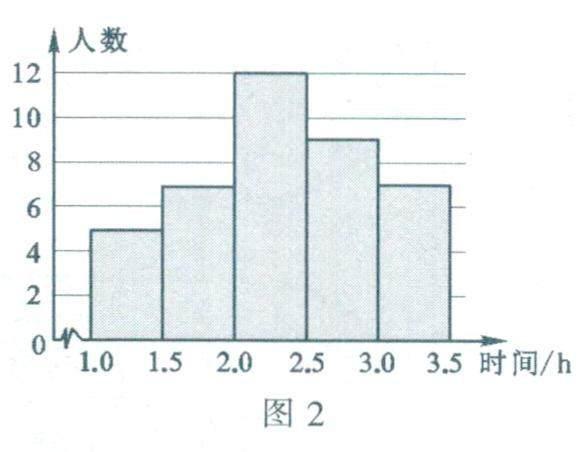
6.（泰州）七（1）班40名同学上周家务劳动时间的频数分布直方图如图2所示，设这组数据的中位数为m．则m________2.6（填“>”或“=”或“<”）．

7.（福建）某公司对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达三方面的测试，他们的各项成绩（百分制）如表2所示．如果将每位应聘者的综合知识、工作经验、语言表达的成绩按5：2：3的比例计算出总成绩，并录用总成绩（百分制）最高的应聘者，则被录用的是________．

8.（德阳）在一次数学测试中，张老师发现一小组6名学生的成绩（单位：分）分别为85，78，90，72，●，75，其中有一名学生的成绩被墨水污染．已知该小组的平均成绩为80分，则该小组成绩的中位数是________．

三、解答题

9.（河南）蓬勃发展的快递业，为全国各地的新鲜水果及时走进千家万户提供了极大便利．不同的快递公司在配送、服务等方面各具优势．樱桃种植户小丽经过初步了解，打算从甲、乙兩家快递公司中选择一家合作．为此，小丽收集了10家樱桃种植户对两家公司的相关评价，并整理分析如下．

a.配送速度得分（满分10分）：

甲：6 6 7 7 7 8 9 9 9 10

乙：6 7 7 8 8 8 8 9 9 10

b.服务质量得分统计图（图3）（满分10分）：

c.配送速度和服务质量得分统计表：

根据以上信息，回答下列问题：

（1）表格中的m=________，s2甲________s2乙（填“>”或“=”或“<”）．

（2）综合上表中的统计量，你认为小丽应选择哪家公司？请说明理由．

10.（安徽）在端午节来临之际，某校七、八年级开展了一次“包粽子”实践活动．对学生的活动情况按10分制进行评分，成绩（单位：分）均为不低于6的整数．为了解这次活动的效果，现从这两个年级中各随机抽取10名学生的活动成绩作为样本进行整理，并绘制统计图表（表4和图4）．部分信息如下．

已知八年级10名学生活动成绩的中位数为8.5．

请根据以上信息，完成下列问题．

（1）在样本中，七年级活动成绩为7分的学生人数是________，七年级活动成绩的众数为________．

（2）a=________，b=________．

（3）若认定活动成绩不低于9分为“优秀”，根据样本数据，判断本次活动中优秀率高的年级是否平均成绩也高，并说明理由．

（参考答案在本期找）