例谈不等式恒成立求参数范围问题的解题策略
2024-05-20湖南省永州市第一中学周建权
⦿ 湖南省永州市第一中学 周建权
不等式恒成立求参数范围的问题能够充分联系不等式、函数与方程、导数等知识,有利于考查学生数学运算、逻辑推理、数学抽象等学科核心素养,是高考和各地模考的热点问题.此类问题形式多变、综合性强,学生往往捉摸不透,本文中结合具体例子谈谈此类问题的解题策略.
1 分离参数法
分离参数法就是对不等式变形,将参数与变量分离,构造无参数函数,进而研究该函数的最值.

下面重点研究第(2)问的解题策略.

当x=0时,不等式为1≥1,显然成立,符合题意.
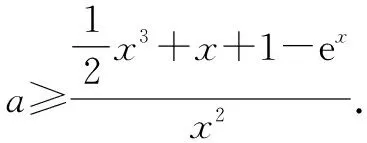

对g(x)求导,得
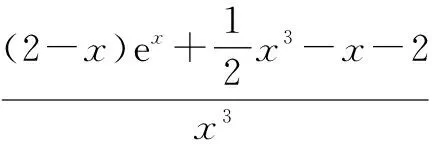

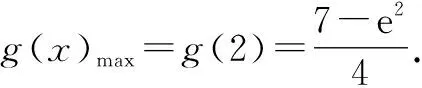
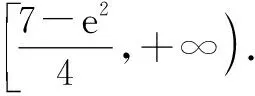

2 不分离参数,构造函数
参变不易分离,或分离后函数结构复杂不易研究,则可不分离参数,将参数和变量放到不等式同一侧,直接构造含参函数.
2.1 直接分析最值
下面给出例1的解法2.
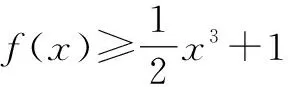
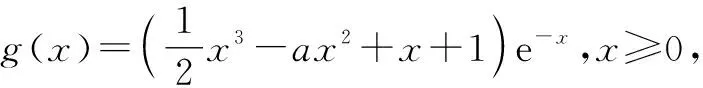
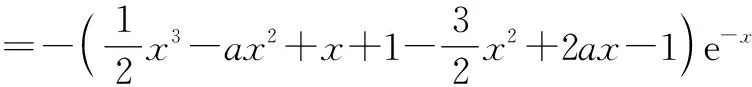
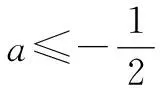

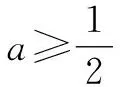
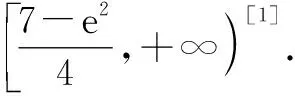
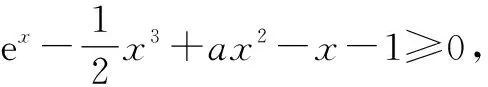
2.2 必要性探路法
必要性探路法指的是利用不等式在一些特殊情况下成立,得到参数的一个取值范围,该范围是不等式恒成立的一个必要条件,如果能证明该范围也是不等成立的充分条件,则该范围即为所求,如果不是充分条件,也缩小了参数的范围.
(1)端点效应探路
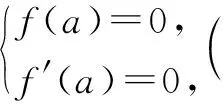
例2(2022年新高考Ⅱ卷第22题)已知函数f(x)=xeax-ex.(1)略.(2)当x>0时,f(x)<-1,求a的取值范围.
解:设h(x)=xeax-ex+1,则当x>0时,恒有h(x)<0.
注意到h′(x)=(1+ax)eax-ex,所以h′(0)=0.
设g(x)=(1+ax)eax-ex(x>0),则g(0)=0,且
g′(x)=(2a+a2x)eax-ex.

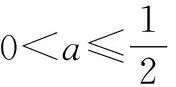
h′(x)=(1+ax)eax-ex=eax+ln (1+ax)-ex.
下证:对任意x>0,总有ln(1+x) 故x>0时S(x) eax+ln (1+ax)-ex 所以h′(x)≤0总成立,则h(x)在(0,+∞)上为减函数,故h(x) 当a≤0时,有h′(x)=eax-ex+axeax<1-1+0=0,所以h(x)在(0,+∞)上为减函数,故h(x) 评析:含参函数求最值时往往需要对参数进行分类讨论,分类标准的确定是难点和关键点.如本题仅从h′(x)=(1+ax)eax-ex的形式较难发现对a进行讨论的分类点,如果用端点效应来看,思路就比较清晰了.实际上,利用端点效应有助于确定参数分类讨论的标准. (2)其他特殊点探路 例3(2020年新高考Ⅰ卷第21题)已知函数f(x)=aex-1-lnx+lna.(1)略.(2)若不等式f(x)≥1恒成立,求a的取值范围. 解法1:因为f(x)≥1恒成立,所以f(1)=a+lna≥1.令g(a)=a+lna,则g(a)在(0,+∞)单调递增,且g(1)=1,故由g(a)≥1,得a≥1. 下面证明a≥1时,f(x)≥1恒成立. 当a≥1时,f(x)=aex-1-lnx+lna≥ex-1-lnx. 综上所述,a的取值范围是[1,+∞). 评析:利用端点、定点、极点等特殊点探路,需要对不等式结构有较强的观察分析能力,需要有函数意识、数形结合意识.通过必要性探路,能够化繁为简,理清讨论的思路,同时也要注意,有时我们找到的必要条件不一定刚好也是充分条件. 分离函数法,就是对不等式恒等变形,将一个复杂的含参不等式分解成不等号左右两边各一个函数的形式,进而研究这两个函数的关系. 下面给出例3的解法2. 解法2:由f(x)≥1,得aex-1-lnx+lna≥1,即eln a+x-1+lna+x-1≥lnx+x,而lnx+x=eln x+ lnx,所以eln a+x-1+lna+x-1≥eln x+lnx. 令h(m)=em+m,则有h(lna+x-1)≥h(lnx). 因为h′(m)=em+1>0,所以h(m)在R上单调递增,于是可得lna+x-1≥lnx,因此只需lna≥(lnx-x+1)max. 因此a的取值范围为[1,+∞). 评析:同构指的是结构或形式相同,一些不等式可以通过变形使不等式两侧呈现相同结构,将该结构抽象出来构造函数,利用所构造函数的单调性将结构复杂的恒成立问题转化为结构简单的恒成立问题.同构法在“指对混合不等式”出现时用得较多,对代数变形能力要求较高,体现了数学的和谐对称美,对培养数学抽象、数学运算等核心素养具有重要意义. 图1 评析:数形结合法就是通过分离函数,将问题转化为两个函数图象位置关系的问题.分离出来的两个函数一般是“一直一曲”,便于研究位置关系.分离函数后正确画出函数的图象是解题的关键,需分析函数的定义域、值域、单调性、对称性、凹凸性、特殊点等. 对于不等式恒成立求参数范围的问题,从参变分离的程度来看,若参变完全分离,则构造的是无参数函数,能够避免对参数的讨论,但存在无参函数结构复杂,不易研究的情况;若参变不分离,则构造的是含参函数,对参数讨论标准的确定是难点所在,需对常见超越函数的性质有所积累,有时必要性探路法能提供思路;若参变部分分离,即分离函数法,有时能够巧妙避免函数结构复杂的情况和对参数的讨论,要明确分离的目标往往是构造同构式或便于数形结合的函数.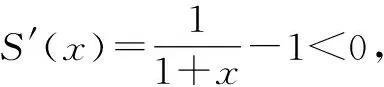

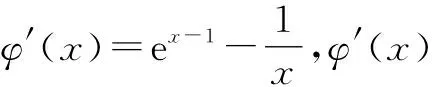
3 分离函数法
3.1 构造同构式

3.2 数形结合

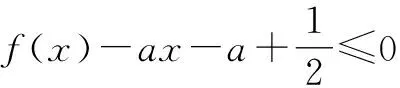
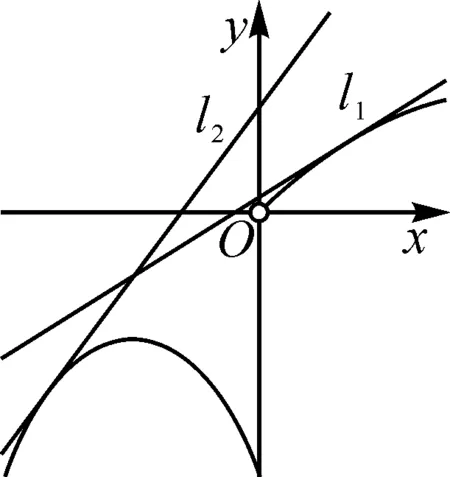
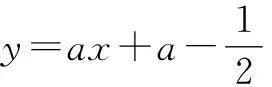
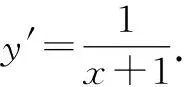
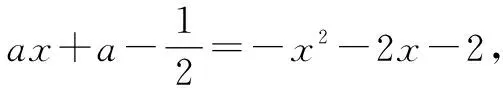
4 解题感悟
