切点弦场景创设,定点与动点轨迹——一道抛物线题的探究

⦿ 江苏省苏州工业园区星海实验高级中学 卢 闯

切点弦是二次曲线中一类比较特殊的弦,其是由二次曲线外的一点向二次曲线引两条切线,连接两切点的线段.特别对于抛物线中的切点弦问题,更是其中一个具有独特属性的知识点,备受关注.

1 问题呈现

问题(2024届广东四校高三第一次联考数学试卷·16)过P(m,-2)向抛物线x2=4y引两条切线PQ,PR,切点分别为Q,R.又点A(0,4)在直线QR上的射影为H,则焦点F与H连线的斜率的取值范围是______.

2 问题剖析

此题以过定直线中的动点向抛物线引两条切线来设置问题场景,结合抛物线切点弦的构建,以及定点到切点弦上的射影的给出,确定焦点到对应射影的连线的斜率问题,以直线斜率的取值范围来构建问题.

本题涉及动点、切点、定点、射影、焦点等众多类型的点,切线、弦点弦、焦点与射影的连线等对应类型的直线,创设一个“动”“静”结合的和谐场景,以定直线上动点的变化带动切线的变化,引起切点弦的变化,进一步带动定点在切点弦上的射影的变化,最后直接关系到焦点与射影连线的斜率的变化,“定值”与“变量”的巧妙转化,构建一个动态情景,同时也为问题的解决提供切入点.

本题可以从众多类型的点入手加以设点法处理,也可以从众多类型的直线入手加以设线法处理,都可以很好达到解决问题的目的.若理解并掌握圆锥曲线切点弦公式的话,可直接利用“二级结论”快捷处理.

而对于该问题,当动点P(m,-2)中m=0时,焦点F与点H的连线是一条怎样的直线,是否存在斜率呢?这也是该问题命制过程中的一个弊端所在,要加以合理的修正与改进,以保证命题的完善性.

3 问题破解

方法1：设点法——导数思维.

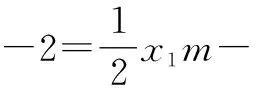
用x2替换x1,用y2替换y1,可知点R也是直线mx-2y+4=0上的点.所以直线QR的方程为mx-2y+4=0.

将上述方程变形,得mx=2(y-2),从而直线QR过定点B(0,2).

而由于AH⊥BH,|AB|=2,则知点A在直线QR上的射影H的轨迹就是以AB为直径的圆,其方程为x2+(y-3)2=1.

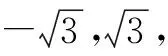
图1

解后反思：通过设点法,结合导数的几何意义来确定圆锥曲线的切线方程,为进一步求解圆锥曲线的切点弦提供条件.这是圆锥曲线的切点弦方程求解的一种“通性通法”.而基于抛物线的切点弦方程,通过对直线过定点的挖掘,以及射影轨迹的判断,为数形结合确定对应直线斜率的极端情况打下基础.同时要注意直线斜率的取值范围以及图形之间的联系,不要出现混淆.

方法2：设线法——方程思维.

解析：设切线PQ,PR的方程分别为

y=k1(x-m)-2,y=k2(x-m)-2.

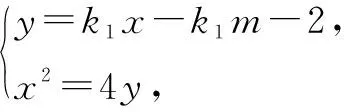
于是可知k1,k2是方程k2-km-2=0的两个根,利用韦达定理可得k1+k2=m,k1k2=-2.

解后反思：通过设线法,结合方程的判别式来确定圆锥曲线的切点弦所在的直线方程,为进一步求解圆锥曲线的切点弦提供条件.这是圆锥曲线的切点弦方程求解的另一种“通性通法”.思维视角不同,对数学基础知识的理解与应用也有所侧重,关键是把握问题的内涵与实质,巧妙加以综合与应用.

方法3：性质法.

4 问题辨析

在以上问题中,对于动点P(m,-2),若m=0时,此时点P(0,-2),过点P向抛物线x2=4y引两条切线PQ,PR,利用抛物线的对称性可知,切点Q,R关于y轴对称,由此可得点A(0,4)在直线QR上的射影H在y轴上,而焦点F(0,1)也在y轴上,可知FH的方程为x=0,此时,FH的斜率不存在.

由以上问题的特殊场景分析可知,在原问题的设置中,应该把m=0这一特殊情况排除在外,由此对原问题进一步加以改进如下：

问题过P(m,-2)(m≠0)向抛物线x2=4y引两条切线PQ,PR,切点分别为Q,R.又点A(0,4)在直线QR上的射影为H,则焦点F与H连线的斜率的取值范围是______.

这样修改后,问题更加合理与完善,不存在漏洞或不合理的地方,而具体的解析过程也更加合理有效.

5 变式拓展

借助原问题解析过程中的产物,可以得到一些相应的变式问题.

5.1 定点问题

变式1过P(m,-2)向抛物线x2=4y引两条切线PQ,PR,切点分别为Q,R,则直线QR恒过的定点的坐标是______.(答案：(0,2).)

由此可得更加一般性的结论：

结论：过P(m,a)(a<0)向抛物线x2=2py(p>0)引两条切线PQ,PR,切点分别为Q,R,则直线QR恒过的定点的坐标是(0,-a).

5.2 轨迹问题

变式2过P(m,-2)向抛物线x2=4y引两条切线PQ,PR,切点分别为Q,R.又点A(0,4)在直线QR上的射影为H,则动点H的轨迹方程是______.(答案：x2+(y-3)2=1.)

6 教学启示

二次曲线(圆、椭圆、双曲线与抛物线)中的切点弦问题,是平面解析几何中一类综合性较强的问题,解决这类问题的“通性道法”主要有两种：(1)结合函数与导数的应用,利用导数的几何意义确定对应的切线方程,进而加以深入综合与应用;(2)结合函数与方程的应用,利用方程的判别式确定对应的切线方程,同时为切点弦的确定提供条件.

而特殊的思维技巧就是借助二次曲线的切点弦方程的“二级结论”,直接利用公式确定切点弦方程,快速解决问题.

常规的技巧方法是我们必须理解并掌握的知识,也是对此类问题的基本要求,需要借助知识的学习与练习的训练加以掌握与应用;而特殊的思维技巧给我们的课外学习开辟了一个更加宽广的空间,提供了更加简单快捷的技巧与方法.