“三叉戟”模型在解析几何中的深度应用

⦿ 河北定州中学 陈淑红

⦿ 北京交通大学 朱奕帆

平移齐次法是近几年网上非常流行的解决圆锥曲线综合问题的方法.处理方法是先平移坐标系,将给定的点平移至坐标原点,转化为两直线过原点的类型,齐次化后两直线的斜率之和(或积)为常数,可以解决与斜率之和(或积)有关的定点、定值或轨迹等问题.过定点的两条直线与圆锥曲线有两个交点,定点和两个交点构成三角形,由于三角形形状类似三叉戟,因此我们把这种模型称为“三叉戟”模型.

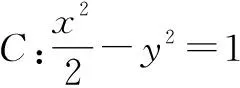
分析：△APQ由定点A和两个交点P,Q构成,符合“三叉戟”模型,可以采用平移齐次法,将双曲线向左平移2个单位长度,向下平移1个单位长度,消去常数项,与PQ平移后的直线P′Q′联立,运用韦达定理得到直线OP′,OQ′的斜率之和为0.

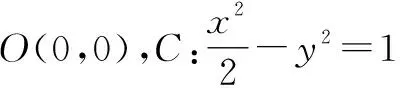
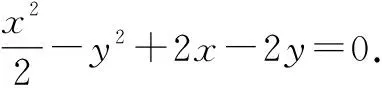
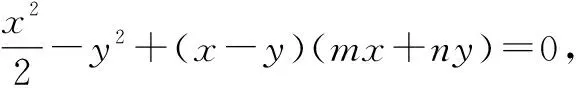
上式两边同除以x2,得

因为平移前后两直线的斜率不会发生改变,所以直线l的斜率为-1.

(1)当l与x轴垂直时,求直线AM的方程;

(2)设O为坐标原点,证明：∠OMA=∠OMB.

分析：本题第(2)问实质是要证明kOA+kOB=0,应用“三叉戟”模型,利用韦达定理表示斜率的和与积,但是因为点M不在椭圆上,平移后椭圆的方程中既包含x,y的二次项和x,y的一次项,还包含常数项,对运算求解能力提出了更高的要求.

解：(1)解答略.

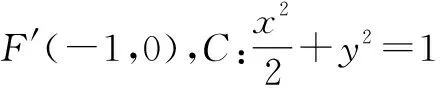
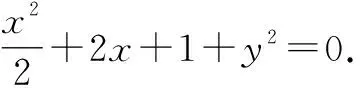
将直线AB平移至A′B′：x=my-1,即1=my-x.

将C′的方程齐次化,得

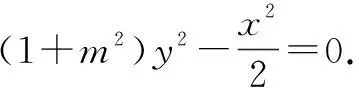
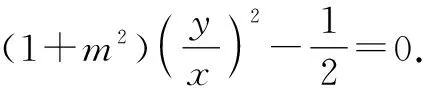
所以kO′A′+kO′B′=0,即∠OMA=∠OMB.

将直线方程以“1”的形式代入圆锥曲线,可以直接乘在一次式上,也可以平方后乘在常数项上,凑成齐次式.

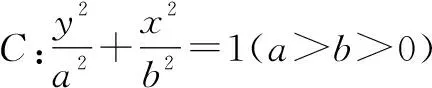
(1)求椭圆C的方程;

(2)过点B(-2,3)的直线交椭圆于P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明：线段MN的中点为定点．

分析：平移坐标系后,线段MN的中点为定点等价于直线OP′,OQ′与x=2交点的中点为定点.

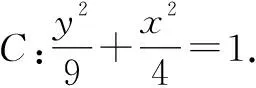
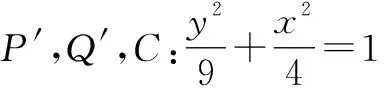
由题意知,直线P′Q′的斜率存在.

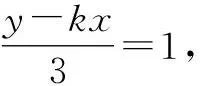
设OP′：y=k1x,OQ′：y=k2x,分别与x=2联立得到yM′=2k1,yN′=2k2.

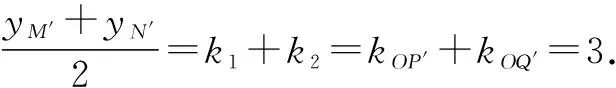
因为平移前后中点的位置相对不变,所以线段MN的中点为定点(0,3).

分析：按传统方法求解,直线PA,PB与直线CD的交点坐标计算量大,平移后,转化为过原点的两条直线与另一条直线的交点,交点坐标均用斜率来表示.

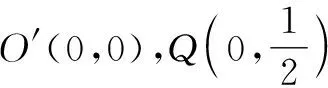
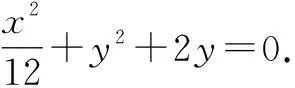
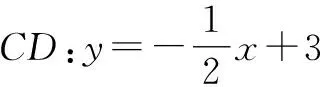
令kO′A′=k1,kO′B′=k2,则

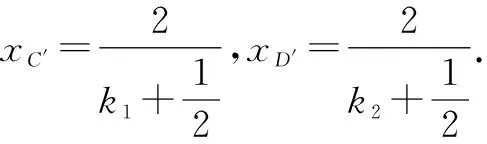
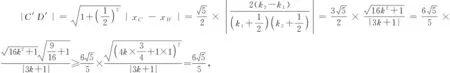
对于圆锥曲线中的双斜率问题,常规方法是联立方程,结合韦达定理求解,若题目中出现了过定点的“三叉戟”模型,可以选择平移齐次法减少运算.平移齐次法的本质是用过原点的两条直线的斜率表示相关元素,符合解方程组联立代入的思想,是解析几何运算思路的拓展和引申.