借助高质量提问 打造高品质课堂*

⦿ 江苏省东台市安丰中学 丁华干

课堂是师生互动交流的平台,课堂教学离不开师生的对话.若课堂上没有对话,课堂教学就成了教师的独角戏,这样势必会影响学生参与课堂的积极性,影响课堂教学效果.在日常教学中,教师应为学生提供一个平等对话的教学环境,通过对话了解学生所思、所想,以此提高学生参与课堂的积极性,提高教学效率.课堂提问是师生进行互动交流的主要途径.课堂上,教师既要结合教学实际提出有效的问题,也要提供机会让学生提问,以此让学生在问题的引领下更好地理解知识、应用知识,提升教学品质[1].不过,在实际教学中,部分教师常常是为了提问而提问,表面上调动了学生参与课堂的积极性,然却并未引发深度思考,从而使课堂提问失效.教师在设计问题时应认真研究学生,基于学生的最近发展区提出高质量的问题.另外,在实际教学中,教师不能因为追求效率而剥夺学生的话语权,否则课堂提问就会流于形式,容易挫伤学生的积极性.那么,在课堂教学中,如何通过有效的课堂提问来提升课堂教学效率呢?笔者结合教学实际谈几点心得体会,供参考!

1 课前提问恰到好处,激发学生的探究欲

在新知教学中,大多教师会采用课前提问的方式来吸引学生的注意力.课前提问的方式是多种多样的,如情境式、类比式、开门见山式、回顾概念式等.不同的提问方式有着不同的作用,教师要结合教学实际合理选择,以此通过恰到好处的提问来激发学生的探究欲,提高教学效率.

案例1“椭圆标准方程”教学片段.

师：谁来说一说,圆的定义是什么?它的标准方程又是什么呢?

问题给出后,教师点名让基础较为薄弱的学生回答,学生顺利地给出了正确答案.

师：看来大家对圆的定义及其标准方程已经了如指掌了.若圆的圆心为原点,那么圆的标准方程是什么呢?

生1：x2+y2=r2.

师：你能把它变得更简洁一点吗?(生沉思)

师：这和我们之前学过的哪种直线方程类似?

师：很好!此时在x轴和y轴上的截距分别是多少呢?

生3：在x轴和y轴上的截距是±r.

师：非常好.谁来说一说,椭圆的定义是什么?

同样,教师点名让学生陈述椭圆的定义.

师：椭圆也是一种很美的图形.类比研究圆的过程,现在我们需要先研究什么呢?

生齐声答：椭圆的标准方程.

在引入环节,为了吸引学生的注意力,提升思维的连贯性,教师在课堂提问时从学生已有经验出发,引导学生进行新旧知识对比,展现了数学知识的简洁美和统一美,激发了学生的探究欲.同时,教师引导学生与圆的学习过程相类比,为新知的探究架桥铺路,为椭圆标准方程的化简埋下伏笔.

课前提问不是简单的旧知回顾,也不是花里胡哨的摆设,而是诱发学生思考、激发学生探究热情的导火索.教学中,教师要认真研究教学内容,通过创设有针对性的问题来激发学生探索新知的热情,以此将思维引向深处,提高课堂教学有效性[2].

2 重视揭示问题本质,诱发学生深度思考

数学课堂离不开解题,解题是巩固知识、强化技能的重要手段.在讲题的过程中,教师要改变“填鸭式”的讲授,应重视挖掘题目背后的价值,通过课堂提问帮助学生理解问题的本质,掌握解决一类问题的方法,培养思维的深刻性,提高学生举一反三的能力.

案例2已知等差数列{an}的前n项和是Sn,且S10=100,S100=10,则S110=______.

案例2为基础题,大多学生根据等差数列的求和公式,通过列方程组易于求得S110=-110.若在讲解过程中,仅追求结果未免会让学生感觉枯燥乏味,难以发挥典型例习题的价值,学生收获甚微.为了让学生领悟问题的本质,教师做了如下引导：

师：大家都知道数列是特殊的函数,对于案例2,你感受到它的“函数味”了吗?

问题给出后,学生积极思考,尝试从函数的角度思考问题.

生1：Sn是n的二次函数,可设Sn=An2+Bn,根据待定系数法列方程组

由此可以求出Sn的表达式,继而求出S110.

师：很好.那么除了可以将其看成特殊的二次函数,是否还可以看成其他函数呢?

师：很好,这样将问题转化为已知直线上两点,求第三点的问题,其解题过程更方便.

在解题过程中,教师要引导学生从不同的角度审视问题,充分暴露学生审题和解题的思维过程.这样不仅可以提高学生参与课堂的积极性,而且可以发散学生的思维,帮助学生积累丰富的解题经验,有助于学生认知结构的优化和解题能力的提升.

在数学教学过程中,教师应重视挖掘例习题的潜在功能,通过有效的提问引发学生深度思考,以此通过思维的深度对话来激发学生潜能,提高学生数学学习的积极性.

3 合理应用课堂生成,提升课堂对话品质

学生是课堂的主体,在课堂互动中会产生许多生成性资源.在实际教学中,部分教师为了完成教学计划,常常对一些课堂生成置之不理,从而严重挫伤学生学习的自信心,影响教学效果.要知道,课堂是动态变化的,这些课堂生成是学生思维活动的真实反馈,若在教学中合理利用往往可以达到激发学生学习兴趣,诱发学生深度思考的效果.因此,在日常教学中,教师要及时捕捉这些课堂生成,并结合课堂生成不断调整教学活动,以此提升教学品质.

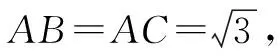
案例3为某次模拟考试填空题的压轴题,问题给出后,教师让学生独立思考,并展示学生的思维过程.

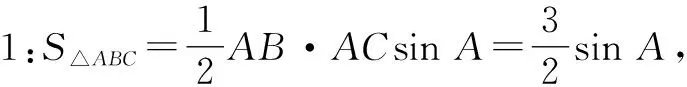
生1的解题过程给出后,很多学生认为该题作为压轴题不可能这么简单.另外,“PB2+PC2=3PA2=3”这个条件并没有用到,所以学生认为该解法是错误的,但是一时却不知道问题出现在哪里.

师：谁知道生1问题出在哪里?

生1：应该是sinA的范围错了?

师：sinA≤1不对吗?(生陷入沉思)

生2：不妨先建系.若∠A=90°,设P(x,y),根据条件PB2+PC2=3PA2=3建立方程组,该方程组无解,所以∠A≠90°.

师：那么sinA的范围是什么呢?(生认真思考)

师：根据已知,若直接求解可能存在一定困难,是否可以考虑“曲线救国”呢?

生3：由条件PB2+PC2=3,联想到cosA.由sin2A=1-cos2A,结合余弦定理,可以将问题可以转化为“当BC取何值时,△ABC面积取最大值?”

师：很好,转化后就绕开了研究角的取值范围这个难点.对于BC,你有什么想法吗?

生4：建系,将PB2+PC2=3PA2=3转化为两圆有公共点,这样即可求出BC的范围.

以上解法并不在教师的预设范围内,但是该课堂生成具有研究价值,为此教师在此基础上顺势引导,得到了新的解题方法,促进了学生分析和解决问题能力的提升.

课堂是师生共同学习、共同建构的平台.在解题过程中,教师不能硬邦邦地将自己的思路讲授给学生,也不能硬生生地将学生的思路拉回至预设的解法上来,而要客观地、科学地对待课堂生成,学会用学生的思维思考问题.教学中,教师需要改变传统的“生拉硬拽”,善于通过启发和引导让学生知道问题出现在哪里,如何找到正确的解决方法,以此通过引导性的提问将学生的思维一步步引入问题的核心,这样不仅有利于问题的解决,而且有利于学生综合能力的提升.总之,教师作为课堂对话的主导者,要认真研究教学、研究学生、研究教材,不断更新教学观念,提升教学技能,通过高质量的提问来诱发学生的深度思考,让师生在深度对话中都能有所成长,有效提升课堂教学质量.