改进分散搜索算法求解包装废弃物回收路径规划问题

张琦琪，陈群

改进分散搜索算法求解包装废弃物回收路径规划问题

张琦琪，陈群*

（上海出版印刷高等专科学校，上海 200093）

将包装废弃物回收路径规划归纳为一个带回路和时间窗的逆向物流车辆路径问题（RL-VRPBTW），以最小化回收成本、发车成本和时间窗惩罚为联合优化目标进行建模。引入“车辆剩余空间回收能力”因素，改进经典节约里程算法，求得较好的初始解；基于分散搜索框架，设计基于初始解改进的分散搜索算法（ISISS），根据问题模型，采用含0的编码方式，通过多样性产生、参考集更新、子集产生、子集合并、解改进等5个步骤实现算法功能。在“部分回收点分布较密集”的城市型地理场景下，针对快消企业的低值固废包装，生成回收点数量分别为50、100、200的3种规模算例，并考虑大小两种车型进行仿真实验。将ISISS算法与改进节约里程、遗传和分散搜索3种算法比较后可知，ISISS算法在大规模包装废弃物回收车辆路径问题上具有更优的求解性能。仿真实验结果表明，ISISS是一种求解多目标大规模包装废弃物回收路径规划问题的较优算法。

逆向物流；带时间窗和回路的车辆路径问题；分散搜索；局部搜索

绿色包装产业发展是加快推进我国生态文明建设的重要一环。2020年11月，国家发展改革委、国家邮政局等八部门联合发布了《关于加快推进快递包装绿色转型的意见》，明确提出“规范包装废弃物回收和处置”及“提升快递包装可回收性能”等要求。废弃包装品回收路径规划属于逆向物流车辆路径问题，是对传统车辆路径问题的扩展[1-3]，具有重大的社会意义。快消连锁餐饮网点的食品级包装固体废弃物具有材料同质、回收量小、批次多且分布不均等特点，企业对包装固体废弃物的回收循环利用从一定程度上缩减了生产中的物料成本，在提升经济效益的同时实施绿色制造，实现了社会效益的增长。由此可见，基于逆向物流理论，研究包装废弃物回收路径规划、科学安排运输回收路线具有较大的现实意义。

带回路和时间窗的逆向物流车辆路径问题（RL-VRPBTW，Reverse Logistics Vehicle Routing Problem with Backhauls and Time Windows）属于大规模组合优化问题。Anily等[4]证明逆向物流VRP问题属于NP难题，精确算法难以在有效时间内求解该类问题，而经典启发式算法也只能在数据规模较小时求得一个近优解。随着遗传算法、蚁群算法等进化计算方法的出现，逆向物流车辆路径问题的求解有了新方向。文献[5]基于贪婪算法，设计了初始解改进遗传算法，以求解包装废弃物回收车辆路径问题。文献[6]设计了改进蚁群算法，以求解逆向物流车辆路径问题。文献[7]考虑了CO2排放量因素，构建了逆向物流车辆短路径优化模型，并结合局部搜索和果蝇算法求解。文献[8]构建了考虑货架寿命的配送车辆路径优化模型，通过改进遗传算法进行求解。以上研究将进化计算与逆向物流问题结合，从最小化运输成本角度出发建模求解，有效验证了进化算法在解决逆向物流VRP问题上的计算能力。以上研究未在回收路径的规划过程中考虑车载容量是否有利于回收旅程的问题，因此还需进一步研究。

分散搜索[9]（Scatter Search, SS）是一类新型优化算法框架，它基于种群的全局搜索策略，利用一系列子方法构建新解，既可以提高搜索的集中性，又可以保持种群的多样性。近年来，将SS与其他搜索策略相结合，被广泛应用于求解复杂的生产计划调度问题[10-12]。在VRP问题的研究中，文献[13]利用分散搜索算法，求解同时送取货的随机旅行时间车辆路径问题。文献[14]设计了分散搜索算法，以求解多配送中心车辆路径问题。文献[15]提出一种基于分散搜索的自适应记忆编程技术，以求解多商品多变体的取货车辆路径问题。文中针对连锁餐饮快消企业对低值固体废弃包装品的回收需求，以最小化车辆运输成本、回收中心发车成本及时间窗提前或拖期惩罚为联合优化目标，建立整数规划模型，基于运输与回收协同的理念，引入“车辆剩余空间回收能力”改进节约里程算法（Clarke-Wright, C-W）[16]求得初始解，然后利用局部搜索策略对初始解进行多样化处理，最后根据分散搜索框架设计基于初始解改进的分散搜索算法进行求解。

1 问题描述与模型建立

1.1 问题描述

可以将连锁餐饮企业低值废弃包装回收问题抽象为一个考虑时间窗约束的带回路的逆向物流车辆路径问题（RL-VRPBTW）。具体描述如下：完全连接网络=(0,)，其中节点集合为0，节点0表示回收中心，集合=0{0}表示回收节点集合，中各节点均有回收需求P，且每个节点的需求服务受到时间窗[E,L]的约束；有向边集合是0的二元子集，∈，(v,v)。假设车辆载重在回收过程中不变，车辆在有向边(v,v)上匀速行驶，且所有车辆的载重上限相同，每辆车的行驶总时间不超过事先确定的最大值；车辆从回收中心空车出发，从回收点取货，每个回收点有且仅有1辆车服务1次；不考虑车辆在回收点的服务时间，车辆如提前于时间窗到达回收点，需等待；当超过车载上限或最大行驶时间限制时返回回收中心，直到服务完所有回收点。废弃包装回收路径规划需要解决的问题是在满足所有节点回收需求、时间窗约束、车辆载重限制及车辆行驶时间限制等前提下，如何安排车辆的行驶路径，使得回收中心的回收成本最小。

1.2 符号说明

符号说明：表示所有回收点集合；0表示区域内所有节点集合，节点包括回收中心和回收点，0∪{0}；表示所有车辆集合；D表示2个节点与之间的欧几里得距离，其中∈0；v表示车辆在节点与之间的行驶速度；t表示车辆在节点与之间的行驶时间，t=D/v；C表示车辆在节点与之间的行驶成本，假设车辆的单位行驶成本为1，则有C=t；C表示车辆的发车成本；P表示回收点的回收量；[E,L]表示节点的时间窗，其中[0,0]为回收中心节点0开启服务的时间窗；q表示车辆访问完节点后在访问节点之前的载重量；Q表示车辆的载重上限；B表示车辆行驶的总时间上限；表示回收中心允许选择的最小车辆数量；表示提前到达的惩罚系数；表示延期到达的惩罚系数。

定义决策变量：x表示0-1变量，车辆从节点行驶到节点时为1，否则为0；z表示0-1变量，节点由车辆服务为1，否则为0；t表示车辆到达节点的时间。

以上描述中，∈0，∈,且=|0|，=||。

1.3 数学模型

考虑上述问题，建立模型，见式（1）～（12）。

s. t.

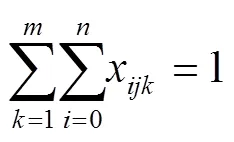
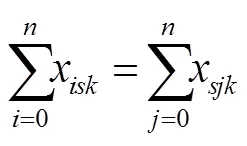
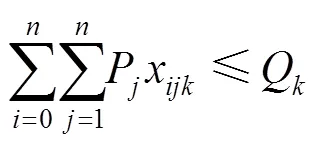
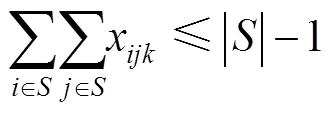
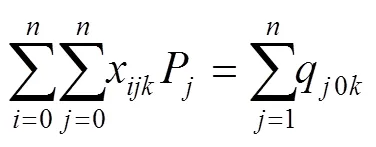
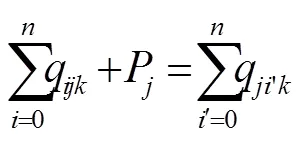
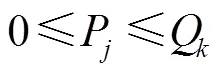
(11)

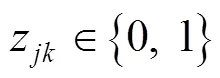
其中，式（1）为目标函数，由3个部分构成，第1部分为回收中心的发车成本；第2部分为车辆的回收成本；第3部分为软时间窗惩罚，对不能按要求到达回收点（提前或拖期）的情况给予惩罚。式（2）确保每个回收节点都会被服务1次且仅有1次。式（3）确保到达每个节点并离开的是同一辆车。式（4）确保车辆从回收中心出发，最终返回回收中心。式（5）表示车辆上的回收总数量不超过载重限额的约束。式（6）确保车辆的总行驶时间（包括提前到达的等待时间）不超过行驶时间上限。式（7）表示奇异子回路排除约束。式（8）确保车辆的最终回收载重量等于它访问的所有回收点回收数量之和。式（9）表示车辆在访问节点前后的载重量约束。式（10）确保每个节点的回收量不大于车载上限。式（11）～（12）表示决策变量取值范围约束。

2 算法设计

在分散搜索框架下，基于初始解改进的分散搜索算法（Initial Solution Improvement Scatter Search algorithm, ISISS）由5个计算步骤组成，分别是多样性产生、参考集更新、子集产生、子集合并和解改进等。SS只是一个柔性框架，其中每个步骤都可以根据实际问题利用多种方法实现，这就使SS在拥有进化算法交叉和变异等功能的同时，还可以通过控制分散和收敛聚集，提升算法的收敛性和全局覆盖能力。

2.1 多样化初始解

采用含0的整数编码方式，0表示回收中心，自然数为路径上回收点的编号。比如编码0102030405060708090，表示解中有9条路径，每条路径上只有1个回收点。

首先利用改进的节约里程算法生成模型的一个初始解，记作CW解。节约里程算法的基本思想：首先，使每个回收点与回收中心单独连接，构造出(−1)条路径；然后，基于三角不等式关系，对初始解进行缩小总距离处理，基于路径间合并可以节约距离，计算任意2个回收点组合对应的节约值Save()，将所有节约值从大到小排序，依序构造路线，对满足条件的回收点进行连接，直到满足约束条件为止，得到问题的一个CW解。

文中主要研究废弃包装回收问题，将节约值统一在时间尺度上进行考量，同时将车辆行驶过程中的“剩余空间回收能力”引入节约值的计算，即越有利于接下来回收装载的回收点，应该尽早插入当前回收路径中，根据行车运输时间和回收点的回收量计算回收点两两之间的节约值，见式（13）。

式中：Save()为路线上插入回收点后的节约值；()为2个回收点间的行驶时间；λP表示从回收中心出发，仅访问回收点的车载空间损失（或收益）；为惩罚因子。

必须指出，以上节约里程算法只能生成一个较好解，且不能作为进化算法的初始解集合，需设计多样化策略，形成初始解集合。这里通过随机交换CW解中任意2个回收点的方法，产生个初始解。由于采用含0的编码方式，在CW解中任意交换回收节点可能导致生成的新解不满足模型的约束条件，必须重新根据车载上限约束式（5）和行驶时间最大上限约束式（6）等，对产生的新解进行修复。由于回收点的位置选择具有随机性，所以在保证初始解是较好解的同时，随着回收点规模的增大，还可以保证初始解的多样性。

2.2 参考解更新

参考集由高质量的解子集1和多样性解子集2两部分构成。1由整个种群的解目标值从小到大排序决定。2根据种群中所有解与高质量解子集的距离决定，距离越大则多样性越好。参考集更新步骤如下。

1）根据目标函数，计算整个种群所有解的目标值，并从小到大排序，取前|1|个解，加入参考集中。

2）计算种群中剩余解(−1)与子集1中解的距离。遍历种群的所有剩余解，对于任意一个剩余解，计算解中所有有向边的数量，记作s。计算高质量子集1中任意一个解所有有向边的数量，记作s，并计算解与解中相同的边数量，记作s。根据式（14）计算剩余解对于高质量解集合1的距离。取剩余解中距离最大的|2|个解加入参考集中。

2.3 子集产生与子集合并

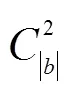
1）首先去掉每个子集2个解中的所有0，在回收节点长度范围内随机产生一个交换基因位。

2）保留其中一个解的前段，并在另一解中去除已保留的回收节点，将剩余的回收节点按原顺序排于保留路径之后。具体合并过程如图1所示。

3）根据车载上限，车辆最大行驶时间上限等约束在新解中重新插入0。

4）比较原解1、原解2、新解1、新解2的目标值，保留目标值最小的那个解到下一代种群。

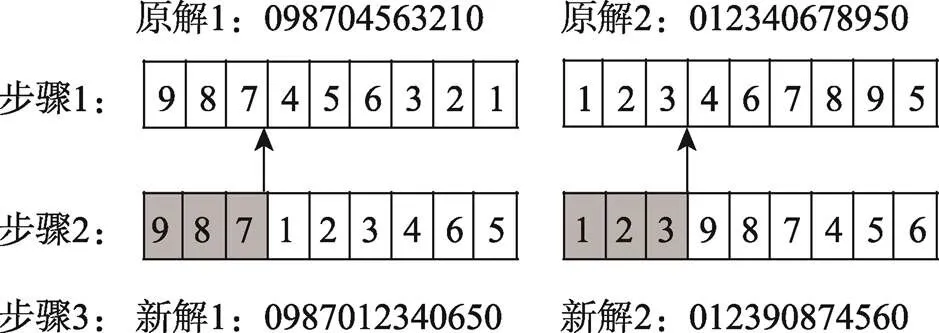
图1 子集合并过程

2.4 解改进方法

由于文中采用含0的编码设置，因此在解的改进时可以考虑“路径内部”的随机交换回收点（局部搜索策略1），以及“路径之间”的随机交换回收点（局部搜索策略2）这2种局部搜索改进策略。

2.4.1 局部搜索策略1

遍历整个种群，针对种群中的任意解进行如下步骤。

1）随机选择一条回收路径上的2个不同的点，如果2个回收点之间含0，或者回收点本身为0，则继续随机选择。

2）将行驶路径上这2个回收点之间所有回收点的车辆行驶方向逆转，得到一个新解。

3）计算新解的目标值，如果目标值优于原解，则保留新解；否则不保留此新解。

局部搜索策略1只在解的一条路径内部进行，因此不需要考虑车辆的最大负载上限和车辆最大行驶时间上限等约束，相当于在原解的邻域进行搜索，在解改进时不考虑会产生非可行解的情况。

2.4.2 局部搜索策略2

遍历整个种群，针对种群中的任意解进行如下步骤。

1）随机选择2条回收路径上的2个非0回收点，交换回收点在解中的基因位置。

2）去掉解中所有的0，采用穷尽车载上限及最大车辆行驶时间的方式，即能够纳入前一辆车的回收点尽量纳入前一条行驶路线，重新插入0，得到一个新解。

3）计算新解的目标值，如果目标值优于原解，则保留新解；否则不保留此新解。

局部搜索策略2在一个解的多条路径之间随机选择交换点，扩大了搜索空间中这个解的邻域范围。由于交换路径间的回收点可能导致车载上限或车辆最大行驶时间上限等约束不满足的情况出现，所以需要重新判断解的可行性，对非可行情况进行修复。

3 仿真实验

为了验证文中提出的ISISS算法在包装废弃物回收路径规划问题中的有效性，以“部分回收点分布较密集”的类似市区分布为地理场景，针对连锁餐饮快消企业对低值固废包装品的回收需求量级，利用Dethloff[17]和Solomon[18]提出的测试数据和时间窗生成方法，随机生成分别包含50、100、200个回收点的3种规模，且最小车辆数为3或8的各10组样本数据进行仿真实验。

3.1 算例生成方法

以100个回收点测试规模为例，在“部分回收点分布较密集”的地理场景下，利用Dethloff随机测试算例生成方法，首先在区间[0, 100]的二维正方形区域内，以均匀分布方式随机生成50个回收点的坐标；50个回收点坐标在[100/3, 200/3]的二维正方形区域内，以均匀分布方式随机生成，从而在1/9的区域内生成密集的市区配置地理场景。由于这里只考虑了回收问题，每个回收点的废弃包装回收量P=（0.5+r）R，其中R为均匀分布在[0, 100]之间的整数，r为[0, 1]之间的随机数。由此，确定每个算例的车载限额=∑P/。其中，∑P表示所有回收点的回收总量，为允许选择的最小车辆数量，这里选择为3或8生成算例。本算例的数据无实际物理意义，是在[0, 100]区间生成的，因此相应的目标值也无量纲。

关于时间窗的生成，参照Solomon提出的VRPTW基准数据生成方法，时间窗的中间值在区间(00,i,0-t,0)中随机生成，且时间窗宽度为标准正态分布随机数，其中[0,0]为回收中心进行回收服务的时间窗，0, i和t,0分别表示车辆从回收中心到回收点的行驶时间和该回收点回到回收中心的行驶时间。在模型中假设回收中心时间窗[0,0]为[0, 24]，所有车辆的发车成本C为50，所有车辆的行驶速度v为60，提前到达或延期到达回收点的惩罚系数、均为1。

3.2 算法比较

为了验证ISISS算法的求解性能，与改进的节约里程（C-W）、分散搜索（SS）和遗传（Genetic Algorithm, GA）等3种算法进行对比。其中，SS和GA的初始解均采用随机初始解，GA的交叉率c为0.6，变异率m为0.1，种群规模为100，运行代数为20 000；SS和ISISS算法的参考集|=20，其中较好解集|1=10，多样解集|2=10，种群规模为100，运行代数为100。由于GA与SS算法在迭代方式上存在不同，2种算法无法基于相同的迭代次数进行比较，因此将2种算法在种群规模相同且运算时间大致相同的前提下对不同规模的算例进行比较。对比了3种规模下，最小车辆数量分别为3或8的各10组数据目标值平均计算结果，如图2所示。

图2 3种规模下目标值的比较

由图2可知，相对于改进C-W算法生成的较好解，其他3种进化算法的求解优势明显。当回收点数量为50时，GA求得的目标值仅略优于C-W算法，而SS和ISISS算法求得的目标值明显优于C-W，说明在相同的数据规模和计算复杂度下，ISISS算法能够充分发挥参考集更新和解改进等策略的优势，但ISISS相对于随机初始解SS的改进效果并不显著。当回收点数量扩大为100时，选择较大的车型（3）时，ISISS相对于GA的改进幅度达到了65.8%，相对于SS的改进率也很明显；选择较小车型（8）时，ISISS相对于SS的改进效果仍不够显著。随着数据规模的进一步扩大，当回收点为200时，ISISS算法在2种车型选择下的改进效果才显示出来。由于ISISS在初始解生成时就采用C-W启发式算法生成了较好的初始解，并在此基础上进行了多样化处理，因此ISISS具有更优的多样性解和较好解，从而增强了算法的寻优能力，更加适合于求解大规模回收车辆路径问题。

另一方面，从4种算法得出的发车数量（表1）比较结果可以看出，在不同规模下，C-W算法都可以得到较少的发车数量，但这是以高额的时间窗惩罚和回收成本为代价，ISISS算法可以在同时考虑回收成本和时间窗惩罚的基础上，将回收中心总发车数量控制在一个较小的数量上。当回收点为50、100时，ISISS得到的发车数量（4、9）仅比对应的最小车辆数（3、8）多1辆车，而随机初始解的GA和SS都无法达到这个发车数量，说明对于同一个回收路径规划问题，ISISS可以更好地发挥已派出车辆的装载率，从而降低总用车数量。

文中将时间窗惩罚引入优化目标，而非单纯采用运输成本。表2列出了GA、SS、ISISS等3种算法在不同数据规模下3个具体算例C50-3、C100-3、C200-3的目标值分项。数据表明，相对于随机初始解的GA、SS算法，ISISS算法能够得到更优的可行解，找到了满足约束且在不同的目标上表现更好的解。当回收点数量较小时，ISISS在运输成本和提前拖期惩罚2项目标值上比随机初始解SS略有改进，但并不明显；当回收点数量增至200时，ISISS除了能达到更好的运输成本，同时还能尽可能地满足不同回收点服务时间窗的要求，大幅降低了时间窗提前拖期惩罚目标，并减少了发车数量，降低了发车成本。

表1 发车数量比较

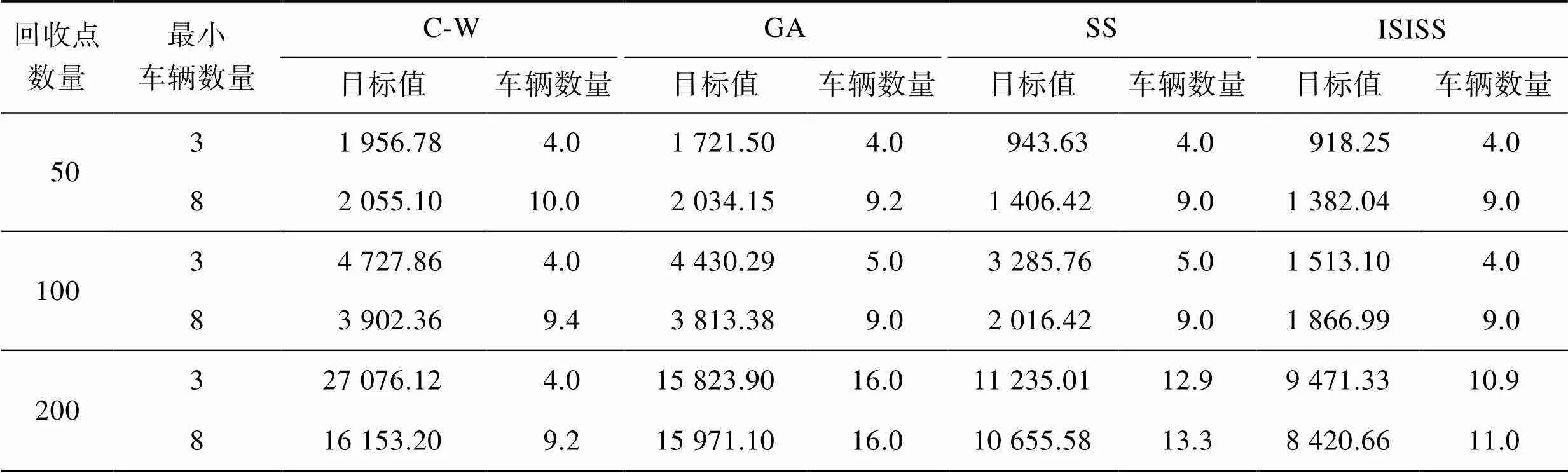
Tab.1 Comparison of the number of departures

表2 基于算例C50-3、C100-3、C200-3的3种算法目标值分项比较

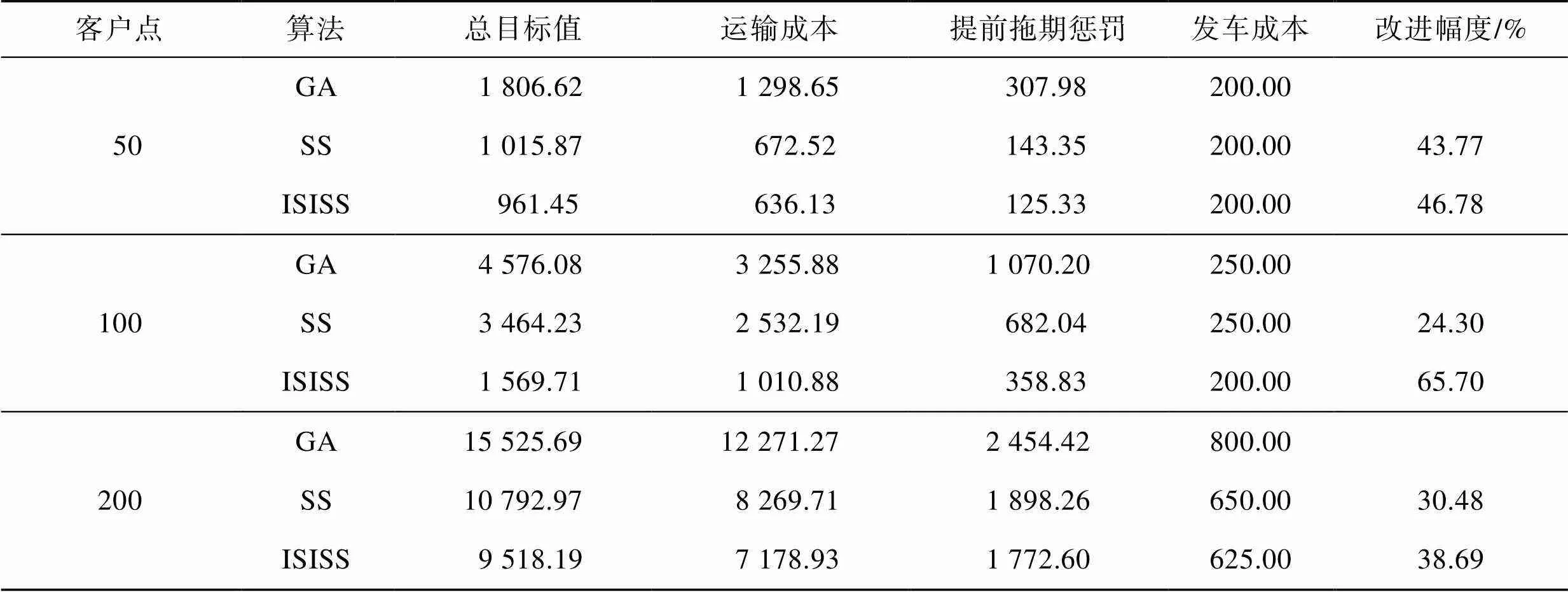
Tab.2 Itemized comparison of the objective values based on C50-3, C100-3 and C200-3

3.3 路线明细

在回收点为100、最小车辆数量为3时，算例C100-3的一次路径规划明细如表3所示，对应的回收路径规划如图3所示。

表3 算例C100-3路径排序

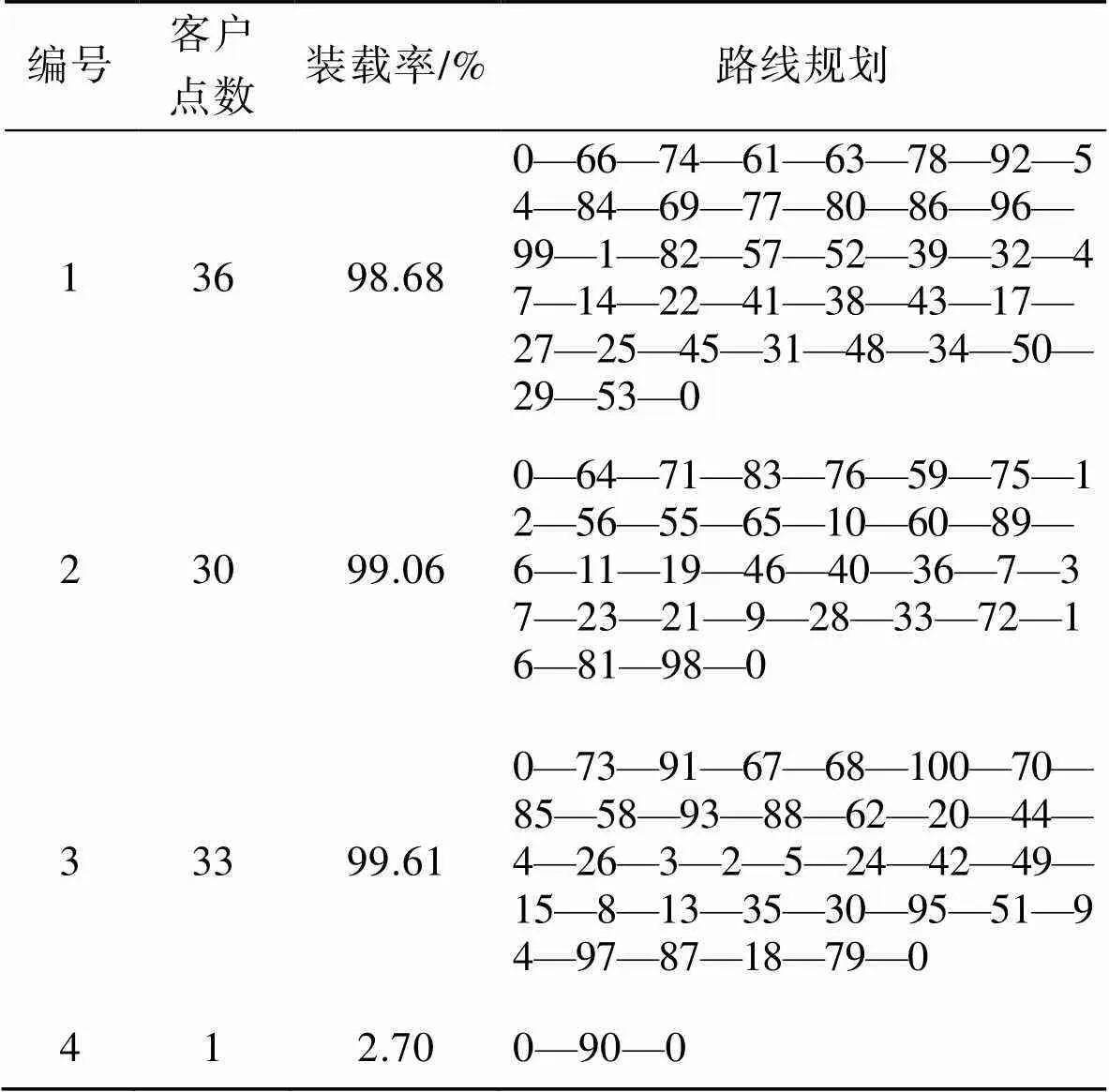
Tab.3 Route sorting of C100-3

图3 ISISS求得算例C100-3的一个较好解

随着回收点数量的增多，ISISS算法仍然可以将规划车辆数控制在4辆车，前3辆车的车辆负载都尽可能充分利用，基本接近车载上限，且从路径规划（图3）可以看出，在“部分回收点分布较密集”的地理场景下，ISISS算法能够在一辆车的路径规划上兼顾市区密集部分点和郊区零散分布点，各条路径彼此重叠覆盖的区域较少，且各条路线上的交叉回路较少。在相同的回收点分布下，选择较小的车型（8）时，算例C100-8的路径规划如图4所示，对应的路径排序如表4所示。

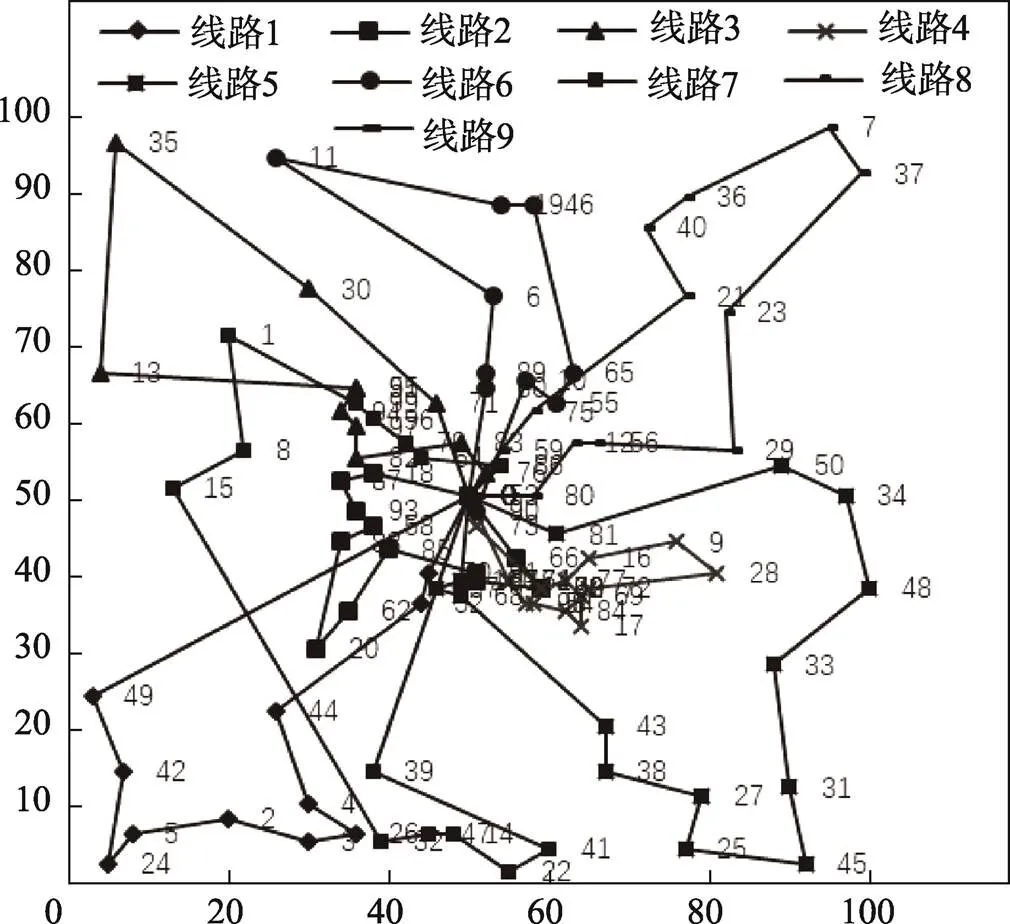
图4 ISISS求得算例C100-8的一个较好解

表4 算例C100-8路径排序

Tab.4 Route sorting of C100-8

4 结语

从废弃包装品回收的实际问题出发，研究了逆向物流车辆路径规划问题，将软时间窗约束转化为逆向物流车辆路径问题的优化目标，以最小化运输成本、发车成本和时间窗惩罚成本为目标，建立了带回路的车辆路径问题联合优化数学模型。采用含0的整数编码，同时考虑车辆旅行时间节约值和车辆剩余回收空间收益两方面因素，确定节约值，利用改进的节约里程算法得到一个初始解，并设计初始解多样化策略，生成初始解集合。基于改进的优质多样性初始解，利用分散搜索进化算法求解。针对“部分回收点分布较密集”的类似市区型地理场景生成多组算例，在不同的数据规模下验证算法的性能。下一步将对ISISS算法在同时送取货的回收场景及考虑回收服务时间的路径规划问题进行研究。

[1] GAO Z H, YE C Y. Reverse Logistics Vehicle Routing Optimization Problem Based on Multivehicle Recycling[J]. Mathematical Problems in Engineering, 2021, 2021: 5559684.

[2] ALIZADEH FOROUTAN R, REZAEIAN J, MAHDAVI I. Green Vehicle Routing and Scheduling Problem with Heterogeneous Fleet Including Reverse Logistics in the Form of Collecting Returned Goods[J]. Applied Soft Computing, 2020, 94: 106462.

[3] HAN Y. Evolutionary Algorithms for the Heterogeneous Fleet Green Vehicle Routing Problem with Reverse Logistics Characteristics[J]. Journal of the Korean Society of Supply Chain Management, 2017, 17(2): 133-143.

[4] ANILY S, MOSHEIOV G. The Traveling Salesman Problem with Delivery and Backhauls[J]. Operations Research Letters, 1994, 16(1): 11-18.

[5] 张异. 包装废弃物回收车辆路径问题的改进遗传算法[J]. 包装工程, 2018, 39(17): 147-152. ZHANG Y. Improved Genetic Algorithm for Vehicle Routing Problem in Packaging Waste Recycling[J]. Packaging Engineering, 2018, 39(17): 147-152.

[6] 陈秀娟, 高更君, 冯媛媛. 基于改进蚁群算法的逆向物流车辆路径优化[J]. 制造业自动化, 2019, 41(5): 46-49. CHEN X J, GAO G J, FENG Y Y. Optimization of Reverse Logistics Vehicle Path Based on Improved Ant Colony Algorithm[J]. Manufacturing Automation, 2019, 41(5): 46-49.

[7] 赵娆, 陈志华. 基于局部搜索的逆向物流车辆最短路径优化[J]. 计算机仿真, 2022, 39(11): 215-219. ZHAO R, CHEN Z H. Shortest Path Optimization of Reverse Logistics Vehicle Based on Local Search[J]. Computer Simulation, 2022, 39(11): 215-219.

[8] 杨玮, 赵晶, 张堃, 等. 基于货架寿命的乳制品配送车辆路径优化研究[J]. 包装工程, 2019, 40(11): 72-79. YANG W, ZHAO J, ZHANG K, et al. Path Optimization of Dairy Distribution Vehicle Based on Shelf Life[J]. Packaging Engineering, 2019, 40(11): 72-79.

[9] GLOVER F. A Template for Scatter Search and Path Relinking[M]// Lecture Notes in Computer Science. Berlin: Springer Berlin Heidelberg, 1998: 1-51.

[10] KALRA M, TYAGI S, KUMAR V, et al. A Comprehensive Review on Scatter Search: Techniques, Applications, and Challenges[J]. Mathematical Problems in Engineering, 2021, 2021: 5588486.

[11] 毛丽丽, 张则强, 朱立夏. 混合模拟退火及分散搜索优化过道布置问题[J]. 计算机工程与应用, 2018, 54(3): 243-249. MAO L L, ZHANG Z Q, ZHU L X. Hybrid Scatter Search Algorithm with Simulated Annealing for Corridor Allocation Problem[J]. Computer Engineering and Applications, 2018, 54(3): 243-249.

[12] 范佳静, 曹玉华, 曹敏. 基于改进分散搜索算法的多资源跨单元调度问题研究[J]. 中国机械工程, 2017, 28(22): 2722-2731. FAN J J, CAO Y H, CAO M. Study on Multi-Resource Intercellular Scheduling Problem Based on ASS Algorithm[J]. China Mechanical Engineering, 2017, 28(22): 2722-2731.

[13] 张涛, 余绰娅, 刘岚, 等. 同时送取货的随机旅行时间车辆路径问题方法[J]. 系统工程理论与实践, 2011, 31(10): 1912-1920.ZHANG T, YU C Y, LIU L, et al. Method for the Stochastic Traveling Time VRPSPD Problem[J]. Systems Engineering-Theory & Practice, 2011, 31(10): 1912-1920.

[14] 张鹏威, 李英, 成琪. 有限充电设施下的多配送中心电动车辆路径问题研究[J]. 工业工程与管理, 2019, 24(5): 97-105. ZHANG P W, LI Y, CHENG Q. Multi-Depot Electric Vehicle Routing Problem under Limited Recharging Infrastructures[J]. Industrial Engineering and Management, 2019, 24(5): 97-105.

[15] EUCHI J. Hybrid Adaptive Memory Programming to Optimize the Multi-Commodity many to many Vehicle Routing Problem[J]. International Journal of Mathematics in Operational Research, 2020, 1(1): 1.

[16] CLARKE G, WRIGHT J W. Scheduling of Vehicles from a Central Depot to a Number of Delivery Points[J]. Operations Research, 1964, 12(4): 568-581.

[17] DETHLOFF J. Vehicle Routing and Reverse Logistics: The Vehicle Routing Problem with Simultaneous Delivery and Pick-up[J]. OR-Spektrum, 2001, 23(1): 79-96.

[18] SOLOMON M M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints[J]. Operations Research, 1987, 35(2): 254-265.

Improved Scatter Search Algorithm to Solve Packaging Waste Recovery Vehicle Routing Problem

ZHANG Qiqi,CHEN Qun*

(Shanghai Publishing and Printing College, Shanghai 200093, China)

The work aims to summarize the packaging waste recovery routing as a reverse logistics vehicle routing problem with back path and time window (RL-VRPBTW), so as to construct a model with the minimum recovery cost, departure cost and time window penalty as the joint optimization objective. A better initial solution was obtained by introducing the factor of "vehicle remaining space recovery ability" to improve the classical heuristic C-W algorithm. Based on the Scatter Search framework, a Scatter Search algorithm (ISISS) based on initial solution improvement was designed. According to the problem model, the algorithm functions were realized through five steps of diversity generation method, reference set update method, subset generation, merging method and solution improvement method. In the city-type geographical scenario of "dense distribution of some recovery points", three scale examples with 50, 100 and 200 recovery nodes were randomly generated, and two vehicle types were considered for simulation experiments. The ISISS algorithm was compared with C-W, GA and SS algorithms to verify that the algorithm proposed had better performance in solving the routing problem of large-scale packaging waste recovery vehicles. The simulation results indicate that ISISS is a better algorithm to solve the multi-objective large-scale packaging waste recovery routing problem.

reverse logistics; vehicle routing problem with time windows and back path; scatter search; local search

TP301；TB498

A

1001-3563(2024)09-0193-08

10.19554/j.cnki.1001-3563.2024.09.025

2023-06-28

国家社科基金（18BT058）；国家新闻出版署“智能与绿色柔版印刷”重点实验室项目（KLIGFP-01)；上海市东方学者特聘教授基金（TP2022126）