以核心素养为导向的高中数学试题命制的实践与思考——以一道以“隐圆”为背景的解三角形多选题的命制为例

广东省佛山市第一中学(528000) 王彩凤

数学学科核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析,是思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学的学习和应用过程中逐步形成和发展的[1].为发展学生的核心素养,教师需要引导学生去理解数学知识的本质,提高应用意识,而不是让学生机械地背诵知识和解题方法.高质量的试题会具有较强的导向性,所以,数学试题的命制应以核心素养为导向,关注数学的本质,考查学生的能力和核心素养.笔者在参加“命题·评题·品题”比赛中,命制了一道以“隐圆”为背景的解三角形多选题,命题过程印象深刻,获益匪浅.本文以此题的命制为例,谈谈以核心素养为导向的高中数学试题命制的步骤与策略.

1 命题构思

1.1 明确要求

解三角形与“隐圆”知识之间存在密切联系,命制的解三角形多选题以“隐圆”为背景,围绕三角形的边、角、面积等元素设计问题,题干力求简洁,考查正弦定理、余弦定理、基本不等式、平面向量、圆等相关知识.试题的求解突出强调学生对三角形和圆的基础知识、基本方法的深入理解和灵活应用,难度为中档偏难.

1.2 命题立意

依据新课程标准的要求,数学试题的考查内容不仅要聚焦学生对重要数学概念、定理、方法、思想的理解和应用,还应适度增加试题的思维量,发挥人才选拔功能[1].以“隐圆”为背景的解三角形多选题的命制,注重考查学生综合应用知识的能力,要求学生能突破原有思维的禁锢,挖掘题目中变与不变的量,创新性地解决问题.试题考查了转化与化归、函数与方程等数学思想方法,考查了学生的直观想象能力、逻辑推理能力、运算求解能力、创新能力等关键能力,考查了直观想象、逻辑推理、数学运算等核心素养,体现基础性、综合性和创新性的考查要求.

2 试题的命制过程

2.1 设计思路

以“隐圆”为背景的解三角形试题的命制,拟以多三角形组合的模型作为研究的载体,围绕三角形的边、角、面积等元素设计题目条件和问题.解答者既可以利用正弦定理解三角形,也可以借助题目中定长、定角条件构造辅助圆,创新性地解决问题.

2.2 选材研究

根据设计思路,笔者重点研究了2020 年新高考数学全国II 卷第17 题,并以此题为基础进行创作.

原题(2020 年新高考数学全国II 卷第17 题)ΔABC中,sin2A-sin2B-sin2C=sinBsinC,(1)求A;(2)若BC=3,求ΔABC周长的最大值.

图1

解法1、2 是常规的解题思路,解法3 在解答题中应用虽然不够严谨,但其关注到边角之间存在的联系,根据定角构造辅助圆这一做法,若能应用于选择题或者填空题,则可极大降低运算量,提高思维量,又可考查学生的空间想象能力、创新解决问题的能力.受此题启发,笔者以“隐圆”为背景,命制了一道解三角形多选题.

2.3 联系与搭架

2.3.1 确定三角形模型

命题初步设想,基于“爪型”三角形模型,通过设定合适的边角条件,构造辅助圆,探求三角形中角度、边长与面积的最值问题.如图2,“爪型”三角形之“中线模型”,可以构造以D为圆心,以AB为直径的圆;如图3,“爪型”三角形之“角平分线模型”,可以分别构造ΔACD和ΔBCD的外接圆;如图4,“爪型”三角形之“高模型”,可以构造ΔACD的外接圆.

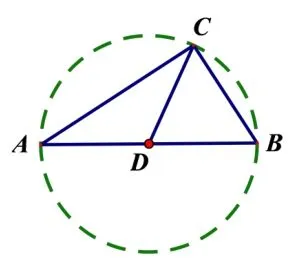
图2

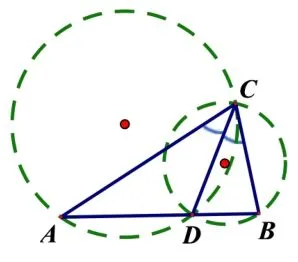
图3

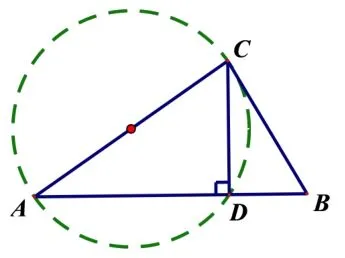
图4

在以上“爪型”三角形模型中,均可以“隐圆”为背景设计问题.但这些设想已经有很多现成的题目,笔者想在此基础上进一步创新命题,选择了图5 的多三角形模型作为命题的基础模型.

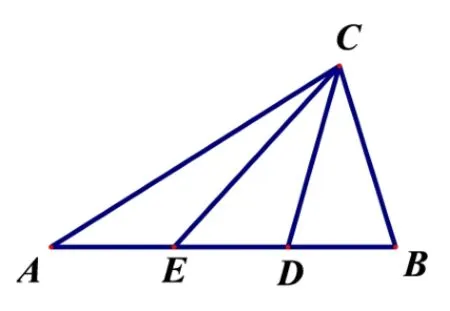
图5

2.3.2 问题的确定

题干设计为: 如图5,ΔABC中,AB=,点D,E为AB的两个三等分点.

图6

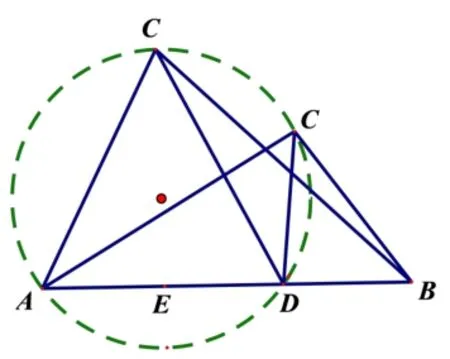
图7

图8

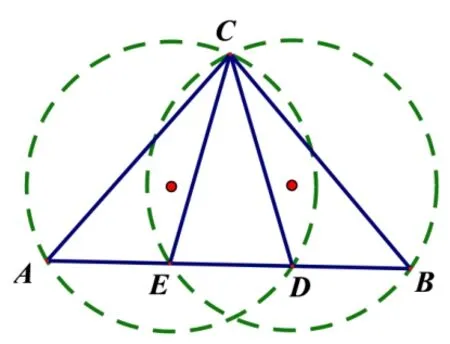
图9

从A 到D 选项,试题设计简洁新颖,呈现出入口宽、起点低、坡度缓、尾巴翘的特点,方法多且具有明显的层次性,体现“多思少算”的命题理念,既考查了学生的基础知识、基本思想方法,又考查了学生的空间想象能力、逻辑推理能力和创新解决问题的能力.

2.3.3 确定成题

多选题如图10,ΔABC中,AB=,点D,E为AB的两个三等分点.以下说法中正确的是( ).

图10

参考答案A,B,D.

2.4 解答分析

2.4.1 思路分析

对于A 选项,可用代数法,利用余弦定理和方程思想求出AC,BC之间的关系式,再代入

由此判断ΔABC为钝角三角形.也可用几何法,观察图形发现CD=DE=DB,则点C在以D为圆心,以BE为直径的圆上运动(不与B,E重合),从图中可以直观地看出∠ACB为钝角.

对于C 选项,利用正弦定理将边化为角,将BC长度的最值转化为三角函数的最值问题;也可以像B 选项的解法3一样,根据定角∠ACD构造ΔACD的外接圆,则点C为优弧上的动点,当C在BO的延长线上时,此时BC的长度最大.

对于D 选项,第一种解法是分别在ΔCED和ΔACD中应用正弦定理,通过共同边CD建立方程求解;第二种解法是根据面积等量关系=2 建立方程求解;第三种解法是根据ΔABC的对称性建立平面直角坐标系,求出ΔACD和ΔBCE的外接圆方程,联立两圆方程求出点C的坐标,再应用数量积公式求解cos ∠DCE.

2.4.2 解法呈现

对于A 选项,设∠A,∠B,∠ACB所对的边分别为a,b,c,有以下两种解法.

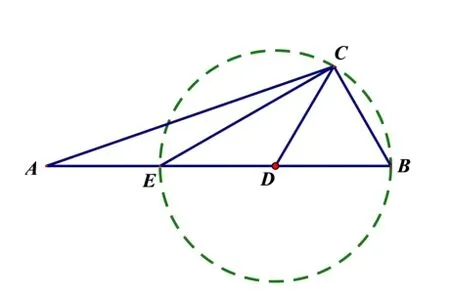
图11

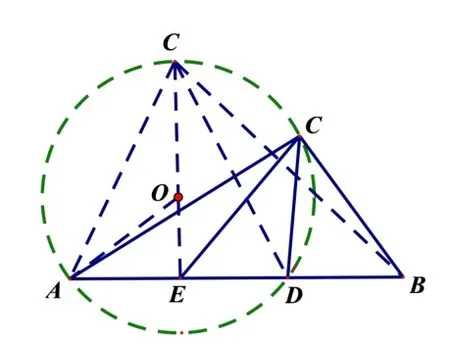
图12

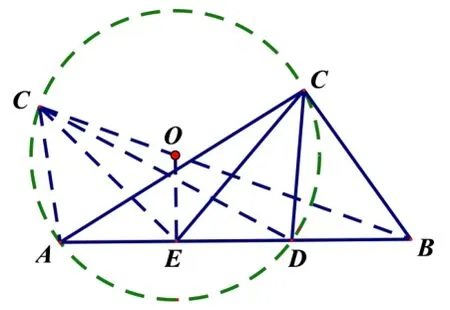
图13

对于D 选项,有以下三种解法.

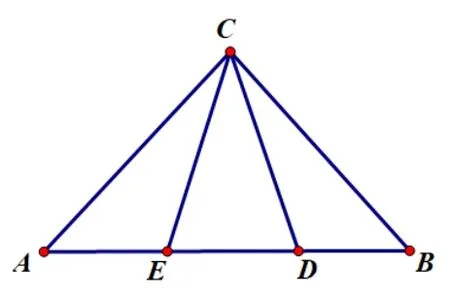
图14

图15

故D 正确.

3 试题的评价分析

解三角形多选题的命制,立足于高考试题,以“隐圆”为背景,以数学学科核心素养为导向,考查了正弦定理、余弦定理、基本不等式、平面向量、圆等基础知识,难度中档偏难,对学生的综合能力要求较高.本题在解题方法上具有多样性,鼓励思维创新,引导学生在解三角形时,要关注的首先是几何的关系,然后才是函数与代数的关系[2],要求学生能以整体的视角审视问题,抓住问题本质,迁移思想方法,创造性地解决问题.本题考查了转化与化归、数形结合、函数与方程等数学思想方法,有助于提升学生的直观想象、逻辑推理、数学运算和数学建模素养(见表1).

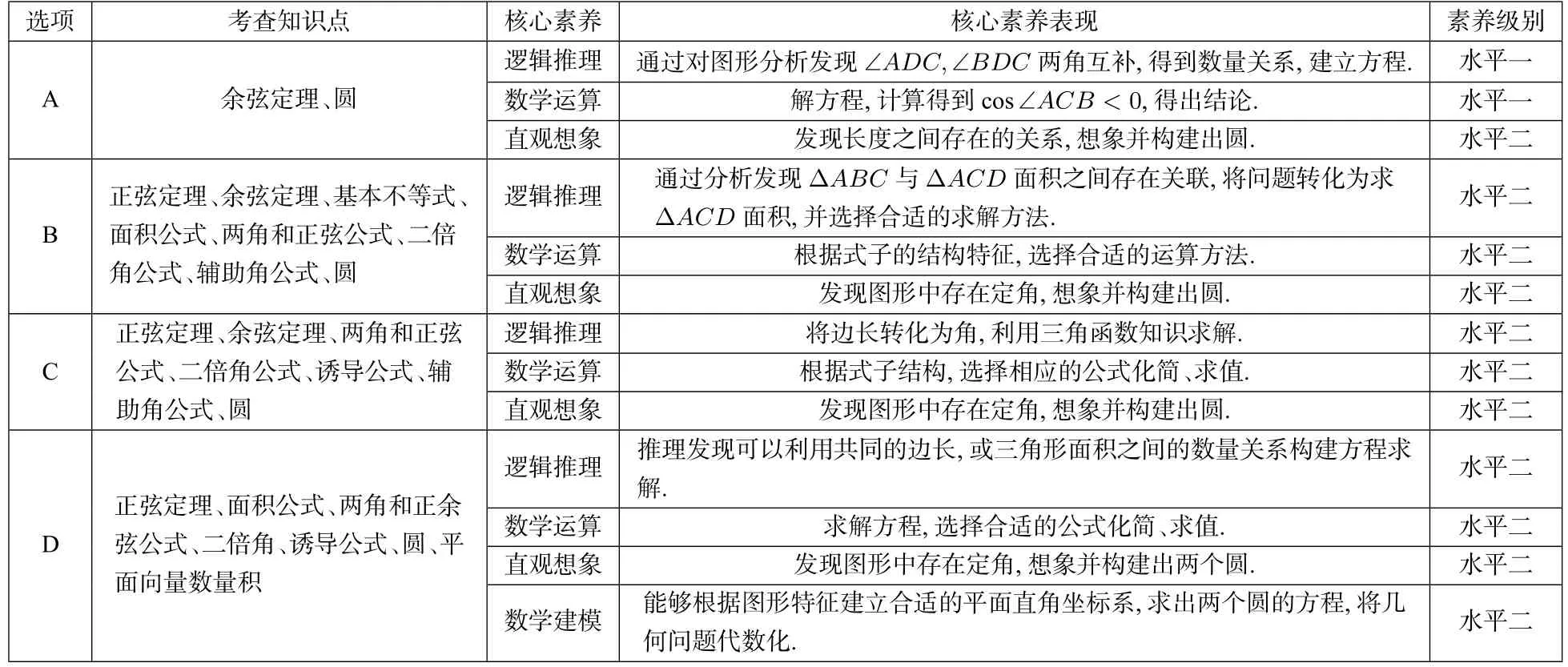
表1 数学学科核心素养的表现及其级别

4 命题反思

4.1 立足基础,素养导向

试题的命制需要立足基础,依据《普通高中数学课程标准(2017 年版)》所规定的内容和要求,以核心素养为导向,创建合理的问题情境,设计的问题不仅要考虑知识点的覆盖面、题目的难度,也要考虑切合教学实际、符合学生的学习和生活实际.同时,问题的解决应具备入口宽、起点低、坡度缓、尾巴翘的特点,允许多角度解决问题,鼓励思维创新[3],考查学生的基础知识、基本技能、基本思想方法和基本活动经验,培养学生良好的数学思维品质,提升学生的数学核心素养.

4.2 深度研究,创新命题

试题的命制还需要在反套路、反机械刷题上下功夫,所以命题时还需要深入研究相关的知识,尽量选用新背景、新材料,或者融合知识点,创设新的问题情境,巧妙设问.对于一些经典题型,可以对其进行改造、升华或者使用新的设问方式等,变成一道新颖的题型.命题要注重引导学生去理解数学知识的本质,提高学生的知识迁移能力、逻辑推理能力和创新能力.

4.3 反思自身,提升能力

研究命题是教师的一项重要工作,不仅能加深教师自己对所教知识的理解,同时也可以为课堂教学提供服务.要命制好一道题,并不容易,教师必须要认真研读《普通高中数学课程标准(2017 版)》的要求,研究教材、研究教法、了解学情,明确知识和能力的考核点.同时,教师在教学或者解题的过程中,要收集积累对自己有用的素材,不断充实完善自己的理论知识库,提升研究能力,才能更好地命制出科学的、有创造性的、有针对性的试题,进而以题来引领教学,切实提高课堂教学质量.