一道圆锥曲线压轴题的探究与推广

张家港市凤凰高级中学(215000) 姜之聪

南京航空航天大学苏州附属中学(215000) 李文博

探索性问题历来倍受高考青睐,它有利于考察学生的思维品质和学习潜能;有利于培养学生发现问题、分析问题、解决问题的能力和创新意识.一个探索性问题,往往蕴含丰富的数学知识、性质,常是学习者探求一类问题的“窗口”.本文以一道某地高三模考中的圆锥曲线压轴题为例,探究推广出该类问题的一般性结论,希望能带给读者些许收获.

1 试题呈现,探究问题本质

题目已知A,B分别是椭圆=1 的左右顶点,过C的右焦点的直线l交C于D,E两点,过点D作直线:x=4 的垂线,垂足为F,直线lEF与C的另一个交点为G.

(1)直线lEF是否过定点? 若是,则求出该定点;若否,则请说明理由;

(2)求直线lAE与直线lBG交点的横坐标.

2 纵向推广,归纳一般结论

上述试题研究的是椭圆的一种特殊性质,根据由特殊到一般的数学思想,可得下述两条结论:

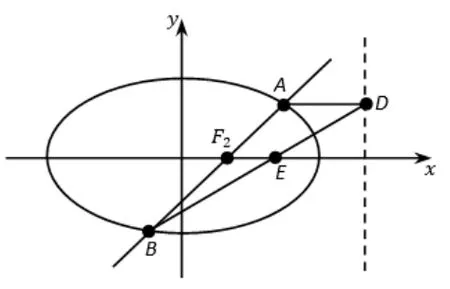
图1

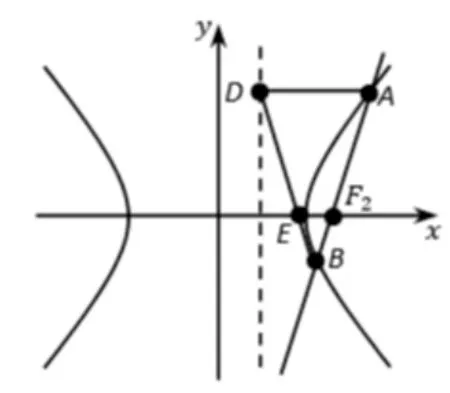
图2

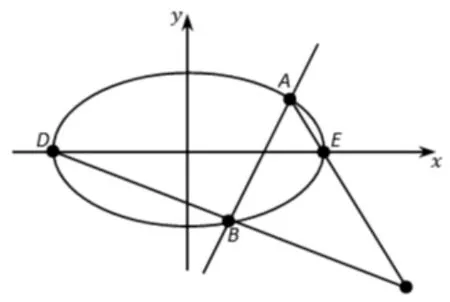
图3

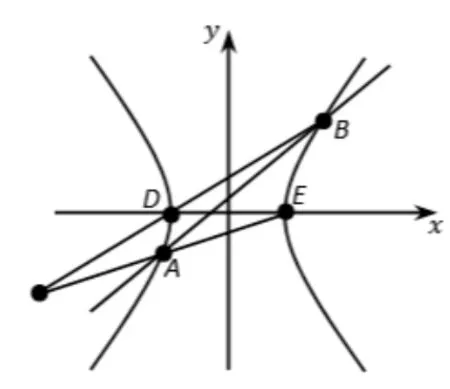
图4

3 试题演练,熟练解题技巧

(1)求双曲线C的标准方程;

(2)经过点F2的直线l与双曲线C交于A,B两点,过点A作直线x=2 的垂线,垂足为D,过原点O作OM⊥BD,垂足为M.则在x轴上是否存在定点N,使得|MN|为定值? 若存在,求出点N坐标;若不存在,请说明理由.