基于直观想象素养视角的高中解析几何概念教学实践研究

摘 要：本文以解析几何抛物线定义及其标准方程为例，深入研究教学中直观想象的渗透，进而分析如何有效培养学生的直观想象素养.

关键词：数学教学；直观想象；核心素养；教学实践

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2024）06-0035-03

直观想象是指运用生活中实际情境，利用图形直观感知，借助几何直观和空间想象感知事物变化，从而认识、了解并解决相应数学问题的素养.培养学生的直观想象能力是教学中一直热议的话题，本文以解析几何抛物线定义及其标准方程为例，深入研究教学中直观想象素养的渗透和培养.

1 基于直观想象的教学实践探究

1.1  确立教学目标，明确培养学生直观想象的方向

在课堂教学过程当中，整个教学过程的实施都是以教学目标为基调进行的.因此，想要培养学生的直观想象，就必须先确定所要达到的目标，这就是培养学生的直观想象能力所要达到的目的.

（1）让学生充分理解抛物线的定义，并会画出抛物线的图形，熟悉掌握抛物线的标准方程；利用定义求抛物线的标准方程、会表示抛物线的焦点以及表示抛物线的准线方程；并会简单运用.

（2）从具体的实际情境中，抽象出抛物线的模型；化抽象为具象，化无形为有形.

（3）在学习抛物线中，体会数形结合思想，用数学思维和数学方法解决与抛物线有关的生活问题.

1.2 创设情境，迸发直观洞察，激起学生直观想象的兴趣

教师在创设情境的时候，要尽可能地创设与学生实际生活相符合的情境.利用图片、视频或数学模型展示，让学生直观感受抛物线方程的产生，以最快速度理解图形，从而真正掌握抛物线的生成过程，找到数形之间的联系[1].这种利用几何图形来认识、描述和理解数学问题，再进行数学思考和分析的过程，非常符合高中生的学习特点.

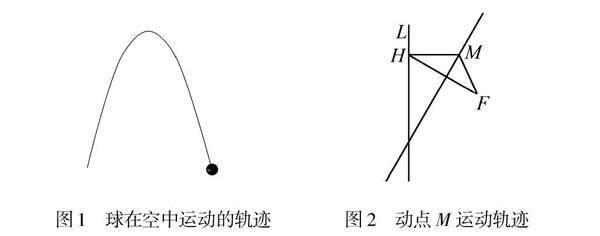
【实际情境】在本章解析几何的学习中，目前已经学习了椭圆、双曲线，通过前面的学习探究可以发现如下规律.设动点M到定点F的距离与到定直线l（不过点F）的距离之比为k.

当0

当k>1 时，点M的轨迹为双曲线；

当k=1时，即动点M到定点F的距离与动点M到定直线l的距离相等时，动点M的运动轨迹会是什么形状？

利用信息技术作图我们一起来探究，如图2，F为一定点，l是不经过点F的定直线，点H为直线l上任意一点，过点H作MH⊥l，线段FH的垂直平分线m交MH于点M.用鼠标拖动动点H，观察可以发现，点M随之运动.

通过对生活实际情境的创设，在教学实践中，可以进一步提高学生的直观发现能力，进而为后续学生直观想象素养的培养奠定了坚实的基础.

1.3 问题探究，引导学生在思考中联想到直观想象

让学生们借助三角板和直尺，亲自体验自己画出抛物线，在画图中感知抛物线必备的条件.动图展示作图过程，提出问题，可以将直尺，钉子，笔尖转化为数学模型，分别看成何种数学图形，引导学生在整个作图过程中从具体事物抽象概括出抛物线定义几几何特征.

【问题串】问题1：它的轨迹是什么形状？你能发现点M满足的几何条件吗？

（活动预设）抛物线.

问题2：你能发现点M满足的几何条件吗？

（活动预设）在平面内，通过观察发现动点M到定点F的距离与动点M到定直线l的距离相等，即|MF|=|MH|

问题3：MF，MH分别什么呢？

（活动预设）通过问题引导，让学生观察动点到定点的距离与动点到定直线的距离，将数量问题转化为几何图形，利用几何特征表达动点轨迹，从而引出抛物线的定义.

追问1：如果定点F在直线l上呢？所得到的轨迹是否依旧为一条抛物线？若不是抛物线的话，应是什么图形？

问题4：在现实中生活中，抛物线形状的图形广泛存在于现实生活中，能否开动脑筋想一想在现实生活中存在的拋物线形状都有什么？

在教学中，学生作为课堂的主体，作为教师，只是课堂中引导学生的辅助者，起着引导学生的作用.因此，在课堂中教师以提问的方式或者问题串的形式进行教学，既符合建构主义的要求，又运用了启发性原则，既能促使学生在思考问题的过程中进行知识的探索，又能帮助学生在知识的探索中联想到直观想象，为今后高中数学学习中直观想象的培养奠定了基础[2].

1.4 建立数形联系，类比其他抛物线建系，展现几何直观，构建概念

在数学问题中用几何图形表示数量关系，降低复杂数值较多的数学问题的难度；同理运用代数知识解决几何问题，通过代数运算对几何知识进行推导，使几何问题化难为易，进而找到更简便有效的解题方法，同时使学生更直观、更准确地理解几何问题.

【数形结合】问题5 对椭圆与双曲线标准方程的建立过程进行比较，你认为如何建立坐标系，可能使所求抛物线的方程形式简单？

（活动预设）（1）协同探究，以小组为单位；（2）小组探讨、画图探究，尝试多种建系方法，并在多种建系方法，仍会出现如下图3这样的3种情况.在图3中选取，何种建系会使得抛物线方程的形式最为简单.

继续观察，容易想到，x轴与抛物线的交点是图中KF的中点，可将其设置为原点.

设计意图：学生可以通过尝试画图的方式，可以直观感知如何建系使得各元素以及曲线的方程形式简单.

问题6 设焦点到准线的距离为p，（a）用p表示焦点坐标；（b）用p可否表示准线方程.（c）动点M轨迹即为抛物线，这一点满足的方程如何用p表示.

设计意图：（1）将几何问题转化为代数问题，用数量关系表示；（2）感受直接法求轨迹方程.

1.5 信息技术融合，先进的教学手段创造培养直观想象的机会

目前学生对数学软件动图动画等都很感兴趣，优化教学手段，利用几何画板和GGB等数学软件，这样可以调动学生的学习积极性.

动图展示抛物线形成过程，形象直观演示抛物线动态变化过程有效突破教学难点，引导学生分析较为复杂的动点轨迹或抛物线面积、最值等习题.如下题：

将抛物线y=1／2x2平移得到抛物线M，抛物线经过点A（-6，0）和原点O（0，0），它的顶点为点P，它的对称轴与抛物线y=1／2x2交于点Q，求图中阴影部分的面积.

由动图可知，图4左下部分面积进行可平移至图5，根据二次函数对称性可至图6，由此可知图4中阴影部分面积即为图6中矩形的面积，即3×1／2×（-3）2=27／2.

而针对一些基础比较薄弱的学生，可以考虑录制例题的微课或者定义生成的课件等提供给学生，以便于学生在课后自主学习巩固．课件或微课的动态演示，有效地展示动点M轨迹的动态过程如图7.

在讲授新课的过程中，要多注重学生的直观感知，合理利用数学软件，通过对动点轨迹形成而进行观察、推理、计算，是学生掌握理解解析几何这一部分的难点.同时引导学生多画图，教师在授课时也应注重学生作图能力的培养，才能够做到准确识图、用图、解图.并且在解题教学中，有意识地从几何直观方面渗透对学生直观想象素养的培养[3].

2 教学实践总结及教学实践反思

抛物线概念的形成是本节课的难点和重点.在教学实践中，引导学生将抛物线与所学过熟知的二次函数进行对比.通过变换坐标系的建立，一方面加强学生在求抛物线方程的计算能力，另一方面将抛物线与二次函数联系起来，让学生理解二次函数也是抛物线，知道二次函数和解析几何中抛物线的共通之处和不同的表达形式，使学生有一种“顿悟”的感觉［4］.

学生自主探究对比椭圆、双曲线、抛物线的区别与联系，自行类比四种不同抛物线的标准方程、图形焦点坐标以及准线方程.关键要让学生学会运用类比和数形结合的思想解决数学问题.教学实践结束时可采用抛物线形拱桥为背景，可以使学生再一次直观感受抛物线的形成［5］.

在例题的基础上增加了变式训练，师生共同分析，小组展开讨论.在分析、讨论、总结的过程中，使学生深入理解抛物线的定义与标准方程，了解概念和定理的形成过程．提高了学生的探究能力，促进学生直观想象素养的培养，提高课堂效率．

3 结束语

在高中数学教学中，要加强对学生直观想象素养的培养．通过直观想象，可以将数学概念化抽象于具体，数学习题化繁为简．使原本复杂无从下手的题目能够更快且准确地找到解题思路.

参考文献：

［1］ 林京榕，王长平，郑雪静，陈清华.高中生直观想象素养的测量与评价研究［J］.数学教育学报，2020（4）：7-12.

［2］ 中华人民共和国教育部．普通高中数学课程标准［M］.北京：人民教育出版社，2019.

［3］ 史宁中．学科核心素养的培养与教学：以数学学科核心素养的培養为例［J］．中小学管理，2017（1）：35-37.

［4］ 章建跃．概念教学必须体现概念的形成过程［J］.数学通报，2010（1）：25-29.

［5］ 马志钢.基于直观想象素养下的数学解题教学［J］.中学数学（高中版），2017（17）：9-11.

［责任编辑：李 璟］

收稿日期：2023-11-25

作者简介：冯立坤，从事高中数学教学研究.

基金项目：本文系福建省教育科学“十四五”规划 2021 年度课题“深度学习视域下信息技术融入几何与代数主题的实践研究”的研究成果之一（立项批准号：FJJKZX21-500）