深埋地下洞室围岩应力分析

吴平

（1.安徽建工集团股份有限公司，安徽 合肥 230031；2.绿色建筑与装配式建造安徽省重点实验室，安徽 合肥 230031）

1 引言

废弃的地下洞室开发再利用是国内学者讨论的热点。目前主要将废弃地下洞室进行旅游开发、修建极深地下实验室及地下储气库等方面的再利用探索[1-3]。压气储能（Compressed Air Energy Storage, 简称“CAES”）是一种利用压缩空气作为介质来存储能量和发电的技术[1-2]，用电低谷时利用多余电能将空气压缩存储至地下洞室内，用电高峰时释放高压空气发电，可以调节电力峰谷，使得电力资源更加合理利用。废弃矿井是作为压气储能电站的天然地下储气结构[3]，据估计，若能利用全国已退的30%废弃矿井建设压气储能站，储能总装机容量相当于三峡电站的总装机容[4]。因此，利用我国地下丰富的废弃矿井建设压气储能电站，对我国能源矿产的再利用和可持续发展具有重要的意义。

废弃地下洞室作为压气储能地下构筑物的关键性能指标是地下洞室围岩的稳定性和密封性[5]，在压气储能电站初期选型时如何快速计算和评价洞室稳定性是目前面临的难题。同时，运营过程中，洞室会经历不断地充气、抽气，如何计算不同充气压下洞室稳定性更加重要。目前国内外众多学者主要采用数值方法对压气储能电站围岩稳定性进行分析，取得了一定的成果[5-9]。如王帅等[7]利用FLAC3D 软件数值分析了内压为10.8MPa 作用下新集三矿地下洞室支护前后的安全稳定性，提出了用于选取合适储气压力的稳定性评价准则；夏才初等[9]采用ABAQUS 有限元软件分析了高内压作用下三种不同截面形式洞室处于不同埋深时洞室围岩应变变化规律；Zimmels 等[10]利用FLAC3D 软件分析了内压作用下单洞室和多洞室的稳定性。解析法有利于探明问题的本质，便于快速计算洞室稳定性，也可有效检验数值模拟的结果，但推导困难，目前研究成果相对较少[5-6]，且洞室截面形状主要为圆形。总体来说，目前还缺乏计算任意形状洞室围岩应力的解析解；鉴于此，本文以孔洞应力近似解析解[18]为基础，提出了一种求解任意截面形式废弃地下洞室围岩应力的计算方法，并以某拟建压气储能示范电站为例，分析了废弃地下洞室的应力场和稳定性，为压气储能电站的选址工作提供基础数据。

拟计划修建一个装机规模10 MW的废弃地下洞室压缩储能示范电站，储气库容积15 万m3，洞内最大气压为10 MPa，洞室所处区域围岩为II 级花岗岩，初始地应力场为自重应力场，不考虑地下水影响，废弃矿井埋深200～600m。为确保拟建地下洞室围岩稳定安全性，需对高内压作用下的洞室围岩应力和稳定性进行分析。在典型的洞室埋深（200m、400m 和600m）下，取马蹄形和圆角方形两种洞室截面形式，考虑不同的洞室尺寸，应用所提出的孔洞应力近似解析解方法，计算不同内压作用下围岩的应力场和塑性区，通过对比分析，确定适合该工程的洞室截面形式、埋深和尺寸，为保证工程的安全实施提供理论基础。

2 深埋洞室围岩应力近似解析解

2.1 集中力作用下半平面应力解析解

根据弹性理论中的表面受集中力作用下半平面应力解析解[17]，如图1 所示，半平面内任意一点的应力可以表示为：

图1 集中力作用下任意倾斜表面的半平面

2.2 分布力作用下半平面应力近似解析解

表面受分布力作用半平面，可采用数值积分法求解半平面任意一点的应力。本文选择高斯积分方法[18]，将分布力作用区域划分若干段，每段含若干高斯点，则分布力可由区域内高斯点处的等效集中力代替。

如图2 所示，半平面表面受分布力pk,n(S)和pk,t(S)作用，则分布面力的水平和竖直分量可表示为：

图2 受分布力作用的半平面

将分布力作用区域ab划分为nk段，每段含w个高斯点，则分布力作用区域内共有mk(=w·nk)个高斯点，位于第j分段的第i个高斯点对应的位置可表示为：

式中，dj为此高斯点所处第j分段的长度，ζi为第i个高斯点对应的系数。

根据高斯积分，位于第j分段的第i个高斯点处等效集中力可表示为：

式中，gk,i=cidj；ci为此高斯点对应的系数。

则分布力作用区域内所有高斯点处的等效集中力可以表示为：

应用叠加原理，分布力或等效集中力作用下半平面内任意一点的应力可表示为：

2.3 表面受等效集中力作用下面内任意线段上等效集中力

则该线段上所有高斯点上的等效集中力为：

式中，Auk=Gu·Uuk，Uuk=

如图3 所示，无限平面内含一个孔边受荷载作用n边孔洞，其应力可用Zhu和Wu[17]提出的方法求解。无限平面内含n边孔洞的应力域可沿其孔边及其延伸边划分为n个半平面应力域；以第n半平面为例，其左延伸边为S2i-1，对应孔边为Sb,i，右延伸边为S2i。将延伸边Si=(i=1,2,...,2n)上分布力转化为等效集中力Qi以及孔边Sb,i=(i= 1,2,...,n)上分布力转化为等效集中力Pi。

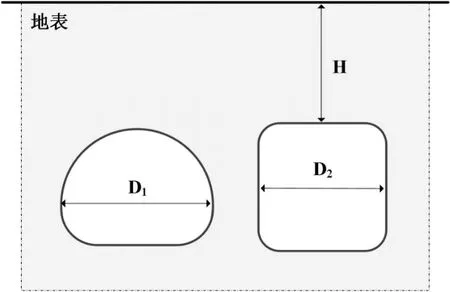
图3 无限平面含凸多边形孔洞

考虑第i半平面，其左右延伸边上等效集中力为Q2i-1和Q2i，对应孔边上等效集中力为Pi，如图3所示，第i+ 1半平面的左延伸边S2i+1位于第i半平面内，该延伸边上等效集中力Q2i+1可用式（9）表示为：

根据延伸边的对应关系，建立延伸边上等效集中力之间的关系表达式：

由式（10）可知，孔边上等效集中力P已知，延伸边上等效集中力Q是未知的，可通过迭代的方法确定Q的准确值。假设等效集中力Q为零，代入式（10）右侧得到Q的第一次修改值，再将其代入式（10）得到第二次修改值，依次计算，直到前后两次迭代过程中Q的最大差值在设定的收敛条件内迭代停止，得到Q的收敛值。对于孔洞外任意一点，确定其所对应的半平面，可用式（6）计算出该点的应力值。

3 用于压气储能的地下洞室

3.1 洞室方案

压气储能洞室由1 条或多条并行洞室构成，拟选择截面积相等的马蹄形截面和圆角方形截面，如图4 所示，马蹄形截面宽度D1取7m、12m 和18m，圆角方形截面宽度D2取5.5m、9m 和13.5m，洞室埋深H取200m、400m 和600m，暂不考虑洞室间相互影响。

图4 废弃矿井压气储能洞室断面示意

3.2 屈服准则和参数选取

围岩为II 级花岗岩，假定为理想弹塑性材料，采用Mohr-Column 屈服准则[19]，利用大、小主应力计算等效应力σe：

式中，c和φ分别为围岩的粘聚力和内摩擦角；σ1和σ3分别为大、小主应力。若等效应力σe>0，应用应力近似解析解可以近似地预测围岩的初始塑性区。由式（11）可知，一点的正等效应力越大，越早发生破坏。

参照行业规范《公路隧道设计规范》（JTG 3370-2018）[20]相关规定，并结合工程经验取值，围岩为II 级花岗岩，其物理力学参数取值见表1所示。

表1 围岩物理力学参数

洞室埋深较深，应力分析时将其看作为无限平面含单孔洞问题。洞室开挖时仅考虑初始地应力，由竖向重力场和水平构造应力构成。开挖后洞室内施加10MPa 内压，获得充气后围岩应力场和塑性区。

4 计算结果及讨论

4.1 马蹄形截面洞室

4.1.1 开挖后洞室应力场和稳定性分析不同埋深下，开挖后相同跨度马蹄形洞室围岩应力分布规律基本一致，跨度为7m 洞室开挖后围岩应力状态如图5 所示。以跨度为7m 洞室为例，开挖后洞室顶部和底部大主应力小，两侧应力大；随着埋深增加，最大主应力数值随之增大。由图5 可知，相同跨度马蹄形洞室随埋深增加，洞室周围塑性区域逐渐增加，这与文献[4]中结果一致。

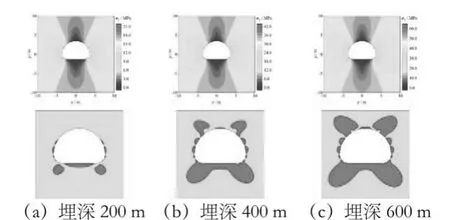
图5 跨度7m的马蹄形洞室应力分布和开挖后塑性区

相同埋深时，不同跨度马蹄形洞室开挖后围岩应力分布基本一致，如图6所示。以埋深为400 m的马蹄形洞室为例，开挖后洞室的顶部和底部应力小、两侧应力大。此外，埋深相同跨度不同的马蹄形洞室开挖后塑性区发展程度基本一致，塑性区与洞室截面积之比基本相同。

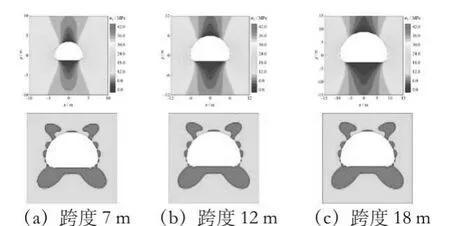
图6 埋深400m的马蹄形洞室应力分布和开挖后塑性区

4.1.2 充气后洞室应力场和稳定性分析

在工作最大气压10MPa 作用下，不同埋深、不同跨度马蹄形洞室围岩应力分布如图7～图9 所示。由图可见，与开挖后未充气洞室比，满充压状态下洞室截面尺寸对洞室围岩应力分布影响小，而埋深对其影响显著。

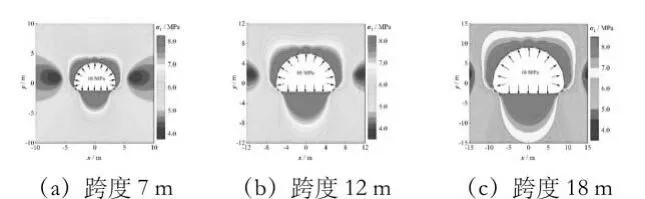
图7 埋深200m不同跨度的马蹄形洞室充气后应力分布

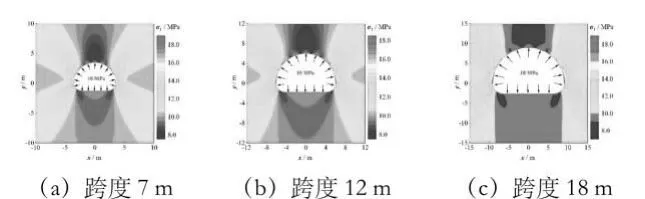
图8 埋深400m不同跨度的马蹄形洞室充气后应力分布

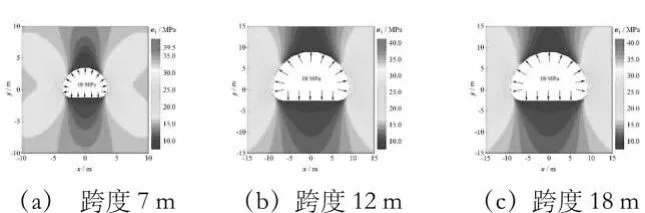
图9 埋深600m不同跨度的马蹄形洞室充气后应力分布

4.2 圆角方形截面洞室

4.2.1 开挖后洞室应力场和稳定性分析

不同埋深下相同跨度圆角方形洞室开挖后的围岩应力分布基本一致，差别主要在于洞周应力值大小，跨度为9m的圆角方形洞室开挖后围岩应力分布和塑性区如图10 所示。由图可见，圆角方形洞室的顶部和底部应力小、侧壁应力大，四个角附近出现应力集中，且应力集中程度随着埋深增加而增大。

图10 跨度9m的圆角方形洞室应力分布和塑性区

以埋深400m 洞室为例，不同跨度圆角方形洞室的应力分布如图11 所示，不同跨度相同埋深的圆角方形洞室开挖后的围岩应力分布形态也基本一致。开挖后洞室顶部和底部的大主应力小、侧壁应力大，角点处出现应力集中。由图11 可知，不同跨度的圆角方形洞室开挖后塑性区形态基本相同，即同一埋深范围内改变洞室截面尺寸对开挖后洞室的塑性区范围影响较小。

4.2.2 充气后洞室应力场和稳定性分析

最大充气压（10MPa）下不同埋深圆角方形洞室的围岩应力分布如图12～图14 所示。由图可见，洞室跨度对充压下圆角方形洞室围岩应力分布形态影响小，但埋深对相同跨度圆角方形洞室的应力分布影响很大。当埋深200m 时，洞周四周（洞顶、洞底和侧壁）的大主应力几乎等于内压（图12）；埋深增大至400m 时，洞室四个角点附近应力最小，而侧壁应力最大（图13）；埋深增大至600m 时，洞室底部和顶部应力最小，侧壁应力最大，角点处无应力集中（图14）。

图12 埋深200m不同跨度的圆角方形洞室充气后应力分布

图13 埋深400m不同跨度的圆角方形洞室充气后应力分布

图14 埋深600m不同跨度的圆角方形洞室充气后应力分布

埋深200m、400m 和600m 时圆角方形洞室的塑性区分布分别如图15～图17 所示。由图可见，相同埋深时，改变洞室跨度对充气引起的塑性区范围影响很小，即塑性区面积与洞室截面积比值不随跨度变化而变化。同一跨度时，塑性区的范围随埋深的增加而减小，且主要出现在洞室顶部和底部附近区域。

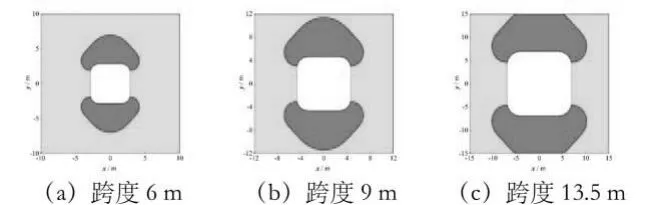
图15 埋深200m不同跨度的圆角方形洞室充气后的塑性区

图16 埋深400m不同跨度的圆角方形洞室充气后的塑性区

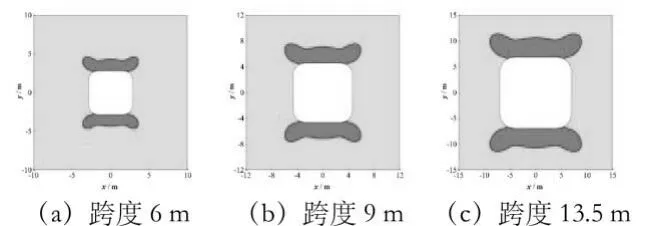
图17 埋深600m不同跨度的圆角方形洞室充气后的塑性区

5 结论

本文提出的深埋洞室围岩应力近似解析解适用于不规则截面废弃地下洞室围岩应力计算和稳定性评价，计算方法和过程简单。

最大充气压下影响洞室稳定性以埋深为主，其中埋深200m 时充气后洞室围岩塑性区最大；400m 和600m 埋深时洞室围岩塑性区发展程度接近；相同洞形情况下，不同充气压下洞室围岩塑性区范围随压力增大而增大。

埋深为400m 的圆角方形洞室稳定性相对较好，适合作为废弃压气储能地下构筑物；各洞室整体稳定性良好，在一定的加固支护措施下具有一定可行性。