涡轮增压器压气叶轮爆裂转速数值分析与试验研究

2020-05-25王文鼎陈世凡

工程设计学报 2020年2期

王文鼎，周东,2，陈世凡,2，刘扬，袁源

（1.重庆江增船舶重工有限公司，重庆402284；2.船舶与海洋工程动力系统国家工程实验室——增压器实验室，重庆402284）

涡轮增压器是内燃机的核心部件［1-2］，随着内燃机不断向高效率、大功率、智能化方向发展，涡轮增压器逐渐向高压比、高转速、大流量方向迈进。由于涡轮增压器压气叶轮转速非常高，若压气叶轮爆裂而引发非包容性事故，将会对内燃机运行安全及人身安全造成极大的危害［3-4］，因此，研究涡轮增压器压气叶轮的爆裂转速和包容性对保障涡轮增压器长期安全运行至关重要。

传统涡轮增压器压气叶轮的材料为高温铸造铝合金，其延展性较差（为3%～5%），目前新型的高强度铝合金具有较好的延展性［5］，可达10%，虽然高温铸造铝合金延性较低，但在破坏之前仍会累积大量的塑性变形。许多学者对旋转机械叶轮的强度进行了理论计算与分析［6-8］，但大多数学者仅考虑材料的线弹性行为，未考虑材料的弹塑性行为，基于线弹性材料模型计算得到的最大von-Mises等效应力偏大，使得叶轮强度校核结果偏保守，从而导致材料的性能无法完全发挥出来［9］。若对旋转机械叶轮进行弹塑性分析，则可精确描述材料应力水平超过屈服强度以后的应力—应变关系，可为材料性能发挥至极限提供合理的依据［2］。

1 压气叶轮爆裂转速计算理论

涡轮增压器压气叶轮受力情况较为复杂，主要受高速旋转产生的离心力的作用。由于压气叶轮与气体摩擦产生的热量较小，则压气叶轮的温升以及气动力较小，因此不考虑温升与气动力的影响［10］。同样，由于压气叶轮轴向尺寸比径向小，不考虑叶片产生的弯曲载荷。此外，压气叶轮为典型的空间轴对称结构，则作用在压气叶轮上的离心载荷和约束也是轴对称的。

1.1 压气叶轮爆裂转速有限元计算理论

在实际工程中，常用有限元法求解压气叶轮在离心载荷作用下的应力［11］。运用有限元法求解压气叶轮应力时，先以压气叶轮有限元模型中各单元的节点位移为基本未知量，引入插值函数对单元进行力学分析，建立其节点力与节点位移的关系；然后通过节点平衡，建立整个有限元模型内所有单元的节点力与节点位移的关系；最后通过求解线性代数方程组，得到压气叶轮应力分析结果。

压气叶轮有限元模型中某三角形单元e的应变分量为：

式中：εx、εr、εθ分别为x、r、θ三个方向（x为轴向，r为径向，θ为周向）的应变；γxr为剪应变；u、v为单元e的变形量。

式（1）可简化为：

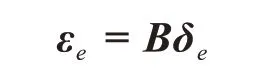
其中：

则单元e的应力分量为：

式中：σx、σr、σθ分别为x、r、θ三个方向的应力；τxr为剪应力；E为弹性模量；μ为泊松比。

根据弹性力学中应力与应变关系［11］，可得：

式中：D为与材料相关的弹性矩阵。

单元e的节点力等于单元刚度矩阵与节点位移的乘积，即“胡克定律”，表示为：

式中：Fe为单元e的节点力矩阵；k为单元刚度矩阵。

整个压气叶轮有限元模型由n个单元构成，基于单元e的节点力与节点位移的关系，建立整个压气叶轮有限元模型内所有单元的节点力与节点位移的关系：

压气叶轮高速旋转时，所受的外力为径向离心力。当压气叶轮的角速度为ω，半径为R，材料密度为ρ时，单元e的单位体积离心力为：

式中：Px、Pr分别为轴向、径向离心力。

压气叶轮匀速转动时处处保持平衡，即任意单元的内力和外力均满足平衡条件：Fe=Pe，则整个压气叶轮有限元模型中所有单元的力平衡方程为：

联立式（1）至（4），求解出压气叶轮有限元模型中某单元的应力，之后通过单元形函数插值法［9］求得整个压气叶轮有限元模型中所有单元的应力。

1.2 压气叶轮爆裂转速的弹塑性分析准则

1）屈服准则选取。

基于von-Mises屈服准则，比较计算得到的压气叶轮最大von-Mises 等效应力σe与材料的屈服强度σy：若σe＜σy，则认为材料处于线弹性阶段；若σe＞σy，则认为材料发生屈服，此时压气叶轮产生局部塑性变形，在离心力作用下塑性变形逐渐扩张，最后导致叶轮破坏［12-14］。

2）破坏准则选取。

压气叶轮轮毂破裂起始于塑性区，引发材料屈服的主要因素是形状改变能密度，无论材料处于何种状态，只要其形状改变能密度达到单向受力屈服时的形状改变能密度，就认为材料屈服，即：在进行有限元计算时，当压气叶轮内任意一点的最大von-Mises等效应力达到材料抗拉强度时即认为叶轮爆裂［15］。

在实际计算中，先采用三维CAD（computer aided design，计算机辅助设计）软件建立压气叶轮几何模型，再用ANSYS Workbench软件设置符合工程实际的边界条件并进行有限元求解，将压气叶轮最大von-Mises等效应力大于材料抗拉强度时的转速看作爆裂转速。为准确模拟压气叶轮爆裂转速，基于线弹性材料模型和双线性等向强化弹塑性材料模型（下文简称为弹塑性材料模型）对压气叶轮的爆裂转速进行分析。

2 压气叶轮有限元模型建立

2.1 压气叶轮材料性能参数

涡轮增压器压气叶轮采用的材料为ZL105A，其性能参数如表1所示。

表1 ZL105A材料性能参数Table 1 Performance parameters of ZL105A material

图1 所示的基于弹塑性材料模型的ZL105A 材料的应力—应变曲线包含弹性斜率和塑性斜率，体现了材料的包辛格效应［11］，说明弹塑性材料模型适用于压气叶轮爆裂转速数值分析。

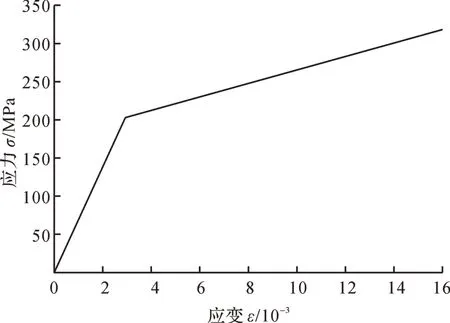
图1 ZL105A材料的应力—应变曲线Fig.1 Stress-strain curve of ZL105A material

2.2 压气叶轮几何模型

采用三维CAD软件建立压气叶轮几何模型。为精确分析压气叶轮的爆裂转速，分别对完整压气叶轮及弱化处理压气叶轮进行模拟。图2（a）所示为完整压气叶轮的几何模型，图2（b）和2（c）分别为弱化处理压气叶轮及其局部放大几何示意图。压气叶轮弱化处理是指通过一定的方法对压气叶轮von-Mise等效应力最大处进行弱化，造成局部应力集中。本文采用的弱化方式为沿叶轮轴孔轴向加工不同深度和不同宽度的预制槽。以往的计算结果表明，压气叶轮最大von-Mises等效应力集中在其轴孔处，在轴孔处开槽并控制开槽的尺寸（槽宽、槽深）即可实现压气叶轮在不同转速下爆裂。

图2 压气叶轮几何模型及几何示意图Fig.2 Geometric model and geometric diagram of compressor impeller

2.3 压气叶轮有限元模型及边界条件

将采用三维CAD软件建立的压气叶轮几何模型导入ANSYS Workbench，选用Solid187 高阶单元进行网格划分，压气叶轮有限元模型如图3所示，其边界条件为叶轮端面轴向约束、径向自由［16-17］，整个叶轮施加转速，边界条件设置如图4所示。

图3 压气叶轮有限元模型Fig.3 Finite element model of compressor impeller

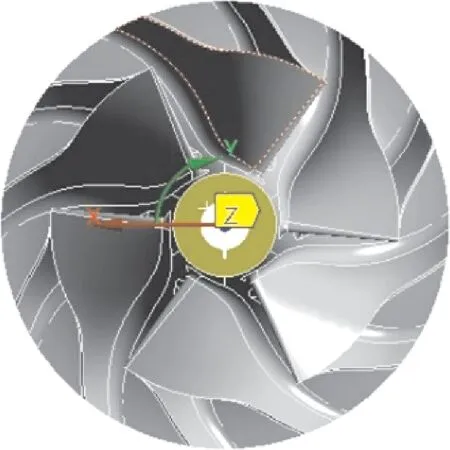
图4 压气叶轮有限元模型边界条件设置Fig.4 Boundary condition setting of compressor impeller finite element model

3 压气叶轮爆裂转速及应力的数值分析

3.1 基于线弹性材料模型的完整压气叶轮爆裂转速

基于线弹性材料模型，对完整压气叶轮进行数值分析，得到其von-Mises等效应力分布云图，如图5所示。有限元结果表明，无论加载多大的转速，完整压气叶轮的最大von-Mises 等效应力均出现在靠近轮背侧的轴孔处，不同转速下完整压气叶轮的最大von-Mises等效应力如表2所示。由表2可知：当转速为156 400 r/min 时，完整压气叶轮的最大von-Mises等效应力为333.51 MPa，大于压气叶轮材料的抗拉强度330 MPa，由此可得运用线弹性材料模型计算得到的完整压气叶轮的爆裂转速为156 400 r/min。

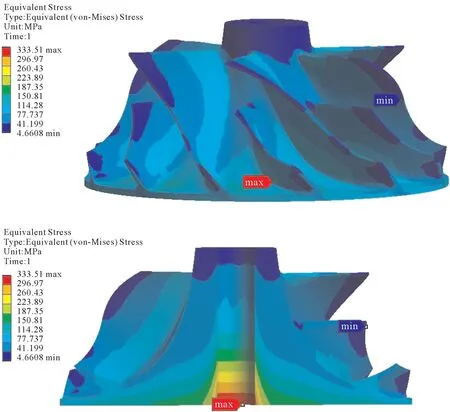
图5 基于线弹性材料模型的完整压气叶轮von-Mises 等效应力分布云图Fig.5 Von-Mises equivalent stress distribution cloud diagram of complete compressor impeller based on linear elastic material model

3.2 基于弹塑性材料模型的完整压气叶轮爆裂转速

基于弹塑性材料模型，对完整压气叶轮进行数值分析，得到其von-Mises等效应力分布云图，如图6所示。加载不同转速时，完整压气叶轮的最大von-Mises 等效应力出现的位置与基于线弹性材料模型的分析结果相同，即最大von-Mises等效应力均出现在靠近轮背侧的轴孔处。

表2 不同转速下完整压气叶轮的最大von-Mises等效应力Table 2 Maximum von-Mises stress of complete compressor impeller under different rotational velocities

图6 基于弹塑性材料模型的完整压气叶轮von-Mises 等效应力分布云图Fig.6 Von-Mises equivalent stress distribution cloud diagram of complete compressor impeller based on elastolplastic material model

当加载转速为182 000 r/min 时，完整压气叶轮的最大von-Mises 等效应力为339.7 MPa，已超过压气叶轮材料的拉伸强度330 MPa，由此可得运用弹塑性材料模型计算得到的完整压气叶轮的爆裂转速为182 000 r/min。

3.3 基于线弹性材料模型的弱化处理压气叶轮爆裂转速

基于线弹性材料模型对弱化处理压气叶轮进行数值分析，表3为不同弱化处理方式所对应的压气叶轮预制槽的具体尺寸，图7所示为2种弱化处理压气叶轮的von-Mises等效应力分布云图。

由图7可知，无论采用弱化处理方式I还是弱化处理方式Ⅱ，压气叶轮的最大von-Mises 等效应力均集中在压气叶轮轴孔开槽处，这验证了在压气叶轮轴孔处开槽可使压气叶轮局部应力集中，从而使压气叶轮爆裂。同时，还可以发现von-Mises等效应力沿压气叶轮径向、轴向急剧衰减。

表3 弱化处理压气叶轮预制槽尺寸Table 3 Size of prefabricated groove of weakened compressor impeller 单位：mm

图7 基于线弹性材料模型的弱化处理压气叶轮von-Mises等效应力分布云图Fig.7 Von-Mises equivalent stress distribution cloud diagram of weakened compressor impeller based on linear elastic material model

基于线弹性材料模型的2种弱化处理压气叶轮的最大von-Mises等效应力如表4所示。

表4 基于线弹性材料模型的弱化处理压气叶轮的最大von-Mises等效应力Table 4 Maximum von-Mises equivalent stress of weakened compressor impeller based on linear elastic material model

3.4 基于弹塑性材料模型的弱化处理压气叶轮爆裂转速

基于弹塑性材料模型，对弱化处理压气叶轮进行数值分析，其von-Mises 等效应力分布云图如图8所示。由图8 可知，弱化处理压气叶轮的最大von-Mises等效应力集中在压气叶轮轴孔开槽处，并沿径向及轴向迅速衰减。对比图7和图8发现，基于线弹性材料模型的弱化处理压气叶轮的von-Mises 等效应力衰减得更为明显。

图8 基于弹塑性材料模型的弱化处理压气叶轮von-Mises等效应力分布云图Fig.8 Von-Mises equivalent stress distribution cloud diagram of weakened compressor impeller based on elastolplastic material model

基于弹塑性材料模型的2种弱化处理压气叶轮的最大von-Mises等效应力如表5所示。

表5 基于弹塑性材料模型的弱化处理压气叶轮的最大von-Mises等效应力Table 5 Maximum von-Mises equivalent stress of weakened compressor impeller based on elastoplastic material model

基于线弹性材料模型和弹塑性材料模型，对4种弱化处理压气叶轮进行数值分析，得到的最大von-Mises等效应力和爆裂转速如图9所示，图中虚线为压气叶轮材料的抗拉强度。

图9 4 种弱化处理压气叶轮的最大von-Mises 等效应力和爆裂转速Fig.9 Maximum von-Mises equivalent stress and bursting rotational velocity of four weakened compressor impellers

从图9中可以发现，采用弱化处理方式I、Ⅱ的压气叶轮的最大von-Mises 等效应力均大于330 MPa，而采用弱化处理方式Ⅲ、Ⅳ的压气叶轮的最大von-Mises等效应力均接近330 MPa，由此可确定压气叶轮的最佳开槽尺寸。同时，还可以发现随着槽深增大，压气叶轮的爆裂转速和最大von-Mises等效应力均增大；随着槽宽减小，压气叶轮的爆裂转速和最大von-Mises等效应力也增大。这表明增大槽深和减小槽宽均能使压气叶轮局部应力集中并爆裂，因此通过控制开槽的尺寸（槽宽、槽深）即可实现压气叶轮在不同转速下爆裂。

3.5 压气叶轮von-Mises等效应力

3.5.1 压气叶轮径向von-Mises等效应力

提取基于弹塑性材料模型的完整压气叶轮、2种弱化处理（I、Ⅱ）压气叶轮的径向von-Mises等效应力，结果如图10所示。

由图10可知，3种压气叶轮的径向von-Mises等效应力均呈减小趋势，轴孔径向2 mm范围内无论有无开槽，压气叶轮的von-Mises等效应力均先快速减小再缓慢减小，最后在出气边尾橼处极速减小。这是因为压气叶轮轴孔及开槽均会引起局部应力集中，而开槽使应力集中更加明显。压气叶轮尾橼处von-Mises 等效应力极速减小是因为尾橼处叶片与轮毂交界处结构存在突变［18］。

3.5.2 压气叶轮轴向von-Mises等效应力

提取基于弹塑性材料模型的完整压气叶轮、2种弱化处理（I、Ⅱ）压气叶轮的轴向von-Mises等效应力，结果如图11所示。

由图11可知，完整压气叶轮轴向von-Mises等效应力呈逐渐减小的趋势，在短叶片处等效应力急速减小，而2 种弱化处理压气叶轮的von-Mises等效应力的变化趋势一致。开槽导致压气叶轮轴向von-Mises等效应力先增大后减小，使得压气叶轮von-Mises等效应力最大的位置发生变化，还使得压气叶轮轴向von-Mises等效应力的衰减速度比完整压气叶轮慢。

图10 压气叶轮径向von-Mises等效应力Fig.10 Radial von-Mises equivalent stress of compressor impeller

图11 压气叶轮轴向von-Mises等效应力Fig.11 Axial von-Mises equivalent stress of compressor impeller

4 压气叶轮爆裂转速试验研究

分别对完整压气叶轮、2 种弱化处理（I、Ⅱ）压气叶轮进行台架试验，试验现场如图12所示。

图12 压气叶轮台架试验现场Fig.12 Compressor impeller bench test site

4.1 完整压气叶轮爆裂状态

图13所示为完整压气叶轮爆裂状态，当转速为185 000 r/min 时，完整压气叶轮爆裂。由图13 可看出，完整压气叶轮在离心力的作用下均匀爆裂成3块，压气叶轮叶片与叶轮罩壳等发生激烈碰撞，致使压气叶轮叶片全部断裂，这与其他学者的研究结果一致［17，19-21］。

图13 完整压气叶轮爆裂状态Fig.13 Bursting state of complete compressor impeller

4.2 弱化处理压气叶轮爆裂状态

图14 所示为2 种弱化处理压气叶轮的爆裂状态。由图14可看出，弱化处理压气叶轮均从开槽处断裂为均匀的两部分，这是因为开槽处较为薄弱，在离心力的作用下易断裂；同时弱化处理压气叶轮的叶片均被撞断。

4.3 压气叶轮爆裂转速计算值与试验值对比

提取完整压气叶轮及弱化处理压气叶轮爆裂转速的计算值和试验值，结果如图15所示。

由图15可知，无论是完整压气叶轮还是弱化处理压气叶轮，基于线弹性材料模型的爆裂转速计算值远小于试验值，基于弹塑性材料模型的爆裂转速计算值接近试验值。

图14 弱化处理压气叶轮爆裂状态Fig.14 Bursting state of weakened compressor impeller

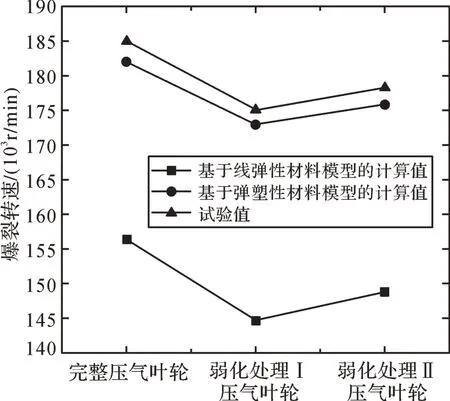
图15 压气叶轮爆裂转速计算值与试验值对比Fig.15 Comparison of calculated values and experimental values of bursting rotational velocity of compressor impeller

为更直观地说明弹塑性材料模型在分析压气叶轮爆裂转速时的准确性，计算基于线弹性材料模型和弹塑性材料模型的压气叶轮爆裂转速计算值与试验值的误差（转速误差1和2）；计算基于弹塑性材料模型的压气叶轮最大von-Mises 等效应力与压气叶轮材料抗拉强度的误差（应力误差1），同时，将爆裂转速试验值代入弹塑性材料模型，计算压气叶轮的最大von-Mises等效应力，并计算它与压气叶轮材料抗拉强度的误差（应力误差2），结果如图16所示。

由图16可知：基于线弹性材料模型的压气叶轮爆裂转速计算值与试验值的误差较大，约为16%；基于弹塑性材料模型的压气叶轮爆裂转速计算值与试验值的误差较小，约为2%；基于弹塑性材料模型的压气叶轮最大von-Mises 等效应力与材料理论抗拉强度的误差约为2%；代入爆裂转速试验值后计算得到最大von-Mises 等效应力与材料理论抗拉强度的误差约为4%，这是因缺乏材料应力与应变试验数据而采用模型进行简化处理所引起的误差。