一种区域降水预测的时空集成模型

马宇红 薛生倩 王小小 路金叶

DOI：10.16783/j.cnki.nwnuz.2024.03.012

收稿日期：2023-12-05;修改稿收到日期：2024-03-12

基金項目：国家自然科学基金资助项目（51368055）

作者简介：马宇红（1971—），男，甘肃天水人，副编审，博士.主要研究方向为时空序列数据建模和预测.

E-mail：mayh@nwnu.edu.cn

摘要：提出了一种融合多种深度学习方法的时空预测集成模型LSTM-ARIMA-SARIMA-BP-CNN（简称LASBC模型），其中ARIMA模型捕捉降水时间序列的近邻性，SARIMA模型捕捉周期性，BP神经网络揭示降水分布的时空相关性，CNN挖掘气象、地理因素对降水的影响，最后通过LSTM网络对4个模型的预测结果进行融合，提高预测精度.以中国西部地区12个城市1985年1月至2021年12月的月降水量数据为主，应用LASBC模型对12个城市的月降水量进行预测，结果显示：LASBC模型的预测精度显著提高；基于预测月降水量，给出了6个主要城市未来10年气候偏干旱或湿润的月份及降水量；未来10年，我国西北干旱区年均降水基本保持稳定，高寒冻土区略有增加，西南湿润区增长趋势明显.

关键词：降水分布；时空预测；机器学习；集成模型；时空相关性

中图分类号：TP 391.42;R 742.5    文献标志码：A    文章编号：1001-988Ⅹ（2024）03-0105-10

A spatiotemporal integrated model for

regional precipitation prediction

MA Yu-hong1，2，XUE Sheng-qian1，WANG Xiao-xiao1，LU Jin-ye1

（1.College of Mathematics and Statistics，Northwest Normal University，Lanzhou 730070，Gansu，China;

2.Editorial Department of the University Journal，Northwest Normal University，Lanzhou 730070，Gansu，China）

Abstract：A spatiotemporal prediction model LSTM-ARIMA-SARIMA-BP-CNN（LASBC） for regional precipitation is proposed，which integrates multiple deep learning methods.Among them，ARIMA model captures the time-neighbor correlation of precipitation time series，SARIMA model captures the periodic trend of precipitation time series，BP neural network reveals the spatiotemporal correlation of precipitation distribution，CNN network excavates the influence of meteorological and geographical factors on precipitation，and finally，LSTM network is used to fuses the prediction results of the four models so as to improve the prediction accuracy.Based on the monthly precipitation data of major cities in western China from January 1985 to December 2021，the LASBC model is used to forecast the monthly precipitation of 12 cities in western China.The results show that the prediction accuracy of the LASBC model is greatly improved;the predicting months and precipitations for six major cities with a slightly arid or humid climate in the next 10 years are given

based on  the predicted monthly precipitation;in the next ten years the annual average precipitation in the northwest

arid region has remained stable，with a slight increase in the high-altitude permafrost region and a significant growth trend in the southwest humid region.

Key words：precipitation distribution;spatiotemporal prediction;machine learning;integration model;spatiotemporal correlation

众所周知，一个地区降水量的时空分布严重影响着人们生产生活的各个方面.我国西部地区地域辽阔，地形复杂，属于典型的温带大陆性气候和高原山地气候，降水空间分布极不均匀，局地差异大；降水量按季度、按月度分布很不平衡，冬季干旱少雨，夏季水量充沛.降水的时空不均衡严重影响区域生态环境及经济发展，所以挖掘区域降水数据的时空分布规律，准确预测未来降水的时空分布对于高效利用降水改善生态环境、发展区域经济及预防地质灾害都具有重要的现实意义.

1  研究综述

降水预测模型通常分为5类：物理模型、统计模型、机器学习模型、深度学习模型和集成学习模型，物理模型也称为过程模型，它需要考虑影响降水的各种气象因素，通过模拟降水的物理过程对降水进行预测，统计模型、机器学习模型、深度学习模型和集成学习模型统称为数据驱动模型，它通过挖掘蕴含在降水历史数据中的内在规律和演化趋势对降水的时空分布和强度进行预测.

物理模型根据空气动力学和热力学原理揭示降水过程中各种气象因素对降水分布及强度的影响.2004年，陈菊英等［1］通过集成多种降水前兆敏感因子，建立了海河流域汛期降水的多级预报物理模型；马振锋等［2］根据四川盆地固有的三类降水分布特征，建立了一种预测川渝地区汛期降水量的物理模型.物理模型虽然对降水的物理过程和各种气象因素的影响解释清晰，预测精度高，但物理模型的建立需要大量专业的气象知识，且很容易受到各种突发性随机因素的干扰.

统计模型主要通过对历史降水数据的统计分析建立回归方程进行预测，当前最流行的统计模型是差分自回归移动平均（Auto-Regressive Integrated Moving Average， ARIMA）模型.胡盈等［3］利用江西省 16 个气象站点逐月降水量数据建立 ARIMA 模型，并对 2020—2021 年的逐月降水量进行预测；Coban等［4］基于ARIMA模型对土耳其马尔马拉地区的降水进行预测；Nayagam等［5］通过线性回归模型对印度喀拉拉邦夏季降水进行预测；Huang等［6］提出了一种年际增量结合经验正交分解的统计预测方法；Wang等［7］采用经验正交函数和旋转经验正交函数分析了1960—2010年我国降水的时空分布特征及演化规律.统计模型简单直观，当降水时间序列是线性或接近线性时，统计模型能产生令人满意的预测结果，但当时间序列呈现非线性时预测精度往往差强人意.

机器学习模型通过模拟人脑的工作方式，自动学习和提取降水数据的特征进行预测.机器学习模型具有较强的自适应性和学习能力，能够处理非线性和非平稳的数据，但需要大量的训练数据和计算资源.近来，Chau等［8］结合奇异谱分析（Singular Spectrum Analysis， SSA）和支持向量回歸（Support Vector Regression， SVR）实现了巴基斯坦3类农业带的月降水预测；Hartigan等［9］使用随机森林（Random Forest， RF）和SVR对悉尼流域的降水和气温进行预测；Xiang 等［10］利用决策树（Decision Tree， DT）和RF对重庆市的夏季降水进行预测；Rostam等［11］通过多层感知器探索伊朗首都德黑兰大尺度气候指数与降水之间的联系；Lu等［12］通过具有不同核函数的支持向量机（Support Vector Machine， SVM）预测广西地区的月降水量；Kisi等［13］结合离散小波变换（Discrete Wavelet Transform， DWT）和SVM对土耳其伊兹密尔和阿菲永站的日降水量进行预测.

深度学习模型是神经网络模型的扩展，它通过增加网络深度和宽度处理更为复杂的数据.降水数据通常具有时空依赖性、大规模和高维度属性，深度学习模型不仅适应于大规模数据建模，而且能够自动捕获数据的时空依赖性，所以广泛应用于时空数据建模与预测.典型的深度学习模型有卷积神经网络（Convolutional Neural Network，CNN）、深度置信网络（Deep Belief Networks， DBN）和堆栈自编码网络（Stacked Auto-Encoder Network， SAEN）.Luc等［14］使用多层前馈神经网络（Multi-Layer Feed-forward Network， MLFN）、偏循环神经网络和时间延迟神经网络对悉尼帕拉马塔河流域10次暴雨事件的降水量进行预测；Baratta等［15］结合MLFN和SSA对意大利台伯河流域的日降水量进行预测；Nasseri等［16］将遗传算法与ANN相结合，对悉尼帕拉马塔河流域上游降水进行短期预测；LI等［17］基于BP神经网络对浙江北部夏季降水量进行预测；Shi等［18］提出了一种基于CNN的降水预测方法；Du等［19］成功地将DBN模型应用到天气降水预测研究中；Ha等［20］使用DBN提高了韩国首尔地区降水和温度等的预测精度；Tao等［21］结合Atrous小波变换建立了一个具有注意机制的多尺度长短期记忆（Multiscale Long-Short Term Memory， MLSTM）神经网络，并对长江流域129个监测站月降水量的预报精度进行改进；Misra等［22］提出了基于LSTM的循环神经网络模型，并利用印度马哈纳迪盆地的降水数据和加拿大坎贝尔河流域的降水数据测试了模型的可靠性.

集成学习模型可以对多种预测模型进行融合，如将统计模型和物理模型进行加权融合，或对多个深度学习模型集成优化.多模式集成预测是一种信息后处理技术，它通过综合不同方面的信息或各有所长的建模方法有效改善模型的预测精度.近来，Wu等［23］建立了一种混和深度学习模型预测具有时空依赖的区域O3和NO2的浓度；Ding等［24］结合时空建模和多尺度网络预测城市出租车的需求；Yu等［25］建立了基于集成深度图注意强化学习网络的多因素驱动时空风电预测模型.

受集成学习方法的启发，本文根据降水数据的高度时空依赖性和外在气象因素的强关联性，首先通过ARIMA模型、季节性ARIMA模型（SARIMA）、BP神经网络和CNN分别对某区域的降水进行预测，然后再通过LSTM 对4种模型的预测结果进行融合，建立了一种深度学习集成预测模型LSTM-ARIMA-SARIMA-BP-CNN（简称LASBC模型），其中 ARIMA模型和SARIMA模型分别捕捉降水的时间近邻性和周期性，BP神经网络模型挖掘降水数据的时空相关性，CNN模型揭示外在的气象和地理因素对降水的影响.以中国西部地区12个城市1985年1月至2021年12月的月降水量数据为主，结合当月平均温度、相对湿度、日照时数等气象因素以及经度、纬度、海拔高度等地理数据，应用LASBC模型对西部12个主要城市的月降水量进行预测，结果显示：与4个单一预测模型相比，新模型的预测精度大幅提高；基于预测月降水量，给出了6个主要城市未来10年气候偏干旱或湿润的月份及相应的降水量；分析每5年的年均降水量可知，未来10年我国西北干旱区降水量基本稳定，高寒冻土区略有增加，西南湿润区增长明显.

2  模型与方法

2.1  时空序列模式

2.1.1  时间的近邻性和周期性  一般而言，事物的发展变化在时间上具有近邻相关性，时间越接近状态越相似，时间近邻预测就是用时间序列连续的前n个值去预测当前值；时间序列的周期性刻画了事物发展的周期性变化，如月亮的圆缺和河水潮汐的变化明显以月为周期，所以第t天的变化不仅与前n天的变化密切相关，而且与其上个月、上上个月相邻日期的变化高度相似.

时空序列的时间近邻模式和周期模式可以表述為

TCs，t～（xs，t-n，xs，t-（n-1），…，xs，t-2，xs，t-1），

TPs，t～（xs，t-n·T，xs，t-（n-1）·T，…，xs，t-2·T，xs，t-1·T），

其中s为数据监测点，t为当前时刻，n是历史时间滞后期，即用监测站s前n个时刻的值预测当前时刻的值，T是时间序列的周期；TC代表时间近邻模式，TP代表时间周期模式.所以时间近邻预测和时间周期预测分别表达为

TCs，t=fTCs（xs，t-n，xs，t-（n-1），…，xs，t-2，xs，t-1），

TPs，t=fTPs（xs，t-n·T，xs，t-（n-1）·T，…，

xs，t-2·T，xs，t-1·T）.

2.1.2  时空的近邻性  根据地理学第一定律，任何地理事物在时间和空间上都是高度依赖的，时间越接近状态越相似，空间越接近属性越相似.时空预测就是用事物所有近邻前n个时刻的状态或属性去推断其当前的状态或属性.以B（s，r）表示以s为中心、r为半径的邻域，记

Γs={1≤i≤S：i∈B（s，r）}={s1，s2，…，sk}

为监测点s在其r邻域内所有近邻点的集合，因为监测点s在t时刻的预测值STs，t与其所有k个近邻前n个时刻的值相关，所以对空序列的时空相关模式可以表述为

STs，t～（xs1，t-n，xs1，t-（n-1），…，xs1，t-1，…，

xsk，t-n，xsk，t-（n-1），…，xsk，t-1），

其中si（1≤i≤k）为监测点s的第i个近邻，ST代表时空近邻模式.所以时空近邻预测表达为

STs，t=fSTs（xs1，t-n，xs1，t-（n-1），…，xs1，t-1，…，

xsk，t-n，xsk，t-（n-1），…，xsk，t-1）.

2.1.3  外在因素相关性  任何事物都不是孤立存在的，其发展变化必然受环境因素的影响，当前状态或属性与许多特定因素具有很强的相关性，如一地某时刻的空气质量不仅受到该地前n个时刻风速、风向、温度、湿度等气象因素的影响，也受到地形及人类活动的影响.所以外在因素相关性模式可以表述为

FCs，t～（y1s，t-n，y1s，t-（n-1），…，y1s，t-1…，

yms，t-n，yms，t-（n-1），…，yms，t-1），

其中FC代表因素相关，m代表相关因子数，n代表时间滞后期.所以外在因素相关的预测可以表述为

FCs，t=fFCs（y1s，t-n，y1s，t-（n-1），…，y1s，t-1…，

yms，t-n，yms，t-（n-1），…，yms，t-1）.

2.2  基础模型

2.2.1  ARIMA和SARIMA模型  ARIMA模型是20世纪70年代Box和Jenkins提出的一种时间序列预测方法［26］.在ARIMA（p，d，q）模型中，AR为自回归项，MA为滑动平均项；p为自回归阶数，q为滑动平均阶数，d为使时间序列成为平稳序列所做的差分次数（阶数）.一般地，d=0的ARIMA（p，d，q）模型表示为

t=c+∑pi=1φiXt-i+∑qj=1θjεt-j+εt，

其中φi（1≤i≤p）和θj（1≤j≤q）为不全为零的待定系数；εt为独立的误差项；Xt为平稳、正态、零均值的时间序列.ARIMA模型简单，但缺点是要求时间序列数据是平稳的或者差分后是平稳的，并且其只能捕捉时间序列数据的线性关系而不能捕捉非线性关系.SARIMA模型主要处理具有明显周期性的时间序列.如果时间序列数据是一个非平稳时间序列，并且在大尺度上存在明显的周期性，则需要先对时间序列进行周期差分，然后再进行若干次趋势差分，使之成为平稳时间序列然后才能应用ARIMA模型.

平稳时间序列的均值和协方差不随时间变化，数据序列的平稳性一般使用ADF检验和KPSS检验来判断.ADF检验是一种基于单位根检验的平稳性检验方法，如果ADF统计量小于对应的临界值，且P值小于显著性水平，则认为时间序列是平稳的；KPSS检验与ADF检验相反，它假设时间序列是平稳的，然后通过KPSS统计量来检验这个假设，如果KPSS统计量小于对应的临界值，且P值小于显著性水平，则时间序列是平稳的.

2.2.2  BP神经网络  BP（Back Propagation）神经网络是1986年Mcclleland等［27］建立的一种按照误差逆向传播算法训练的多层前馈神经网络，它的基本思想是利用梯度下降法使网络的实际输出值和期望输出值之间的均方误差最小.BP神经网络在输入层与输出层之间增加了若干隐含层神经元，神经元状态的改变影响输入与输出之间的关系.BP神经网络由正向计算过程和反向计算过程组成，正向传播过程从输入层经过隐含层逐层处理，并转向输出层，每一层神经元的状态只影响下一层神经元的状态；如果输出层不能得到预期输出，则将误差沿原路反向传播，通过修改各神经元的权值使得输出误差最小.

2.2.3  卷积神经网络（CNN）  CNN是一类包含卷积操作且具有深度结构的前馈神经网络，其研究始于20世纪80～90年代，时间延迟网络和LeNet-5是最早出现的卷积神经网络［28］.CNN既具有良好的特征提取能力，又具有较强的辨别能力，因此在机器学习系统中主要用于特征提取和分类.经典的CNN结构由卷积层和池化层交替叠加组成，最后由全连接层输出.首先，数据在卷积层和若干个卷积核进行卷积操作，提取输入特征；然后，池化层对卷积层提取的特征进行选择，池化操作有助于特征的组合；最后，全连接层进行拟合，减少特征信息的损失.

2.3.4  长短期记忆网络（LSTM）  LSTM网络是一种具有独特三门结构的循环神经网络［29］，遗忘门决定网络对上一层输入的保留程度，输入门决定网络对新输入的保留程度，输出门决定网络对输出的保留程度.LSTM的这种门结构不仅可以控制信息流的走向，而且可以防止循环神经网络长时间依赖上的梯度消失或梯度爆炸现象，特别适合处理间隔较长的时间序列.

2.3  集成模型结构

一个地区所在的海陆位置、地形、气压、风

带、洋流、太阳黑子以及人类活动对降水均有很大影响，所以降水序列数据具有特殊的时空结构特征.为了综合考虑影响降水的各种气象因素及地理因素，并充分发掘蕴含在历史降水数据中的内在规律，提高降水预测精度，本文建立一个多模型集成学习预测模型LASBC，其中ARIMA模型捕捉降水时间序列的近邻性特证，SARIMA模型捕捉周期性特征，BP神经网络模型挖掘时空相关性，CNN揭示气象和地理因素在时间和空间维度上对降水的影响，最后，4个子模型的预测结果再由LSTM模型进行融合，得到更高精度的预测结果.

LASBC集成学习模型的基本思想为

s，t=fs（TCs，t，TPs，t，STs，t，FCs，t），

其中TCs，t，TPs，t，STs，t，FCs，t分别是ARIMA、SARIMA、CP和CNN 模型的预测结果，集成学习模型的整体流程与结构如图1所示.

2.4  性能评估指标

使用平均绝对误差（MAE）、均方误差（MSE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE）4个指标对模型的预测性能进行评价，其定义分别为

MAE=1n∑ni=1｜i-xi｜，

MSE=1n∑ni=1（i-xi）2，

RMSE=1n∑ni=1（i-xi）2，

MAPE=1n∑ni=1｜（i-xi）/xi｜·100%，

其中，n为数据的个数，xi表示第i个数据的真实值，i表示所有第i个数据的预测值.评价指标的值越接近于0，模型预测精度越高.

3  应用分析

3.1  数据集介绍

我国西部地区属于典型的温带大陆性气候和高原山地气候，在气候上可以分为高寒冻土区、西北干旱区和西南湿润区3個区域，降水在时间分布上具有明显季节性，夏季降水丰沛，冬季降水稀少；降水量空间分布极为不均，总体表现为从东南向西北逐步减少.西部地区地域广阔、城市众多，我们选取气象、地理数据及降水监测数据相对完整的12个省会城市西安、银川、兰州、西宁、乌鲁木齐、成都、重庆、拉萨、昆明、贵阳、南宁、呼和浩特作为研究对象，数据集为12个城市1985年1月到2021年12月共37年的月降水量数据，以及每月的平均温度、相对湿度、日照时数等气象数据和城市经度、纬度、海拔高度等地理数据，数据整理自《中国气象统计年鉴》（1985—2021）及中国气象网.

为了直观展示各模型的预测精度，我们选取高寒冻土区的拉萨和西宁、西北干旱区的乌鲁木齐和西安、西南湿润区的重庆和南宁6个主要城市进行对比，以1985年1月至2016年12月的数据为训练集，2017年1月至2021年12月的数据为测试集，并对2022年1月至2031年12月各城市的降水进行前瞻性预测.

3.2  模型参数设置

6个主要城市：拉萨、西宁、乌鲁木齐、西安、重庆、南宁的降水量数据先做一次周期差分，再做一次趋势差分后经检验成为平稳时间序列，最后通过AIC和BIC准则确定最优的自回归阶数p和滑动平均阶数q，得到6个城市对应的ARIMA模型分别为ARIMA（2，1，4），ARIMA（3，1，4），ARIMA（3，1，2），ARIMA（4，1，4），ARIMA（4，1，4）和ARIMA（3，1，2）.BP神经网络为4层结构，输入层4个神经元（时间滞后期n=4），第一隐层30个神经元，第二隐层10个神经元，输出层1个神经元；训练函数选择traingd梯度下降法，最大训练次数为4000，学习率为0.02，训练精度10-5.CNN网络为LeNet-5架构，不同城市近邻数可能有所不同，但时间滞后期统一设置为3，若城市的近邻数为m，则输入特征为3m，使用adam优化器，设置最小批处理数为16，梯度阈值为1，初始学习率为0.05，迭代次数为250.LSTM的输入层特征维度为4，隐含单元数为100，输出全连接层特征维度为1，使用adam优化器，最大训练轮数为250，梯度阈值为1，初始学习率为0.005.

3.3  结果与分析

图2是6个主要城市测试集的预测结果，其中红线代表预测值，蓝线代表真实值.由图2可知，6个主要城市的降水量在时间上具有明显的周期性，每年丰水期、枯水期特征分明，水量差别大.表1为LASBC模型和SARIMA模型、ARIMA模型、BP模型、CNN模型对6个主要城市降水预测性能的评价指标.结合图2和表1可知，LASBC模型对6个城市降水量的预测与实际降水量最为接近，误差最小.以经典的RMSE为例，拉萨的RMSE为10.72，比单纯的SARIMA模型、ARIMA模型、BP模型和CNN模型分别改进了73.4%，62.2%，70.7%和42.9%，平均改进率62.3%；西安的RMSE为15.75，比单纯的SARIMA模型、ARIMA模型、BP模型和CNN模型分别改进了55.6%，58.8%，64.9%和49.4%，平均改进率57.2%；LASBC模型对乌鲁木齐、拉萨、西宁和西安的预测精度最高，RMSE分别为7.63，10.72，11.21和15.75，而对重庆和南宁的预测精度较低，RMSE分别为46.35和46.57，原因是：一方面，重庆和南宁地处西南湿润区，月降水量的绝对数值大导致误差偏大；另一方面，西南湿润区受拉尼娜和厄尔尼诺气候影响明显，降水分布随机性强、强度波动性大导致误差偏大.综合评价可知，本文模型预测精度更高，性能更好.

3.4  未来预测

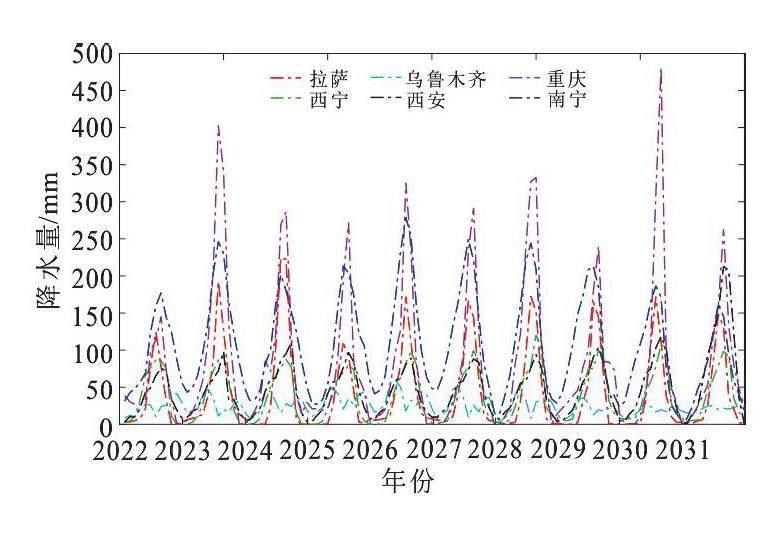
为了探究中国西部地区未来10年降水量的变化，我们应用LASBC模型对西部地区6个主要城市：拉萨、西宁、乌鲁木齐、西安、重庆、南宁2022年1月至2031年12月共10年的降水分布及强度进行前瞻性预测，结果见图3.由图3可以看出，整个西部地区未来10年的月降水量及分布与前40年相比变化不大，夏季降水集中，水量充沛，冬季降水稀少；西南湿润区的重庆和南宁，夏季降水量明显高于西北干旱区的乌鲁木齐和西安，其中南宁市2023年8月降水量会突破400 mm，2031年8月降水量更是接近500 mm；乌鲁木齐和西宁全年降水稀少，乌鲁木齐最高月降水量不会超过100 mm，西宁更是在50 mm附近徘徊，但乌鲁木齐和西宁市夏季和冬季降水量差异最少，原因可能是冬季降雪补偿引起的.

图4是拉萨、西宁、乌鲁木齐、西安、重庆、南宁6个主要城市1991年1月至2031年12月每5年平均年降水量变化趋势.从图4可以看到，高寒冻土区的拉萨和西宁未来10年内降水量略有增加，2021—2025年年均降水量为479.74 mm和423.79 mm，2026—2030年年均降水量为502.16 mm和470.16 mm，相比上个5年降水分别增加22.42 mm和46.37 mm；西北干旱区的乌鲁木齐和西安的降水量有波动，但变化不大，乌鲁木齐和西安市2021—2025年的年均降水量分别为423.79和303.27 mm，而2026—2030年的年均降水量为470.16和292.73 mm，乌鲁木齐略有增加，而西安则略有减少；西南湿润区的重庆的降水量在1996年后持续增加，至2016年后年降水量已经超过1 000 mm，预测未来降水量总体会波动增加，南宁市年均降水量多年保持在1 200～1 400 mm之间，虽然偶尔有所波动，但总体保持平稳，变化不大.

总体来说，中国西部地区近40年降水量呈现缓慢增加的趋势，高寒冻土区与西北干旱区增长缓慢，而西南湿润区降水呈现较明显的增长趋势.未来10年，中国西部地区的年平均降水量总体不会有明显增加的趋势.

表2是模型预测得到的我国西部6个城市未来10年内偏干旱和湿润的月份及降水量，降水分布的巨大差异对西部地区的工农业生产、生态保护和防灾减灾工作都提出了新的挑战，针对降水稀少和丰沛的月份，各地政府部门可提前做好水资源调配利用和防旱防涝准备工作.

4  總结

中国西部地区降水量在时间上呈现出较强的周期性和季节性，夏秋降水最多，冬春较少；在空间上呈现出南多北少，由南到北递减的趋势.本文建立了一种融合多种深度学习方法的时空集成预测模型LASBC，利用SARIMA模型捕捉降水时间序列的周期性，ARIMA模型捕捉时间近邻性， BP神经网络揭示降水量分布的空间相关性，CNN网络捕捉气象、地理因素对降水的影响，最后通过LSTM网络对4个模型的预测结果进行融合.选取高寒冻土区、西北干旱区和西南湿润区的6个主要城市的月降水量进行预测，结果表明：多模式集成模型的预测误差更低，精度更高；基于预测的月降水量，给出了6个主要城市未来10年气候可能趋于干旱或湿润的月份及预测降水量；未来10年，我国西北干旱区年均降水量基本保持稳定，高寒冻土区略有增加，西南湿润区增长趋势明显.然而，有两个方面的因素对LASBC模型的应用带来了一定程度的挑战：一是西南湿润区受厄尔尼诺现象影响，突发性极端降水事件频发影响预测精度；二是我国西部地区地域广阔，城市空间相关性明显不足影响模型性能.

参考文献：

［1］  陈菊英，齐晶，杨鹏，等．海河流域分区汛期降水量的多级预报物理模型的应用前景［C］//全国水文学术讨论会，南京：2004-12-01．

［2］  马振锋，谭友邦．预测川渝地区汛期降水量的一种物理统计模型［J］.大气科学，2004，28（1）：138．

［3］  胡盈，吴静.基于ARIMA模型的降水空间特征分析及预测［J］. 江西科学， 2021，39（1）：99.

［4］   COBAN V，GULER E，KILIC T，et al.Precipitation forecasting in Marmara region of Turkey［J］.Arab J Geosci，2021，14（2）：86.

［5］  NAYAGAM L R，JANARDANAN R，MOHAN H S R．An empirical model for the seasonal prediction of southwest monsoon rainfall over Kerala，a meteorological subdivision of India［J］.Int J Climatol，2010，28（6）：823.

［6］  HUANG Yan-yan，WANG Hui-jun，ZHANG Pei-yi.A skillful method for precipitation prediction over eastern China［J］.Atmos Ocean Sci Lett，2022，15：100133.

［7］  WANG Yan-jiao，CHEN Xian-yan，YAN Feng.Spatial and temporal variations of annual precipitation during 1960—2010 in China［J］.Quatern Int，2015，380/381：5.

［8］  CHAU K W，WU C L.A hybrid model coupled with singular spectrum analysis for daily rainfall prediction［J］.J Hydroinform，2010，12（4）：458．

［9］  HARTIGAN，Mac NAMARA S，ESLIE L M，et al．Attribution and prediction of precipitation and temperature trends within the Sydney catchment using machine learning［J］.Climate，2020，8（10）：120．

［10］  XIANG B，ZENG C F，DONG X N，et al．The application of a decision tree and stochastic forest model in summer precipitation prediction in Chongqing［J］.Atmosphere，2020，11（5）：508．

［11］  ROSTAM M G，SADATINEJAD S J，MALEKIAN A．Precipitation forecasting by large-scale climate indices and machine learning techniques［J］.J Arid Land，2020，2（5）：854．

［12］  LU Ke-sheng，WANG Ling-zhi.A novel nonlinear combination model based on support vector machine for rainfall prediction［C］//2011 Fourth International Joint Conference on Computational Sciences and Optimization，Kunming and Lijiang，China，2011：1343．

［13］  KISI O，CIMEN M.A wavelet-support vector machine conjunction model for monthly streamflow forecasting［J］.J Hydrol，2011，399（1/2）：132．

［14］   LUC K C，BALL J E，SHARMA A．An application of artificial neural networks for rainfall forecasting［J］.Math Comp Model，2001，33（6）：683．

［15］  BARATTA D，MASULLI F，CICIONI G，et al.Application of an ensemble technique based on singular spectrum analysis to daily rainfall forecasting［J］.Neural Networks，2003，16（3）：375．

［16］  NASSERI M，ASGHARI K，ABEDINI M J．Optimized scenario for rainfall forecasting using genetic algorithm coupled with artificial neural network［J］.Expert Syst Appl，2008，35（3）：1415．

［17］  LI Yue-jun，GUO Pin-wen． Application of downscaling forecast for the north of Zhejiang precipitation in summer based on the BP neural network model［J］.Trans Atmos Sci，2017，40（3）：425.

［18］  SHI X J，SHI Z R，WAN H G，et al.Convolutional LSTM network：A machine learning approach for precipitation nowcasting［C］//Neural Information Processing Systems，Cambridge，MA：MIT Press，2015：802.

［19］  DU J，LIU Y，LIU Z.Study of precipitation forecast based on deep belief networks［J］.Algorithms，2018，11（9）：132.

［20］  HA J H，YONG H L，KIM Y H.Forecasting the precipitation of the next day using deep learning［J］.Korean Inst Intell Syst，2016，26：93．

［21］  TAO Li-zhi，HE Xin-guang，LI Jia-jia，et al.A multiscale long short-term memory model with attention mechanism for improving monthly precipitation prediction［J］.J Hydrol，2021，602：126815.

［22］  MISRA S，SARKAR S，MITRA P.Statistical downscaling of precipitation using long short-term memory recurrent neural networks［J］.Theor Appl Clim，2018，134（3/4）：1179．

［23］  WU Cui-lin，HE Hong-di，SONG Rui-feng，et al.A hybrid deep learning model for regional O3 and NO2 concentrations prediction based on spatiotemporal dependencies in air quality monitoring network［J］.Environ Pollut，2023，320：121075.

［24］  DING Fei，ZHU Yue，YIN Qi，et al.MS-ResCnet：A combined spatiotemporal modeling and multi-scale network for taxi demand prediction［J］.Comput Electr Eng，2023，105：108558.

［25］  YU Cheng-qing，YAN Guang-xi，YU Cheng-ming，et al.A multi-factor driven spatiotemporal wind power prediction model based on ensemble deep graph attention reinforcement learning network［J］.Energy，2023，263：126034.

［26］  BOX G E P，JENKINS G M．Time Series Analysis：Forecasting and Control［M］.San Francisco：Holden-Day，1976.

［27］  MCCLELLAND J，RUMELHART D.Parallel Distributed Processing：Explorations in the Microstructure of Cognition：Psychological and Biological Models［M］.Cambridge，MA：MIT Press，1987.

［28］  LECUN Y，BOTTOU L，BENGIO Y，et al.Gradient-based learning applied to document recognition［J］.P IEEE，1998，86（11）：2278.

［29］  SUNDERMEYER M，SCHLUTER R，NEY H.LSTM neural networks for language modeling［R］.Human Language Technology and Pattern Recognition，Computer Science Department，Aachen，Germany：RWTH Aachen University，2012.

（責任编辑  马宇鸿）