二元共载系统退化相关的两阶段退化模型及可靠性分析
2024-05-09张帆程伯晗王鹏董磊
张帆,程伯晗,王鹏,*,董磊
1.中国民航大学 民航航空器适航审定技术重点实验室,天津 300300
2.中国民航大学 科技创新研究院,天津 300300
3.中国民航大学 安全科学与工程学院,天津 300300
随着航空系统中装备的可靠性不断提高,国产机载系统呈现高可靠、长寿命等特征,且缺乏失效数据,因此基于退化的建模方法被认为是评估系统可靠性有效的方法[1-5]。同时为保证飞行安全,航空系统多具有余度设计,系统中存在多组件共同支持系统运行。传统对于多组件系统的研究基于组件的独立性,然而由于组件的结构相关性、运行条件一致性等原因,其退化性能可能会存在随机依赖关系,这种随机依赖关系主要存在于两方面[6]:①退化进程中的相互影响关系。组件当前的退化量可能会影响其他组件的退化进程;② 组件失效的影响。最典型的为共载系统中组件负载分担关系。目前已存在大量文献分别对这两种随机依赖关系进行研究。
在对多元相关退化的建模中,Copula 函数是一类运用广泛的方法。文献[7]以Wiener 过程与Gamma 过程描述退化失效过程,选择合适的Copula 函数对多元退化失效相关性进行退化建模;文献[8]由漂移布朗运动得到目标退化模型,利用基于Vine-Copula 的多变量损伤耦合建模方法,建立了失效行为建模的相关描述模型;文献[9]改进了Vine-Copula 函数来描述性能参数之间的相关性;文献[10]在Wiener 过程与Gamma 过程的基础上,将退化过程分为线性与非线性,加入了外部因素,后用Copula 函数表述性能参数之间的相关性。然而如何选择合适的Copula 函数以及如何验证其准确性仍是待解决的难题。
将退化增量分为自身退化增量部分和相互作用影响增量部分为另一种常用的方法[11-13],文献[12-13]将相互作用影响增量部分的相关性运用了一个固定幂律公式表述。文献[14]利用因子分析法来描述相互作用影响增量部分的随机依赖关系。此外,还有部分学者通过退化速率对退化相互作用的影响进行建模[15-18],由相互作用系数表述影响程度,可以得出退化模型的数学表达式。研究[19-20]将这种依赖关系归结为共因退化进行分析。但这类模型没有建立关于部件退化过程相互影响的解析模型,也未得到相应的退化过程显式模型,这限制了对该方法的深入研究和使用。
在负载分担模型方面,大多注重于负载分配机制问题,在负载分担系统可靠性评估和寿命预测方面则采用传统的寿命统计方法[21-22]。针对缺失寿命数据的情况,将退化模型引入负载分担系统是一种可行的方法。文献[23]研究负载分担系统组件故障后前后状态之间的依赖关系,采用了Wiener 退化过程,并加入了链接函数来体现应力改变对漂移参数的影响。文献[24]通过设置应力系数,将其加入Wiener 退化模型分析了共载系统的可靠性和寿命预测。文献[25]在组件退化的基础上,考虑了随机冲击的影响,分析了共载系统的可靠性。文献[26]研究了共载系统中退化速率与冲击载荷的关系,说明退化速率的改变使系统可靠性显著降低。值得注意的是,这类基于退化的共载系统研究,仅针对单一性能参数或组件进行退化建模。建模思路与多阶段退化模型类似,如文献[24]中的图1,存活组件呈现多阶段特性,退化拐点为组件失效时间。

图1 双组件共载系统退化过程Fig.1 Two-component load-sharing system degradation process
综上所述,目前基于退化模型的共载系统的研究中,大多集中于负载变换后不同阶段退化的相关性以及内、外部应力对退化的影响方面;而基于退化模型进行多组件系统可靠性分析时,多元相关性退化模型得到广泛引用,但组件之间有除串联外的多种关联方式以及其他因素(负载分担)对组件退化进程的影响,使得多元相关退化模型在进行如共载系统的可靠性分析时会出现偏差。因此针对共载系统中存在二元退化相关的可靠性分析问题,提出了一种两阶段退化模型,并给出了系统可靠性和寿命评估方法,能够实现两种依赖关系影响下系统的可靠性分析与剩余寿命预测。
1 问题描述
在多组件系统退化可靠性分析中,对组件间退化关联性的研究是十分重要的。存在一种并联系统,系统内组件按照一定的规律各自承担整个系统的一部分负载。其中一个组件失效时,存活组件会按照一定的规律重新分配负载,当失效组件达到某一数量时,系统会表现出故障状态,这种系统称为共载系统。分析可知共载系统中组件会因负载分配策略而改变退化速率,从而呈现出阶段性退化的特点。
图1 为某双组件共载系统退化过程。第一阶段时,二者共同承担任务负载。当其中退化较快的组件到达失效阈值发生故障后退出系统,存活组件因承担所有负载导致工作负荷加重,退化速率改变,出现变点。第二阶段由存活组件承担负载直至其到达失效阈值,系统失效。
因此在多组件系统退化可靠性分析中,若在构建相关性退化模型时忽略了阶段性变化,将使可靠性预测结果偏离实际。在考虑退化关联性的情况下对共载系统进行退化建模和可靠性分析,为组件退化过程和共载系统设立以下基本假设。
1.1 退化过程基本假设
1)组件仅存在退化失效,组件退化过程服从Wiener 过程,退化过程为增长趋势,初始退化量为0。
2)组件的退化水平超过其失效阈值时,认为该组件失效,且不再影响其他组件的退化进程。
3)组件只在工作应力下开始退化,工作应力恒定的情况下,自身退化速率不变。
4)组件两阶段退化变点处的退化进程是连续的,不存在跃迁。
5)退化进程是可观测的,即可知组件失效的先后顺序。
1.2 二元共载系统假设
1)共载系统中包含有两个组件,故障阈值相同,采用并联的连接方式。当两个组件都失效时,系统失效。
2)系统载荷采用均分的方式分配给各个部件。一旦有组件失效,系统的载荷将由存活组件承担。
3)系统组件出现阶段性特征的条件是存在组件失效,使负载重新分配,在不考虑组件同时失效的情况下,可认为阶段变点前系统是可靠的。
4)若存在组件替换,则组件失效即可替换且只替换一次,忽略更换时间。替换组件具有相同的故障阈值,初始退化量为0。
2 双组件共载系统两阶段退化过程建模
在分析双组件共载系统的退化过程时,需同时考虑组件之间的相互影响对于退化进程的影响和共载状态下组件失效导致剩余组件退化速率的变化,基于此建立退化速率相关性的双组件共载系统两阶段退化模型。
2.1 基于Wiener 过程的退化模型
2.1.1 一元Wiener 退化模型
根据Wiener 过程的定义,首先建立单个组件的退化模型,设组件的退化量为Xi(t),i=1,2。定义组件i 的退化过程为非线性Wiener 退化过程[27]:
式中:ui(t)为组件的退化轨迹数学表达式;Bi(t)为布朗运动,表示退化过程中的不确定性;σi为扩散参数;函数φi(t;θ)为组件的退化速率,θ 表示影响退化过程相关参数的集合。可以发现当φi(t;θ)为一常数时,该模型为线性Wiener 退化过程。
2.1.2 二元Wiener 退化模型
设两个组件的退化量由相关的二元Wiener过程X(t)=[ X1(t),X2(t)]T描述,结合式(1),退化模型为
2.2 退化速率相关性模型建立
设组件退化速率包括:
1)βi,i=1,2,表示组件在工作应力下的退化率参数,当工作应力改变时,βi会随之改变。
2)g(Xj(t),μij)i≠j,i,j=1,2,其 中g(⋅) 表示系统中两个组件退化速率相互作用的数学表达式,μij表示组件j 对组件i 退化的影响程度,设为影响相关参数。μij的大小表示着影响程度的大小,μij为0 时表示无影响,μij为负数时表示退化影响存在抑制作用。
因此根据式(1),退化速率φi(t;θ)可表示为φi(t;βi,g(Xj(t),μij)i≠j),此时单 组件的 退化模型中退化路径模型可改写为
分析可知得出uip(t)的解析形式是推导出退化进程Xi(t)退化模型的关键,但Wiener 退化模型中含有布朗运动,存在随机性,所以很难推导出精确的Xi(t)解析表达形式。结合式(1)由Wiener 退化过程的特性可知退化路径代表着退化的趋势,可将随机布朗运动视作退化过程中的噪声[27],在分析推导退化路径函数时去掉该类随机项的影响,因此可分别近似得到组件1和组件2的退化速率表达式(4)。
在已知各函数形式的情况下,可通过一阶微分方程组得出退化率相互作用模型的解析形式:
式中:φ1、φ2为组件1和组件2 的退化速率函数。
根据式(4)可以看出,组件之间的相关性是通过uip(t)来表述的,当给定一个时刻时,uip(t)是确定值。同时根据式(4)可得到退化速率中不包含uip(t)的退化模型的解析解形式,因此可认为得到解析解后的退化模型是相互独立的[18],在二元Wiener 退化模型的基础上结合式(4),可得到双组件退化速率相关性退化模型:
式中:up(t)=[u1p(t),u2p(t)]T为退化路径向量;∑p=diag(σ12,σ22)为两个组件的退化量方差矩阵。
2.3 双组件共载系统分阶段退化模型建立
1)考虑一般情况
假设组件i 在τi时刻因负载变化导致退化速率发生变化,组件退化过程即分成两阶段,若考虑随机因素与负载之间的相互作用,则模型中的扩散参数也随之改变。因此首先给出单组件两阶段的退化模型,结合式(1)可得Xi(t)的表达式为
式中:ui2为第二阶段退化路径表达式;σi2为第二阶段的扩散参数;τi为变点时刻。
对于双组件共载系统,由分析可知当双组件均处于正常工作状态时,共同分担负载,组件间存在相互影响关系,影响着彼此的退化进程。当其中一个组件失效时,存活组件负载变化,其退化会出现两阶段的特性,同时可知,阶段变点时刻即为组件失效时刻,此时变点时刻τ1为组件1的寿命。设组件1 最先失效,其失效时间为t1,由上述分析有t1=τ1,结合式(5)和式(6)可得到双组件共载两阶段退化模型X(t)的表达式为
式中:u22(t-t1)为组件2 第二阶段的退化轨迹;σ22为组件2 第二阶段的扩散参数。
2)考虑更为复杂的情况
图2 为考虑组件替换时的退化过程,以式(7)建立的模型为基础进行扩展分析。组件1 失效后立即替换,此时双组件退化进程仍保持相互影响的状态,共同分担负载。故退化分为3 个阶段:
第一阶段在组件1 到达寿命τ1之前,双组件退化模型符合式(5)。
第二阶段更换失效组件后,设更换件的退化模型为
式中:X1s(t)为替换组件1 的退化量;u1s(t-t1)为替换组件1 的退化路径;σ1s为换组件1 的扩散参数;B1s(t-t1)为替换组件1 的布朗运动。此时系统仍处于负载分担阶段且相互影响,由式(4)知组件间的影响因素与组件的退化量相关,替换后组件退化量减小使组件2 的退化进程减缓,因此组件2 会在替换时刻出现阶段特性,结合式(3),该阶段的退化路径模型为
式中:β1s表示替换组件1 工作应力下的退化率参数;u2s(t-t1)表示替换组件后,组件2 的退化路径;X2s(x)表示替换组件后,组件2 的退化量;φ1s为替换组件1 的退化速率函数;φ2s为替换组件后,组件2 的退化速率函数。
第三阶段替换组件1 后设组件2 先失效,替换组件1承担全部负载,退化会出现两阶段的特性,阶段变点为组件2失效时刻,失效时间为t2,由上述分析有t2=τ2,结合式(5)、式(8)和式(9)得到考虑组件替换后,双组件共载两阶段退化模型X(t)表达式为
式中:us(t-t1)=[u1s(t-t1),u2s(t-t1)]T为退化路径向量;∑s=diag(σ1s2,σ22)为两个组件的退化量方差矩阵;u1s2为替换组件1 第二阶段退化路径表达式;σ1s2为替换组件1 第二阶段的扩散参数;τ2为组件2 的寿命。
3 基于退化速率相关性的共载系统可靠性分析
双组件系统在分析寿命分布和可靠度时,由于组件之间的相互影响以及组件失效带来的负载变化,导致剩余组件退化速率发生变化,系统的寿命以及可靠度无法由简单的独立关系得出。因此建立基于退化速率相关性的共载系统可靠性模型,并建立剩余寿命模型以用于剩余寿命预测。
3.1 可靠性模型
3.1.1 单组件可靠性模型
对于式(1),当φi(t;θ)为一常数βi时,式(1)为标准的线性Wiener 过程,设故障阈值为D,其寿命分布由逆高斯分布[27]给出:
其概率密度函数为
然而在一般情况下,式(1)是一个非线性Wiener 过程,在这种情况下,时间-尺度变换是一种线性变换方法,比如et、tb等,通过线性化简便寿命分布的推导并减小后续参数估计的困难。但并非所有函数都能做线性化处理,使得很难推导出精确的非线性Wiener 过程首达时间分布函数的一般形式。对于非线性Wiener 过程文献[28]基于Kolmogorov 方程推导出了Xi(t)首次达到失效阈值D 时间的近似概率密度函数:
可靠性模型为Ri(t)=1-Fi(t)。
3.1.2 单组件两阶段可靠性模型
对于服从Wiener 过程的单组件两阶段退化模型,一般可靠性模型也采用分段的描述,以线性Wiener 过程为例,在仅考虑在第二阶段失效的情况下结合式(6),令阶段变点为τi,Xi(τi)=xi,组件的寿命分布[29-30]为
然而式(14)中xi作为第二阶段退化进程的初始退化量,是随机的且服从正态分布,忽略这一特性可能会限制两阶段系统可靠性评估的准确性[31]。为了克服这一局限性,构建新的两阶段系统可靠性模型,首先建立仅考虑第二阶段失效的情况下的寿命分布:
3.1.3 双组件共载系统可靠性模型
1)考虑一般情况:设双组件共载系统的系统寿命累积分布函数为F(t),组件1 与组件2 的寿命分别为τ1、τ2,则系统寿命分布表示为:F(t)=P{τ1≤t,τ2≤t}。在第一阶段可靠的条件下,设τ1<τ2。在t1=τ1时,变点与失效组件的失效点一致,存活组件的变点是由于组件失效产生的,故变点是随组件的失效时间而改变,因此可认为变点的概率密度函数fτ1(t1)与失效组件的寿命概率密度函数一致,结合式(15)得系统的寿命分布:
式中:x2为存活组件X2在变点τ1处的退化量值;(x2,t1)为变点时间和存活组件退化量的联合概率分布。
分析P{τ1≤t,τ2≤t|τ1=t1,X2(τ1)=x2}可发现,在给定τ1的情况下,有X2(τ1)=x2,该条件符合初始值为x2的退化过程,可描述为
对比式(7)可知该条件概率所描绘的为存活组件第二阶段的退化过程,同时这也证明了在并联系统中,影响系统寿命的是系统中寿命更长的组件,即可得出第二阶段存活组件的寿命累积分布函数,P{τ1≤t,τ2≤t|τ1=t1,X2(τ1)=x2}可改写 为P{X22(t-t1)≥D-x2}=F2(t-t1),F2(t-t1)为组件2的寿命分布,结合式(14)即可得出其表达式。
因组件之间不是独立的,在同时考虑x2与t1的随机性时,两个条件概率分布(x2)和(t1)之间存在相关性,在统计学上,需考虑为二者的联合概率分布(x2,t1)。通过2.2节的描述可知,在引入退化速率相互作用模型,得出的新的退化模型解析式后,可认为两个组件是独立的,其相关系数为0,因此可得(x2,t1)=(x2) fτ1(t1)。其中,fτ1(t1)为组件1 的寿命 概率密度函数,结合式(12)或式(13)可得(x2)为X2退化量在τ1处的退化量分布,由Wiener 过程的数学特性,该变量服从正态分布:
综上所述,在式(16)的基础上,共载系统的系统寿命分布为
系统的寿命密度函数为
系统可靠度R(t)为
式中:f2(t-t1)为第二阶段退化过程的寿命分布密度函数。
2)考虑组件替换的情况:
与无组件替换的分析方法类似,分为三阶段讨论:①通过图2 分析可知,替换组件的起始退化时间与失效组件1 的失效点一致,服从组件1 的寿命分布;②因退化量改变,组件2 出现退化变点,该变点由于组件替换产生的,故变点是随组件1 的失效时间而改变。在组件2 失效前,替换组件与组件2 相互影响;③替换组件的变点是由于组件2 失效产生的,故变点是随组件2 的失效时间而改变。设替换组件寿命为τs,结合式(16)得系统的寿命分布:
式中:x1s为存活的替换组件1 在变点τ2处的退化量值(x1s,t2)为变点时间和替换组件退化量的联合概率分布。
与式(16)的分析方法一致,对式(23)进行分析,P{τ2≤t,τs≤t|τ2=t2,X1s(τ2-τ1)=x1s} 可改写为P{X1s(t-t2)≥D-x1s}=F1s(t-t2)。独立性(x1s,t2)=(x1s)(t2),其中(x1s)为X1s退化量在τ2处的退化量分布,由Wiener 过程的数学特性,该变量服从正态分布。(t2)为组件2 的寿命概率密度函数,由上述分析可知其存在阶段性,与组件1 失效有关,故(t2)为组件2 的剩余寿命概率密度函数,结合式(22)的分析方法,可得其表达式。
综上,组件替换情形作为双组件共载系统分阶段退化模型的拓展,其退化模型建立与可靠性分析均与双组件共载系统分阶段退化模型类似,因此后续工作将以双组件共载系统分阶段退化模型为重点进行分析。
3.1.4 模型数值求解
式(21)是复杂二重积分,无法得到积分原函数,难以推导出可靠性的解析解形式。因此采用蒙特卡洛模拟的方法,具体的流程如图3所示。

图3 积分近似计算过程Fig.3 Integral approximation process
由图3 所求f 为各离散点处密度函数之和,令积分域为S,则各离散化面积为S/(n1×n2),可得该二重积分的数值解为(S×f)/(n1×n2),采样的值越多,计算结果越精确。
3.2 模型参数估计
由式(3)给出的退化模型中,对于组件i,待估参数有{βi,μij,σi}。为不失一般性,假设双组件的初始退化模型均为线性模型,且组件间相互影响关系也为线性关系,则可得退化轨迹表达式:在可观 测的情况下已知组件退化顺序,设组件1 先达到失效阈值,双组件的初始退化量为均0。根据式(7)可得退化模型X(t)为
式中:uL(t)=[u1L(t),u2L(t)]T;方差矩阵∑L=diag(σ12,σ22);β22为组件2 第二阶 段的退化率参数。
采用极大似然方法,估计式(24)退化模型的参数。一般的退化速率相互影响估计方法采用定时截尾退化数据,而该方法需根据组件失效阈值对退化数据进行预处理,以变点为时间节点将退化数据分成两部分,用以估计不同阶段模型的参数。设观测间隔时间为一定值Δt,有8 个待估未知参数{ β1,β2,β22,μ12,μ21,σ1,σ2,σ22}。此模型类似于两阶段退化模型,两阶段退化模型含有退化拐点,一般认为拐点是随机变量且缺乏完全数据,参数估计十分困难。而该模型中的退化变点与组件1 的失效时间有关,变点分布与组件1 的寿命分布一致,所以该模型可根据组件1 的寿命分布,对变点及其分布参数进行估计。
由Wiener 退化过程的数学特性可知,Wiener退化过程具有独立增量,且满足正态分布。则ΔX 在不同阶段下的概率密度函数[18]为
其中,平均增量Δui为
式中:Δxi为退化增量。
可以计算得到观测数据的似然函数中各项,第一阶段组件1和组件2 的似然函数和第二阶段组件2 的似然函数如式(26)所示。
将同一类型多个组件实际的退化增量数据代入后,对该类型似然函数求和,即可得到同类型的总体似然函数,再对待估计参数求偏导,从而得到各参数的点估计值。为满足参数的无偏性,需对各参数进行无偏性检验。根据正态分布的特性,在均值参数与方差参数均未知时,均值参数是无偏的,方差参数需根据样本数进行修正。
根据Cayley-Hamilton 定理,结 合式(4)和式(24),可推导出第一阶段退化速率相互作用模型退化路径解 析解式(27)。将参数{β1,β2,μ12,μ21,σ1,σ2}代入式(27)中,结合式(24)即可得到第一阶段退化模型。再将估计的参数{ β22,σ22}代入式(24)中,可得第二阶段退化模型。
3.3 剩余寿命预测
若系统运行到tk时刻还没有失效,则其剩余寿命可定义为
由于性能参数退化过程的不确定性,导致产品的剩余寿命具有随机性。从实际应用的角度来看,需要得到剩余寿命的概率密度函数。同时基于双阶段模型,变点前后退化模型不同,因此需根据观测点建立不同的剩余寿命的概率密度函数,分为变点前观测与变点后观测两种情况。此处对于双组件系统假设τ1<τ2。
设定系统从t1到tn时刻线性能退化数据为
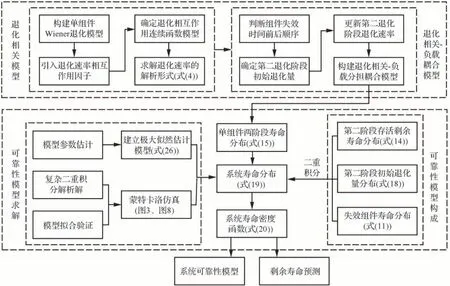
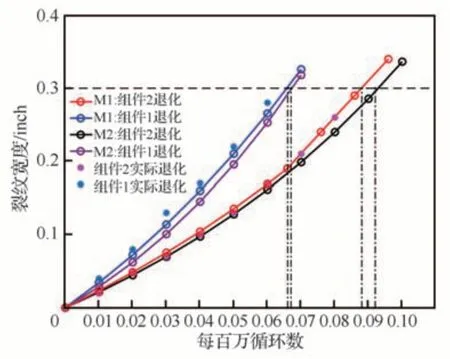
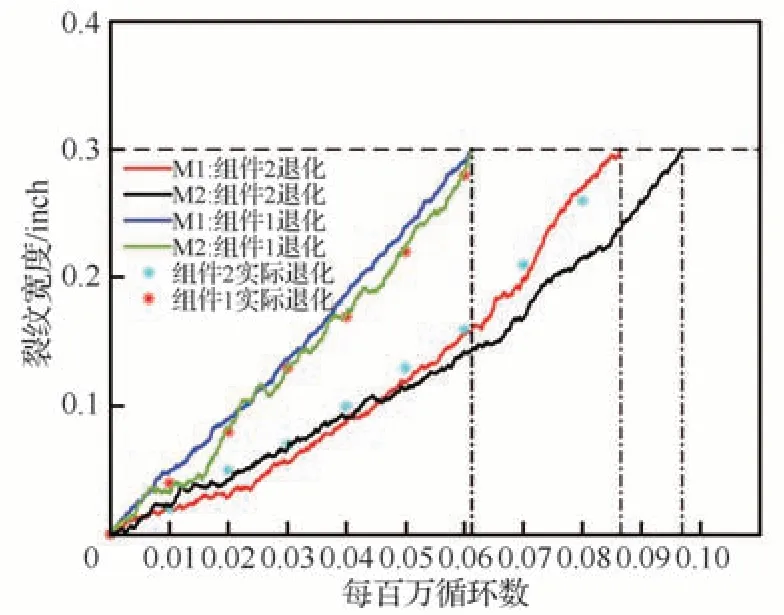
情况1当X1(tk) 结合式(13)和式(18),可分别得出tk后组件1 的变点处的剩余寿命分布和退化量分布: 第二阶段的剩余寿命分布不变,结合式(29)和式(30),可最终得出系统的剩余寿命分布的概率密度函数: 由式(19)和式(22)得X1(tk) 情况2当X1(tk)>D时 系统剩余寿命即为存活组件2 的剩余寿命。结合式(7)和式(14),可推出系统的剩余寿命分布为 4.1.1 案例描述 利用实际的退化数据验证提出双阶段退化模型和可靠性模型。一般的飞机系统中,多采用多余度设计,以保障飞机飞行的安全性。两个航空液压组件构成飞机内部的传动装置,共同驱动同一组件工作,因此两个液压组件构成了一个共载系统。液压组件因工作应力或振动等可能产生疲劳裂纹,当其疲劳裂纹到达某一阈值时,伺服燃油发生泄漏,液压组件故障,因此两个组件的疲劳裂纹退化信号可看作该共载系统的两个性能参数。案例数值数据取自文献[32],将每百万循环冲击次数看作时间。退化路径如图4 所示,展示了10 组共载系统中组件的退化过程。 图4 疲劳裂纹退化数据Fig.4 Fatigue crack degradation data 具有两个液压组件的飞机传动装置共载系统故障是由两个阶段退化过程触发的,从其中一个组件故障,到两个组件故障使系统失效。在第一阶段,由于共同应力环境,两个性能参数的退化过程是相关的。在第二阶段,生存组件承担所有传动任务,因此,组件的退化速率改变,这种现象可以从图4 中观察到。当两个组件的退化程度都达到它们的阈值时,飞机传动共载系统完全失效[33]。因此,式(7)适用于对该案例进行退化建模。 这10 组退化数据作为历史数据用以训练模型进行极大似然估计,得到模型参数的点估计值;再选取d 组的样本用于检验退化拟合程度的实际数据,所选取的样本具有明显的阶段性特征,符合所研究的背景情况。 4.1.2 系统可靠性分析总体思路 共载系统可靠性分析的总体流程包括:①基于Wiener 退化过程建立考虑负载分担的退化速率相互作用模型,得出退化解析形式;②根据退化模型与依赖耦合关系建立共载系统的可靠性模型,并基于极大似然估计与蒙特卡洛仿真的方法求解。整体思路如图5 所示。 图5 双组件共载系统可靠性分析方法Fig.5 Reliability analysis method for two-component load-sharing system 4.2.1 建立退化模型 为了说明所建立模型的有效性,将进一步开展对比研究。设考虑负载分担的双组件退化速率相关性模型为M1;不考虑负载分担,仅考虑双组件退化速率相关性的模型为M2[16]。对于组件退化速率相互作用的连续函数模型g(Xj(tj),μij)i≠j,因为组件间多种随机影响g(Xj(tj),μij)i≠j十分复杂,故采用泰勒展开取第一项,M2 与M1第一阶段退化模型一致。在假设M1 中组件1 先达到阈值的情况下,设组件1 失效时刻为τ1,其失效时间为t1,由上述分析有t1=τ1,M1 的退化模型为式(24),M2 的退化模型为 式中:β1′、β2′为组件1和组件2 工作应力下的退化速率;μ12′、μ21′为组件1和组件2 退化影响相关参数;σ1′、σ2′为组件1和组件2 的扩散参数。 4.2.2 参数估计 首先对这组数据做预处理,令其初始退化量从0 开始。假设当退化水平达到0.3,即各组件的失效阈值D=0.3时,视为组件故障。首先对M1进行参数估计,利用3.2 节给出的似然估计方法以及式(26),对图4 中的退化数据进行处理,根据组件1 的失效时刻将退化数据分为两个阶段,分别对式(24)中两个阶段退化模型的参数进行估计。M2 则利用一般的定时截尾退化数据[16],结合式(26)得到式(34)的参数估计值。表1 给出了M1和M2 的参数点估计值,结合式(27)即可得到M1和M2 退化模型中退化路径的解析形式,再结合式(24)和式(34),可得到完整的双组件Wiener退化过程。 表1 模型未知参数估计及模型比较Table 1 Model unknown parameter estimation and model comparison 4.2.3 结果分析 为了对比M1和M2 中退化路径对实际退化路线的拟合程度,以赤池信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)来衡量模型拟合数据的优良性,AIC和BIC 值越小,模型拟合程度越高。M1和M2 的AIC和BIC 值如表1 所示。然后将两种模型下预期的退化过程与实际的退化过程进行比较,图6 展示了模型退化路径的退化过程曲线对比情况,图7 展示了含有随机性的完整的Wiener过程下组件退化对比的情况。 图6 退化路径模型的退化过程曲线对比图Fig.6 Comparison chart of degradation process curve for degradation path model 图7 Wiener 退化过程对比图Fig.7 Comparison chart of Wiener degradation process 经过M1和M2 参数的估计和模型对比,结合表1和图6、图7 分析可知: 1)M1的AIC和BIC 值更小,说明在共载的情况下,M1 更加符合真实的退化过程。 2)对比M1和M2 中βi和μij数值可发现,组件1 因应力产生的退化速率较组件2 更大,且受到组件2 的影响更剧烈,所以组件1 的退化趋势更加迅速,符合图6和图7 中所展示的退化趋势。 3)结合图6 中M1和M2 退化路径可得,在组件1 到达失效阈值之前,M1和M2 的退化路径趋势都比较接近于真实的退化过程趋势。组件1 失效后,观察M1 与M2 中组件2 的退化进程,M1 因考虑了负载的变化与组件1 失效所带来的影响,退化趋势改变,其后续退化过程能很好的吻合实际退化过程,而M2 延续了之前的退化趋势,随着时间的推移,与实际退化进程误差会越来越大。 4)图7 在图6 的基础上加入了标准布朗运动,描绘的是含有随机性的Wiener 退化过程。对比图6和图7 可发现,在加入随机性后,M1 的退化趋势仍比M2 更接近实际退化情况,同时在Wiener 退化过程的基础上可以直接得到系统的寿命分布,这也体现以Wiener 过程为例的随机过程在退化模型中运用的优越性。 4.3.1 系统可靠性分析 由式(24)和式(27)可知,M1 第一阶段为非线性退化过程,第二阶段为线性退化过程,因此结合式(15)、式(18)和式(21),代入表1 中的参数估计值,即可得到M1 的可靠性模型解析形式。 为了验证式(21)和式(22)的有效性和分析的准确性,将M1 的解析解和模拟解进行了比较。采用蒙特卡洛仿真的方法模拟组件退化过程,结合组件间相互影响关系和负载分担,得到大量系统失效时间从而得出寿命分布与概率密度函数仿真解。该案例的退化仿真过程流程图如图8所示。 图8 蒙特卡洛退化仿真流程Fig.8 Monte Carlo degradation simulation process 通过退化过程模拟程序和组件失效阈值生成足够多故障次数,将失效时间频率寿命直方图与式(22)给出的解析寿命密度函数进行比较,其中模拟过程运行了5 000次,如图9 所示。 图9 基于两种解的系统寿命概率密度对比图Fig.9 System lifetime probability density comparison plot based on two solutions 由结果图仿真数据和解析分布对比可以看出,所提的可靠性模型可较为精确地得到系统的寿命分布。同时基于仿真数据可得出系统可靠度的仿真解,将可靠度的解析解和仿真解进行比较,如图10 所示,可见二者结果吻合较好。 图10 基于两种解的系统可靠度对比图Fig.10 System reliability comparison chart based on two solutions 4.3.2 结果分析 根据式(34)可知M2 双组件退化过程均为非线性,同时结合2.2 节的独立性分析,可得出M2的可靠度模型为 式中:F1(t)、F2(t)为 服从式(13)的累积分布函数。 在4.3.1 节分析的基础上,对比了M1 与M2下系统、组件1和组件2 的可靠度曲线,如图11所示,其中M1 组件2 的可靠度曲线由式(15)求得。 图11 M1 与M2 可靠度对比图Fig.11 M1 and M2 reliability comparison chart 经过M1和M2 可靠性曲线的对比分析可知: 1)对比M2 下组件2和系统的可靠性曲线,二者曲线几乎重合,因此M2 的可靠性模型无法体现组件1 失效对系统可靠性的影响。 2)对比M1和M2 系统可靠度曲线,可以看出M1 可靠性更低,结合图6和图7 可以得出M1比M2 先失效,因此该差距是合理的。 3)对比M1 中组件2和系统可靠性曲线可发现并不重合,这是因为M1 可靠度模型式(21)中描述了组件1 失效对组件2 退化的影响。同时发现组件2 的曲线更加陡峭。分析可知,可靠性的陡峭程度反映的为该处寿命密度函数,越陡峭说明其方差越小,寿命集中于期望附近。因为系统可靠度有组件1 失效的影响,随机性更强,方差更大。 首先根据图4 的退化数据,在除去初始退化时刻后,列出8 个观测点,根据组件1 的失效时刻,剩余寿命建模包括: 阶段1:当观测点在组件1 失效之前时,结合式(31)可得每个观测点处的剩余寿命的概率密度函数。 阶段2:当观测点在组件1 失效之后时,结合式(33)可得每个观测点处的剩余寿命的概率密度函数。 根据建立的模型,分析了不同观测点处剩余寿命的概率密度函数,并将观测点处所预测的剩余寿命期望均值与剩余寿命真实值对比,并给出了剩余寿命期望均值95%区间估计,如图12和图13 所示。 图12 不同预测时刻系统剩余寿命的概率密度函数Fig.12 Probability density function of remaining lifetime of the system at different prediction moments 图13 不同预测时刻系统剩余寿命期望均值与区间估计Fig.13 Mean and interval estimation of system remaining life expectations at different prediction moments 从图12 中可以看出,相比而言前几个时刻的预测结果与真实值相差较大。从实际出发可分析到,在系统早期的使用中失效的概率很小,因此早期预测结果不准确是可以接受的。从整体上看,剩余寿命预测均值近似拟合其真实值,且逐步向真实值逼近,同时结合图13 可看出95%区间估计包含了真实值。为了具体化实际值与预测值之间的差异性,采用相对误差表述,如表2所示。说明了该模型可适用性,为后续维修决策等提供了便利。 表2 各观测点剩余寿命相对误差值Table 2 Relative error value of the remaining life of each observation point 建立了基于退化相关的双组件共载退化模型,在退化进程相关和负载分担的情况下预测组件的退化趋势,并进行系统的可靠性分析。①采用Wiener 退化过程,模拟由于未观察到的环境因素或环境因素对退化过程的未知影响而导致的无法解释的随机性,同时具有良好的数学运算性质。②模型具有实际的物理意义,退化速率相互影响模型能够描述两个组件退化进程之间的相关关系,且能得出退化模型的解析形式。③基于阶段性退化过程,构建了双组件共载系统的可靠性模型,同时建立了不同阶段下系统的剩余寿命模型。该模型能够描述组件失效对于系统可靠度的影响。 基于二元退化相关的共载系统可靠性分析方法综合考虑了退化相关性和负载分担对于系统的影响,给出了基于退化模型的共载系统可靠性解析式。将蒙特卡罗模拟法应用于可靠性分析中,解决了计算可靠性解析解中复杂的多重积分运算情况,为后续实例验证提供便利。 所提方法为双组件共载系统可靠性分析提供了可行思路,提高系统可靠性预测的精度。但更常见的共载系统是基于k-out-of-n 的多组件系统;同时,针对不同类型的组件,应力变化对于退化速率的影响是不同的。因此针对多组件共载系统可靠性及应力与退化速率关系的进一步分析,提出更通用的退化模型以及更准确的退化速率表达形式,是后续研究的重点。4 算例分析
4.1 系统概述
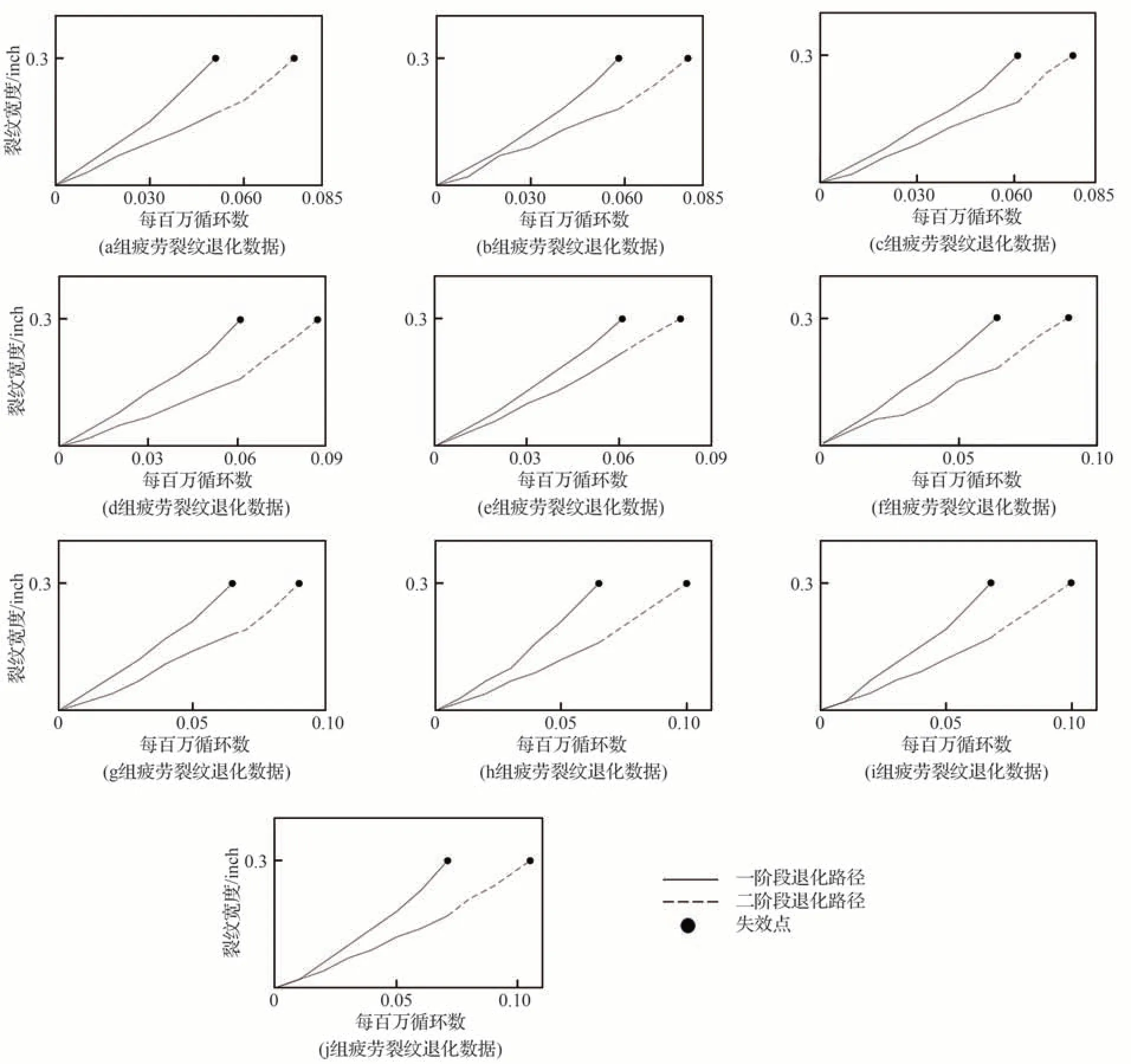
4.2 退化过程分析

4.3 可靠性分析
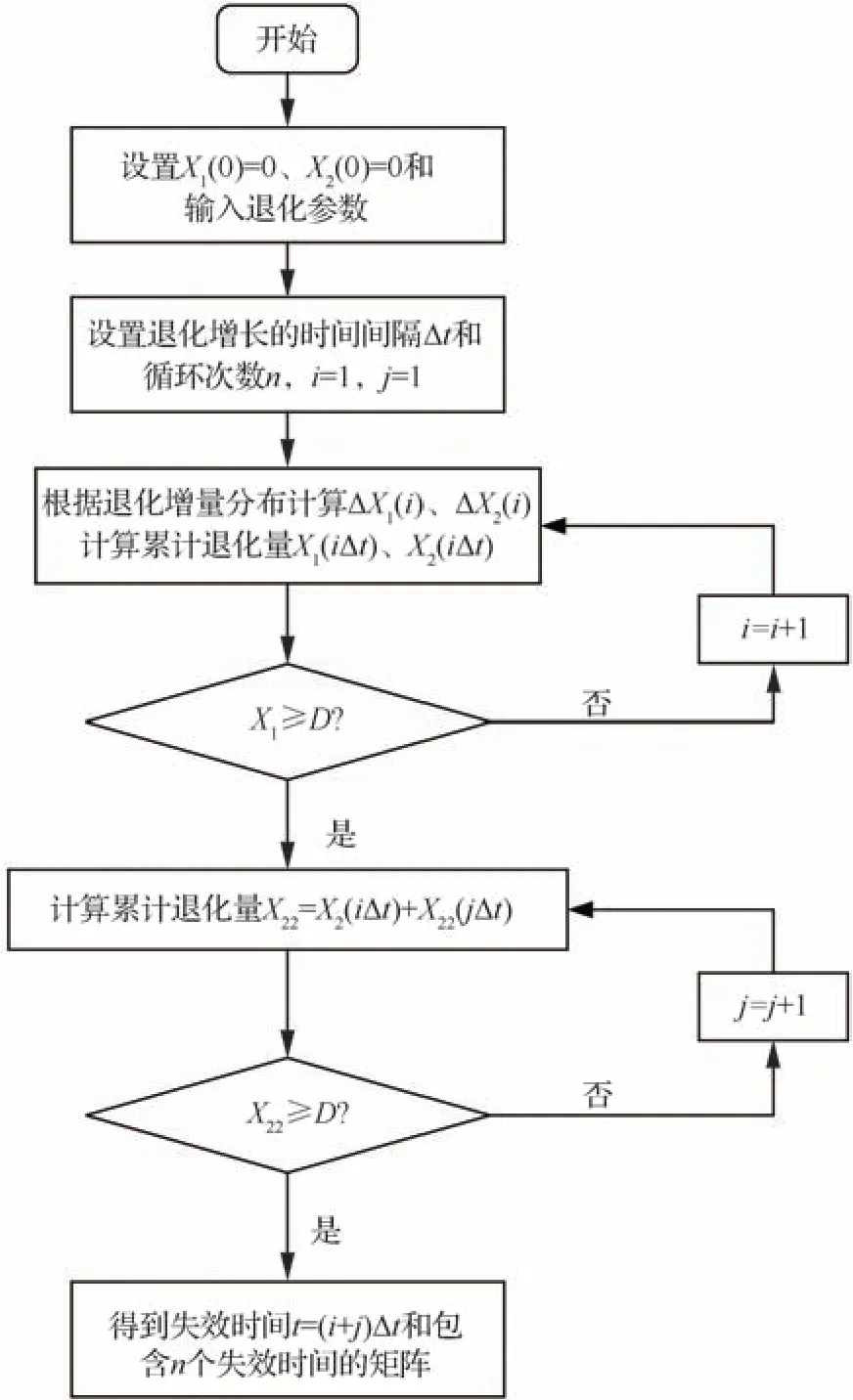

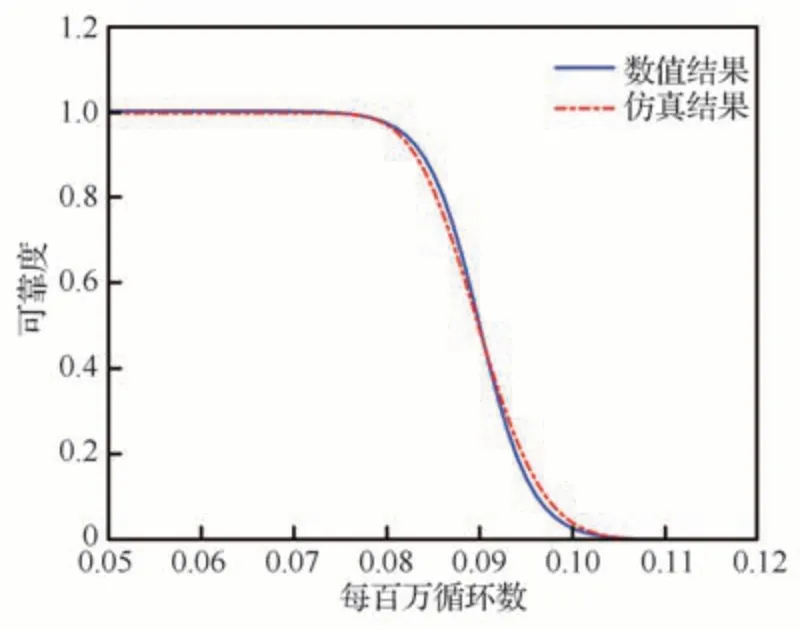

4.4 剩余寿命分析



5 结论
