基于机器学习的材料弹性性能预测及可视化分析

林轩杰，江汉同，李 倩，周玉玲，臧怀娟，任永生，詹 曙，马文会

1) 合肥综合性国家科学中心人工智能研究院，合肥 230601 2) 合肥工业大学计算机与信息学院，合肥 230601 3) 真空冶金国家工程实验室，昆明 650093 4) 昆明理工大学冶金与能源工程学院，昆明 650093

随着科技的快速发展，航空航天、人工智能、人造太阳等这些曾经不为人知的新兴词汇如今已从概念逐渐变为现实，影响着人类的生活与生产方式.新兴领域取得的突破伴随着新产物的出现，都和新材料的研究与发展有着密不可分的联系[1].新材料是新兴产业发展的基础，几乎所有的重大科技革新都与新材料的出现有关[2].2011年美国提出“材料基因组计划(MGI)[3]，材料基因组融合了材料的高通量计算、高通量制备、高通量检测及数据库系统[4]，形成新材料创新发展的基础条件和能力.材料基因工程是材料领域的颠覆性前沿技术，将对材料研发模式产生革命性的变革，全面加速材料从设计到工程化应用的进程，大幅度提升新材料的研发效率[5].材料基因工程是材料领域的颠覆性前沿技术，将对材料研发模式产生革命性的变革，全面加速材料从设计到工程化应用的进程，大幅度提升新材料的研发效率，缩短研发周期，降低研发成本，促进工程化应用.高通量计算是以量子力学中的薛定谔方程作为理论基础，以材料内部粒子空间分布(晶体学信息文件CIF)作为输入，设置所需参数，预测材料的相关属性(包括动力学、热力学和结构性质等）并导入材料数据库.然而高通量计算需要消耗大量的计算资源与时间[6]，不同元素构成的材料，如果元素种类、配比、空间结构等存在差异，生成材料的性能也大不相同，仅仅采用高通量计算进行盲目的检索，并不是一种明智的举措.近些年来，随着基于第一性原理(DFT)[7-8]模拟仿真方法[9-10]的成熟运用，产生了大量的基于高通量计算的材料属性数据，材料数据库也不断扩展.同时，机器学习、大数据挖掘的快速兴起，使得基于大数据和机器学习的材料性能预测方法逐渐成为了可能[11-12].从已有的材料数据库中进行数据挖掘，提取有用的特征，将这些信息应用于未知材料领域的性能预测，与DFT相比可以使计算量下降多个数量级.

目前，将机器学习方法应用于材料性能预测领域的研究取得了一定的进展.Ramprasad等[13]概括了一些数据驱动的材料信息学的成功应用，特别指出特征描述符的重要性，认为选择合适的特征描述符在确定控制复杂现象的关键物理因素方面非常有效，Fujimura等[14]基于第一性原理(DFT)，将理论和实验数据集相结合，利用机器学习方法以预测材料在373 K的导电性，可以加速锂超离子导体材料设计.Meredig等[15]利用DFT理论计算得到数据库并构建机器学习模型，由此产生的模型可以预测材料的热力学稳定性，与DFT计算结果进行对比，发现拟合精度较好的同时，计算量降低6个数量级，计算速度得到了较大的提升，说明机器学习方法适用于高通量计算材料筛选.Xu等[16]利用组分替换策略，在已有的高通量计算材料数据的基础上产生大批量相似新型材料体系，通过皮尔逊线性相关性系数图谱进行特征选择，使用基本的机器学习回归算法，有效且准确地预测了类金刚石组分替换产物的带隙值.Wang等[11]总结了基于机器学习的热点材料的研究进展，指出了有限的数据量是机器学习方法实现应用的主要障碍.材料研究进展到目前为止，通过结合机器学习技术与高通量计算手段来研究材料体系大都是进行性能预测，对于特征描述符对材料性能影响的可视化分析的研究较少.在材料性能预测中，特征描述符是预测材料性能的决定性因素[17]，找到特征和目标属性之间隐藏的映射关系是机器学习的主要目标.通过可视化可以更加直观了解和分析特征描述符在材料属性中的影响程度和相关性，对于选择合适的特征描述符提升材料属性预测的准确性和理解材料内在机理具有重要意义.

本文通过实验，将不同的特征选择方法和机器学习模型进行组合和比较，寻找最优的组合方案来预测材料的弹性模量[18]，并设计交互式可视分析系统，将各个特征描述符对材料弹性预测的性能影响进行直观表示，探究单个特征描述符对弹性模量进行范围预测和弹性模量反推特征可行域的可能性，为加快材料粗筛速度和深入了解弹性性能的影响因素提供参考.

1 研究方法

本文通过开源的无机化合物材料数据库Materials Project[19]获取材料数据集.数据库内含基于第一性原理高通量计算得到的材料属性，选择弹性模量中剪切模量Voigt及Reuss的平均值Gv和Gr,体积模量Voigt及Reuss的平均值Kv和Kr四个参数作为目标属性，选择数据库中含有的材料信息作为输入，首先进行不同方式的特征选择操作，构建对于弹性模量具有有效预测能力的特征子空间，然后在训练集上学习获得不同类型的机器学习模型来预测目标属性，计算并比较预测精度，得到最优的性能预测组合.然后通过可视化的手段分析各特征描述符对弹性模量预测的影响程度，找出对于弹性模量预测最重要的特征描述符，探究重要的特征描述符独立预测弹性模量范围和弹性模量反推特征可行域的可能.实验流程如图1所示，特征选择方法、机器学习模型和实验的具体流程将在下文进行介绍.

1.1 数据集

文中采用的硅材料数据集来源于MP（Materials Project）数据库.MP数据库是由加州伯克利大学劳伦斯实验室（Lawrence Berkeley National Laboratory）及麻省理工学院（MIT）在2011年发起的项目，旨在通过计算所有已知材料的属性，挖掘材料特性，加速材料研究的创新.本实验中选取的是V2021.03.22版本，数据库中共收录无机化合物131613种，可为深度学习提供大量可靠的材料数据.MP数据库还可通过材料应用编程接口（MAPI）和开源Python材料基因组学（Pymatgen）[20]材料分析包提供材料的相关数据和分析.因此，数据获取步骤是利用MAPI从MP数据库中检索硅材料的相关信息作为机器学习的目标输出.本文选择了20种常见的金属非金属元素构成的材料.然后，对候选材料进行筛选，因为MP数据库中并不是所有材料都计算了弹性模量，因此弹性模量属性为空的材料需要去除.除此之外，因为数据库中材料的弹性模量是通过高通量计算得到的理论值，并没有考虑晶体系统的Born-Huang弹性稳定性标准[21]，如果高通量计算的弹性张量特征值是负的，说明违反了稳定性标准，表明该化合物在零温度下机械不稳定或者计算错误，考虑到机械不稳定或者弹性张量计算错误的材料会对预测结果造成干扰，本文还将弹性模量有警告提示的材料去除.最后，再筛选去除重复检索的化合物(例如CuFeS2可由Cu元素检索得到，但会被Fe元素重复检索)得到1143种无机化合物作为数据集.

1.2 特征描述符

利用MP数据库和Pymatgen获取数据集材料的40个特征描述符，这些特征描述符可分为3个方面: 14个化合物基本属性(能量，每原子能量，原子形成能，体积，原子数，Ehull，空间群编号，密度，总磁化强度，最大电负性，元素数，最低未占分子轨道，金属特性，平均电负性)，20个元素属性(原子序数，熔点；分别填充到10个维度)，6个晶体空间结构属性(键长，角度）.其中，因为构成化合物的元素种类并不都是相等的(例如SiO2由两种元素构成，而CuSO4则有三种)，为满足数据等长，设置构成材料的元素数量为10个单位长度，若构成化合物的元素种类少于10种，用“0”对“原子序数”和“熔点”进行填充;“键长”和“角度”分别有3个子属性:a，b，c和α，β，γ.这40个特征描述符作为实验的输入特征集，然后从MP数据库中获取化合物的Gr，Gv，Kr，Kv数据，分别选取其中的一种作为预测目标，构成实验的输出目标集.

1.3 特征选择

特征输入是机器学习的关键环节，不同的特征描述符对于预测目标的影响是不同的.例如在预测材料稳定性时，分子内部相邻两个原子(或离子)间的相互作用力强弱起到了决定性作用.特征描述符之间也可能会有一定的相关性，例如粒子平均能量由分子总能量和粒子数量决定.特征描述符的细粒度也有差异性，这里的细粒度可以理解为影响因素的复杂程度，例如带隙相较于体积，是更加精细的特征描述符.如果需要提高预测目标的准确性，特征描述符必须足够精细且与预测目标强相关，以便模型能够对细节进行学习.一般来说，特征描述符越精细.独立特征数量越多，预测准确度也越高，但拟合难度也更高，更加费力.相反，较为粗糙的特征集合，可以对预测目标进行范围估计，用于材料的快速初始筛选.因此，材料性能预测任务的实质就是预测模型学习特征描述符与目标性能之间的映射关系，其中每个特征都作为一个因素影响到预测结果.特征选择的目标就是找到一个特征子空间，使特征之间尽量相互独立且能较好的表征预测结果，从中除去无关变量和冗余变量，改善预测性能的同时减小计算量.特征选择的方式主要有三种: 过滤式选择、包裹式选择和嵌入式选择.

1.3.1 过滤式特征选择

过滤式特征选择按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数来选择特征.本文中的特征属性既有离散型也有连续型，而且除了补零部分外，特征取值基本不同，所以采用单变量特征选择，主要原理是分别单独计算每个变量的某个统计指标，根据该指标来判断哪些指标重要，剔除那些不重要的指标.本文采用了皮尔森相关系数来分析并识别出具有高度相关的特征，这种方法较简单且易于运行，通常对于理解数据有较好的效果.皮尔森相关系数的计算公式如下:

式中，假设有两个变量X和Y，mean()代表变量的均值，std()代表变量的标准差.这里计算出的相关系数严格来说是样本相关系数，还需要从样本推论到总体，做假设检验.假设输入(X)和输出(Y)都满足正态分布，利用样本提供的信息对提出的假设进行检验.下面令:

式中，n表示每个组别的样本大小，ρ代表皮尔森相关系数.如果X和Y都服从正态分布，则f服从F(1,n-2)，这个统计量用来检验正态假定下总体中两个变量之间的相关性.f值越大，说明特征和目标参数之间的相关性就越大.因此，根据f值的大小进行特征选择.

1.3.2 包裹式特征选择

本文采用了递归特征消除(Recursive feature elimination, RFE)，使用一个基模型来进行多轮训练，每轮训练后移除若干权值系数的特征，再基于新的特征集进行下一轮训练.主要操作为对特征含有权重的预测模型，RFE通过递归减少考察的特征集规模来选择特征.首先，预测模型在原始特征上训练，每个特征指定一个权重.然后，那些具有最小绝对值权重的特征从特征集中去除.如此往复递归，直至剩余的特征数量达到所需的特征数量.

1.3.3 嵌入式选择

基于机器学习模型的特征选择方法也是一种主流的方法.有些机器学习方法本身就有对特征进行打分的机制，很容易将其运用到特征选择任务中.通过学习模型在训练过程中自动进行了特征选择，当维数较大样本较少时，容易陷入过拟合.故加入正则项，使用L1范数作为惩罚项使得大部分特征对应的系数为0，更容易得到稀疏的解，从而减少特征的维度以简化任务.常用的稀疏预测模型有LASSO和LinearSVC.其中LASSO运用于回归任务，LinearSVC应用于分类任务，本文采用LASSO进行特征选择.

1.4 可视化分析

对特征描述符的重要性进行评价，有助于分析影响材料弹性模量预测的关键特征属性，还能够了解材料空间结构、电子结构、能量等属性与弹性性能之间的内在规律.本文设计了材料弹性预测可视化系统，通过图表直观显示特征描述符对弹性模量的影响程度，进而判断特征对目标变量的重要性.除此之外还对训练集和测试集的数据可视化，表征弹性模量的变化范围，显示机器学习方法的拟合性能.还通过可视化分析，探究重要的特征描述符独立应用于弹性模量范围预测的可能，为指定性能要求的新材料初步快速筛选提供了新的解决思路.

1.5 回归模型

根据数据库提供的丰富材料特征数据，通过机器学习的模型学习关于特征描述符-目标属性的映射关系，预测未知目标属性的值.由于材料的弹性模量均为连续值，因此对弹性模量进行预测属于机器学习中典型的回归问题.文中使用回归任务中较为常用的4种机器学习回归预测模型:LASSO[22-23]、SVR[24]、GBDT[25]、MLP[26].这四种算法具有不同的模型特性和优势，LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选和复杂度调整，具有良好的线性表达能力;SVR可以用来处理非线性数据，通过选择不同核函数的非线性映射将数据投影至特征空间，然后在特征空间使用线性回归，具有低维的计算成本而实际的回归效果表现在高维上;GBDT在传统机器学习算法里是对真实分布拟合的最好的几种算法之一，预测性能较好; MLP是当前机器学习领域普遍应用的算法，具有很强的自适应学习能力，能处理复杂的非线性系统.探索这些算法在弹性预测任务中的表现，与特征提取方法组合，获得最优的预测模型.

1.5.1 LASSO回归

LASSO是以缩小特征集为思想的压缩估计方法.它在损失函数中引入了正则化L1范数惩罚项，减少输入变量数量进而控制模型的复杂度，可以解决线性回归出现的过拟合问题.LASSO回归的损失函数为:

式中，m表示样本大小，hθ()是回归模型，w是回归系数.λ是正则化参数，作用是控制平衡拟合训练的目标和保持参数值较小.

1.5.2 SVR

SVR是支持向量机(Support vector machine, SVM)对回归问题的一种运用.SVR回归是要找到一个回归平面，让一个集合的所有数据到该平面的距离最近；SVR认为只要f(x)与y(预测值和真实值)的偏离程度不要太大，既可以认为预测正确，不用计算损失.具体的说就是设置阈值τ，只计算|f(x)-y|＞τ的数据点的loss.SVR的目标函数为:

式中，C为正则化常数，ω为划分超平面的法向量，lτ为损失函数:

由于特征空间维数可能很高，高维计算通常是困难的，所以需要设计核函数，使得非线性回归问题在经过核函数的转换后可以变成一个近似线性回归的问题.SVR引入核函数之后，可重写为:

式中，k(x,xi)为核函数，ai为拉格朗日系数，ai≥0，b为偏置系数.常用的核函数有线性核、多项式核、高斯核，根据具体问题选择性能最优的核函数.

1.5.3 GBDT

GBDT全称梯度下降树，是通过采用加法模型以及不断减小训练过程产生的残差来达到将数据分类或者回归的算法.经过多轮迭代，每轮迭代产生一个弱分类器，每个分类器在上一轮分类器的残差基础上进行训练.训练的实质是通过降低偏差来不断提高最终分类器的精度.GBDT算法可以看成是M棵决策树组成的加法模型，其计算公式如下:

式中，x为输入样本，p为模型参数，Tree为分类回归树，K为每棵树的权重.

1.5.4 MLP

MLP是一种前馈人工神经网络模型，其将输入的多个数据集映射到单一的输出的数据集上.MLP的一个重要特点就是多层，第一层称之为输入层，最后一层称之有输出层，中间的层称之为隐藏层.MLP并没有规定隐藏层的数量，因此可以根据各自的需求选择合适的隐藏层层数.因为在上述预测弹性模量的任务中，数据集并不大且维度较低，因此为了避免过于复杂的神经网络造成过拟合现象，本文只涉及了一个隐藏层，选择MSE损失作为回归损失函数.

1.6 评价指标

文中主要采用均方根误差Rmse和拟合优度R2作为预测模型性能评价指标.Rmse衡量的是真实值和预测值之间的误差，R2的最大取值为1，取值越接近1表明拟合程度越好，其计算方法如下:

式中，y代表真实值，代表模型预测值，y¯代表样本均值，m代表样本个数.

2 实验结果与分析

采用上文提到的3种特征选择方法和4种机器学习模型进行组合，总共得到9种组合方式来对材料的弹性模量进行预测.选用MP数据集中常用元素构成的1143种无机化合物作为数据集，通过十折交叉验证将数据集随机分成10组，以Rmse和R2作为评价指标，显示模型的预测性能.

2.1 预测结果与分析

基于材料训练集，对9种不同的回归组合算法进行网格搜索调参，产生各自的最优回归模型，将其在测试集上的弹性模量预测结果与MP数据库中直接高通量计算的弹性模量进行比较，Rmse和R2指标如表1、表2所示.图2为材料的4种弹性模量在Pearson-GBDT模型下的真实值-预测值图，较为直观地展示了预测结果.

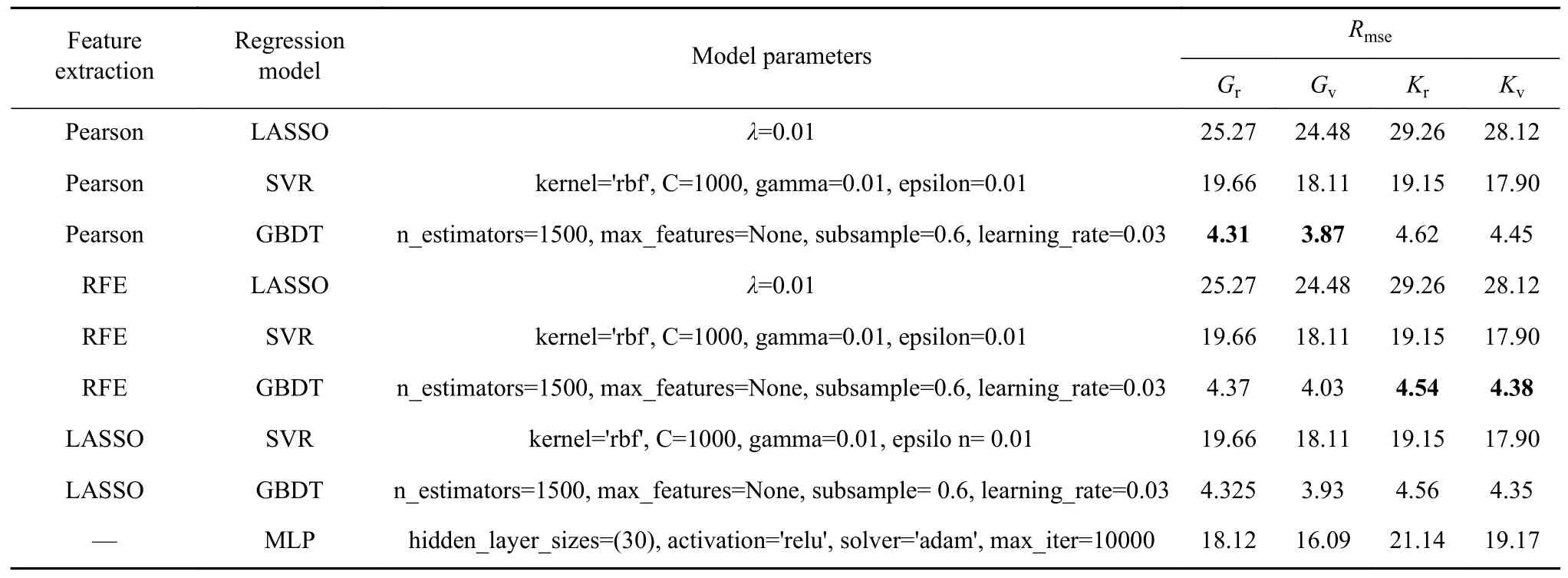
表1 组合模型对4种弹性模量的预测结果(Rmse值)Table 1 Prediction results of the four elastic moduli of the combined model (Rmse)

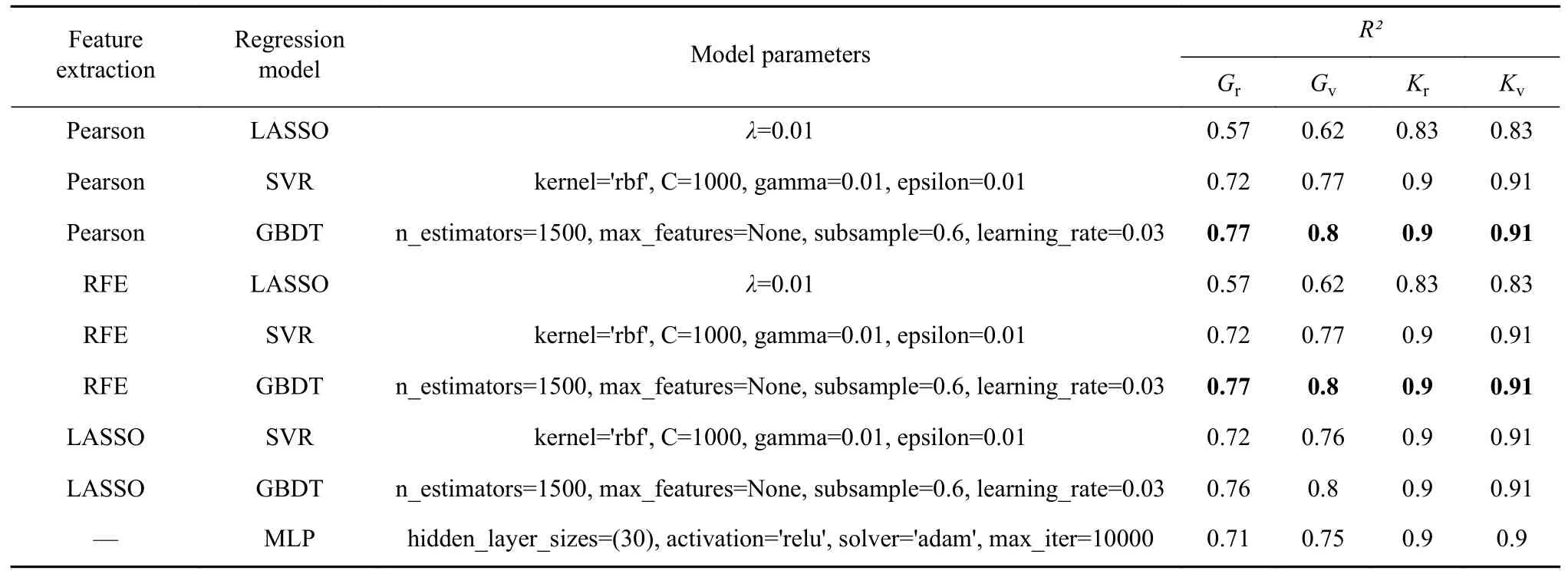
表2 组合模型对4种弹性模量的预测结果(R²值)Table 2 Prediction results of four elastic moduli of the combined model (R² value)

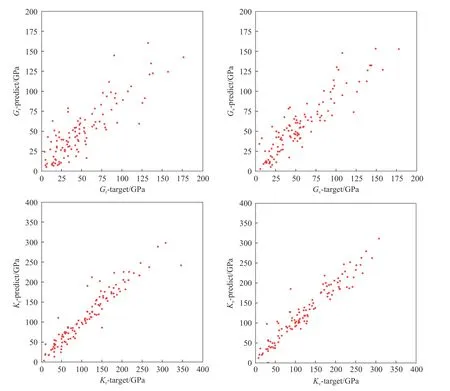
图2 4种弹性模量的最佳预测模型真实值-预测值图Fig.2 Plot of true and predicted values of the best prediction model for four elastic moduli

结合表1、表2中可以看出，Pearson、RFE和LASSO这三种特征提取方法的效果基本相同，Pearson和RFE稍好于LASSO.在回归模型选择上，GBDT对于弹性模量的预测效果最好，SVR与MLP的效果较好，而LASSO的预测效果最差.最佳的模型组合是Pearson或RFE与GBDT的预测模型，对Kr和Kv的预测拟合优度分别达到了0.90和0.91，Gr和Gv的预测性能相比于体积模量K稍差，但也达到了0.77和0.80.GBDT通过采用加法模型以及不断减小训练过程产生的残差来达到将数据回归，其优点是可以灵活处理各种类型的数据，包括连续值和离散值，在相对较少的调参时间情况下，预测的准确率也比较高，在使用一些健壮的损失函数，对异常值得鲁棒性非常强.而在实验中，数据集材料包含40个特征，这些特征描述符可分为3个方面，GBDT能灵活处理这些特征描述符，从而得到最优的预测.总的来说，组合模型对于弹性模量的预测表现较好，其中特征提取方法对于性能的预测影响不大，预测性能的主要影响在于回归模型的选择上，体积模量K的预测性能好于剪切模量G，我们认为这是因为材料的体积模量与单位体积化学键的键能和密度关系很大，而输入的特征描述符包括了体积、键能和密度的相关信息，因此模型较容易从中学习特征-性能的映射关系，而影响剪切模量的因素相对比较复杂，输入端缺失部分重要的特征描述符，是导致剪切模量预测性能差于体积模量的主要原因.

2.2 可视化分析

下面通过可视化的方式，分析影响无机化合物弹性模量预测的关键材料属性，通过皮尔森特征提取获得各特征属性的f值，f值大小与特征重要性成正比，可作为特征得分，从而绘制对应的特征重要性评价图.如图3所示，直观显示了影响弹性性能预测的重要材料属性.

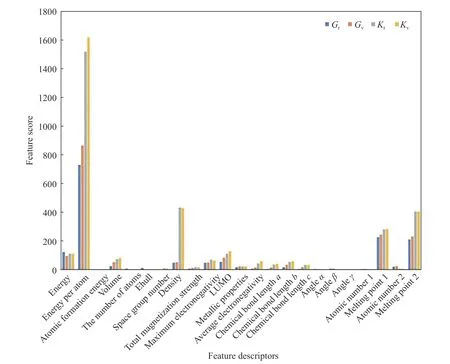
图3 特征重要性评价图Fig.3 Evaluation of feature importance

其中最重要的4个特征描述符的相对影响率在表3中进行了总结.为探究单个特征描述符与弹性性能预测的关系，本文还绘制单个特征值-弹性模量预测值散点图.如图3所示，我们发现一个重要的特征描述符可以从特征-目标的映射关系中推导出目标属性的范围.反过来，一个大致的属性范围也可以用来粗略估计关键特征的相应数值.例如每原子能量-Kv的预测关系图4(c)中，选择每原子能量2 eV，则Kv的范围大致在0～100 GPa;同样若已知Kv为300 GPa，则材料的每原子能量大概在8～10 eV之间.这个规律可以用于材料弹性预测的粗筛(不需要较为精确的目标值)，降低对输入特征数的要求.还可以根据所需的弹性目标值，反推材料的关键特征，从而应用于新材料的发现与合成.

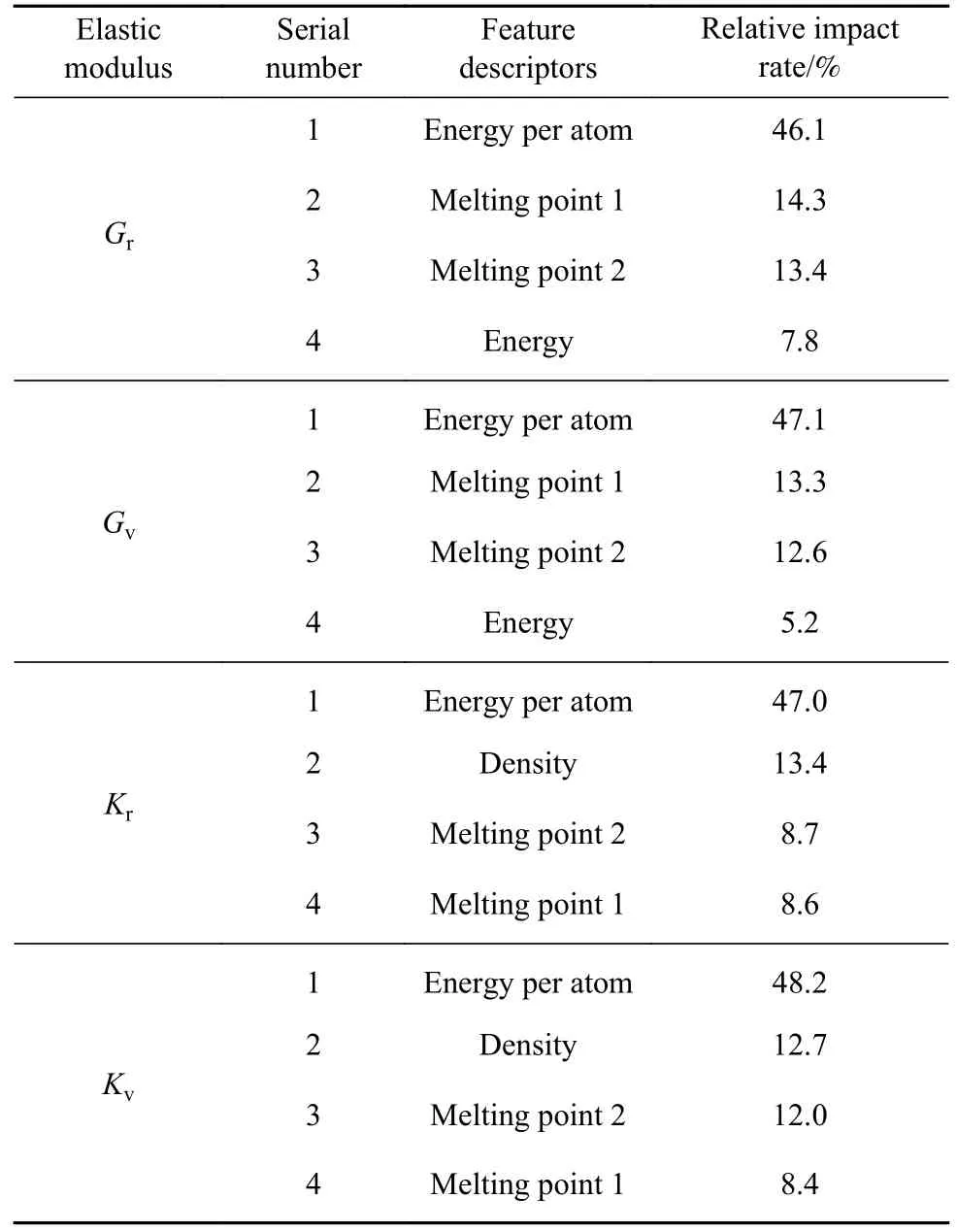
表3 最重要的4个特征描述符的相对影响率和排序Table 3 Relative impact rates and rankings of the four most important feature descriptors

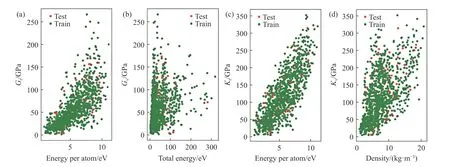
图4 单特征-弹性模量预测图.(a)每原子能量-Gv预测关系；(b)总能量-Gv预测关系；(c)每原子能量-Kv预测关系；(d)密度-Kv预测关系Fig.4 Single feature-modulus of the elasticity prediction plot: (a) prediction of the energy-Gv relationship per atom; (b) prediction of the total energy-Gv relationship; (c) prediction of the energy-Kv relationship per atom; (d) prediction of the density-Kv relationship

2.3 交互界面

为方便用户对材料性能进行分析研究，本文提供了一个用于材料弹性预测和分析的可视分析界面，帮助用户从中获取材料的相关信息与预测分析.系统交互界面如图5所示，其分为4个区域.区域A是数据导入和参数设置的主要区域，该模块内含常用材料数据集的下载地址，用户可以导入相关数据集，也可以根据自己的需求自定义数据集.用户可根据自身需求选择对应的特征和弹性性能并输入相关数值，作为单特征-弹性模量范围预测的输入参数.区域B是预测模块，会根据区域A的参数设置预测材料弹性性能，还可以计算特征值和弹性预测范围，应用于材料的筛选任务.区域C是图片选择模块，显示了数据分析的不同类别，用户在此区域进行选择，结果将展示在可视化分析模块中.区域D是可视化分析模块，用户可获取弹性模量的真实值－预测值图、特征重要性评价图、单特征描述符-弹性模量预测图和特征相对影响图，这些统计图是模型预测性能和特征-弹性模量相关性的直观显示，方便用户了解弹性预测的深层次.

图5 弹性预测可视化系统交互界面Fig.5 Elastic prediction visualization system interface

3 结语

文中使用了3种特征选择方法和4种机器学习模型组成9种组合模型，对MP数据库中常用元素构成的1143种无机化合物的弹性模量进行了预测，并进行模型性能比较.

(1)实验发现3种特征选择方法对于预测的性能影响差异很小，而不同的机器学习模型存在较大差异，其中GBDT的预测性能在4种方法中是最优的，Pearson/RFE-GBDT组合模型的预测结果最好，对Kr和Kv预测的拟合优度分别达到了0.90和0.91，GBDT能灵活处理数据集中不同类型的特征描述符，从而得到最优的预测.

(2)对特征描述符的预测重要性进行量化分析，发现每原子能量、元素熔点、总能量、密度等特征描述符，在弹性性能预测的过程中具有较大影响，重要的特征符可以单独作用于弹性预测，得到材料的弹性预测范围，弹性模量也可反推材料关键特征属性的可行区间，此发现有助于加快材料的粗筛和新材料的发现.

(3)设计了针对材料弹性预测的可视分析系统，该系统集数据收集与可视分析于一体，将实验用到的材料数据库、机器学习模型、数据分析算法嵌入其中，方便用户根据自身需求获取相关数据，增强材料弹性性能研究的分析能力，对新型功能材料的研发具有重要意义.