基于前馈模型预测控制的类车机器人路径跟踪

白国星，伊力夏提·伊力哈木江，付薛洁，孟 宇，刘 立，顾 青

1) 北京科技大学机械工程学院，北京 100083 2) 北京科技大学顺德研究生院，顺德 528399 3) 烟台南山学院智能科学与工程学院，烟台265713

类车机器人（Car-like robot）即采用前轮转向形式的移动机器人[1-6]，其转向结构、驱动形式与乘用车类似.相比差动机器人、全向轮机器人等其他类型的移动机器人，类车机器人具有承重能力较强、行驶速度较快等优势，因此在制造、仓储等领域都具有十分广泛的应用[1].路径跟踪控制是类车机器人必须具备的一项关键技术，其作用是控制类车机器人沿着给定的参考路径行驶.由于机械机构相似，无人驾驶车辆的路径跟踪控制技术通常也可以用于类车机器人，然而类车机器人也具有一些迥异于无人驾驶车辆的特点，例如参考路径曲率幅度更大[7]、系统约束范围更小、零部件标准化程度更低，因此专门针对类车机器人路径跟踪控制的研究工作也受到了越来越多的重视.

针对类车机器人，研究者们已经提出了基于滚动优化控制[1]、反馈线性化控制[8]、滑模控制[9]、比例微分控制[10]、模糊控制[11]、强化学习控制[12]、深度学习控制[13]等控制方法的跟踪控制技术.这些研究工作具有积极意义，但是研究者们还未着重关注系统约束的影响.类车机器人与无人驾驶车辆具有相似的机械结构，所以同样受到前轮转角约束、前轮转角速度约束等系统约束的影响[14]，而且类车机器人的系统约束范围通常较小，受到的影响尤其显著[15].因此如果采用不考虑系统约束的控制方法，很容易导致类车机器人的路径跟踪控制出现误差过大乃至控制失效等问题.

在处理系统约束方面，模型预测控制（Model predictive control, MPC）具有引人瞩目的巨大优势.目前存在多种类型的MPC，如非线性MPC（Nonlinear MPC, NMPC）和线性MPC（Linear MPC, LMPC）等[16].NMPC通常具有多个预瞄点[17-18]，能够有效利用被控对象前方的参考路径信息[19]，因此具有较高的精确性，但是由于非线性优化求解计算成本较高，所以NMPC的实时性相对较差，虽然目前已有一些旨在优化NMPC实时性的研究工作[20-23]，但是优化后的NMPC实时性仍然远逊色于LMPC.与此同时，虽然LMPC的实时性较好，但是目前典型的LMPC大多采用无预瞄点的设计方法[24-34]，无法利用被控对象前方的参考路径信息[19]，因此其精确性相对较差.

针对现有模型预测控制方法难以同时兼顾精确性与实时性、其他控制方法难以在系统约束的影响下保障路径跟踪控制的精确性的技术现状，为实现同时具备高实时性与高精确性的类车机器人路径跟踪，以无预瞄点的LMPC为基础，引入基于逆运动学模型的前馈转向角信息，构建了包含误差预测模型和前轮转角预测模型的优化目标函数，提出了基于前馈模型预测控制（Feedforward MPC,FMPC）的类车机器人路径跟踪控制方法，该方法也是本文的主要创新之处.该控制方法通过MATLAB与Carsim联合仿真进行了验证，并与NMPC、LMPC、前馈控制、Stanley控制等路径跟踪控制方法进行了比较研究.

1 线性模型预测控制

目前类车机器人零件标准化程度较低，常采用非标轮胎作为驱动零件，轮胎力学参数较难获得，为保证控制方法的一般性，采用运动学模型作为路径跟踪控制的基础.类车机器人的运动学模型一般可以表示为

其中 ：x、y为全局坐标系中类车机器人后桥中心的横、纵坐标值，m；θ为全局坐标系中类车机器人的航向角，rad；v为类车机器人的纵向速度，m·s-1；δ为等效前轮转角，rad；l为类车机器人的轴距，m.

该模型可以抽象为

其中

取参考路径上距离类车机器人后桥中心最近的点作为参考点，在参考点对上述模型进行线性展开，可得

其中

其中，下标ref表示参考点信息，下标0表示当前状态.

考虑到迭代周期较短，因此模型状态量变化率约等于状态增量与迭代周期之比

其中，t表示t时刻，t-1表示t时刻之前1个迭代周期的时刻，表示t时刻的，T表示迭代周期.

联立(4)与(6)，可得预测模型

其中，t+1表示t时刻之后1个迭代周期的时刻，状态矩阵分别为

其中，I为单位矩阵.

预测时域内的所有迭代过程可以表示为

其中，i为迭代步数，i=1,2,···,p，c为控制步数，p为预测步数.

在(9)的迭代过程中，状态矩阵和的被假设不变，因此存在模型累积误差.为减小该累积误差的影响，在移动机器人、无人驾驶车辆等设备的路径跟踪控制中，通常将迭代周期和预测步数设为较小值，两者的乘积通常不足1 s.在如此短的时间内，模型状态矩阵的变化较小，累积误差的影响也会被有效减轻.

改写为矩阵形式可得

其中

使模型迭代获得的差分量平方和最小即可实现LMPC，因此可以将优化目标函数设计为

其中，Q为位姿误差权重矩阵.

将(10)代入(12)并转化为标准二次型

其中

加入系统约束，LMPC即相当于求解如下二次型

其中，下标lim 表示极限.

2 前馈模型预测控制

为了向LMPC控制器引入前馈信息，首先需要通过参考路径信息设定前馈转向角，因此路径规划系统生成参考路径时，必须给出每一个参考路径点处参考路径的曲率.

类车机器人的工作环境通常不需要考虑极端的动力学条件，因此可以假设类车机器人符合非完整约束，期望横摆角速度与行驶速度、参考路径曲率之间的关系为

其中，κ为曲率.

代入(1)并求逆函数，可得逆运动学模型

类车机器人跟踪的参考路径可能存在曲率突变，因此可以采用类车机器人前方参考路径点的期望前轮转角作为前馈信号，即

其中，下标pre表示预瞄点参数.

预瞄点与参考点之间的距离应满足

其中，d为预瞄距离，k为调节系数.

在此基础上，预测时域内的所有控制输入可以表示为

改写为矩阵形式可得

其中

其中，下标f表示前馈量.

前馈控制输入的优化目标函数可以设计为

其中

R为前馈信息权重矩阵.

将(21)代入(23)并转化为标准二次型

其中

将(26)与(13)合并

其中

其中，下标a表示总体量.

加入系统约束，前馈模型预测控制即相当于求解如下二次型

取求解(29)获得的控制序列中的第一个值作为实际的控制输入增量，与当前控制输入求和后，传递给类车机器人，即可实现类车机器人路径跟踪控制.

3 仿真结果

为测试提出的前馈模型预测控制算法的性能，通过MATLAB R2020a和Carsim 2019进行了联合仿真.仿真系统搭载于Dell G15 5510型计算机，其处理器为Intel(R) Core(TM) i5-10200H CPU@ 2.40 GHz.

仿真中类车机器人模型由Carsim提供，采用“DLC, Constant speed target”模板，模型参数如表1所示.对于 Carsim 的环境参数，“Driver controls”部分采用“Constant target speed”模式给定初始速度，“ Braking ”、 “ Shifting control” 和 “ Steering” 均空置， “ Start and stop conditions”部分采用“Run forever”模式.纵向速度由Carsim内嵌入的速度控制器控制，设置为3 m·s-1.类车机器人的约束条件主要设置了前轮转角约束和前轮转角速度约束.前轮转角约束设置为30°，即0.524 rad.类车机器人的转向机构通常采用功率较小的驱动机构，系统约束范围较小，因此前轮转角速度约束设置为15°·s-1，即0.262 rad·s-1.

表1 类车机器人模型参数Table 1 Parameters of car-like robot model

控制器基于MATLAB中的S-Function模块搭建，其参数如表2所示，为保证实时性，控制步数取较小值.

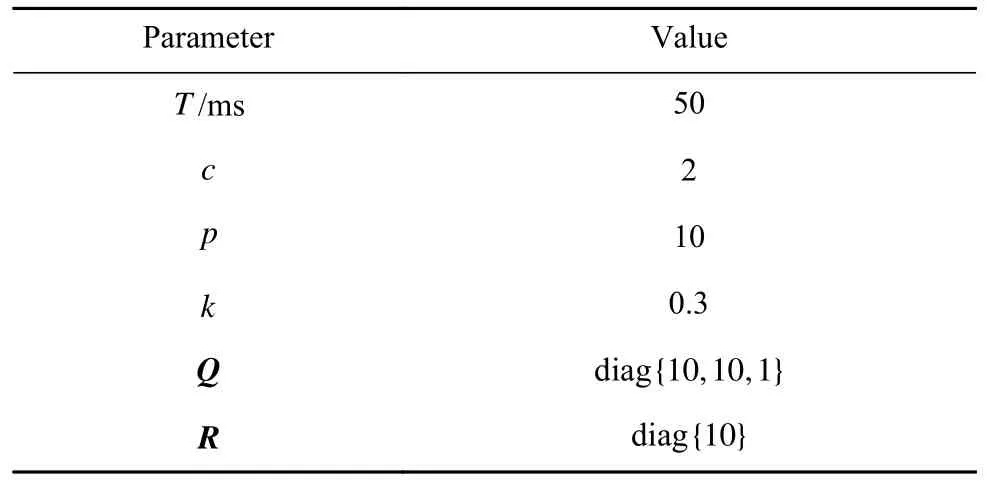
表2 前馈模型预测控制器参数Table 2 Parameters of the feed-forward model predictive controller

类车机器人常在较狭窄的环境下工作，参考路径曲率以及曲率突变幅度均较大.符合该特征的参考路径通常包含U型弯、四分之一圆弯道等，本文仿真中选择U型弯道作为参考路径，弯道曲率为0.2 m-1，即弯道半径为5 m.

为了较完备地测试前馈模型预测控制算法，设置了三组仿真.在第一组仿真中，前馈模型预测控制与其他模型预测控制方法进行了比较.在第二组仿真中，前馈模型预测控制与其他路径跟踪控制方法进行了比较.在第三组仿真中，在存在定位误差的工况下对前馈模型预测控制算法进了测试.

3.1 与其他模型预测控制方法的比较

在本组仿真中，前馈模型预测控制与线性模型预测控制、非线性模型预测控制进行了比较，三种控制方法在仿真结果中分别标注为FMPC、LMPC和NMPC，它们的参数均一致.

与其他模型预测控制方法的比较结果如图1至图7所示.图1所示为参考路径与类车机器人的行驶轨迹，前馈模型预测控制与非线性模型预测控制可以完成路径跟踪，线性模型预测控制在仿真开始后不久即控制失败.图2和图3分别显示了位移误差和航向误差，前馈模型预测控制器的位移误差最大绝对值为0.0648 m，航向误差最大绝对值为0.1091 rad，与非线性模型预测控制器的指标接近，线性模型预测控制的误差发散.图4和图5分别显示了前轮转角（Front wheel steering angle, FWSA）和前轮转角速度（FWSA speed, FWSAS），各模型预测控制器的所有控制变量均在系统约束范围内.

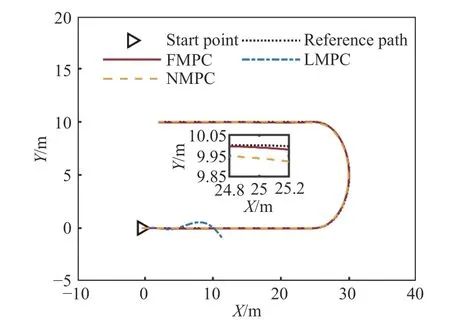
图1 几种模型预测控制器的仿真轨迹Fig.1 Simulation trajectories of several model predictive controllers

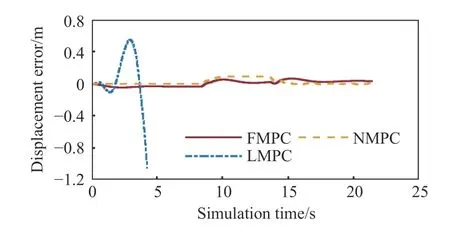
图2 几种模型预测控制器的位移误差Fig.2 Displacement errors of several model predictive controllers

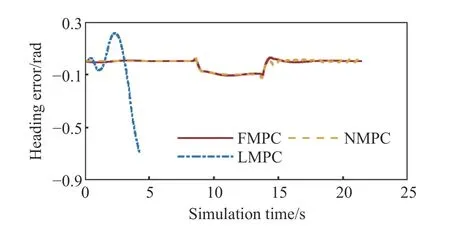
图3 几种模型预测控制器的航向误差Fig.3 Heading errors of several model predictive controllers

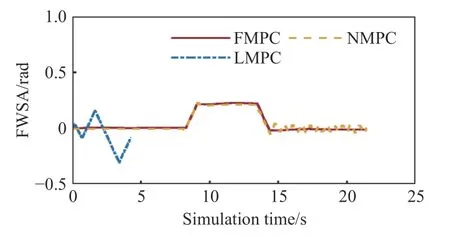
图4 几种模型预测控制器的前轮转角Fig.4 Front wheel steering angles of several model predictive controllers

图5 几种模型预测控制器的前轮转角速度Fig.5 Front wheel steering angle speeds of several model predictive controllers

在实时性方面，现有研究工作常采用每个控制周期内的解算时间及其统计值作为技术指标[20-23].图6和图7显示了实时性指标，即各模型预测控制器在每个控制周期内的解算时间和该指标的统计值，前馈模型预测控制在每个控制周期内解算时间的最大值为4.07 ms，平均值为2.66 ms，与线性模型预测控制的指标接近，非线性模型预测控制在每个控制周期内解算时间的最大值为21.07 ms，平均值为7.63 ms，前馈模型预测控制相比非线性模型预测控制将每个控制周期内解算时间的最大值减小了80.68%，平均值减小了65.14%.

图6 几种模型预测控制器的解算时间Fig.6 Time costs of several model predictive controllers

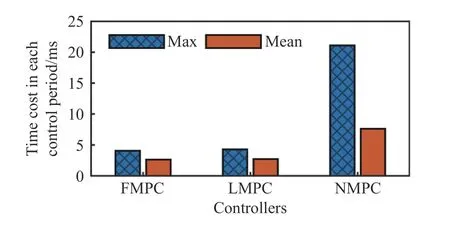
图7 几种模型预测控制器的解算时间统计值Fig.7 Time cost statistics of several model predictive controllers

3.2 与其他路径跟踪控制方法的比较

在本组仿真中，前馈模型预测控制与前馈（Feedforward）控制、Stanley控制进行了比较.前馈控制的控制量即式(17)的输出量.Stanley控制的比例系数设为-5.

与其他路径跟踪控制方法的比较结果如图8至图12所示.图8所示为参考路径与类车机器人的行驶轨迹，前馈控制与Stanley在弯道行驶的过程中先后控制失败.

图8 几种路径跟踪控制器的仿真轨迹Fig.8 Simulation trajectories of several path tracking controllers

图9和图10分别显示了位移误差和航向误差，前馈控制和Stanley控制的误差发散.图11显示了前轮转角，前馈控制的前轮转角在系统约束范围内，Stanley控制的前轮转角显著超出系统约束的范围.图12显示了前轮转角速度，前馈控制和Stanley控制的前轮转角速度均显著超出了系统约束的范围.超出系统约束即超出了转向系统的执行能力，前馈控制和Stanley控制给出的前轮转角和前轮转角速度超出系统约束是它们控制失效的主要原因.根据[15]可知，通过增加转向电机功率等方式可以减小系统约束的影响，但是会显著增加类车机器人硬件成本以及续航焦虑.前馈控制和Stanley控制均无需在线优化求解，实时性极为优越，与前馈模型预测控制没有可比性，故不再赘述.

图9 几种路径跟踪控制器的位移误差Fig.9 Displacement errors of several path-tracking controllers

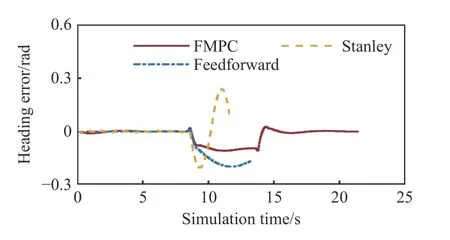
图10 几种路径跟踪控制器的航向误差Fig.10 Heading errors of several path-tracking controllers

图11 几种路径跟踪控制器的前轮转角Fig.11 Front wheel steering angles of several path tracking controllers

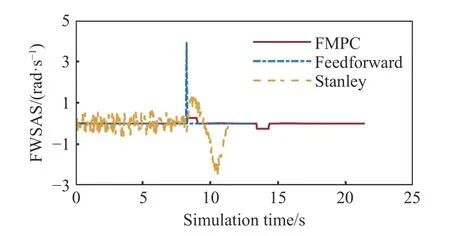
图12 几种路径跟踪控制器的前轮转角速度Fig.12 Front wheel steering angle speeds of several path tracking controllers

3.3 存在定位误差工况下的测试

为了进一步测试前馈模型预测控制在较恶劣环境下的性能，在仿真系统中加入了定位误差.该定位误差是指差分GPS（Global positioning system）等全局定位系统给出类车机器人位置时的系统误差.考虑到目前差分定位系统通常可以将定位误差保持在1 cm以内，故第一组仿真中在类车机器人的横坐标和纵坐标上分别加入了±1 cm的随机误差.为进一步测试极端工况下的性能，第二组仿真中在类车机器人的横坐标和纵坐标上分别加入了±5 cm的随机误差.

存在定位误差工况下的测试结果如图13至图19所示.第一组存在定位误差的仿真结果标记为1 cm，第二组标记为5 cm，作为对照组的是理想工况下的仿真结果，与3.1节中的前馈模型预测控制仿真结果一致，标记为Ideal.图13所示为参考路径与类车机器人的行驶轨迹.在存在定位误差的情况下，类车机器人仍然能够跟踪给定的参考路径，跟踪精度略低于理想工况下的跟踪精度.图14和图15分别显示了位移误差和航向误差.加入±1 cm定位误差后，前馈模型预测控制的位移误差最大绝对值和航向误差最大绝对值均有所增大，分别为0.0966 m和0.1177 rad，相对理想工况下的对应值分别增大了0.0318 m和0.0086 rad，增加幅度较小，与定位误差的最大绝对值接近.加入±5 cm定位误差后，前馈模型预测控制的位移误差最大绝对值和航向误差最大绝对值均有所增大，分别为0.1110 m和0.1144 rad，相对理想工况下的对应值分别增大了0.0462 m和0.0053 rad，增加幅度较小，与定位误差的最大绝对值接近.图16和图17分别显示了前轮转角和前轮转角速度，存在定位误差时，前馈模型预测控制的所有控制变量仍在系统约束范围内.

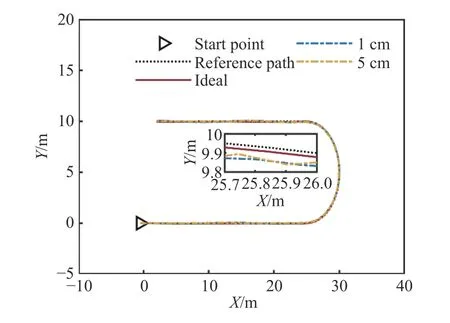
图13 存在定位误差的仿真轨迹Fig.13 Simulation trajectories with the localization errors

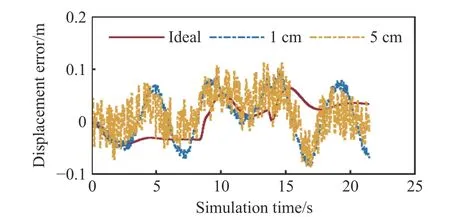
图14 存在定位误差的位移误差Fig.14 Displacement errors with the localization errors

图15 存在定位误差的航向误差Fig.15 Heading errors with the localization errors

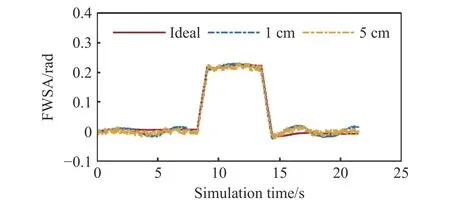
图16 存在定位误差的前轮转角Fig.16 Front wheel steering angles of several model predictive controllers

图17 存在定位误差的前轮转角速度Fig.17 Front wheel steering angle speeds of several model predictive controllers

图18和图19分别显示了存在定位误差时前馈模型预测控制的实时性指标，即在每个控制周期内的解算时间和该指标的统计值，解算时间的最大值、平均值与理想状态下的对应指标接近，因此可以认为定位误差对前馈模型预测控制的实时性无显著影响.

图18 存在定位误差的解算时间Fig.18 Time costs of several model predictive controllers

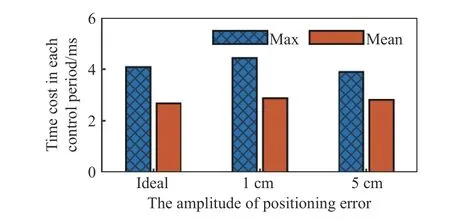
图19 存在定位误差的解算时间统计值Fig.19 Time cost statistics of several model predictive controllers

4 结论

针对模型预测控制方法以外的控制方法难以有效处理系统约束，难以在系统约束的影响下保障路径跟踪控制精确性，现有模型预测控制方法中非线性模型预测控制实时性差，线性模型预测控制精确性差的技术现状，为实现能够同时保障精确性和实时性的类车机器人路径跟踪，提出了基于前馈模型预测控制的控制方法.根据联合仿真结果，可以得到以下结论：

（1）本文提出的基于前馈模型预测控制的类车机器人路径跟踪控制器具有较高的精确性.在MATLAB和Carsim联合仿真结果中，位移误差最大绝对值为0.1110 m，航向误差的最大绝对值为0.1177 rad.在相同工况下，前馈模型预测控制与非线性模型预测控制的精确性接近，线性模型预测控制、前馈控制和Stanley控制的误差均发散.

（2）基于前馈模型预测控制的类车机器人路径跟踪控制器具有较好的实时性.在所有仿真结果中，控制器在每个控制周期内的解算时间最大值为4.31 ms.在相同工况下，前馈模型预测控制与线性模型预测控制的实时性相当，而且相比非线性模型预测控制，能够将每个控制周期内解算时间的最大值减小80.68%，平均值减小65.14%.

（3）基于前馈模型预测控制的类车机器人路径跟踪控制器能够将控制变量保持在系统约束范围内.在相同工况下，前馈控制的前轮转角速度、Stanley控制的前轮转角和前轮转角速度均超出了系统约束范围，因而导致了控制失效.

（4）基于前馈模型预测控制的类车机器人路径跟踪控制器受定位系统误差影响较小.在存在定位误差工况下的仿真结果中，位移误差、航向误差的增长幅度较小，与定位误差的幅值基本相当，每个控制周期内解算时间的最大值和平均值也未受到显著影响.

此外，与新兴的强化学习控制、深度学习控制相比，本文提出的前馈模型预测控制方法无需采集与辨识类车机器人参数，设计过程更加简单，具有较大的开发成本优势.