机理模型与集成学习混合驱动的机器人关节摩擦建模方法

2024-05-03邓金栋倪鹤鹏邹风山叶瑛歆

工程科学学报 2024年6期

邓金栋，倪鹤鹏，姬帅，梁亮，邹风山，叶瑛歆

1) 山东建筑大学机电工程学院，济南 250101 2) 山东大学机械工程学院，济南 250061 3) 沈阳新松机器人自动化股份有限公司，沈阳110180

机器人一体化关节通常由伺服电机、谐波减速器、编码器等组成，广泛应用于医疗、协作机器人等领域[1].实现机器人的高速、高精度及免力矩传感器柔顺控制，如拖动示教[2]、碰撞检测[3]、力位混合控制[4]等，需要建立准确的机器人动力学模型，而关节处的摩擦是影响动力学模型精度的关键因素[5].因此，建立准确的关节摩擦模型对于实现机器人高性能平滑控制至关重要.

伺服电机和谐波减速器是机器人关节中产生摩擦的主要单元.段书用等[6]采用Stribeck模型进行了谐波减速器的摩擦建模，该类静态摩擦模型能够较准确地描述混合润滑状态下摩擦力矩随转速增大而减小的特性，且易于辨识参数.LuGre模型[7-9]和GMS[10-11]模型也被应用于谐波减速器的摩擦建模，所构建的动态模型能够体现预滑动状态下的摩擦特性，然而待定参数众多，参数辨识难度大.针对谐波减速器摩擦力矩存在的周期波动特征，部分学者采用傅里叶级数模型[12-14]对波动摩擦力矩进行了建模.然而，以上方法多采用恒定的幅值和相位参数，未考虑谐波减速器速度变化对力矩波动幅频特性的影响，限制了最终模型的精度.

负载是导致关节摩擦力矩呈现复杂非线性特性的另一重要因素.Madsen等[15]与Gao等[16]建立了关节摩擦力矩与负载间的非线性映射模型，模型精度相对于线性模型有所提高，但仅体现了负载与库伦摩擦力矩的关系，难以完整表征负载变化对摩擦力矩的影响规律.石崟等[17]指出负载对库伦摩擦力矩以及黏性摩擦力矩均会产生影响，并通过经验公式描述了负载与黏性摩擦力矩的关系，但模型结构复杂，存在黏温、黏压等众多未知参数，辨识难度大，且对模型精度的提升有限.

以上考虑各类影响因素的关节摩擦机理建模方法，能够保证模型参数具有一定的物理意义，便于分析特性的演变规律.然而，由于建模过程中存在对真实系统的简化和假设，如线性化和忽略高阶项等，模型误差必然存在.同时，通过增加机理模型复杂度来提高准确性的方式，不仅对模型精度的提升有限，而且显著增大了参数辨识的难度.

近年来，具有强大非线性拟合能力的数据模型受到广泛关注[18-21]，部分学者结合传统机理模型与数据模型，并应用到机器人关节摩擦建模中.张铁等[22]认为机理模型误差主要源于摩擦力矩的波动，因此采用Back propagation (BP)神经网络模型补偿傅里叶级数模型对波动摩擦力矩的建模误差.贺苗等[23]仅考虑速度对摩擦力矩的影响，引入Radial basis function (RBF)神经网络，补偿了机理模型的建模误差.然而，以上混合驱动建模方法对关节摩擦特性的影响因素考虑不全面，虽简化了机理模型结构和参数辨识过程，但增大了数据模型的拟合难度，精度提升有限.同时，以上方法均采用单个神经网络模型做误差补偿，面对具有不同特性的机器人关节，容易出现欠拟合或过拟合现象，鲁棒性不强.

针对以上问题，本文提出了一种机理模型与集成学习混合驱动的机器人关节摩擦建模方法.首先，综合考虑转速、负载对关节摩擦特性的影响及其周期波动特性，基于经验知识与物理规律分别建立伺服电机与谐波减速器的参数化摩擦模型，进而构建机器人关节的整体参数化摩擦机理模型.然后，针对摩擦机理模型的计算残差，提出基于eXtreme gradient boosting (XGBoost)方法建立数据驱动的残差补偿模型.XGBoost是一种采用boosting集成模式的集成学习方法，以分类与回归树(Classification and regression tree, CART)为基学习器，通过迭代增加CART共同构建强学习器.相比于单个神经网络模型，多CART集成的结构使得XGBoost模型具有更好的泛化能力和鲁棒性，且在表格数据的特征提取和预测方面，性能优于深度神经网络，适合本文对机理模型残差的建模.最后，基于关节摩擦力矩测量实验台及工业机器人，通过对比实验，验证了所提出的混合驱动的机器人关节摩擦建模方法的有效性.

1 机理与数据混合驱动的机器人关节摩擦模型总体结构

机理与数据混合驱动的机器人关节摩擦模型的总体结构如图1所示.模型的输入u包括机器人关节的电机角位置、转速和负载力矩参数，输出为预测的关节摩擦转矩Tf*.

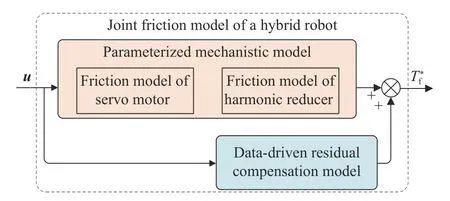
图1 混合驱动的机器人关节摩擦模型Fig.1 Joint friction model of a hybrid robot

伺服电机和谐波减速器是关节中产生摩擦的主要原件.因此，基于先验知识和物理规律，机理模型包含了伺服电机和谐波减速器的参数化模型，是整体关节摩擦模型的基础单元.建模过程需考虑影响伺服电机和谐波减速器摩擦特性的诸多因素，但过于复杂的模型结构对计算精度的提升有限，且增大了参数辨识的难度.因此，本文综合考虑了转速、谐波减速器的齿间啮合作用及负载力矩等影响摩擦特性的主要因素，建立了简化的参数化摩擦机理模型.

由于线性假设和模型简化，机理模型的未建模部分具有强非线性，因此，采用数据驱动模型补偿机理模型的非线性残差.为提高补偿精度，需考虑两方面的问题.首先，模型结构是影响建模精度的关键因素，应具备强非线性特征提取能力，以满足拟合精度的要求.然后，模型超参数的选择是影响精度的另一关键因素.对此，本文提出了基于集成学习的残差补偿模型建模方法，同时采用贝叶斯优化的方法进行模型超参数寻优，保证模型的精度和鲁棒性.

2 机器人关节摩擦机理模型建模

建立机器人关节的动力学模型如式（1）所示：

其中，Tm为伺服电机的输出力矩,Jm为电机轴与波发生器的转动惯量,Jl为关节输出端法兰的转动惯量，N为减速比，θ为电机轴角位置,Tf为关节摩擦力矩，Tload为关节输出端的负载力矩.伺服电机和谐波减速器是产生摩擦的主要单元，因此Tf可表示为：

其中，Tmf为电机摩擦力矩，Trf为谐波减速器摩擦力矩.本章基于机器人关节的传动原理，分析转速、谐波减速器齿间啮合及负载对摩擦的影响机制，并建立其参数化机理模型.

2.1 转速对摩擦特性的影响分析与建模

转速是影响伺服电机和谐波减速器摩擦的关键因素.伺服电机结构简单，不存在齿啮合过程，摩擦力较小.因此，采用库伦-黏性模型[24]对电机摩擦进行建模.一定转速下，其摩擦力矩可描述为：

其中，Tmc为电机库伦摩擦力矩， σm为电机黏性摩擦系数，ω为电机的角速度，sgn(·)表示符号函数.

相较于伺服电机，谐波减速器结构复杂，存在齿啮合过程，具有更复杂的摩擦特性.由现有研究可知[25]混合润滑状态下，其摩擦力矩会随转速的增大而减小，这是由于刚轮与柔轮啮合齿间的润滑膜厚度随着转速的增大而增大，减小了啮合齿的接触面积，导致摩擦力矩减小；充分润滑状态下，啮合齿间被润滑膜全部充满，摩擦力矩主要由润滑油的流动速度和黏度决定，并随润滑油流动速度的增大而增大.因此，本文采用Stribeck模型描述不同转速下的摩擦力矩，如下所示：

其中，Trc为库伦摩擦力矩，Ts为最大静摩擦力矩， ωs为Stribeck速度， σr为谐波减速器黏性摩擦系数.

2.2 谐波减速器波动摩擦力矩建模

由于谐波减速器柔轮与刚轮齿的周期啮合作用，其摩擦力矩呈现出周期性波动现象.如图2所示，零差云控eRob80型机器人关节，空载状态下电机指令转速为50 rad·min-1(ωr=0.833 Hz)时，采集到的电机输出力矩如图3(a)所示，即摩擦力矩具有明显的周期波动性.对摩擦力矩信号进行快速傅里叶变换(FFT)，频率特征如图3(b)所示.摩擦力矩包含的频率分量主要有：谐波减速器输入转动频率ωr的一次谐波(0.833 Hz)、二次谐波(1.667 Hz)、五次谐波(4.167 Hz)、十次谐波(8.333 Hz).

图2 零差云控eRob80型机器人关节Fig.2 Zero difference cloud control eRob80 robot joint

图3 机器人关节波动摩擦力矩及其频谱分析.(a) 波动摩擦力矩; (b) 波动摩擦力矩主要频率成分Fig.3 Fluctuating friction torque of the robot joint and its spectrum analysis: (a) fluctuating friction torque; (b) main frequency components of the fluctuating friction torque

对比现有研究结果可知[12,22]，由于谐波减速器制造精度的差异性，个体间呈现出不同的摩擦力矩波动特性.虽然主要谐波成分与输入转动频率均呈现倍数关系，但其个数和倍数的大小是不确定的.因此，采用傅里叶级数对摩擦力矩的波动部分Trfp进行建模，如公式5所示，其中cj、bj为每一项多项式的幅值.

由于波动的主要谐波成分集中在低频段，高频成分幅值较小，可忽略不计.因此J可取10.对式(5)进行简化，可建立以电机角度θ为自变量的波动摩擦模型

其中，θ为电机角度，Aj和φj分别为波动摩擦力矩的幅值和相位.

2.3 负载对摩擦特性的影响分析与建模

负载主要影响谐波减速器的接触摩擦力，对伺服电机摩擦影响较小.接触摩擦力与接触表面之间的法向载荷有关，在关节末端施加负载力矩时，增大了啮合齿对间的法向载荷，同时柔轮在法向载荷的作用下会发生弹性变形[26]，导致刚轮和柔轮的啮合齿对数增加，进一步影响摩擦特性.负载对谐波减速器的最大静摩擦、库伦摩擦和黏性摩擦均有影响[17]，且对库伦摩擦影响较大，呈现幂函数变化规律.若同时考虑负载对最大静摩擦、库伦摩擦和黏性摩擦的影响，则最终的参数化机理摩擦模型过于复杂，容易降低参数辨识的精度，同时对模型整体精度的提升不大.因此，本文主要考虑负载对库伦摩擦力矩的影响，建立如式（7）所示的简化参数化模型：

其中，Trfτ为负载引发的库伦摩擦力矩增量，a为负载力矩系数，λ为负载指数参数.

2.4 机器人关节摩擦综合参数化模型

综合考虑转速、负载对伺服电机和谐波减速器摩擦特性的影响及其周期波动特性，可建立伺服电机、谐波减速器及机器人关节的综合摩擦模型，如下所示：

3 数据驱动的残差补偿模型建模

机理模型虽考虑了影响关节摩擦的多种因素，但建模过程中线性假设和模型简化不可避免，降低了模型的精度.针对机理模型计算存在的非线性残差，本章建立了基于集成学习的残差补偿模型，同时采用贝叶斯优化方法进行模型超参数寻优，以提高模型精度和鲁棒性.

3.1 基于集成学习的残差补偿模型

已有学者将深度神经网络(Deep neural networks,DNN)应用到机器人关节摩擦建模中，大多采用单一神经网络模型方法.然而，单一网络模型具有有限的非线性拟合能力，不合理的模型结构及超参数容易导致模型过拟合或欠拟合.相比而言，集成学习方法[27-28]通过组合多个简单的弱学习器以构建强学习器，常用的基学习器包括迭代二叉树(ID3)、分类与回归树(CART)等，模型集成策略及训练机制能够有效地提高模型的泛化能力和鲁棒性.集成学习方法有三种基本模式，即Bagging、Boosting和Stacking.如图4所示，Boosting模式通过迭代使用弱学习器来补偿上一个模型的预测残差，最终各弱学习器的预测结果被加权作为模型的整体输出，能够有效地提高整体模型的预测精度.因此，本文采用Boosting模式构建残差补偿模型.在实际应用Boosting集成学习模型时，根据已有的数据资源和所针对的问题构造训练数据集，并通过特征重要性分析、数据滤波、数据标准化等数据处理方法，增强训练数据的可靠性，提高模型精度.

图4 Boosting集成学习模式Fig.4 Ensemble learning in the boosting mode

XGBoost[29-30]是一种基于分类与回归树的Boosting集成学习模型，用于解决分类和回归问题，其模型结构如图5所示.相比于DNN，XGBoost在摩擦特性建模方面具有以下优势：首先，摩擦力矩残差及其预测所依据的电机转速、角度、力矩等数据共同构建的数据集被称为表格数据[31].相较于DNN，XGBoost已经被证明在处理表格数据方面具有更优异的性能.事实上，DNN模型通过时空建模以捕捉高维特征，更擅长处理图像、自然语言等问题.其次，XGBoost采用了核外计算机制，对计算资源要求低，能够允许用户在普通计算机处理数亿样本数据，训练时间远小于DNN模型，更适合部署在机器人控制器端.因此，本文提出采用XGBoost构建摩擦力矩的残差补偿模型.

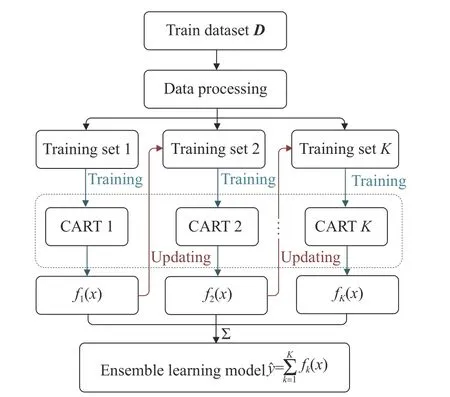
图5 XGBoost模型网络结构Fig.5 Structure of the XGBoost model

XGBoost的基本原理如下：对于给定的数据集D={(xi,yi)}(|D|=n,x∈Rp,y∈R)，其中xi为第i个样本的特征向量，yi是对应的标签，即真实值，n与m分别表示样本数及特征数，XGBoost模型可表示为：

其中xi为输入数据，为预测值，K为XGBoost模型中的CART数量，fk(xi)为第k棵树对xi的预测值，F={f(x)=ωq(x)}(q:Rp→T,ω∈RT)表示CART的函数空间，q为每棵树结构，T为叶节点数量，每个fk都对应一个独立的树结构q和叶权重ω.XGBoost通过最小化如下正则化目标函数来建立K棵树结构：

XGBoost通过迭代添加树的方式实现训练，第t次迭代时第i个样本的预测值可表示为

其中，为第t-1次迭代的预测值.此时，目标函数可表示为

为快速优化目标，使用二阶泰勒展开对式 (14)进行近似处理，如式（15）所示

定义Ij={i|q(xi)=j}为叶节点j的样本集，去除式 (15)中的常数项，并展开正则项，目标函数可重写为：

理想情况下，最优权值ω*j可表示为

因此，式 (16)可写为：

至此，式(18)可作为CART结构的评价函数，数值越小，则表示树结构越好.然后，采用贪心算法[29]对树进行分支，从单个叶节点开始迭代，最终形成树结构.

本文所构建的XGBoost模型，训练数据集D的输入包含采集到的电机角速度ω、电机角度θ和负载力矩Tl，即式(10)对应的模型自变量，输出为采集到的摩擦力矩与式(10)计算力矩之间的差值，即残差力矩，模型所采用的基学习器为CART.为提高网络模型预测精度，需要对训练数据集D进行数据处理，首先计算各特征平均覆盖度(cover)，分析各特征对标签的重要性，然后采用高斯低通滤波方法对其进行滤波处理，减少原始数据中的不确定因素，最后对其进行数据归一化.

3.2 基于贝叶斯优化的超参数寻优

超参数是影响模型精度和训练效率的重要因素.超参数寻优即寻找一组使模型具有良好性能的超参数，可表示为：

其中ϕ为超参数集， Δϕ为最优化目标函数， Ψ为超参数的取值范围， ϕ*为寻优获得的超参数集.XGBoost模型的待优化超参数如表1所示.

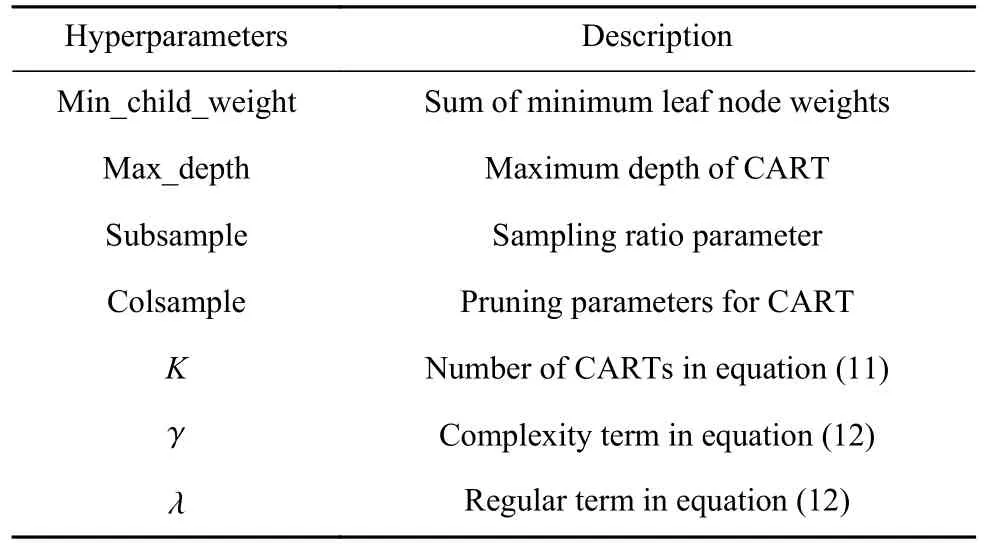
表1 XGBoost模型的待优化超参数Table 1 Hyperparameters to be optimized for the XGBoost model

在常规的参数优化中，目标函数往往具有显式的数学表达形式.然而，在超参数优化中， Δϕ是黑箱目标函数，增大了寻优难度.网格搜索和随机搜索是解决黑箱目标函数寻优的常用方法，但搜索效率较低，容易陷入局部最优.贝叶斯优化[32]是一种基于概率分布的全局最优化算法，首先基于假设的先验分布，在获得后验分布后修改原分布置信度，能够从黑箱目标函数中获取信息，迭代地找到下一个评估位置以逼近最优解，收敛速度快.因此，本文选择贝叶斯优化方法进行超参数寻优.

概率代理模型和采集函数是贝叶斯优化的两个核心部分[33].贝叶斯优化通过有限的样本点构造概率代理模型，以近似代替黑箱目标函数，降低计算目标函数的成本.常用的概率代理模型包括高斯过程模型和随机森林.采集函数将输入空间、观测空间和超参数空间映射到实数空间，并产生下一个待评估的观测点.常用的采集函数包括Expected improvement (EI)[34]、Probability of improvement (PI)[35]、Upper bound confidence (UCB)[36]等.采用贝叶斯优化方法进行模型超参数寻优时，模型输入为图5所示的训练数据集D和XGBoost模型，输出为表1所示的XGBoost模型超参数集，利用高斯过程构建概率代理模型，确定待优化超参数集的先验分布，并基于EI采集函数确定概率代理模型的最优取值点，具体优化过程如下：

Hyperparameter optimization process D={(xi,yi)}XGB(xi)=K∑Input: Sample Dataset ; XGBoost model fk(xi)k=1 Output: Optimal hyperparameter set ϕ*Ψ 1 Determine the search space for hyperparameter sets ;2 Initializing the Gaussian process model;3 for t=1,2,3,···, do 4 Optimizing the collection function to obtain the next evaluation point ϕt Δϕt 5 Calculate objective function ;{ϕt,Δϕt}6 With Update Collection Function Dataset;7 Updating the Gaussian process Model;8 End for

4 实验验证

4.1 实验环境与方案

搭建如图6所示的摩擦力矩测量实验台，采集eRob80型机器人关节在不同电机位置、速度及负载下的摩擦力矩.加载伺服电机和行星减速器为测试关节提供负载力矩，可提供[0 , 20] N·m的动态力矩.实际施加在关节输出端的负载力矩由动态扭矩传感器测量，测量精度为0.01 N·m.摩擦力矩、速度、角位置和负载力矩的采样频率均为1 kHz.

图6 机器人关节摩擦力矩实验台Fig.6 Friction torque measurement device for the robot joint

由式(1)可知，匀速状态下折合到电机端的关节整体摩擦力矩Tf可由电机输出力矩与负载力矩求得：

实验环境温度为25 ℃，选取的实验参数如表2所示，在关节低速状态下具有较小的速度间隔，以观察Stribeck现象.同时采用傅里叶级数构造关节输入轨迹[22]并施加动态扭矩，测量对应的摩擦力矩.为了减小测量误差，每个实验重复进行三次，测量结果取平均值，同时采用高斯低通滤波器对测量数据进行滤波处理.

表2 实验参数设置Table 2 Experimental parameter settings

4.2 机理模型的参数辨识

机理模型的参数辨识分两步进行：首先，按照设定的各速度值，测量关节空载状态下的摩擦力矩，此时与负载相关的摩擦力矩部分为零，进而辨识式(3)～(4)及(6)中的未知参数；然后，按照各测量点设定的负载力矩，对关节进行加载实验，获得不同负载下的摩擦力矩，辨识式(7)中的未知参数.

关节空载状态下，平均摩擦力矩随电机转速的变化如图7所示.转速小于40π rad·min-1时，平均摩擦力矩随转速的增大而减小，呈现出明显的Stribeck现象.转速大于40π rad·min-1时，平均摩擦力矩随转速的增大而增大.采用最小二乘方法对式(3)～(4)、(6)内的未知参数进行辨识，辨识结果如表3所示.由图7可知，所建立的机理摩擦模型能够较准确地描述Stribeck现象，但由于黏性摩擦力矩与润滑油流动速度间的线性假设，忽略了润滑状态的变化，使得模型在400π～800π rad·min-1阶段的精度较差.

表3 参数辨识结果Table 3 Parameter determination results

图7 空载、不同转速下的平均摩擦力矩与机理模型拟合结果Fig.7 Fitting results of mean friction torque and mechanistic model under no-load and different motor speeds

不同电机转速下，关节末端施加不同负载扭矩，平均摩擦力矩的变化如图8所示，呈现幂函数变化趋势.辨识式(6)中的未知参数，可得a=0.0575，λ=1.52.

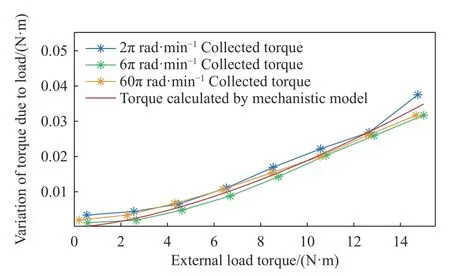
图8 不同转速和负载力矩下的实际平均摩擦力矩与机理模型计算结果Fig.8 Mean of actual friction torque and torque calculated by the mechanistic model under different motor speeds and load torques

4.3 混合驱动摩擦模型的性能验证

本节通过匀速加载实验及机器人动态跟踪实验验证所构建的混合驱动模型的有效性，并与现有方法进行对比，测试模型精度.在电机转速为600π rad·min-1、负载扭矩为8 N·m的条件下，摩擦力矩的测量和不同建模方法的计算结果如图9所示.

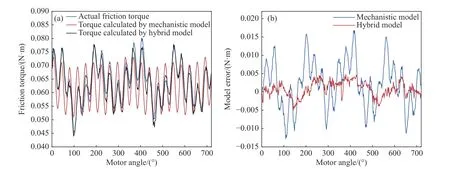
图9 600π rad·min-1、8 N·m负载下的实际摩擦力矩、模型计算力矩及模型误差.(a) 实际摩擦力矩与模型计算力矩; (b) 模型误差Fig.9 Actual friction torque, torque calculated by the model, and model error under 600π rad·min-1 and 8 N·m load: (a) actual friction torque and torque calculated by the model; (b) model error

由图7可知，机理模型在600π rad·min-1时具有较大的平均摩擦力矩误差.加入基于集成学习的残差补偿模型后，在平均摩擦力矩和波动力矩方面精度提升明显.如表4所示，峰值误差、平均误差和均方根误差分别减小了70.4%、65.1%、66%.

表4 匀速加载实验下的模型精度比较Table 4 Comparison of model accuracy under the uniform loading experiment

如图10所示，将实验使用的eRob80型关节安装到水平关节机器人作为第一个关节，基于傅里叶级数构造关节1的运动轨迹，如图11所示.实验过程关节2保持不动，采用基于PC的控制器实现关节1的运动控制和数据采集.

图10 水平关节机器人Fig.10 Horizontal robot joint

图11 关节1运动轨迹Fig.11 Joint 1 motion trajectory

建立水平关节机器人的动力学模型，关节的负载力矩可由动力学模型计算获得.基于机器人动力学模型和关节摩擦模型，对关节1电机力矩进行预测，不同摩擦建模方法的预测结果如图12所示.由图可知，本文所提出的混合驱动模型具有更高的预测精度和稳定性.如表5所示，相比于机理模型，本文混合驱动模型峰值误差减小了53.1%，平均误差减小了65.5%，均方根误差减小了62.9%.

表5 基于不同模型预测的电机力矩误差Table 5 Motor torque error predicted based on different models

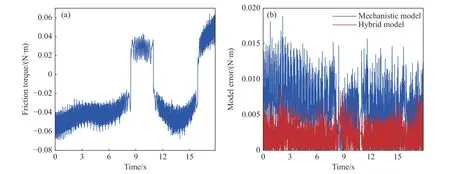
图12 实际电机力矩与模型误差.(a) 实际电机力矩; (b) 基于不同摩擦模型预测的电机驱动力矩误差Fig.12 Actual motor torque and model error: (a) actual motor torque; (b) errors of motor torque prediction based on different friction models.

采用反向传播神经网络(BP)、支持向量机(SVM)、卷积神经网络(CNN)和长短时记忆神经网络(LSTM)方法建立残差补偿模型，同时结合机理模型构建不同的混合驱动模型进行对比实验，不同混合驱动模型的误差对比如图13所示.由表5可知，相比于其他混合驱动模型，本文模型在峰值误差、平均误差和均方根误差方面具有更小的模型误差，表明XGBoost模型具有更好的特征提取和非线性拟合能力，更适应于摩擦建模.

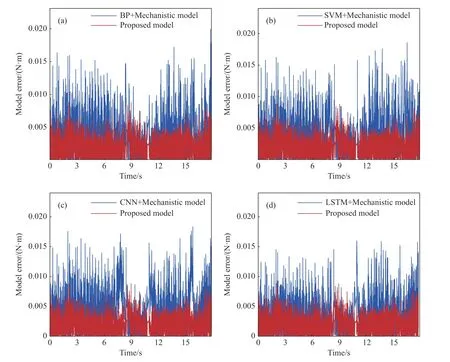
图13 基于不同混合驱动模型预测的电机力矩误差.(a) BP+机理模型与本文模型误差; (b) SVM+机理模型与本文模型误差; (c) CNN+机理模型与本文模型误差; (d) LSTM+机理模型与本文模型误差Fig.13 Errors of motor torque prediction based on different hybrid models: (a) error between the BP + mechanistic model and the proposed model;(b) error between the SVM + mechanistic model and the proposed model; (c) error between the CNN + mechanistic model and the proposed model;(d) error between the LSTM + mechanistic model and the proposed model