单绳缠绕式矿井提升机制动瞬态冲击抑制策略

解辉 沈刚 刘东 汤裕 朱真才

（1.中国矿业大学 机电工程学院，江苏 徐州 221000；2.安徽理工大学 机电工程学院，安徽 淮南 232000；3.中国船舶集团有限公司 第七一三研究所，河南 郑州 450015）

矿井提升机作为煤炭生产中的关键设备，承担着矿物提升、材料和设备的运输任务，而制动系统作为提升机最后一道也是最为关键的安全保障设备，其运行安全性对全矿的生产乃至人员的生命安全都有重要影响［1］。矿井提升机制动系统可以归纳为阀控液压缸系统，其工作过程为松闸-贴闸-压紧。目前，一些常见的控制方法，例如PID［2］、模糊控制［3］和自适应控制［4］已经应用于矿井提升机制动系统。然而，上述控制方案将制动器工作过程的控制模式设定为制动力闭环，制动系统的弹性刚度系数在闸瓦接触到闸盘前后存在从零到一个很大值的跳变，从而引起系统的结构跳变，进而导致制动力冲击现象，造成制动安全性下降。

目前，针对矿井提升机制动瞬态冲击的研究尚缺乏，但从现有的研究发现，制动控制系统的反馈增益是影响制动瞬态冲击的关键因素，通过选择较小的反馈增益可以在一定程度上抑制制动力冲击问题。但在煤矿安全规程中对制动器贴闸时间有严格要求，较小的反馈增益会造成贴闸时间延长，导致贴闸时间不满足安全规程要求，影响制动安全。为解决这一问题，将制动过程进行分段控制，贴闸段采用位置闭环控制，贴闸完成后稳态切换至制动力闭环控制。采用这种分段控制策略，不仅可以解决传统全程力闭环控制策略导致的瞬态冲击问题，而且可以通过设计合理的贴闸轨迹来实现缩短贴闸时间的目的，进而提高制动安全性。当前，对于模式切换控制方法，相关学者已经开展了一些研究，提出了鲁棒控制［5］、阻抗控制［6-7］、动态混合力位控制［8-9］等。鲁棒控制在解决控制系统参数不确定性和外部扰动问题方面具有优势，在一定程度上能够提高被控系统的稳定性和鲁棒性。文献［10］中针对不确定切换系统，提出了一种能够在任意时变切换规则下的鲁棒积分滑膜控制方法，实现了存在不匹配不确定性的切换系统的稳态控制。但本文所研究的制动系统在制动器闸瓦与闸盘贴合前后会存在外负载刚度参数跳变的问题，对于这种情况，采用常规的鲁棒控制方法难以获得令人满意的控制性能。阻抗控制作为一种典型多模式切换控制策略，主要用于终端工作与其环境之间的安全交互。文献［11］中针对机器人与环境的安全交换控制，提出了一种基于近似动态逆变的保稳变阻抗控制办法，保证了所需可变阻抗动力学的指数稳定性。然而，由于制动系统对贴闸时间的性能要求以及闸瓦的大刚度的固有特性，导致阻抗控制方法难以应用于制动系统。混合力/位置控制的设计问题涉及如何保证不同控制器在每个切换瞬间的稳定性，以及随动态特性的变化保证跟踪性能的准确性。因此，混合力/位置控制更适合应用于制动系统的切换控制。

在制动系统中进行混合力位控制时不可避免地面临着非线性摩擦、外部扰动和建模不确定性。以上这些不确定因素可能会使混合控制系统出现极限循环、抖振和低控制精度等问题。针对以上问题，文献［12］中设计了一种变结构控制器，在一定程度上解决了参数不确定性和系统随机扰动等问题。文献［13］中综合考虑了系统中参数和外界扰动的不确定性，提出了一类带有非线性扰动不确定切换系统的鲁棒控制。但对于参数发生较大跳变的制动系统，采用常规的适用于参数慢时变的控制方法，系统很难获得较高的跟踪性能。快速终端滑模控制方法具有使系统在有限时间内收敛为零的特点，被广泛应用于需要快速响应的被控对象［14-15］。

此外，安全制动是保障提升机在遇到紧急情况下的重要环节，为了提高制动的安全性，需要尽量减小制动器的贴闸时间。然而，实际的机电液系统都受着各种运动学和动力学约束，例如速度约束和控制输入饱和，这导致贴闸时间不可能无限地减小。因此，在系统压力和流量的约束条件下尽可能减小贴闸时间是本文所要解决的重要问题，该问题通常被称为最小时间轨迹规划。目前，关于最小时间轨迹规划问题的几个典型方法包括基于速度极限曲线的数值积分法、多面体方法、双向检查法以及非线性滤波器法［16］。文献［17］中将约束轨迹规划与非线性运动控制相结合，实现了电液执行器在约束条件下的精确轨迹跟踪。

受以上文献启发，本文提出了一种混合贴闸/压紧控制策略，用于单绳缠绕式矿井提升机制动系统的安全制动控制。首先，将制动控制过程划分为贴闸和压紧控制。然后，基于滞回切换原理，提出了制动系统贴闸/压紧混合控制策略，实现了贴闸与压紧控制的稳态切换，抑制了制动瞬态冲击。最后，设计了一种基于终端滑模的内外双闭环最小时间贴闸控制策略，不但可以使制动系统在满足流量和压力约束条件下实现最短时间贴闸，而且保证了制动器贴闸轨迹精准跟踪。

1 制动系统建模与问题提出

1.1 制动系统建模

如图1所示为矿井提升机的电液制动系统原理图，该系统主要由制动器、伺服阀、闸瓦、闸盘、位移及压力传感器等组成。当系统接收到制动命令时，制动器由伺服阀控制推动闸瓦形成作用于闸盘上的制动正压力，进而使得卷筒减速，最终达到提升系统减速的目的。

图1 阀控电液制动系统基本原理图Fig.1 Schematic diagram of valve controlled electro-hydraulic braking system

本文将活塞、活塞杆以及闸瓦等活动部件等效为质量为m的质量块进行受力分析。盘式制动器在接收到制动命令后经历施闸、压紧两个阶段，在施闸阶段，盘式制动器主要克服非线性摩擦力，在压紧阶段，盘式制动器主要完成期望的制动正压力。根据牛顿第二定律，盘式制动器负载力平衡方程为

式中，B为黏性摩擦系数；为基于Stribeck效应的摩擦模型，=a1tanh+a2tanh-a2tanh；a1和a2为不同摩擦力的幅值；b1、b2和b3为摩擦模型系数，用以近似描述各种摩擦效应；Fz(t)=sqkf(xp-x0)；x0为闸盘的位置。如图1所示，此时闸瓦受到位移约束，一般选择x0=0；sq为二进制变量，可以描述为

式中，kf为制动器刚度系数。为简化建模，本文未考虑环境接触的恢复系数与结构阻尼等因素。

考虑制动器的内泄漏与油液压缩性，制动器流量连续性方程可以写为

式中：QL为负载流量；Ap为制动器有效作用面积；Ct为制动器内泄漏系数；pL为制动器负载压降，pL=p1-p2；Vt=V1+V2为制动器油腔总容积，其中V1=V0+Apxp，V2=V0-Apxp，V0为制动器活塞处于中位时两腔容积；βe为液压油的有效体积弹性模量。

根据流体传动理论，制动系统伺服阀流量方程可以表示为

式中：Cd、wv和xv分别为伺服阀的流量系数、节流口面积梯度和阀芯位移，其中阀芯位移可以表示为xv=kvu，kv为伺服阀的电气增益，u为伺服阀控制电压；ps为系统供油压力；ρ为液压油密度；pL为负载压力；sign(·)为符号函数。

本文中研究的矿井提升机制动瞬态冲击抑制控制方法均是基于制动系统模型进行设计的，因此需要将上文所建立的制动系统模型转化为状态方程的形式。根据制动系统负载力平衡方程和流量连续性方程，系统状态方程可以表示如下：

为解决制动瞬态冲击问题，本文将盘式制动器贴闸与压紧两个动作的控制设计为位置/力混合控制模式。因此，混合贴闸/压紧动态制动系统状态方程表示如下：

1.2 控制问题提出

本文的控制目标是实现矿井提升机的制动瞬态冲击抑制，减小贴闸时间，提高制动的安全性。因此，本文的控制问题可以归纳如下：

（1）设计制动系统的贴闸/压紧混合控制策略，实现由贴闸控制到压紧控制的稳态切换，抑制制动瞬态冲击；

（2）设计一种最速贴闸控制器，可以使得制动系统在满足流量和压力约束条件下以最短时间完成贴闸动作，减小制动器空动时间。

2 混合贴闸/压紧控制策略

如图2所示为矿井提升机制动瞬态冲击抑制控制方案。闸瓦位置控制器主要实现制动器的快速贴闸；压紧控制器主要用于闸瓦与闸盘贴合后的制动力跟踪；自主切换策略主要实现盘式制动器由位置控制到力控制的自主稳态切换，以减小切换过程中存在的制动力冲击。

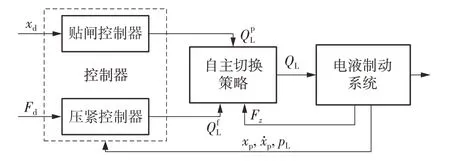
图2 混合贴闸/压紧控制策略方案Fig.2 Hybrid shoe-approaching and braking control strategy

如图3所示为混合贴闸/压紧控制器的基本工作原理，具体详细的切换规则设计过程将在后续的文章介绍。混合控制器的切换触发条件由切换变量τ决定，该变量主要由闸瓦与闸盘接触后的制动力Fz决定，ϑ为阈值。混合贴闸/压紧控制系统的最终控制律定义如下：

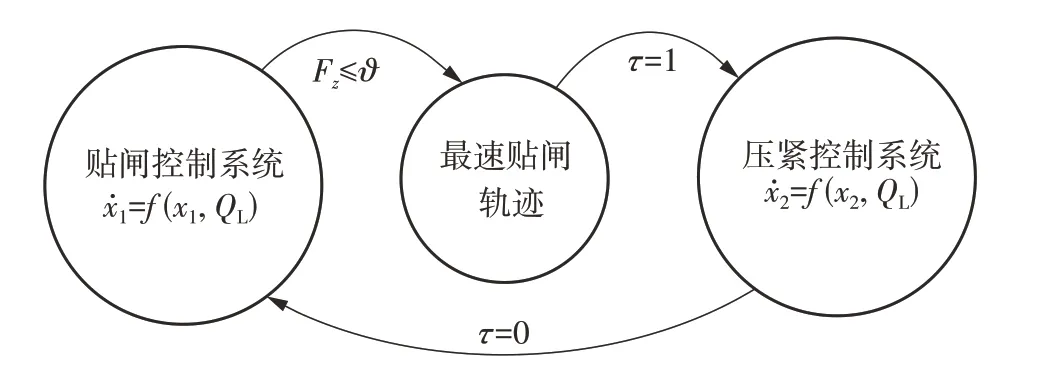
图3 混合贴闸/压紧控制切换原理图Fig.3 Schematic diagram of switching of hybrid shoe-approaching and braking control

式中，QpL为贴闸控制模式下的系统输入，QfL为压紧力跟踪控制模式下的系统输入。

2.1 贴闸控制器

在本节，提出了一种双闭环控制结构以便在存在扰动以及流量和压力约束的情况下，实现电液制动系统最短时间贴闸和高精度跟踪控制。控制器的具体结构如图4所示。外环：为了实现最短时间的贴闸过程，在流量和压力约束下，基于二阶离散积分器设计一种在线最小时间贴闸轨迹规划算法。以这种方式，当闸瓦的初始位置与终点位置误差较大时，在满足约束条件的情况下使再规划后的贴闸轨迹xr(t)能够以最快速度收敛至期望轨迹xd(t)，保证了系统的快速瞬态响应；内环：为解决制动器的贴闸轨迹跟踪问题，通过利用快速终端滑模控制来解决，进而实现有限时间响应和高稳态跟踪精度。

图4 最小时间贴闸控制方案Fig.4 Minimum-time shoe-approaching control scheme

2.1.1 最速贴闸轨迹在线规划

阀控制动器的贴闸控制约束包括伺服阀的流量和油源压力约束，这两种约束可以转化为制动器的速度和加速度约束，可以表示如下

式中，分别为制动器的速度下界和上界；ẍ-、分别为制动器的加速度下界和上界。贴闸轨迹规划的约束设定取决于制动系统的性能参数。具体来说，考虑伺服阀的最大流量、制动器尺寸、内泄漏以及其他影响因素设计给出速度约束̇和̇；考虑到制动器活塞运动阻尼、负载惯性以及其他非线性摩擦综合给出加速度约束和根据制动器流量连续性方程，设计制动器速度边界为

式中：为满足流量限制下制动器速度下界和上界；是制动器预设流量限制。根据制动器的负载力平衡方程，设计制动器加速度边界为

式中，为满足压力限制下的制动器加速度下界和上界；p+L、p-L为盘式制动器预设压力限制。制动器的综合速度约束为

式中，为制动器的预设常数速度约束。制动器的综合加速度约束由下式给出：

式中，为制动器的预设常数加速度约束。本文利用一种基于双积分器的非线性滤波器实现贴闸轨迹在线规划。再规划贴闸轨迹可以在满足速度约束式（12）和加速度约束式（13）的条件下，在最短时间内达到期望的参考信号。重新规划贴闸轨迹xr的过程以在线优化问题的形式表示如下：

式中，T为控制系统的采样周期，*(ktT)为*在kt个采样周期时的值。xr(ktT)和的计算公式如下：

当kt=0时，初始状态量满足式（14）要求。本文利用文献［18］中的非线性滤波器解决式（14）中的在线最优化问题，实现贴闸轨迹的再规划。

2.1.2 非线性贴闸控制器

定义状态跟踪误差向量ep=[ep1，ep2，ep3]T为

式中，αp1、αp2分别为状态变量xp2和xp3的虚拟控制量。设计虚拟控制律αp1为

式中，kp1＞0为反馈增益。对跟踪误差ep2求其关于时间的导数，结合式（6）和式（16）得到：

由式（18）可以得到虚拟控制律αp2为

式中，kp2＞0为反馈增益，其大小对状态误差ep2的收敛速度有直接影响。利用式（6）和式（16）中的第3项，计算跟踪误差ep3关于时间的导数：

为提高系统的收敛速度与鲁棒稳定性，利用快速终端滑模技术，设计全局快速终端滑模面s如下：

由于式（22）中包含负的分数幂(p1-q1)/q1＜0，因此当es=0时存在奇异性问题。为解决式（22）中可能存在的奇异性问题，选用文献［19］中的φ(*)函数对奇异项进行替换，式（22）可以改写为

式中，α2＞β2＞0表示控制反馈调节增益，1＜p＜q表示奇数。

2.2 压紧控制器

本节利用反步理论进行压紧控制器设计，定义压紧控制系统状态跟踪误差为

式中，Fd为制动器的参考制动力信号，ef1为制动力跟踪误差，ef2为系统速度跟踪误差，αf1为滤波后一阶虚拟控制律，αf2为滤波后的二阶虚拟控制律。受限于篇幅限制，本节简化压紧控制器的推导过程，直接给出最终控制律为

中间控制律为

式中，＞0，i=1，2，3为控制反馈调节增益。

2.3 自主切换策略

一般情况下，混合切换系统需要找到一个在任意切换点均是稳定的Lyapunov函数，但是找寻这样一个函数是比较困难的，因此本文通过以制动力为反馈信号，选取合适的力阈值点ϑ来制定切换规则，从而保证制动系统由贴闸控制切换压紧控制时避免出现任何振荡、极限环以及滑动等问题。然而，由于瞬态冲击和瞬态振荡可能会发生在某个边界范围内，因此在Fz=ϑ时直接进行切换似乎是不太合理的。除了瞬态效应外，传感器噪声也会极大影响自主切换的性能。为了避免上述问题，相关研究人员提出了一种具有滞后性的非理性继电器，即进行延迟切换，这使得在Fz=ϑ点形成制动力容限层。这种基于滞回原理的切换逻辑可以描述为

系统的初始状态为

式中，Fϑ=Fz-ϑ表示切换逻辑函数的输入；ϑr为力切换点边界。当τ=0时制动系统处于贴闸控制模式，τ=1时制动系统处于压紧控制模式。值得注意的是，基于滞回原理的切换策略包含有不连续点，并在设定阈值点ϑ进行切换，因此贴闸与压紧控制器之间的变换没有瞬时延时的现象发生。

3 稳定性分析

定理1针对制动系统式（6），选用全局快速终端滑模面式（21），设计控制律式（25）作为贴闸控制模式下的控制输入，则贴闸控制系统是全局渐进稳定的。

证明选取Lyapunov函数V1为

对式（32）求其关于时间的一阶导数，得到：

定义向量χ1=[ep1，ep2，s]T，矩阵Λ1=diag(kp1，，α2)，式（33）可以改写为

式中，l1=2 min{kp1，kp2，α2}。对式（34）两端积分得到：

根据式（35）可知，当t→∞时，V1→0，进而可以得出，贴闸系统式（6）在选择控制输入式（25）的情况下能够保证跟踪误差ep1、ep2，以及全局快速终端滑模面s渐进稳定，即贴闸系统是全局渐进稳定的。

定理2针对制动系统式（6），选用控制律式（27）作为压紧控制模式下的控制输入，则压紧控制系统是全局渐进稳定的。

证明定义Lypunov函数V2为

求式（36）关于时间的导数，得到：

对式（37）两端积分得到：

式中，l2=2 min{kf1，kf2，kf3}。根据式（38）可知，当t→∞时，V2→0。通过以上稳定性分析可知，针对压紧系统式（6），采用控制输入式（27）的情况下能够保证跟踪误差，以及渐进稳定，即压紧系统是全局渐进稳定的。

4 实验研究

为验证本文所提出控制器的性能，在所搭建的如图5所示的单绳缠绕式提升系统进行试验。

实验台的控制系统是基于Matlab/Simulink快速原型技术开发，该平台可以提供高性能的主机目标原型开发环境，然后由主机上的Microsoft Visual Studio.net进行编译，最后下载到目标计算机进行实时执行，系统的采用频率为1 kHz。提升系统具体规格参数取值如下：制动器粘性阻尼系数B=7 500 N·s/m，油液弹性模量βe=1×109Pa，制动器内泄漏系数Ct=4.9×10-15m3/(s·Pa)，制动器刚度系数kf=1.3×107N/m，制动器有效作用面积Ap=0.35×10-3m2，制动器总容积Vt=1.41×10-5m3，供油压力Ps=7×106Pa，回油压力Pr=0，活塞及负载质量m=0.95 kg。

对于本文所提出的矿井提升机制动瞬态冲击抑制策略的控制参数主要包括3部分：（1）贴闸控制器参数kp1＞0、kp2＞0、α1＞β1＞0、α2＞β2＞0、q1＞p1＞1、q＞p＞1和γmin；（2）压紧控制器参数kf1＞0、kf2＞0、kf3＞0；（3）自主切换策略参数ϑ和ϑr，这些参数的选择过程如下所示。

步骤1根据仿真模型设定参数kp1、kp2、α1、β1、α2、β2、q1、p1、q、p和γmin的初值，其中kp1和kp2分别为状态跟踪误差ep1和ep2的系数，其主要作用是调节线性收敛速度，增大kp1和kp2可以缩短收敛时间，但参数过大会引起系统的抖振，推荐取值为kp1∈[300，1 200]、kp2∈[200，800]，且kp1＞kp2。α1、β1、q1、p1决定es的收敛时间，其中α1为滑模面s中一次项es的系数，表示在远离平衡状态时起到主要的线性收敛作用；指数项|es|p1/q1sign(es)系数β1可以在接近平衡状态时起到主要的指数收敛作用。因此，α1和β1共同决定了es收敛到平衡状态的时间，通过增大α1和β1可以减小收敛时间，但是数值过大又会引起抖振现象，因此取α1=150、β1=0.1；q1、p1为指数项|es|p1/q1sign(es)的参数，其值对收敛时间的影响较为复杂，这里一般设定限制条件是q1、p1为正奇数，且p1＜q1。α2、β2、q、p决定滑模面s的收敛时间，可以参考前文中α1、β1、q1、p1的设计原则进行取值；γmin为函数φ(*)的设计参数，其主要作用是解决奇异性问题，在|es|＜γmin时，滑模面s切换至具有非奇异性质的滑模面，因此γmin的取值尽可能小。

步骤2根据仿真模型设定压紧控制器参数kf1、的初值。kf1、kf2、kf3分别为状态跟踪误差ef1、的系数，增大kf1、kf2、kf3可以提高制动力跟踪精度并减小收敛时间，但是过大的取值又会引起系统的抖振问题。因此，推荐取值为∈[400，1 200]、

步骤3调节自主切换策略参数ϑ和ϑr，ϑ决定了切换点大小，其取值一般与制动力的目标值Fd相关，推荐取值为ϑ=(0.3～0.5)Fd；ϑr主要作用是在切换点ϑ形成容错层，防止由于传感器噪声而引起的切换抖振问题，其取值取决于传感器的精度、采样精度和测量噪声。

步骤4在实验过程中，需要关注系统的响应时间、误差大小、控制稳定性等指标，对控制参数进行微调，直至达到令人满意的控制效果为止。

为验证本文所提出控制器在减小贴闸时间和制动瞬态冲击抑制方面的优势，选择以下对比方法。

（1）C1控制器 制动全过程采用本文2.2节所设计的压紧控制进行制动控制。

（2）C2控制器 制动过程分为贴闸与压紧控制，分别采用本文2.1节与2.2节所设计的控制器，贴闸轨迹参考曲线为xd。此外，两种控制模式的切换过程为直接切换，以制动力Fz＞0为切换点。

（3）C3控制器 本文所提出的混合贴闸/压紧控制策。贴闸控制器参数为kp1=850、kp2=530、c1=100、p1=3、q1=5、p=3、q=5、α1=150、α2=150、β1=β2=1×10-3、γmin=1×10-4；再规划轨迹初始设定速度边界=[-0.2，0.2]m/s、初始设定加速度边界=[-12，12]m/s、压力限制[P-L，P+L]=[-5，5]MPa、伺服阀流量限制[Q-L，Q+L]=[-10，10]L/min；压紧控制器参数为=770、=450、=220；制动力切换点ϑ=1 000 N；制动力切换边界点ϑr=500 N。

提升系统的制动控制策略选用恒减速制动，以卷筒转角为反馈信号，采用PID控制器来获取制动力参考信号。提升系统以1 m/s匀速下降，在提升高度为3 m处开始进行紧急制动，设定参考减速度为-0.5 m/s2，闸瓦初始位置xp0=-5 mm。实验主要从制动器贴闸时间、最大制动力误差以及提升钢丝绳张力3个方面对C1、C2和C3的制动性能进行对比。

制动器闸瓦位置与制动力跟踪曲线分别如图6和图7所示。可以看出，与C1相比，C3不仅使得贴闸时间大大缩短，而且制动力冲击得到了较好的抑制。由于C1的贴闸时间取决于当前期望制动力、反馈增益和闸瓦间隙，增大反馈增益可以减小贴闸时间，但这样会使得制动力出现振荡，导致系统不稳定，在图7（a）中体现的尤为明显。C3将贴闸段设计为位置控制，对贴闸轨迹进行在线规划，并利用快速终端滑膜控制实现闸瓦位置快速跟踪，从而取得了较短的贴闸时间。尽管C2取得了最短的贴闸时间，但从图7（b）和7（d）可以看出，C2的瞬态制动力误差同样是3个控制器中最大的。由于C2以阶跃信号xd为参考信号，闸瓦在与闸盘贴合瞬间仍具有较大的速度，在很短的时间内使得制动力产生了较大的超调量，进而引起了制动冲击现象。相较于C2，C3以图6中再规划曲线xr为参考信号，闸瓦在与闸盘贴合前开始减速，从而避免C2中存在的贴合前未减速的问题。从图8可以看出，xr在加速度段和匀速段均满足系统约束，这保证了贴闸时间上要求。此外，由于引入了滞后切换策略，使得制动系统较为稳定地切换至制动力闭环，避免了C2在Fz=0切换点上的抖振问题。

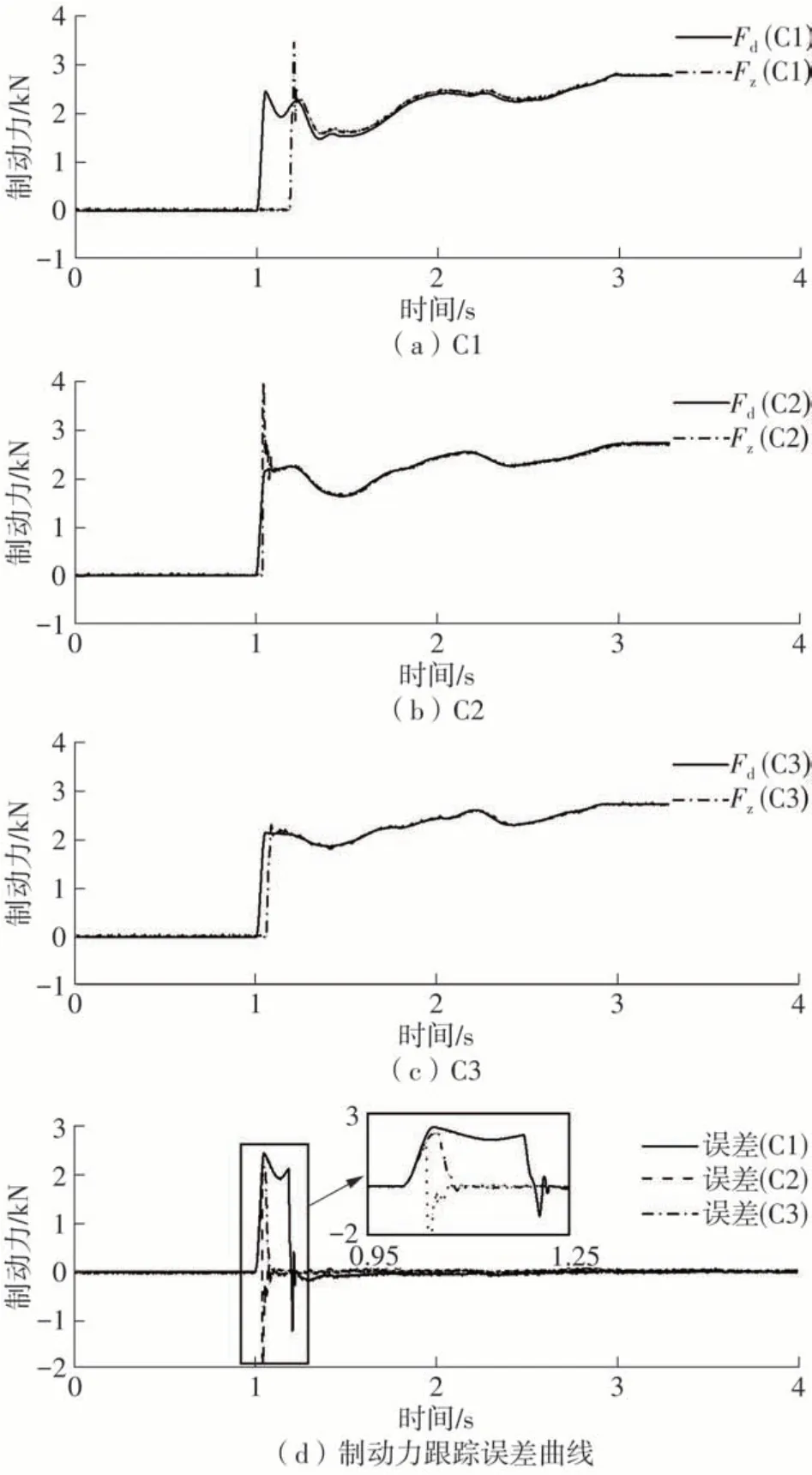
图7 3种不同控制器制动力跟踪曲线Fig.7 Braking pressure tracking curves with three different controllers

图8 再规划贴闸轨迹速度与加速度曲线Fig.8 Planned velocity and acceleration curves of the shoeapproaching trajectory

为了进一步说明本文所提出制动控制策略对提升系统的影响，对制动过程中提升钢丝绳的张力进行了监测。从图9可以看出，采用本文所提出的制动控制策略，可减小制动过程中钢丝的张力值。为更清楚表现本文所提出控制器的优越性，将3种控制器的性能参数统计于表1。

表1 3种不同控制器的性能指标Table 1 Performance indicators with three different controllers

5 结论

针对单绳缠绕式矿井提升机电液制动系统，提出了一种制动瞬态冲击抑制控制策略，在该策略中集成了具有滞后自主切换策略的混合贴闸/压紧控制。当系统接收到制动命令后，利用贴闸控制器实现制动器的贴闸动作，在完成贴闸动作后，利用滞回切换原理使制动系统由贴闸控制稳态切换至压紧控制。此外，在贴闸控制器设计中使用了一种基于二阶离散积分器的在线贴闸轨迹再规划方法，使得制动系统在流量和压力约束下以最短时间完成贴闸动作。最后，通过对比实验结果证明了本文所提出的混合贴闸/压紧控制策略能有效抑制制动瞬态冲击问题，减小制动空动时间，提高制动的安全性。