铁路货车闸瓦上下偏磨机理研究
2018-03-21孙可心卢碧红朱建宁曲宝章
孙可心,卢碧红,朱建宁,曲宝章
(大连交通大学 机械工程学院,辽宁 大连 116028)
0 引言
铁路货车基础制动装置是传递和放大制动动力并产生制动力的部分[1].闸瓦是制动力传递终端,闸瓦性能直接影响列车制动性能. 铁路货车运用中,闸瓦故障主要有闸瓦丢失、闸瓦偏磨、闸瓦裂损、金属镶嵌等[2]. 闸瓦偏磨包括闸瓦上下偏磨、闸瓦左右偏磨、闸瓦斜偏磨. 闸瓦属于磨耗件,闸瓦偏磨不但增加检修负担,而且会导致闸瓦不能与轮箍踏面正常接触而危及行车安全. 闸瓦上下偏磨是发生在列车运行中动态、复杂的接触力学与摩擦学问题,基于目前技术水平难以在列车实际运行中观测闸瓦偏磨过程. 因此,目前在闸瓦上下偏磨形成过程的研究方面,相关研究人员大多采用经验法在闸瓦前端机构中探究影响闸瓦空间姿态的因素,进而定性地讨论各因素对闸瓦上下偏磨的影响[3- 5]. 此类研究方法仅探究导致闸瓦上下偏磨的间接原因,未从理论角度对闸瓦上下偏磨的直接原因进行精确、定量分析.
本文运用解析法推导出闸瓦上下端压力比与闸瓦上下端磨耗量的关系,从动力学、摩擦学角度分析闸瓦上下偏磨形成过程,并结合新一代多体动力学软件RecurDyn对转向架基础制动装置进行多体动力学仿真验证,采用解析法与仿真实验结合的方法来研究闸瓦上下偏磨形成过程.
1 闸瓦制动瞬时受力模型
1.1 闸瓦制动三阶段
闸瓦上下偏磨程度可以用闸瓦上下端磨耗量差值的绝对值大小来衡量,绝对值越大表明闸瓦上下偏磨程度越大. 闸瓦磨耗速率定义为单位时间内闸瓦磨耗量. 当闸瓦上下端初始厚度相等时,闸瓦上下端磨耗量不等的直接原因为闸瓦上下端磨耗速率不等,而闸瓦上下端磨耗速率又与闸瓦上下端压力比密切相关. 因此,研究闸瓦上下偏磨问题首先必须抽象出闸瓦制动单元瞬时受力模型,之后再运用解析法求解出闸瓦上下端压力比,进而探究压力、磨耗速率、磨耗量之间的动态关系.
已经存在一定上下磨耗量的闸瓦其制动过程可分为三个阶段:闸瓦靠近车轮阶段、闸瓦调整姿态阶段(发生角度偏转阶段)、闸瓦抱紧车轮阶段,如图1所示.
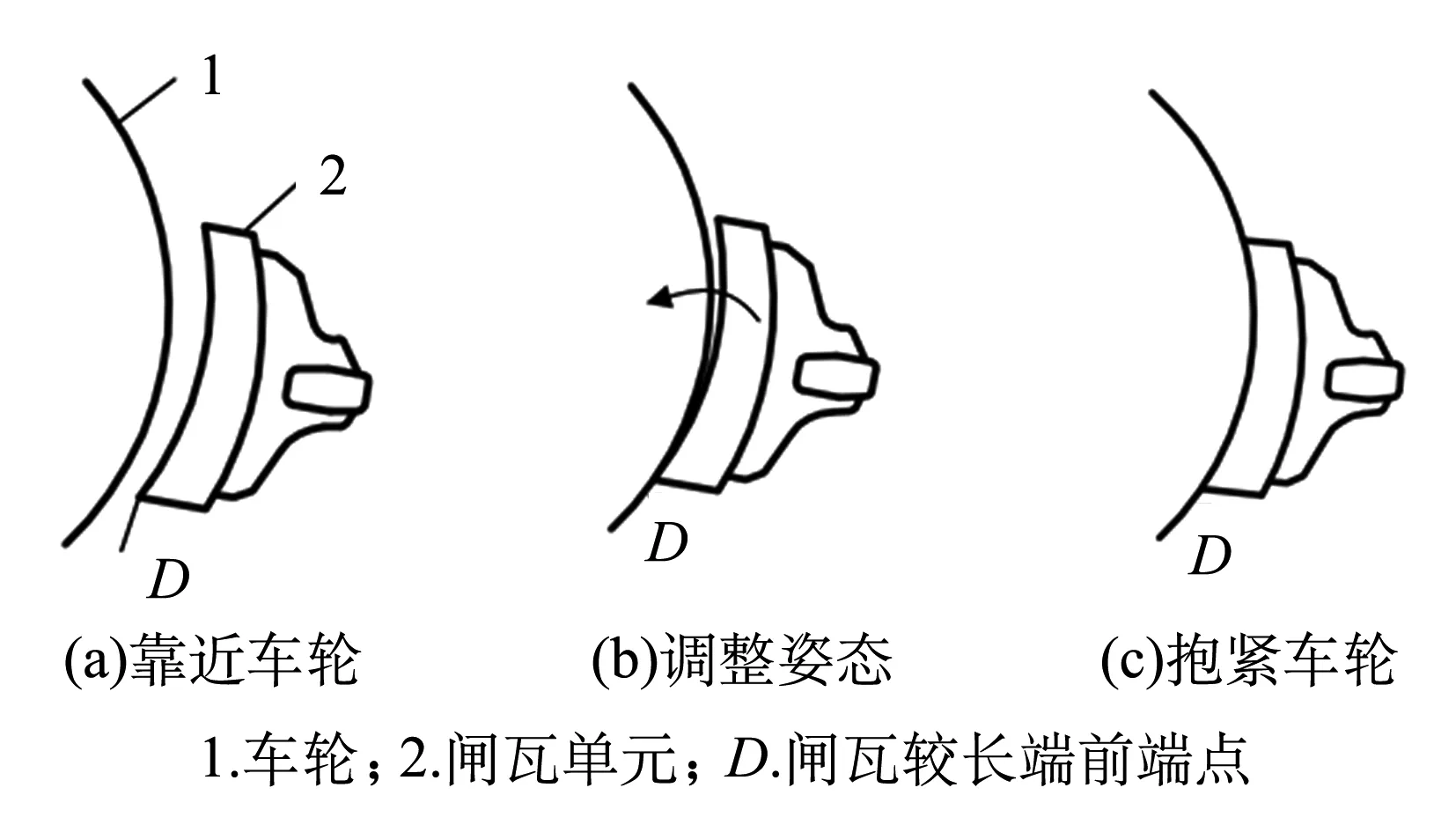
图1 闸瓦制动过程示意图
闸瓦靠近车轮阶段:闸瓦沿着滑槽平动,直至闸瓦较长端前端点D与车轮接触;闸瓦调整姿态阶段:闸瓦以较长端前端点D为中心旋转(旋转角度受滑槽的制约),直至闸瓦弧面与车轮完全接触;闸瓦抱紧车轮阶段:闸瓦与车轮紧密贴合,不再发生相对位移,且制动力逐渐增大到某一值后保持不变.
1.2 制动单元瞬时受力模型
闸瓦磨耗主要发生在闸瓦抱紧车轮阶段,故对此阶段闸瓦制动单元进行合理简化与力学分析. 分析前作以下假设:
(1)闸瓦与车轮均视为刚体,不发生形变,且在制动稳态阶段二者弧面完全接触;
(2)滑槽与滑块间作用力视为单一点接触;
(3)车轮对闸瓦的分布压力等效为作用于闸瓦上、下两端的集中力;
(4)受力分析时,不计滑槽对滑块的摩擦阻力及制动单元自身重力;
(5)当闸瓦上端磨耗量大于下磨耗量时,闸瓦下端点先与车轮接触,且假设此时下端接触点与未偏磨时下端接触点相同;当闸瓦上端磨耗量小于下磨耗量时,闸瓦上端点先与车轮接触,且假设此时上端接触点与未偏磨时上端接触点相同.
在闸瓦运用过程中某一瞬时闸瓦上下端已存在一定磨耗量,且不同位置的闸瓦,车轮的旋入端也不同.故假设任意时刻某位闸瓦上下端磨耗量分别为δ1、δ2,以研究车轮不同旋向时,闸瓦上下端压力分布情况. 对于列车任一转向架,闸瓦制动单元存在四种不同受力模型:δ1>δ2,上端为旋入端;δ1>δ2,下端为旋入端;δ1<δ2,上端为旋入端;δ1<δ2,下端为旋入端.现针对δ1>δ2且上端为旋入端情况进行研究,其受力模型如图2所示.
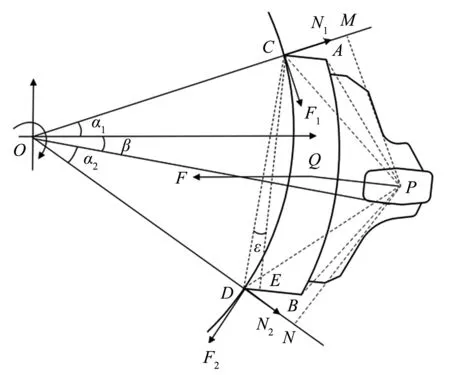
图2 闸瓦制动单元瞬时受力模型
图中P为滑块质心;O为车轮旋转中心;A、B为闸瓦上、下端后端点;C、D为闸瓦上、下端前端点;α1为OC连线与水平面夹角;α2为OD连线与滑槽夹角;ε为闸瓦旋转角;β为滑槽倾角;N1、N2为车轮对闸瓦上、下端的正压力,作用点分别为C、D;F1、F2为车轮对闸瓦上、下端的摩擦力,作用点分别为C、D;N为滑槽对滑块的支反力,作用点为P;F为制动梁所受制动力,作用点为Q;PM为N1对P点取矩的力臂长;PN为N2对P点取矩的力臂长;CE为闸瓦上下端垂直距离.
对于此型转向架:车轮半径OC=OD=420 mm;闸瓦上端厚度AC=(46.63-δ1)mm;闸瓦下端厚度BD=(46.63-δ2)mm;滑块质心到闸瓦上、下端后端点距离PA=PB=216.36 mm;PQ=137.85 mm;∠PAC=∠PBD=126°;闸瓦上下端距离CE=352 mm;滑槽倾角β=12°;OC连线与水平面的夹角α1在本工况下为一变量,其值为闸瓦上下磨耗量δ1、δ2的函数;OD连线与滑槽夹α2=25°;闸瓦旋转角ε为一变量,其值为闸瓦上下磨耗量δ1、δ2的函数;制动梁所受制动F=23 755 N.
1.3 闸瓦瞬时受力分析
根据图2所示闸瓦单元瞬时受力模型,列平面一般力系平衡方程:
(1)
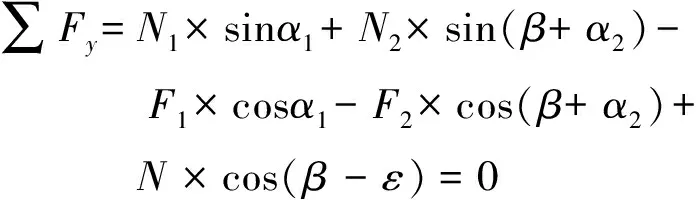
(2)
约束条件:ε<12°,0≤δ2<δ1≤30,且δ1、δ2∈Z.
其中,L1、L2、L3、L4、L5为力N1、N2、F1、F2、F的力臂长度,其值均为闸瓦上下磨耗量δ1、δ2的函数. 其函数关系如下:
函数中PC、PD、∠ACP、∠BDP、α1、ε又均为闸瓦上下磨耗量δ1、δ2的函数,其函数关系由余弦定理即可求得.
1.4 闸瓦瞬时受力方程求解结果及分析
联立上述方程(1)~(10),可解得N1/N2与δ1、δ2关系,由于是隐函数不便表达,这里采用数值法,利用MATLAB画N1/N2=f(δ1,δ2)关系曲线如图3所示.
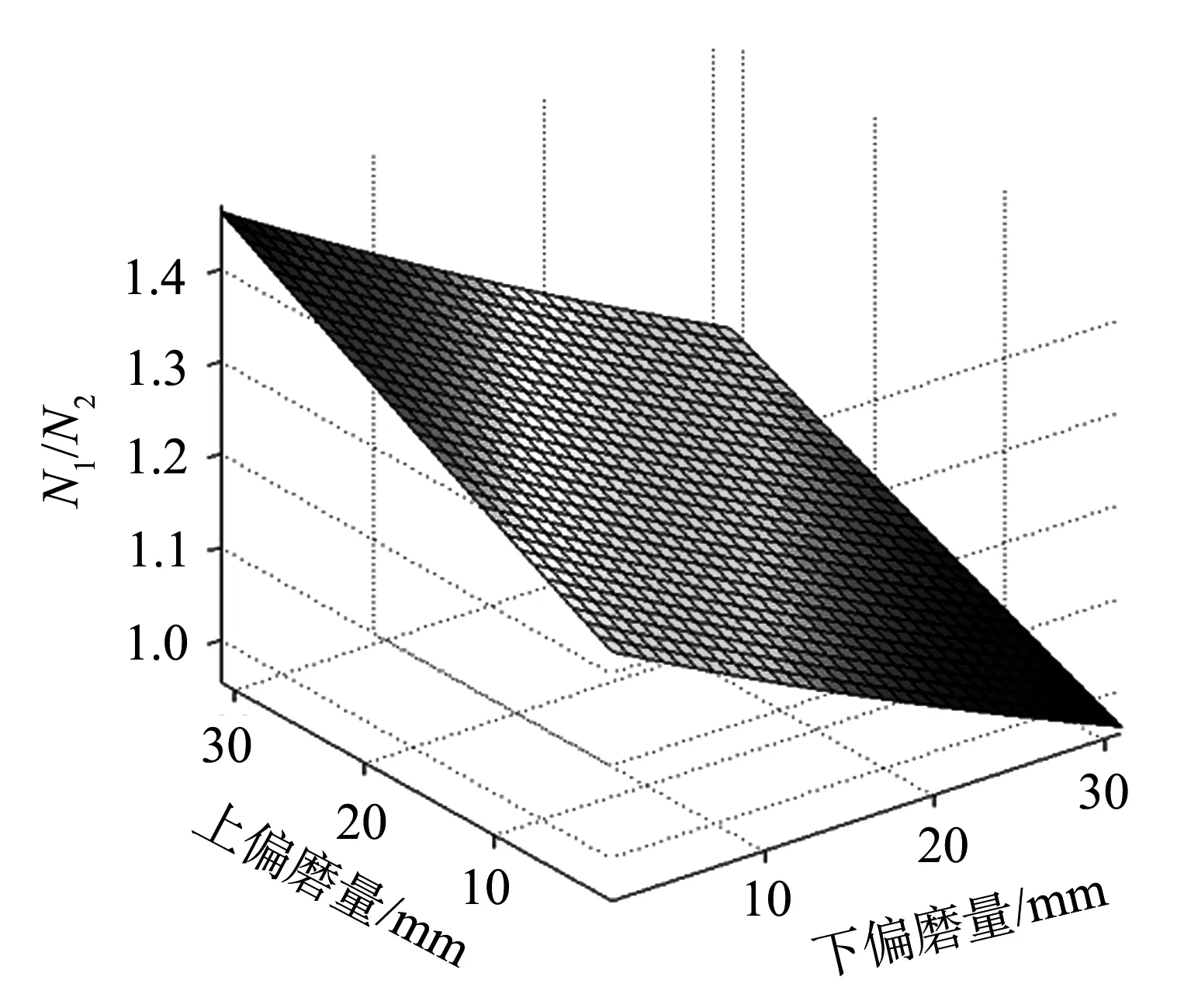
图3 δ1>δ2(上端旋入)时,N1/N2=f(δ1,δ2)图像
由图3可知,对于δ1>δ2且上端为旋入端情况,闸瓦上下端瞬时压力比受闸瓦上下端磨耗量影响. 当上端磨耗量不变时,闸瓦上下端压力比随下端磨耗量增大而减小;当下端磨耗量不变时,闸瓦上下端压力比随上端磨耗量增大而增大.
对于其他三种受力模型,分析方法与δ1>δ2且上端为旋入端类似. MATLAB数值计算结果如下:当δ1>δ2且下端为旋入端时,N1/N2取值范围为0.82~1.04;当δ1<δ2且上端为旋入端时,N1/N2取值范围为1.15~1.21;当δ1<δ2且下端为旋入端时,N1/N2取值范围为0.82~0.87.
2 闸瓦上下偏磨形成过程分析
2.1 转向架去程与回程
闸瓦上下端压力比与闸瓦上下端磨耗量关系为瞬时关系. 而闸瓦上下偏磨为动态的过程,故结合瞬时关系探究闸瓦上下偏磨的形成过程.
任意一节列车工作状态分为去程、回程两种工况. 以二位端转向架为例,将车辆向固定杠杆方向行驶定义为去程;将车辆向游动杠杆方向行驶定义为回程. 对于同一闸瓦而言,去程、回程时车轮旋入端不同,如表1所示.

表1 二位端转向架去程回程各位闸瓦旋入端情况
2.2 去程时闸瓦偏磨形成过程
当车辆去程时,7、8位闸瓦上端为旋入端,此时N1/N2取值范围为1.15~1.46. 初始时闸瓦上下端磨耗量δ1=δ2=0,由图3知此时N1/N2=1.22,即N1>N2. 由于闸瓦磨耗速率与闸瓦压力呈正相关关系,则此时闸瓦上端磨耗速率大于闸瓦下端磨耗速率. 在偏磨初期,将呈现δ1>δ2的情况.
结合图3数据可知,当δ1>δ2时,N1/N2的值将比上下端磨耗量相等时更大,即上端磨耗速率将更大,这将导致偏磨中期︱δ1-δ2︱值逐渐增大.故若行驶方向不变,7、8位闸瓦上偏磨将越来越严重.
2.3 回程时闸瓦偏磨形成过程
当车辆回程时,7、8位闸瓦下端为旋入端,此时N1/N2取值范围为0.82~1.04. 当上偏磨量为24~25 mm时,呈现N1=N2情况. 在去程终态已呈现上偏磨现象,但上下磨耗量具体数值由实际中去程里程数及其他因素综合决定,故需分情况讨论:
(1)去程终态上端磨耗量未达24~25 mm
此时,由MATLAB数值计算结果可知回程时N1/N2<1,闸瓦下端磨耗速率大于上端磨耗速率,︱δ1-δ2︱值减小,上下磨耗量趋于相等,磨耗趋于均匀.
(2)去程终态上端磨耗量已达24~25 mm
由MATLAB数值计算结果可知回程时N1/N2≈1 ,即上端磨耗速率约等于下端磨耗速率,︱δ1-δ2︱值保持不变,即偏磨量保持不变,磨耗未趋于均匀.
2.4 延长闸瓦使用寿命的措施
对于闸瓦检修及维护而言,当闸瓦一端厚度余量小于14 mm时,则需更换闸瓦. 因此,应使闸瓦两端磨耗尽量均匀. 对比2.3中的情况(1)、(2),应尽量使情况(1)发生. 则去程上端磨耗接近24 mm时,列车需反向行驶. 由于列车行进方向不能随意改变,故此方案不可行. 故考虑另一种方案:当上偏磨达一定程度时,将闸瓦上下端对调.
对调后应结合δ1<δ2且上端为旋入端工况数据分析. 此时N1/N2取值范围为1.15~1.21. 即N1始终大于N2,上端磨耗速率始终大于下端磨耗速率,一段时间后,上下端磨耗量差值减小,上下磨耗趋于相等,磨耗趋于均匀. 故建议当车辆检修后发现7、8位闸瓦一端磨耗量达到(46.63-14)/2≈16 mm时,将闸瓦上下对调,以延长闸瓦使用寿命.
由于5、6位闸瓦与7、8位闸瓦在空间上具有对称性,故其上下偏磨形成过程与7、8位闸瓦偏磨过程规律一致. 同样地,为延长闸瓦使用寿命,当车辆检修后发现5、6位闸瓦一端磨耗量达到16 mm时,即可将闸瓦上下对调.
3 闸瓦偏磨仿真实验验证
3.1 实验方案设计
本文通过研究闸瓦上下端压力比与上下端磨耗量关系研究闸瓦上下偏磨形成过程. 仿真实验时通过改变闸瓦三维模型几何外形模拟现实中闸瓦上下端磨耗量,通过提取闸瓦上下端的压力评价该磨耗量时闸瓦上下端磨耗速率. 转向架单程运行时,同时存在两种工况. 对于δ1>δ2且上端为旋入端工况,取δ1值分别为8、12、16,δ2值分别为0、4、8进行闸瓦制动虚拟仿真实验,仿真实验合计9组.
3.2 转向架基础制动装置建模
作为一个多刚体系统,货车基础制动装置各刚体零部件运动通过约束和接触碰撞实现[6]. RecurDyn作为一款采用完全递归算法和相对坐标系运动方程理论的新一代多体系统动力学仿真软件,求解大规模多体系统动力学问题非常便捷精确[7]. 对于模型处理,首先,将Creo环境下的基础制动装置原始三维模型以STEP格式文件导入RecurDyn中,在不影响机构正常运动前提下,对基础制动装置模型进行合理简化与合并. 然后,为实现基础制动装置各零件之间运动关联性,需要在各零件之间添加约束关系. 最后,添加载荷,制动力施加于制动杠杆中间销孔处,取恒值F=47 354 N.
3.3 实验结果分析
仿真实验结果如表2所示.
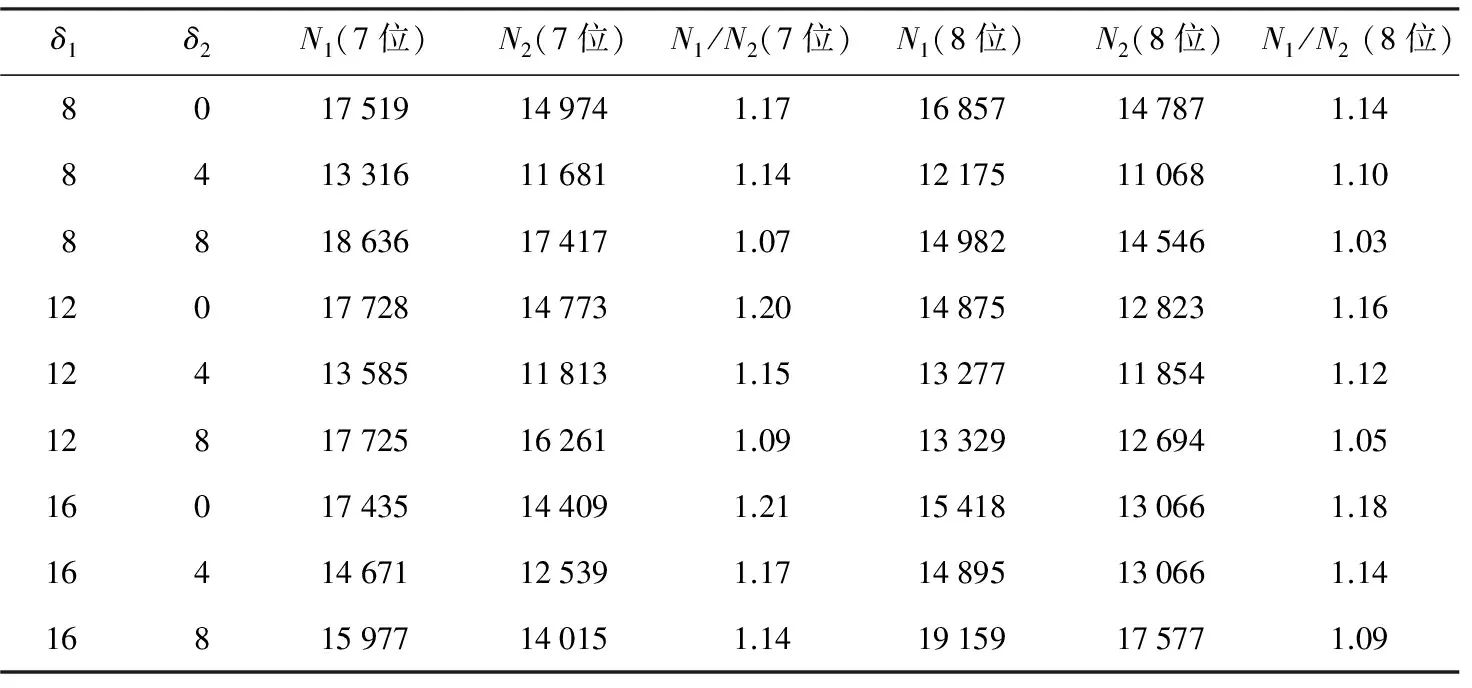
表2 转向架7、8位闸瓦上下端压力 N
仿真结果分析:
(1)同一制动梁上的两闸瓦压力分布情况基本相同,当δ1>δ2且闸瓦上端为旋入端时,同一闸瓦上端点压力均大于下端点压力,与解析法中在该工况下一直呈现上偏磨现象一致;
(2)当闸瓦上偏磨量δ1不变时,N1/N2值随下偏磨量δ2增大而减小,与解析法所得图像变化趋势一致;当闸瓦下偏磨量δ2不变时,N1/N2值随下偏磨量δ1增大而增大,与解析法中闸瓦上偏磨严重程度越来越大一致.
4 结论
(1)通过对制动单元受力分析可知,制动力作用方式及闸瓦初始姿态导致闸瓦的初期偏磨;
(2)磨耗初期闸瓦上下端磨耗量不等导致闸瓦上下端磨耗速率不等,进而导致磨耗中期上下端磨耗量差值增大,最终呈现闸瓦一端偏磨严重现象;
(3)闸瓦上下偏磨程度受去程回程里程数之比影响,具体磨耗情况需结合现场实际运用情况讨论;
(4)当车辆检修后发现闸瓦一端磨耗量为16 mm时,建议将闸瓦上下对调,以延长闸瓦使用寿命;
(5)货车基础制动装置仿真实验数据与解析法求解结果一致.
[1]饶忠, 彭俊彬. 列车制动[M]. 北京:中国铁道出版社, 2010:16- 19.
[2]周磊, 陈雷. 铁路货车主要结构与使用[M]. 北京:中国铁道出版社, 2011:182- 183.
[3]王刚强. GK_(1C)型机车闸瓦偏磨的原因分析及处理[J]. 铁道机车与动车, 2015,492(2):45- 46.
[4]刘小利. DF_4型机车闸瓦偏磨的原因及改善措施[J]. 铁道机车车辆, 2006(5):54- 70.
[5]田艳君. ND_5型机车闸瓦偏磨的原因及解决措施[J]. 内燃机车, 2006(6):43- 48.
[6]LU BIHONG, ZHANG YU, QU BAOZHANG, et al. Research on RecurDyn Based Simulation Method for the Brake Shoe Eccentric Wear in Railway Freight Cars[J]. Key Engineering Materials, 2012, 522:467- 471.
[7]LU BIHONG, CHEN XIAOYUAN, QU BAOZHANG, et al. Research on Wheel-Shoe Wear for High Friction Composite Brake Shoes Based Foundation Brake Rigging in Railway Wagon[J]. Key Engineering Materials, 2015, 667:530- 535.
