基于COA-GRU的低成本气体传感器数据修正方法

李炳伟,叶树霞,齐 亮,张永韡,冯 锦,陈宇霆

江苏科技大学自动化学院

0 引言

低成本气体传感器已经广泛应用于环保、自动化等领域,然而由于其设计和制造的固有限制,存在灵敏度低、准确度不高等缺陷。这些问题严重影响了传感器检测数据的可靠性与精度,特别是需要高精度气体浓度检测的应用场景。检测环境的干扰会造成传感器特性点产生漂移,从而导致测量结果偏离理想值,形成非线性特性。由于传感器设计方案所导致的非线性误差是在出厂前就已经存在的,无法对其进行优化处理[1]。因此,环境干扰是导致传感器测量结果精度下降的主要因素,对环境干扰下的传感器进行数据修正是提高传感器精度的常用方法。

在气体传感器的数据修正方面,文献[2]采用深度学习的方法对非色散红外单通道CO2传感器进行快速标定校准。文献[3]采用多元线性回归和随机森林方法建立校准模型,对CO、NO2、O3传感器进行校准。文献[4]采用多元线性回归分析环境变量的确定系数对低成本CO2传感器进行校准。文献[5]基于监督学习技术开发了低成本CO、NO2、SO2、O3传感器的现场校正系统。文献[6]采用RBF神经网络技术拟合非线性连续函数,解决了传感器在温度、湿度、灰尘的长期影响下导致输出误差过大的问题。文献[7]分析了温度、湿度对低成本传感器的影响,基于线性分析开发了校准模型对低成本PM传感器进行校准。文献[8]采用两步校准方法对低成本传感器进行校准。文献[9]分析了温度、湿度对低成本SO2、CO、NO2传感器的影响并对传感器进行修正。文献[10]对传感器阵列进行了多变量的校准和验证。文献[11]采用PSO-BP神经网络训练传感器数据,实现了实时修正传感器数据的功能。文献[12]提出一种多项式拟合与基于粒子群优化的BP神经网络相结合的非线性校正方法。

针对低成本气体传感器受环境干扰导致检测精度低的问题,本文提出一种COA-GRU神经网络模型用于修正温度、湿度、压力对低成本气体传感器检测精度的影响,提高传感器检测数据的可靠性和精度。

1 基于门控循环单元的传感器数据修正模型

门控循环单元(gated recurrent unit,GRU)是一种简化版的长短期记忆网络(long short-term memory,LSTM),能够解决循环神经网络中存在的梯度消失、梯度爆炸等问题[13],可以用来构建传感器的数据修正模型。GRU神经元包括重置门和更新门两个门结构。GRU神经网络的神经元结构如图1所示:

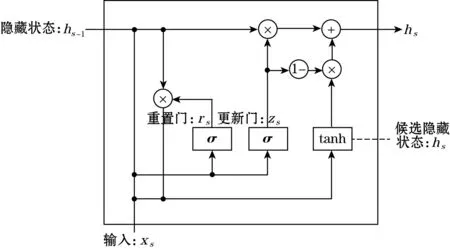
图1 GRU神经网络的神经元结构

1.1 更新门

zs=σ(Wz[hs-1,xs]+bz)

(1)

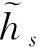
1.2 重置门

rs=σ(Wr[hs-1,xs]+br)

(2)

式中:rs为重置门;Wr和br分别为权重参数和偏执值。

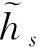
1.3 候选隐藏状态

(3)

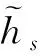
1.4 输出隐藏状态

(4)

式中hs为输出隐藏状态。

把最新的输出隐藏状态进行线性变换,生成输出值。

本文使用门控循环单元神经网络,利用大量数据训练出传感器修正模型后,对传感器数据进行修正。传感器非线性模型如图2所示。

图2 传感器模块非线性模型

传感器模型方程为

y=f(x,υ1,υ2,υ3)+w

(5)

式中:y为传感器输出的检测值;x为实际环境中的待测气体;υ1、υ2、υ3表示环境变量即温度、湿度、压力;w为传感器系统受到的干扰噪声。

假设函数f(x,υ1,υ2,υ3)是一个未知的复杂函数,其与传感器特性以及环境因素有关。根据传感器特性,可以得出在给定环境变量υ1、υ2、υ3的情况下,函数x和y之间存在一种复杂的对应关系。因此,可以推断出一种特殊的函数y=g(f(x,υ1,υ2,υ3)),即寻求一个函数g,使得经过修正的传感器的输出数据可以准确地反映所测气体浓度的大小,其校正原理如图3所示:

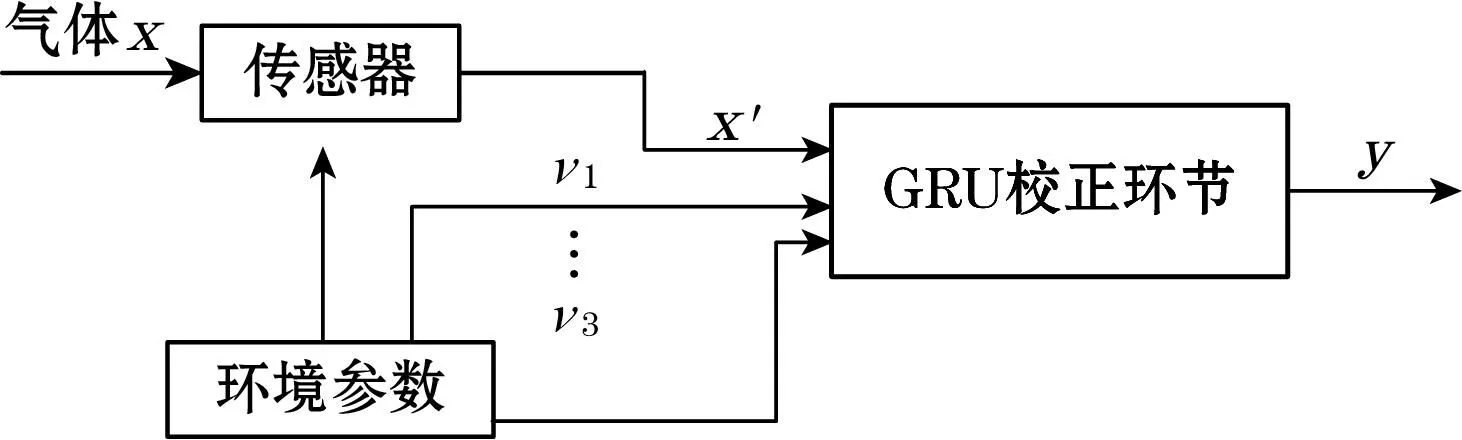
图3 传感器校正原理

GRU神经网络可以被认为一个黑盒,这个黑盒就是函数g,将环境参数(温度、湿度、压力)以及检测的气体浓度作为GRU神经网络的输入,将气体真实浓度作为输出。GRU神经网络通过大量数据训练,建立待测气体与其环境变量之间的非线性黑盒模型,以此来修正传感器检测数据。

2 基于长鼻浣熊算法的修正模型优化

影响GRU神经网络模型训练效果的关键参数主要有学习率(learning rate)、隐藏层神经元(hidden layer neurons)节点数和正则化系数(regularizaiton)等。其中,学习率控制模型更新方向与收敛速度,隐含层神经元个数决定模型的非线性拟合能力,正则化系数主要防止模拟过拟合。选取合适的GRU网络的超参数可以使得模型快速收敛,提高学习的性能和效果。但是GRU神经网络的超参数往往难以确定,不同超参数的选取对训练结果会造成很大的影响,还有可能出现多局部极值的问题。由于长鼻浣熊优化算法(coati optimization algorithm,COA)具有良好的全局寻优能力和收敛速度,于是引入COA对GRU神经网络进行优化,解决GRU神经网络初始参数选择不准确,导致训练模型收敛速度慢和效果不佳的问题。

长鼻浣熊优化算法由M.Dehghani提出,是一种用于全局搜索和局部搜索最优值的改进算法[14]。该算法起源于模拟浣熊群攻击蜥蜴策略和躲避捕食者机制的2种自然行为。COA对浣熊2种自然行为进行建模,浣熊被认为是该算法的群体成员,每个浣熊在搜索空间中的位置决定了决策变量的值,2种自然行为可认为是2个阶段。

第1阶段模拟浣熊群攻击蜥蜴时的策略,在搜索空间中更新种群。在这一策略中,一群浣熊爬上树去围剿一只蜥蜴并吓唬它。其他浣熊在树下等待,直到蜥蜴从树上摔落。蜥蜴摔倒在地后,地上浣熊攻击并追捕它。这种策略使浣熊在搜索空间中移动到不同的位置,这表明了COA在解决空间问题中全局搜索的探索能力。

第2阶段是基于浣熊遇到捕食者和逃离捕食者时的机制更新浣熊在搜索空间中的位置。当捕食者攻击一只浣熊时,它会从自己的位置逃跑。浣熊在此策略中使当前位置接近于安全位置,这表明了COA在局部搜索中的开发能力。COA在全局和局部层面扫描搜索空间的能力较高,并且在识别出主要最优区域后,可以以很高的收敛速度得到最优解。

COA寻找最优解过程如下:

随机初始化浣熊群在搜索空间中的位置:

Xi∶xi,j=lbj+r·(ubj-lbj)

(6)

式中:Xi为第i个浣熊在搜索空间的位置,i=1,2,…,N;xi,j为第j个决策变量的值,j=1,2,…,m;N为浣熊种群的数量;m为决策变量的数量;r为[0,1]的随机实数;ubj和lbj分别为决策变量的上限和下限。

浣熊群矩阵用式(7)表示:

(7)

候选解在决策变量中的位置不同,对问题目标函数值的评估也不同,其值用式(8)表示:

(8)

式中:F为获得目标函数的向量;Fi为第i个浣熊获得的目标函数值。

2.1 狩猎和攻击蜥蜴的策略(探索阶段)

浣熊在树上往上爬的位置用式(9)表示:

(9)

地面上的浣熊在搜索空间中移动搜寻掉落在地上随机位置的蜥蜴可用式(10)、式(11)表示:

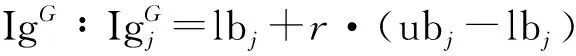
j=1,2,…,m

(11)

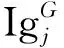
判断是否更新浣熊位置:

(12)

2.2 逃离捕食者的过程(开发阶段)

在每个浣熊所在位置的附近生成随机位置,用式(13)、式(14)表示:

(13)

(14)

式(15)为选择生成位置:

(15)

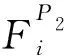
如果新生成位置提高了目标函数的值,则更新浣熊的位置。

根据第1阶段和第2阶段更新搜索空间中所有浣熊的位置后,COA的迭代完成。根据式(9)～式(15)重复更新种群,直到算法的最后一次迭代。COA运行完成后,将所有算法迭代期间获得的最优解作为输出。

本文提出了一种新的组合模型COA-GRU对传感器数据进行修正,将COA的最优解赋值给GRU神经网络的超参数。COA-GRU的优化流程图如图4所示。

图4 COA-GRU优化流程图

3 实验与结果分析

3.1 实验环境与数据来源

3.1.1 实验环境

本文实验均在64位的Windows10操作系统下完成,平台基于C++的MatlabR2022b,计算机CPU为11th Gen Intel® CoreTMi5-11400H,GPU为NVIDIA GeForce RTX 3050,内存为16 GB。

3.1.2 数据来源

本文采用的SO2、CO、NO2、CO2低成本气体传感器组的型号分别为PR-3002-SO2、MQ-7、Figaro-TGS2600、JX-CO2-102,检测精度分别为±5%F·S、±10F·S、±10F·S、±5%F·S。为了建立实际应用中环境参数对传感器影响的模型,获得更加准确的传感器修正数据,本文将传感器组置于镇江港4003拖轮船已安装的H200D气体检测装置的检测室内。传感器组与H200D气体检测仪器共用一个气体预处理装置和检测室,每min记录1次环境参数和气体浓度,并使用H200D气体检测装置测得的数据作为参比数据。H200D气体检测装置检测精度小于±2%F·S,分辨率为0.01 ppm(1 ppm=10-6),测得的气体浓度可认为气体的真实浓度。记录8.5 h,共500组数据,其中80%作为训练集,20%作为测试集。实验装置如图5所示。

(a)低成本传感器组

3.1.2.1 参数设置

本文以检测室的压力、气体温度、湿度、原始气体浓度数据作为COA-GRU网络的输入,H200D设备测得的气体浓度作为输出,对COA-GRU修正模型进行训练。

GRU网络的重置门和更新门选择Sigmoid函数作为激活函数。生成候选隐藏状态时使用tanh函数作为激活函数。全连续层中采用Relu函数作为激活函数。将均方根误差(RMSE)设为损失函数。

设置COA初始的浣熊种群成员数量为50,算法迭代次数为30。COA-GRU网络训练参数设置如表1所示。

表1 COA-GRU网络训练参数设置

3.1.2.2 数据归一化

在COA-GRU对传感器数据进行修正前,首先对测得的数据进行归一化处理,数据归一化处理是为了提高模型的收敛速度,避免不同指标数值区间的差异性,消除不同量纲对修正结果的影响。本文采用mapmaxmin函数对各影响因素下的检测数据进行归一化处理,经处理后的指标数值按固定比例缩放至[0,1]范围内,数据归一化公式为

(16)

式中:y为各影响因素下气体浓度归一化的值;xmin和xmax分别为y对应的最大值和最小值;ymin和ymax分别为xmin和xmax归一化后对应的最大值和最小值;x为各影响因素下的气体浓度值。

本文选择Adam算法更新修正模型中的权重。虽然Adam优化算法可以自适应地调整学习率,但训练修正模型具有一定的随机性,并且在更新权重时使用了动量和自适应学习率等技术,从而造成其搜索空间较为广泛,可能导致出现多个局部极值的问题。

为了判断修正模型是否存在多个局部极值的问题,验证COA优化GRU神经网络的必要性。选择500组环境参数数据以及SO2浓度数据作为训练数据集,其中70%作为训练集,30%作为测试集。随后设置超参数的搜索范围,其中学习率[0.001,0.05]、隐藏层数[10,100]、正则化系数[0.001,0.01]。使用不同的超参数组合训练GRU神经网络,并记录每个超参数组合的均方根误差。最后,将参数组合绘制成三维图表,其中横轴表示隐藏层数,纵轴表示学习率,深度轴表示正则化系数,点的颜色表示均方根误差的大小。超参数三维图如图6所示:

图6 超参数三维图

由图6可知,超参数三维图中颜色最深的点存在多处且比较分散,可以得出GRU神经网络修正模型存在多局部极值的问题。所以本文有必要采用COA优化算法在全局范围内寻找最佳参数组合,从而提高数据修正模型的性能和准确性。

3.2 实验结果分析

COA优化的GRU网络的适应度值随迭代次数变化如图7所示:

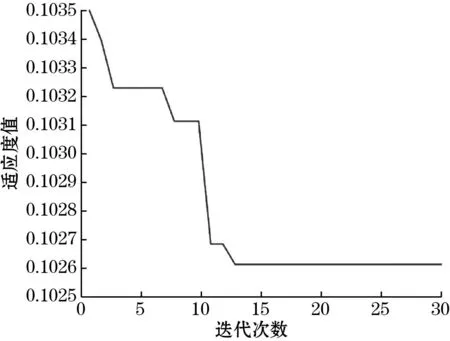
图7 适应度值

由图7得出,COA优化的适应度值随着迭代次数增加而逐渐降低,最后趋于平稳状态,说明COA-GRU模型的训练效果较好,COA优化后的GRU神经网络具有更快的收敛速度、更好的学习效果和性能。

选取PR-3002-SO2与H200D同时间段对SO2检测浓度作为验证数据来测试COA-GRU修正模型效果,同时判断是否存在过拟合问题。部分测试结果如图8所示。

图8 COA-GRU网络修正结果

由图8可以得出,经过修正的测量值更接近H200D的检测值。以H200D的测量值为真实参考值,测试集绝对误差曲线如图9所示。

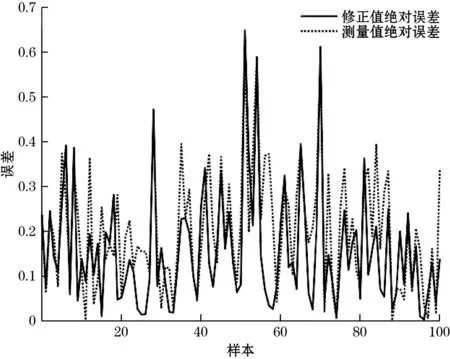
图9 测试集绝对误差曲线图

由图9可以得出,修正后的绝对误差基本小于测量值的绝对误差,可以得出经过COA-GRU模型对传感器数据进行修正可以提高对SO2的检测精度。本文采用决定系数(R2)、均方根误差、平均绝对误差(MAE)与平均绝对百分比误差(MAPE)来量化评估COA-GRU模型的修正性能。不同算法对SO2修正的效果如表2所示。

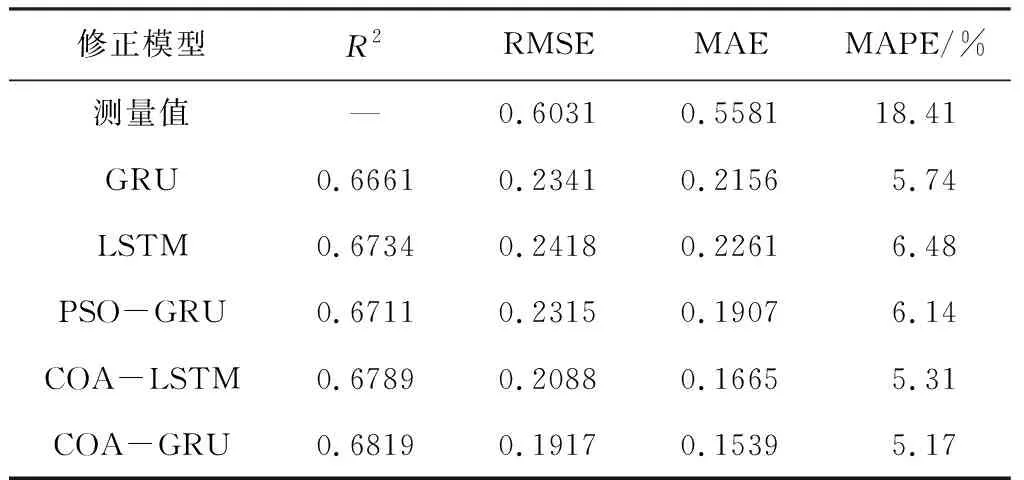
表2 SO2修正精度对比

由表2可知,PR-3002-SO2传感器的原始测量值均方根误差远大于修正值均方根误差,修正后的平均绝对误差相比于测量值减少72%,均方根误差减少了68%,平均绝对百分比误差减少了72%。COA-GRU模型在均方根误差、平均绝对误差、平均百分比误差上小于任何一个修正模型。

为了验证COA-GRU对其他气体的修正效果,分别对CO、NO2、CO2的浓度、烟气参数历史数据进行训练,训练后的各气体传感器数据修正模型测试结果如图10所示。

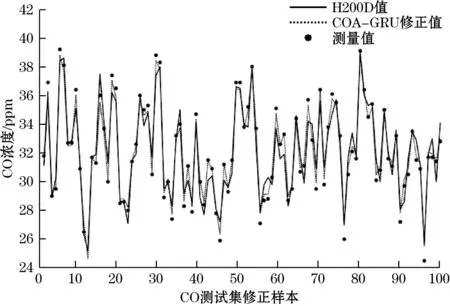
(a)CO修正结果

从图10可以得出,COA-GRU修正模型对各类气体传感器数据的修正值相较于测量值更加接近H200D烟气检测装置的值,修正曲线比传感器测量曲线更接近H200D检测曲线。说明COA-GRU修正模型在对传感器数据修正方面具有较好的效果和较强的普遍适用性。

为了更加直观地分析COA-GRU修正模型在CO、NO2、CO2传感器数据修正效果,依旧采用决定系数、均方根误差、平均绝对误差与平均绝对百分比误差评估修正模型的效果,结果如表3所示。

表3 各类气体传感器数据修正结果对比

由表3可以得出,基于COA优化的GRU神经网络的修正模型对CO、NO2、CO2传感器数据修正的均方根误差均小于测量值的均方根误差,平均绝对误差相比于测量值分别降低了28.4%、29.6%、13.5%,平均绝对百分比误差相比于测量值分别降低了27.9%、46.3%、17.8%。COA-GRU模型的修正值与H200D检测值的误差均小于PSO-GRU修正模型以及原始的GRU和LSTM模型。实验结果表明经过大量数据训练后的COA-GRU网络修正模型对SO2、CO、NO2、CO2传感器检测的数据有良好的修正效果。

4 结束语

本文提出了一种基于COA-GRU的传感器数据修正方法,用于提高低成本气体传感器检测精度。实验结果表明,COA算法可以有效提高GRU修正模型的学习性能和效率。在COA-GRU数据修正模型的处理下,SO2、CO、NO2、CO2检测浓度的平均绝对误差分别降低了72.0%、28.4%、29.6%、13.5%,该方法可以显著提高低成本气体传感器的检测精度,具有较强的可操作性,可应用于工业生产与环境监测等领域。