基于旋转变分模态分解的IMU角速度去噪算法

覃舒娴,覃晓兰,刘运毅

广西大学计算机与电子信息学院

0 引言

惯性测量单元(inertial measurement unit,IMU)主要用于物体三轴角速度与加速度的测量,在自动驾驶[1]、行人位姿估计[2]和姿态补偿[3]等领域有广泛应用。目前,主流姿态估计技术有卡尔曼滤波、粒子滤波、互补滤波以及深度学习等数据融合算法。这些算法以IMU的加速度和角速度为研究对象,经过对数据多角度、深层次和全方位的学习分析,从而获取准确可靠的姿态信息。

由于实际环境复杂多变,角速度在采集和传输过程中会受到噪声干扰。因此,如何最大程度消除角速度噪声,已成为IMU姿态估计中一项重要的技术。一般情况下,角速度噪声由确定性误差和随机噪声构成。针对由粗糙标定及加工误差引起的确定性误差,一些学者均对陀螺仪的零偏、标度因数和非正交误差等参数进行校准,但此方法受限于高精度和价格昂贵的特殊转台[4-6]。为摆脱对精密设备的依赖,邹泽兰等[7]先通过六位置法对加速度计和陀螺仪实现标定补偿,后对非正交误差建模标定,快速准确识别出各类误差。角速度的随机误差无明显变化规律,且处理过程繁琐复杂,其解决方法通常为误差补偿算法。H.Chen等[8]将IMU信号预先分割为小步长数据,输入符合噪声特性的卷积神经网络模型,取得了良好的滤波效果。张萌等[9]改进Allan方差法,与时间序列分析方法相结合,完成角速度随机误差模型的构造,显著提高了角速度估算精度和利用率。

与上述随机误差处理方法比较,小波变换、经验模态分解 (empirical mode decomposition,EMD) 、变分模态分解等算法无需模型辅助即可分离噪声。如M.Ding等[10]选用小波阈值滤除角速度的噪声,即使在动态环境中也表现出优异的噪声识别能力。鉴于小波基和阈值需遵循人工经验选择,李文华等[11]选择EMD算法与模态集合标准,成功获取原始角速度,然而EMD算法存在端点效应和边界效应等弊端。变分模态分解(Variational mode decomposition,VMD)的数学理论完善,兼具极强的自适应性、鲁棒性和稳定性,能够弥补上述两者算法的不足。J.R.Wei等[12]以VMD分解的子信号为基础,利用多尺度置换熵作为噪声的筛选标准,达成了正确区分噪声、真值及温漂的目标。

现有文献以及相关实验表明选择合适的变分模态参数,对角速度进行VMD分解后重构能消除信号的部分噪声。但是分别对角速度3个轴的信号进行VMD去噪会导致轴间去噪失衡问题,也就是3个轴的去噪性能不一致。为了进一步提高去噪能力,本文结合角速度的线性旋转变换和VMD的非线性重构构建去噪算法。

1 算法原理

1.1 变分模态分解

变分模态分解[13]是由K.Dragomiretskiy提出的一种非递归的信号分解方法,其原理是将信号分解成一系列不同频率和有限带宽的固有模态分量(intrinsic mode functions,IMF)。VMD算法由变分约束问题的建立和求解构成,其变分约束问题的建立公式如下:

(1)

(2)

式中:μk(t)为第k个模态分量;f(t)为目标信号;α为惩罚系数;ωk为模态分量的中心频率;δ(t)为单位脉冲函数;k为分解模态层数。

VMD算法本质上是约束变分模型对最优解的求取。二次惩罚系数确保了噪声情况下的信号重构精度;拉格朗日乘数保证了约束条件的严格性,两者联合可将约束变分问题变为非约束变分问题,得到的增广拉格朗日表达式如下:

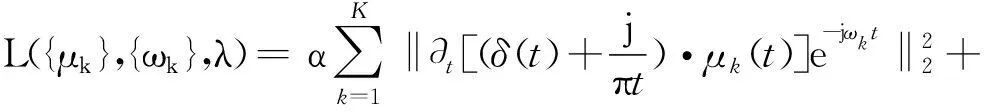
(3)

对于式(3)的求解,可引入交替方向乘子法,迭代搜索求取最优变分解,得到模态分量μk和中心频率ωk如下:

(4)

(5)

1.2 角速度的旋转变换

在IMU数据的描述情景中,载体坐标系(b)和地理坐标系(n)是常用坐标系。载体坐标系以载体质心为原点,方向分别为zb轴、yb轴和xb轴。地理坐标系以地球质心建立坐标系,其zn轴、xn轴、yn轴分别对应天、北、东方向。

IMU信号一般在载体坐标系中测得,载体坐标系会随载体运动而变化,此时的测量值等于原测量值与旋转矩阵的乘积。旋转矩阵是一个坐标系变换矩阵,描述三轴的旋转运动情况。可将一个完整旋转运动看作原坐标系沿三轴依次旋转,把这3个连续的旋转矩阵乘积表示最终的旋转结果,规定旋转次序为Z-Y-X,则坐标系的旋转变换公式如下:

(6)

处理数据时,把IMU芯片所处位置当作IMU坐标系的原点,角速度可近似于该坐标系内的单点向量,经坐标轴映射后得到虚拟三轴角速度。若对IMU坐标系进行随机旋转变换至其他坐标系,载体原各轴角速度会随之变化,包括虚拟三轴上的误差映射分量,该过程为角速度的三维旋转变换。从数学角度来看,由于角速度为三轴分量的线性叠加,角速度的旋转变换属于线性变换。

1.3 算法设计

VMD是面向一维数据的模态分解算法,具有非线性特征,所以尽管VMD参数完全相同,去噪后的三轴角速度仍会存在一定差异。当线性旋转变换后的三维角速度经VMD去噪回归原坐标系时,变换前后的IMF角速度(“IMF角速度”为经VMD降噪后的角速度,下文同理)和误差已不再相等。同时,因VMD的非线性特征,三维角速度的噪声保持相对独立。据此推测,若取多次旋转变换后的IMF角速度的均值为最终结果,可获得误差相对较小且均衡的三轴角速度,从而进一步提升VMD角速度去噪算法的性能。

(7)

(8)

多次重复上述步骤,将该过程产生的所有角速度的平均值作为最终去噪结果,以平衡三轴角速度间的误差。

考虑到上述去噪信号与真值信号仍存在一定差异,为此引入误差方向补偿使去噪结果进一步逼近真值。算法流程图如图1所示。

图1 算法流程图

2 实验结果及分析

本文算法以MATLAB2021b为实验平台,采用EuRoc数据集[14]完成实验,以验证算法的有效性。该数据集来源于微型飞行器的视觉惯性传感器。本文选用均方根误差(root mean square error,RMSE)作为衡量算法性能的评估标准。此外,需先采用龙格库塔法[15]通过姿态真值计算角速度真值,便于后续结果分析。

2.1 参数设置

2.1.1 VMD参数

在变分模态分解算法中,模态分解层数和惩罚系数需要人工经验预设,过大的模态分解层数会导致信号过度分解,进而引起模态混叠;过小的模态分解层数会使信号处于欠分解状态,不利于中心频率的正确分离。类似地,若惩罚系数选取不当,模态分量的带宽和保存过程也会受到影响。

下面通过实验研究该算法的参数调整方向。经多次实验,发现不同的惩罚系数并未引起角速度三轴RMSE的明显变化,且其最佳取值范围应为500～1 000。设定模态分解层数K=10,惩罚系数α=1 000,迭代停止参数ε=5×10-6,改变保留模态序列号th,计算经VMD处理后对应角速度的三轴RMSE,最终结果如图2所示。

图2 保留模态序列号(th)对角速度误差的影响

由图2可以看出,当保留模态序列号为2～4时,角速度三轴的RMSE都比其他保留模态序列号的小,表明角速度的噪声分量主要包含于低序列的IMF分量中。然而,当保留模态序列号大于4且不断增加时,该去噪算法性能不断恶化,原因在于包含角速度真值的分量被当作噪声错误剔除。

为了探寻K的合适取值范围,视具体情况设定模态序列号,依次调整K值,其他参数同上不变,采用VMD分解角速度。经多次试验发现当K>10时,角速度去噪性能差别不大,故仅展示K∈[2,10]的实验结果,如表1所示。

表1 不同K值去噪后的角速度RMSE

分析表1:一方面,K值与角速度去噪结果为正比例关系,且K为5～10时,角速度RMSE均值降低了60%～70%;另一方面,所提算法可最大程度去除噪声,进一步凸显了该算法的优越性和可行性。

2.1.2 角速度的旋转变换次数

根据1.2的理论分析,坐标系次数即为角速度的旋转变换次数,是一个较为重要的参数。维持其他参数与数据与上述相同,仅改变坐标系旋转次数研究该参数对角速度去噪效果的影响,最终实验结果如图3所示。

图3 坐标系旋转次数对角速度去噪的影响

由图3可以看出,由于旋转矩阵的随机性,当旋转次数较小时,各轴角速度的去噪效果产生失衡;但随着次数的增加,三轴角速度的误差逐渐变小且趋于稳定,旋转次数取值大于10时便可获取微小稳定的误差。

2.2 实验分析

参考2.1节实验结果,设置分解层数K=10,惩罚系数α=1 000,模态保留层数序号th=3,坐标系旋转次数为10,选用EuRoC数据集的MH_04_difficult和MH_02_easy序列,分别通过VMD和旋转VMD算法对角速度进行降噪,以比较两者算法的性能。为了便于区分,使用 “IMF角速度(R)”表示引入旋转变换后的VMD角速度去噪结果,如表2所示。

表2 不同序列去噪后的角速度RMSE

观察表2,VMD和旋转VMD算法,都显著减少了角速度中的噪声。与IMF角速度相比,经旋转变换优化的算法解算的三轴角速度误差水平量级相同,且平均误差距离更小,下降了约30%,充分证实角速度的旋转变换实现了对VMD解算的角速度的误差平衡。

为进一步验证本文所提算法的性能,分别选取卡尔曼滤波算法、神经网络算法[16]和本文算法作对比,结果如表3所示。

表3 不同去噪算法的角速度RMSE

因后面3个序列为神经网络算法的训练集,故无法参与该算法的角速度滤波。由表3可知,对比另外两种算法,本文算法的误差数值更小,RMSE降低了70%～85%,显然在角速度去噪上更具优势。综上所述,该实验充分证明了本文所提算法可有效降低噪声干扰,从而获得准确率更高的角速度。

3 结束语

围绕角速度噪声的时频域特性,提出了一种基于旋转VMD的角速度去噪算法,将惯性测量单元的坐标系旋转至虚拟坐标系,经VMD降噪处理,再转回原坐标系,多次重复转换后,求解所有角速度的均值。由于VMD重构的非线性特性,使得角速度在不同虚拟轴的旋转变换信号的VMD重构误差互相独立,从而多次旋转VMD去噪结果的叠加平均能有效抵消这些独立误差。经EuRoC数据集的多次实验验证,本文算法能够准确提取噪声和还原角速度,还可将角速度的三轴误差降至更为平均水平,证明了该算法的降噪优异特性,为IMU信号滤波提供了新思路。