高频响应悬臂梁单向阀动态特性研究

杨国来,杨鹏强,曹文斌,谢万耀,孙丽霞

(1.兰州理工大学 能源与动力工程学院,甘肃 兰州 730050;2.浙江大学 流体动力与机电系统重点实验室,浙江 杭州 310027)

引言

电液作动器作为航空航天、汽车和机器人应用中常规液压系统的潜在替代品是具有吸引力的。随着电气自动化和 IT 技术的发展,工业液压系统的集成变得更加容易且更具竞争力[1-2]。这些集成执行器消除了对液压管路的需求,从而实现了轻重量、高可靠性的线控系统[3]。

由于电动静液作动器具备的特点及优势,被广泛应用于伺服驱动工况,国内外学者也开展了对电静液作动器相关应用的研究。杜伟等[4]将电动静液作动器系统应用于船舶阀门启闭工况,综合考虑系统外部干扰力以及参数摄动情况,并将混合灵敏度鲁棒控制算法应用于电动静液作动器系统中,提高了该系统的位置跟踪性能。王岩等[5]针对电动静液作动器散热问题,提出了一种新的热力学建模方法,并建立三维热力学模型验证所提出方法的正确性。单向阀作为磁致伸缩泵中的核心部件之一,其动态性能对泵的可靠性、容积效率有着至关重要的影响[6]。早期的智能材料泵使用的市售球弹簧阀或定制的盘弹簧阀,其将泵送频率的峰值频率限制在100 Hz以下[7],限制了智能材料高频响的优点。在许多情况下,部分高频响液压系统的性能受到止回阀响应时间的限制。在阀门转换过程中,回流和节流会造成泄漏和能量损失。ZHU Y C等[8-9]设计了一种圆柱转阀配流的磁致伸缩电静液作动器,实验显示驱动频率为120 Hz时作动器的最大无负载输出流量为1.28 L·min-1。宋昀泽等[10]设计了一种基于主动阀配流的轴向双磁致伸缩泵驱动的电静液作动器,此主动阀将磁致伸缩泵在高频下吸入和排出的微量油液进行整流,进而获得大的流量输出,实验结果表明最佳驱动频率为180 Hz,在空载情况下输出峰值可达2.7 L·min-1。YANG X L等[11]设计了一种超磁致伸缩电液作动器,用悬臂梁阀片进行整合配流,利用压差打开和关闭阀片,该作动器在225 Hz 的驱动频率下,空载输出流量约为1.3 L·min-1,带负载质量超过14 kg。LARSON JP等[12]为作动器的压电泵设计一种新结构单向阵列式阀片,该新型阀片可以明显提升作动器的高频适应性,进而提高了作动器的饱和频率。然而相较于传统的单向被动阀,阵列式阀片的通流面积较小,这也将影响作动器的输出流量,所以这种阵列单向阀只有在高频驱动下才能体现出优势。王新峰[13]结合仿真软件ANSYS对压电泵上悬臂梁阀片进行固有频率的仿真分析,得到其在不同共振频率下的振型,选取合适的工作频率范围。闵为等[14]以超纯水隔膜阀为研究对象,结合理论分析及COMSOL模拟仿真方法,分析了超纯水隔膜阀使用寿命的影响因素,提出了超纯水隔膜阀的结构优化方案。GUO X Y等[15]分析了不同激励频率对压电悬臂板动力学响应特性的影响。

簧片式单向阀的弹簧和质量包含在一个元件中,因此与传统的阀瓣、提升阀或球型止回阀相比,簧片阀重量轻、结构紧凑。簧片阀相对低的质量使得该类阀很有期望用于在高频下操作的系统中,如高频液压回路、活塞泵和软开关模式回路和数字液压[16-17]等。在液压回路中运用簧片阀可以减少单向阀配流切换时间,以此来提高泵的整体效率和功率密度。高频率整流阀是目前可解决智能材料小位移[18]问题并开发适合于商业应用的大力、大冲程作动器的有效方式。惯性载荷、流体黏度、可压缩性也影响整泵的效率,限制了驱动致动器的高频响和总致动器输出功率[19-20]。

关于簧片式单向阀在液压系统中的建模和应用的公开研究很少。使用数值模拟,例如计算流体动力学CFD,对于包含止回阀的动态系统的设计和优化变得越来越可行。为了充分发挥磁致伸缩柱塞泵的高频优势,本研究将对配流阀对泵输出性能的影响进行研究提出了一种新型簧片阀结构。分析了不同频率,负载下阀的动态特性,对磁致伸缩泵向更高频率的发展具有重要意义。

1 磁致伸缩泵工作原理及结构

1.1 泵工作原理图

磁致伸缩泵由驱动部分和泵两部分组成,其结构示意图如图1所示。

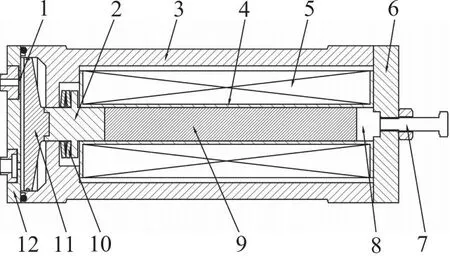
1.阀体 2.输出杆 3.外壳 4.线圈骨架 5.线圈 6.底座 7.预紧机构 8.滑块 9.磁致伸缩材料棒 10.碟簧 11.活塞 12.泵头

由信号发生器产生的电压信号通过功率放大器转换成线圈5的输入电流,当向线圈5施加交流电时,在磁致伸缩材料棒9的轴向方向上产生交变磁场,磁致伸缩材料棒9在交变磁场的作用下伸长和缩短,通过输出杆2和碟簧10直接带动活塞11进行往复运动,由泵活塞产生的小的高频流体脉冲用高频单向阀组1收集。腔内液体在高频单向阀组1的作用下配流,活塞在双向运动的过程中泵分别实现吸、排油。

1.2 单向阀工作原理

本研究提出的双瓣式单向阀如图2所示,簧片阀可以被视为在流体中振荡的悬臂梁。

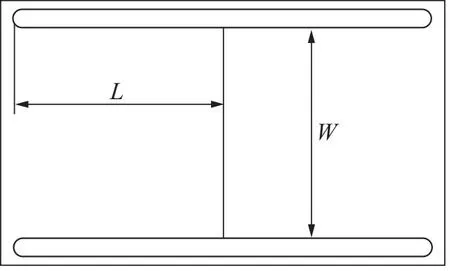
图2 阀片尺寸

阀瓣工作时被认为是长度为L、宽度为W、厚为h,有效质量为m的弯曲板,其一端(s=0处)被夹紧,虚线C是假定孔口面积的周长,而Wo是假定孔口面积的宽度,其是坐标s的函数,如图3所示。阀片的开启与关闭由阀片两侧的压差决定。对于阀片,较大的开度允许较小的压降穿过簧片,而较小的开度有助于防止簧片的塑性变形,并允许其更快地关闭,从而减少回流。

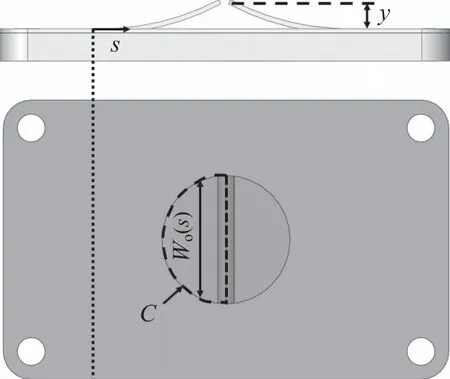
图3 簧片阀总成显示在全开位置

为了防止泵在带有负载的情况下,泵的出口阀外侧高压油作用于阀片使得阀片产生弹性变形,使得阀口反向打开导致油液反向流回泵腔,在阀座处设计了支撑梁,支撑梁位于阀口的直径上,在预期的最高负压差下为簧片提供足够的支撑,降低其应力和变形。梁的侧面形状为流线型结构,阀座材料采用结构钢,如图4所示。

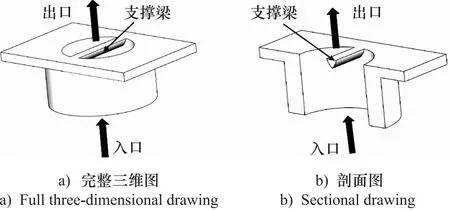
图4 带有支撑梁的阀座三维图及剖面图

为了确保阀片在工作中不发生任何塑性变形,对阀片进行了应力分析。考虑了泵的最大阻塞压力为10 MPa。使用COMSOL Multiphysics开发了有限元模型,以分析阀片所受应力,优化设计尺寸以将应力减小到允许的水平。有限元计算结果如图5所示,可知所受最大应力为123 MPa,而铍青铜的屈服强度为1000 MPa,故满足强度要求。

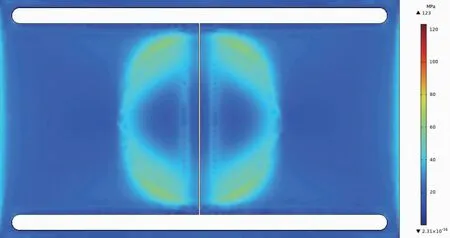
图5 阀关闭时的设计应力

2 数学模型

2.1 阀片动力学模型

阀片上的作用力如图6所示,吸油阀和排油阀在实际工作过程中都可以看作为单自由度的弹簧-质量-阻尼系统。随着入口压力增大,介质作用于阀片上的力大于阀片弹簧力与出口侧介质作用力的合力,单向阀开启。随着入口压力减小,阀片弹簧力与出口侧介质作用力之和大于介质作用于阀片上的力,阀片在自身弹簧力的作用下实现反向截止密封,单向阀处于关闭状态。

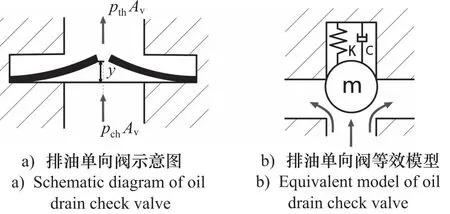
图6 双瓣悬臂梁单向阀原理图

在建模过程中,假设阀片具有Euler-Bernoulli梁理论性质,即在无修正情况下不考虑梁剪切形变,且忽略其转动惯量,承受分布压力载荷Δp,在时间t时,沿着簧片位置s的位移ξ由下式给出:

(1)

式中,h——阀片厚度

R——阀片每单位长度的内部阻尼系数

E——阀片材料的杨氏模量

I——材料的转动惯量

Δp——阀两侧压力差

如果假设簧片的位移可以表示为相对于初始簧片挠度y0的尖端位移y的函数,则:

ξ(s,t)=ψ(s)(y(t)-y0)

(2)

其中,模式函数ψ是通过尖端开口归一化的簧片位移,且ψ(L)=1。

在排油阶段,吸油单向阀的位移为0,且阀片内侧压力大于腔外压力。簧片运动方程,相对于簧片尖开口y(定义为簧片座和簧片尖之间的距离),作为时间的函数,由下面的常微分方程给出:

(3)

式中,m——阀片有效质量

y0——阀片初始尖端挠度

C——系统阻尼系数

γ1——第一模态函数参数

K——阀片刚度

pch——泵腔压力

pth——阀片外侧压力

Av——阀片面积

X——压力载荷乘数

第一模态函数参数说明了阀片的偏转形状,以便在一个单一的点,即尖端模拟簧片运动。使用集总参数模型,该模型不考虑作用在阀片上的非均匀压力分布,仅利用阀内测和外侧的某个位置处的压力信息建立阀动力学建模:

(4)

2.2 流量模型

通过簧片式单向阀的流量计算为阀片与阀座之间的孔口流量和由阀片运动排出流体速率的总和。阀座孔口流建模为准稳态,除了阀座孔口流动之外,与开/关阀不同,当阀片工作偏转时,阀片扫掠排出一定体积的流体,该体积为尖端开口的函数,其中AQ是每个尖端开口移位的流体体积。因此,通过阀的流量Q的函数计算为:

(5)

式中,Cd——孔口流量系数

A——阀孔口面积

ρ——流体密度

u——阀片尖端速度

通过考虑阀座和阀片之间的最小流道来计算阀座的孔口面积。该区域的周界被假定为虚线C,如图2所示,将该曲线投影到阀片上以创建相应的闭合曲线。由这两条曲线包围的面积是孔口面积。对曲线C附近的模态函数进行积分,得到每单位阀片叶尖开度的孔面积A,因此孔口面积:

(6)

表1 阀片模型参数

每单位阀端开口由簧片排出的流体体积由下式给出:

(7)

2.3 单向阀的频率响应

超磁致伸缩泵在某一个频率范围内工作,该频率除了受流体黏度和流场结构的影响,很大程度上也依赖于单向阀自身的响应速度。阀片结构参数是响应阀频率的主要因素,在无阻尼情况下,悬臂梁单向阀的固有频率可表示为:

(8)

式中,Av——阀片面积

ρv——阀片密度

泵中柱塞运动的频率不超过阀片自身谐振频率时,系统能够进行正常吸排油。在超磁致泵的工作频率下,阀片的一阶振型尤其重要。阀片的一阶谐振频率为:

(9)

由式可知,阀的一阶谐振频率与阀片厚度h成正比,与L的平方成反比,而阀片材料的杨氏模量和密度由材料自身决定,所以,增大阀片厚度,即可提高单向阀的响应频率。仿真计算得出阀片第一模态为2342 Hz,其他模式的频率明显更高,不会影响阀门性能。

对于在液压油中工作的阀片,阻尼由簧片的内部阻尼和流体阻尼共同构成,所述内部阻尼是因为阀片工作时在变形期间耗散能量,所述流体阻尼是因为簧片对流体做功。如果假设流体为黏性流体,则阻尼系数可以被定义为包括串联的2个阻尼源。此外,阀片附近的流体随着阀片加速,产生附加质量效应。黏附在阀片周围的流体会增加阀片的重量,降低了阀片的响应频率,与真空中的固有频率fv相比,流体中减小后的一阶固有频率ff为:

(10)

式中,Ma——板上附加油液质量

簧片式单向阀为悬臂梁结构,附加于阀片上的附加质量等于阀片面积所扫掠腔体内的流体质量,附加质量Ma为:

Ma=0.25ρπW2L

(11)

3 数值模拟分析

3.1 模型假设

使用多物理场软件COMSOL基于单向阀的几何形状建立了流固耦合模型验证单向阀在正弦信号下的响应性。工作介质如表2所示,入口是幅值为60 kPa正弦压力信号,出口为0压力出口。因为发现在最高工作流体速度下的雷诺数低于500,所以假设流动为层流。此外,为了计算简单,假设流体是不可压缩的。图7示出了对阀的仿真进行建模的几何形状。由一个2D轴对称模型探索阀的流动特性,将阀近似为阀瓣的2D是合理的,因为阀口处的大部分压降发生在阀座下方。该仿真模型工作介质参数信息如表2所示。

表2 工作介质参数

图7 使用COMSOL进行有限元建模的几何图形

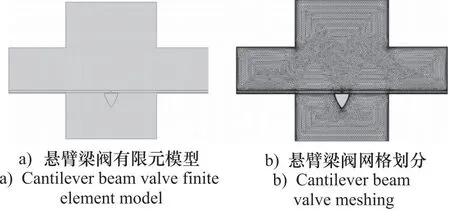
图8 单向阀流域网格模型图

3.2 网格划分

由于流阻较为复杂,因此采用非结构网格对单向阀流域进行网格划分,针对复杂结构处进行网格加密,以提高准确性。由于仿真过程中阀片位移相对网格大小较大,故需要使用重构网格。

3.3 监测点设置

为了准确研究两种阀的响应特性,如图9所示,在阀片上分别设置监测点,为了在同一幅图中更好的对比两处的位移变化,单瓣式单向阀等效开口位移监测点位于阀口中心A处,双瓣式单向阀开口位移监测点位于阀片末端B处。

图9 两种单向阀开口监测点设置

3.4 动态响应仿真分析

1) 出口压力为 0 时阀动态特性

由于磁致伸缩材料作为活塞动力源可以适应很高的频率响应,因此悬臂梁阀的动态响应将影响泵的输出性能,不同频率作用下,阀片开口位移随压差信号变化的瞬态曲线如图10所示。

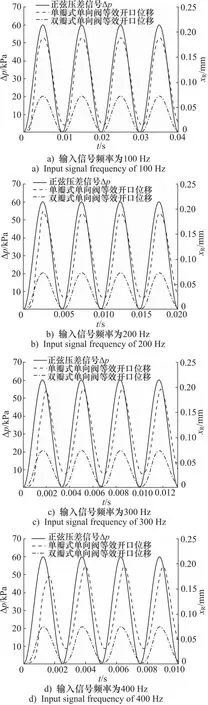
图10 不同频率正弦压差作用下两种阀片的动态特性

根据图10,随着频率的增加,单瓣式阀片和提出的双瓣式单向阀的等效开口位移都随压差信号近似呈正弦变化,且随着频率的增大,阀片的开启与关闭都出现了越来越明显的滞后,压差到达下止点之后,在压力迅速增加之前会存在轻微延迟,这是由阀片延迟开启导致的腔内油液被压缩所导致,关闭的延迟使阀口压力保持在超过压差下止点的负载压力,从而高压油回流到柱塞腔中。

两种阀不闭合阀口位移占最大开口位移百分比计算结果分别如表3和表4所示。

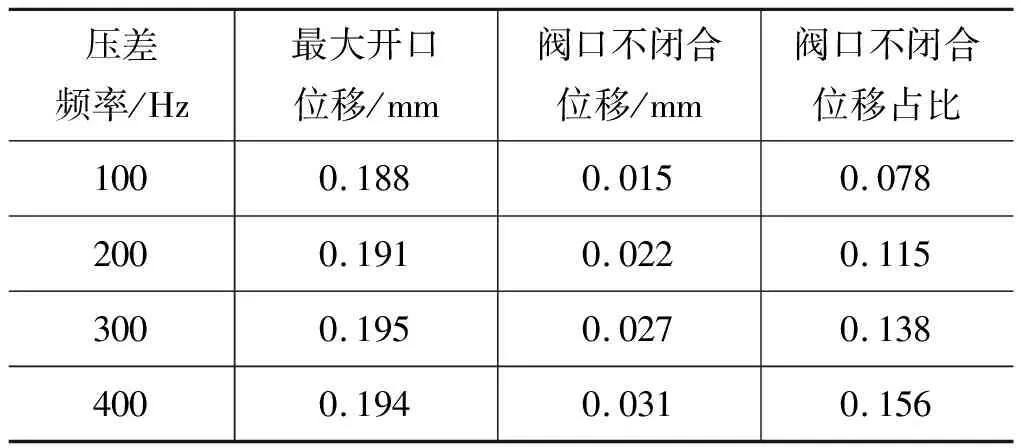
表3 不同开启频率下单瓣式单向阀阀片等效开口位移

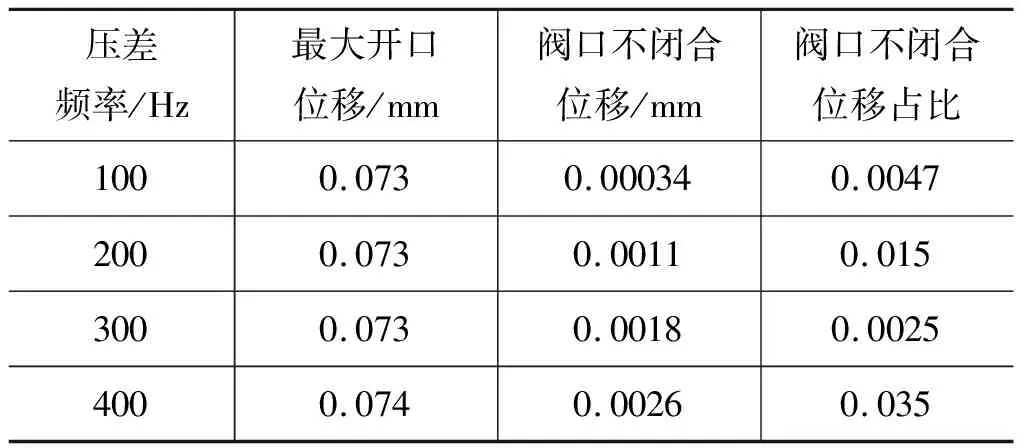
表4 不同开启频率下双瓣式单向阀阀片等效开口位移

根据表3和表4,随着频率增大,在压差信号下止点处,阀片距离原点(阀片未开启时的位置)的位移即不闭合情况也随着频率的增大而增大,输入压差信号频率每增加100 Hz,阀口不闭合位移增加2.1%,这说明单向阀不能关闭,配流时柱塞运动与吸排油单向阀的运动逻辑关系发生错位,导致高低压油腔互相连通,泵工作时油液产生回流倒灌现象,造成能量损失和工作效率下降,影响泵在高频时输出性能,磁致伸缩材料的高频响应特点不能被较大化利用。双瓣式单向阀的频率响应性和阀口关闭性能相较于单瓣式单向阀都更好,输入压差频率每增加100 Hz,阀口不闭合位移增加1%,可以更好适应磁致伸缩微泵的高频输出,提高泵的效率。

通过图9可以看出,单瓣式单向阀的阀口位移监测点位于阀片中间,由悬臂梁挠曲线方程知,梁的变形是非线性的,在阀不关闭的情况下,阀开口端部B处的实际开口位移大于监测点A处位移的2倍,倒灌现象更严重。当频率为400 Hz时,阀不关闭位移已占最大开口位移的15.6%,此时对泵的配流和效率已产生很大影响。

2) 不同出口压力下阀动态特性

对频率为200 Hz的信号进行加载,出口压力分别为10,20,30,40 kPa,对阀的响应进行分析。

从图11可知,随着出口压力的上升,阀开口量也越来越小,出口压力为10 kPa和20 kPa时,阀口不关闭的情况还存在,这依旧会导致液体的回流,影响泵的效率。在出口压力为30 kPa的情况下,阀的位移已经不是明显的正弦变化,这是由于在CFD仿真时,流体计算域要保持连续性,以生成网格,如图7所示,阀片和阀座存在间隙,入口压力未达到30 kPa时,30 kPa的出口压力会在这个间隙对阀产生压力,开启阀口。在出口压力压力40 kPa 时,当入口压力增加到大于40 kPa 时,阀才会被20 kPa的压差打开,故位移较小。图11中,阀位移正弦曲线每个周期前端的小位移开启主要由入口压力和出口压力压力共同产生。

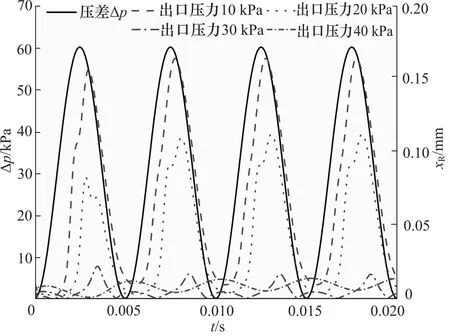
图11 单瓣式单向阀200 Hz频率下在不同出口压力时阀的响应

对双瓣式单向阀进出口为200 Hz的信号进行加载,出口压力分别为10,20,30,40 kPa,对阀的响应进行分析,如图12所示。

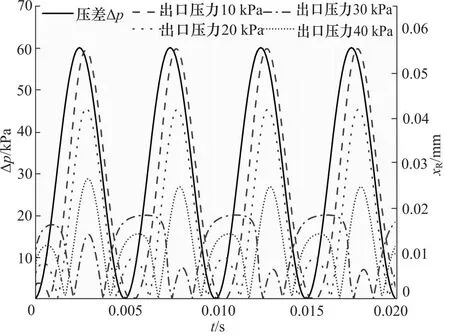
图12 双瓣式单向阀200 Hz频率下在不同出口压力时阀的响应

从图12可以看出,双瓣式单向阀阀口在不同的压差下都可以完全关闭,可适应更大压差,且阀的位移都是近似正弦变化。随着出口压力的上升,出口压力对阀口开启位移的影响相对单瓣式单向阀较小。在30 kPa 出口压力下,阀入口压力降低时,阀口位移反而增大,这是出口压力从微小仿真缝隙回流所导致。在出口压力40 kPa时,阀的开口等效位移很小,主要由40 kPa的出口压力与入口压力之差打开。图12中,阀位移正弦曲线每个周期前端的小位移开启主要由入口压力和出口压力共同产生。

从以上分析可知,出口压力影响阀片位移,且对单瓣式单向阀影响更大,但对阀片的响应性不产生影响。双瓣式单向阀有更好的高频跟随性,可以使得磁致伸缩材料的高频性能在液压领域中得到更好的应用。

4 结论

(1) 提出了一种结构简单、紧凑的被动双瓣式单向阀。将已有单瓣式单向阀与本研究提出的双瓣式单向阀的高频响应进行比较,结果得出单瓣式单向阀随着输入压差频率的增加其动态响应性变得越来越差,频率每增加100 Hz,阀口不闭合位移增加2.1%,这说明单向阀在高频驱动下不能关闭,配流时单向阀的运动逻辑关系发生错位,高低压油腔是互相连通的,油液产生回流倒灌现象,配流效率降低,这是导致磁致伸缩泵在高频驱动下输出性能下降的原因之一。而双瓣式单向阀频率每增加100 Hz,阀口不闭合位移增加1%,且高频跟随性更好,这可以使双瓣式单向阀在高频系统中得到应用;

(2) 在出口带有出口压力的情况下,两种阀的响应性都不受频率变化的影响,单瓣式单向阀和双瓣式单向阀都会随着出口压力的增加产生阀片开度减小的情况,但双瓣式单向阀随出口压力的增大受影响较小。提出的双瓣式单向阀在高频液压回路中的应用具有实际意义。