基于新合作模式的逆向物流演化博弈分析

栗治杰,贾东水

(河北工程大学管理工程与商学院,河北 邯郸 056004)

随着新时代中国绿色发展的不断推进,逆向物流逐渐受到社会关注。不同于正向物流的是,它涉及各类废旧产品的回收、分类、再制造和绿色处理等环节。而产品回收作为逆向物流的起点,具有高度复杂性,因此被认为是逆向物流中的首要任务。

逆向物流通过回收和再利用废弃产品和材料,实现资源的再循环利用。在这一背景下,许多研究致力于构建高效的逆向物流网络[1-2]、制定相应的管理策略[3]以及监督机制[4],以促进废弃物的可持续处理[5-6]和资源的有效利用[7],这样不仅有助于减少环境污染,还为企业创造了经济价值[8]。然而,在这个领域中,消费者角色[9]和积极性[10]一直是一个备受关注的话题。消费者作为逆向供应链的重要参与者,其行为和偏好对整个逆向物流系统的演化和效果产生深远影响[11]。因此,研究消费者在逆向供应链中的参与方式以及其对逆向物流决策的影响,成为当前研究的一个重要方向。

现有研究成果主要集中在政府行为对逆向物流合作的影响[12-13],对消费者影响合作的研究较少。作为使用逆向物流系统的重要参与主体,消费者行为对合作模式的认可程度是促成合作的关键。针对现实情况中物流终端和零售商店选址情况类似的背景,提出一种创新的合作模式,为消费者带来便利。利用零售商现有的场所,把待取的快递陈列在商品货架上,实现零售商为快递提供暂存点,以此吸引更多消费者进入商店,并引导消费者在店内收集物流包装,物流企业回收包装并向零售商支付货架使用费用的新经营模式。

本文考虑到参与包装逆向物流双方的有限理性,并分别建立在合作初期消费者被动参与,对合作经营模式认识较少,不对系统产生反馈时的模型和在合作成熟期,消费者认识到合作经营的便利性,主动参与包装逆物流并对系统产生反馈时的演化博弈模型,旨在分析影响双方合作的因素以及消费者在其中扮演的角色,从而对完善包装回收产业提出合理的建议。

1 消费者被动参与的演化博弈模型

以消费者的参与作为切入点,零售商和物流企业各自占领市场优势和物流优势,探讨逆向物流在消费者“被动参与”和“主动参与”两种模式下双方的动态演化策略。由于零售商业务不涉及物流过程,且回收主要发生在零售商一方,因此物流企业在合作中需要优先考虑零售商合作意愿。基于以上考虑,建立演化博弈模型。

1.1 演化博弈模型假设

假设1:零售商和物流企业都是复杂利益群体的集合,每个个体都有自己的利益和目标,所以每个单独个体都有选择合作或者不合作的机会。假设其中零售商选择合作的概率为x,则采取不合作的概率为1-x;物流企业选择合作的概率为y,采取不合作的概率为1-y。

假设2:考虑到现有运营情况为双方都未合作,所以设置在演化过程中,当双方都选择不合作时,双方的营运模式不变,以此作为演化过程中的比较基准,利润收益保持现状,此时零售商的利润为T1,物流企业的利润为T2。

假设3:当双方都选择合作时,此时场景为(x,y),零售商承担物流终端业务,消费者寄取商品等需求使得零售商门店客流量增加,假设利润增加率为α;零售商合作回收物流包装使物流企业物流成本降低,整体利润增加比率为β;以零售门店为物流终端时,物流企业减少了开设物流终端的费用Q,零售商开展合作所需要的成本P由物流企业承担;合作的双方需要共同承担合作中包括沟通、运营等日常费用,假设零售商承担R1,物流企业承担R2。其中αT1-R1+P>0,βT2-R2-P+Q>0,即在双方选择合作后,各自增加的利润必须大于各自支付的费用。

假设4:当有部分零售商或物流企业选择合作后,未选择合作的一方将陷入市场竞争中的劣势。因为合作的物流企业通过降低成本获得了更多的资金用于发展,同时参与合作后的零售商吸引了更多的人流。在此处满足购物需求的消费者也不会再去其他零售商处消费,所以未合作的零售商和物流企业会分别得到利润损失S1和S2。假设此时市场竞争不变,这些利润分别由选择合作的零售商和物流企业获得,并各自承担合作需要的成本R1和R2。

1.2 模型构建

在消费者消极参与,结合上文假设,可得双方的博弈支付矩阵,见表1。

表1 零售商与物流企业的收益矩阵

由表1可以得出零售商选择合作时的期望收益E11为

E11=y[(1+α)T1-R1+P]+

(1-y)(T1-R1+S1)

(1)

零售商选择不合作时的期望收益E12为

E12=y(T1-S1)+(1-y)T1

(2)

(3)

进而可构建零售商复制动态方程为

x(1-x)[y(αT1+P)-R1+S1]

(4)

E21=x[(1+β)T2-R2-P+Q]+

(1-x)(T2-R2+S2)

(5)

E22=x(T2-S2)+(1-x)T2

(6)

(7)

y(1-y)[x(βT2-P+Q)-R2+S2]

(8)

1.3 系统1的稳定性分析

由式(4)和式(8)组成的零售商-物流企业演化博弈系统1,该系统描绘了零售商和物流企业在合作过程中的动态博弈过程。令F(x)=0,F(y)=0,可以得到该博弈的稳定状态,分别为x=1,x=0,y=(R1-S1)/(αT1+P),和y=1,y=0,x=(R2-S2)/(βT2-P+Q),这3个稳定状态代入复制动态方程的导数小于0时,为演化稳定策略。

易得,当x=1时,∂F(x)/∂x=-[y(αT1+P)-R1+S1],因此当y>(R1-S1)/(αT1+P)时,x=1是演化稳定策略,说明物流企业选择合作策略的概率y在较高范围[(R1-S1)/(αT1+P),1]内时,零售商的动态演化会向合作趋近。

当x=0时,∂F(x)/∂x=y(αT1+P)-R1+S1,因此当y<(R1-S1)/(αT1+P)时,x=0是演化稳定策略,即物流企业选择合作的概率y在较低范围[0,(R1-S1)/(αT1+P)]内时,零售商的选择会向不合作演化。由此可得,零售商的选择策略会根据物流企业的选择进行动态调整。

当y=1时,∂F(y)/∂y=-[x(βT2-P+Q)-R2+S2],因此当x>(R2-S2)/(βT2-P+Q)时,y=1是演化稳定策略,说明当物流企业知道零售商有合作意愿时,选择合作的概率x在较高范围中[(R2-S2)/(βT2-P+Q),1]时,物流企业的策略也会向合作趋近。

当y=0时,∂F(y)/∂y=x(βT2-P+Q)-R2+S2,因此当x<(R2-S2)/(βT2-P+Q)时,y=0是演化稳定策略,即当物流企业得知零售商合作意愿较低,合作概率x在较低范围中[0,(R2-S2)/(βT2-P+Q)]时,物流企业的动态策略也会向不合作趋近。

由此可得系统1的演化均衡点为A(0,0)、B(0,1)、C(1,0)、D(1,1)、E[(R2-S2)/(βT2-P+Q)、(R1-S1)/(αT1+P)]。进一步根据复制动态方程可以得到系统1的雅可比矩阵J为

(9)

根据演化博弈收敛条件计算矩阵的行列式和迹为detJ=A11A22-A21A12,trJ=A11+A22。若均衡点对应的雅可比矩阵的特征根都为负,即同时满足detJ>0和trJ<0,则该点为演化博弈的稳定策略(ESS)。代入均衡点后得到行列式和迹,见表2。

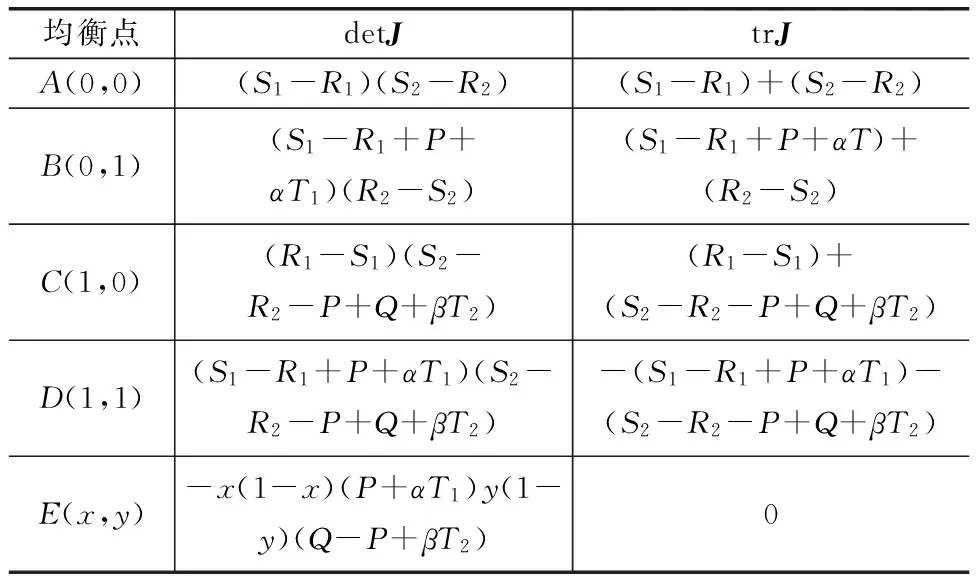
表2 各点的行列式和迹

分别讨论S1和R1、S2和R2的大小关系所影响系统1的演化稳定性,结果见表3～表6。

表3 当S1-R1>0、S2-R2>0时系统稳定策略

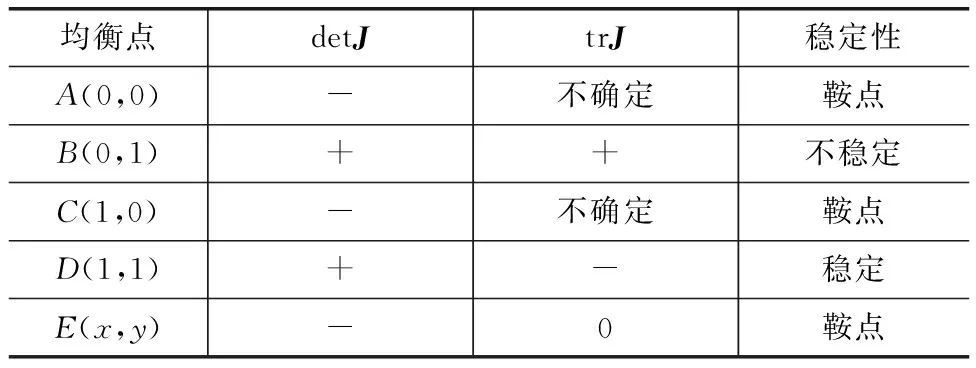
表4 当S1-R1>0、S2-R2<0时系统稳定策略

表5 当S1-R1<0、S2-R2>0时系统稳定策略

表6 当S1-R1<0、S2-R2<0时系统稳定策略

1.4 演化结果分析

根据表3～表6可知,共同的演化稳定策略是D(1,1),即双方都选择合作。当S1-R1>0、S2-R2>0时双方中未参与合作的一方所收到的利润损失都大于各自合作所支付的成本,并且合作做需要的费用也可以用合作后额外的收益来支付,因此双方都会倾向于合作;当S1-R1>0、S2-R2<0或S1-R1<0、S2-R2>0时未合作的双方有一方的利润损失少于其所需支付的合作费用,此时,选择合作的一方收获的利润超过了合作所需费用,所以始终有一方存在合作意愿,因此另一方只能选择参与合作减少利润损失;当S1-R1<0、S2-R2<0时双方不合作时的利润损失都较少,所以双方都有可能选择合作或者不合作,其演化相位图如图1所示,双方选择合作的概率由图中ABEC和BECD面积所决定,当E点落入直线BC下方时ABEC的面积小于BECD的面积,双方的策略倾向于不合作,反之则倾向于双方合作。当E点落在直线BC上时,双方选择合作或不合作的概率相等。

图1 演化博弈相位图

2 消费者主动参与下的演化博弈模型

2.1 演化博弈模型

对消费者而言,在双方合作初期“零售+取件”的合作模式是全新的运营方式,在未出现这种合作时,消费者的默认预期是去单独的店里取件或者购物,因此合作的运营模式对消费者的预期未造成影响,所以在此期间消费者是被动地接受此类合作,并不对合作双方造成影响。但当双方保持长久合作,消费者体会到一店两用的便利后,会主动参与到双方合作中来,使得物流包装更多地被回收。此时零售商和物流企业双方合作会额外增加G1和G2的收入,并且零售商因为回收了包装垃圾美化了环境,并为消费者提供便利从而使消费者对其好感提升了f。如果只有一方合作,此时未合作的零售商或者物流企业会收到因为降低了消费者的心理预期,未能提供便利等因素降低了D1和D2的收入。其余假设均与系统1一致。

2.2 零售商-物流企业演化模型建立

模型下零售商与物流企业的博弈支付矩阵见表7。

表7 零售商与物流企业的收益矩阵

E31=y[(1+α)T1-R1+P+

G1+f]+(1-y)(T1-R1+S1)

(10)

E32=y(T1-S1-D1)+(1-y)T1

(11)

(12)

进而得到零售商的复制动态方程为

P+f+D1+G1)-R1+S1]

(13)

E41=x[(1+β)T2-R2-P+Q+G2]+

(1-x)(T2-R2+S2)

(14)

E42=x(T2-S2-D2)+(1-x)T2

(15)

(16)

进而得到物流企业的复制动态方程为

P+Q+D2+G2)-R2+S2]

(17)

2.3 系统2的稳定性分析

由式(13)和式(17)组成演化博弈系统2,此时令F(x)=0,F(y)=0,可以得到系统2的演化均衡点为A(0,0)、B(0,1)、C(1,0)、D(1,1)、E[(R2-S2)/(βT2-P+Q+D2+G2),(R1-S1)/(αT1+P+f+D1+G1)]。

计算复制动态方程的偏导数得到系统2的雅可比矩阵J,代入各均衡点得到detJ和trJ,见表8。

(18)

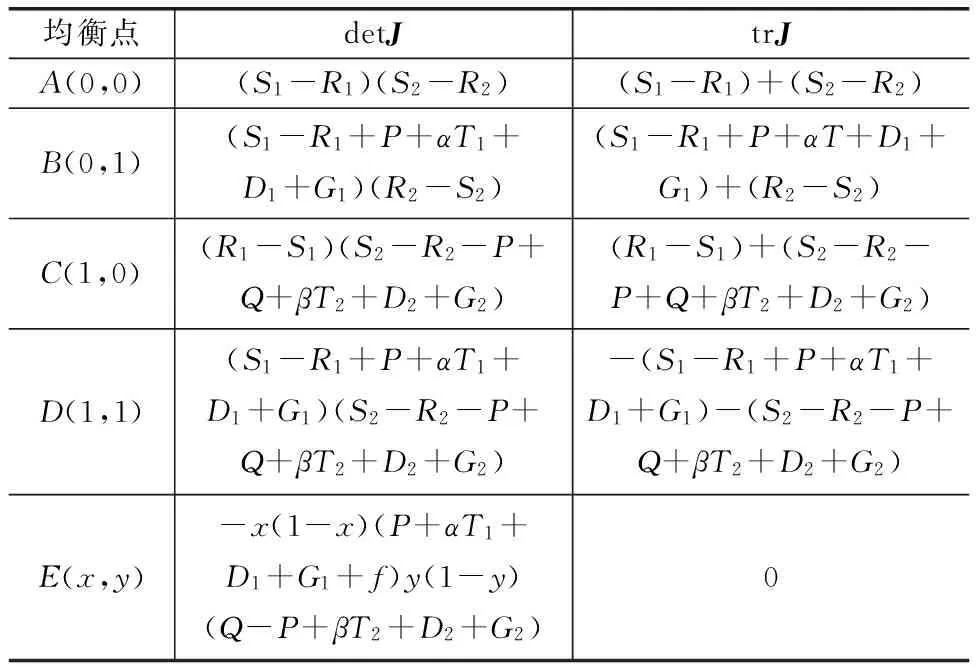
表8 系统2的行列式和迹

根据演化博弈收敛条件即detJ和trJ的正负,判断演化博弈稳定点,得到当S1-R1<0、S2-R2<0时,系统2的稳定点是A(0,0)和D(1,1);当S1-R1>0、S2-R2>0时系统2的稳定点是D(1,1);当S1-R1>0、S2-R2<0或S1-R1<0、S2-R2>0时系统2的演化博弈相位图和系统1类似,双方合作的概率由E点的位置决定。

3 模拟仿真

假设当双方都未合作时,零售商的利润为300,物流企业的利润为1 000,合作后双方利润分别提升10%和5%。双方共同承担的合作费用中零售商承担R1=30,物流企业承担R2=20,物流企业减少的开设物流终端费用Q=50,使用零售商平台需要支付的费用P=30。在合作模式成熟后消费者主动参与时,合作的零售商和物流企业分别增加收入G1=10和G1=20,零售商的好感提升f=3,未合作的双方减少D1=5和D2=10的收入。

3.1 数值模拟分析和比较

在S1-R1<0、S2-R2<0时,取S1=5,S2=10,演化结果如图2所示,双方的合作概率在[0,1]区间内变化,从0开始以0.1为步长演化,从图2中可以发现在系统1和系统2情况下,零售商和物流企业都会产生两个稳状态,即两个稳定策略点(0,0)和(1,1),和演化相位图类似,可以发现在系统2中延缓均衡点E更接近原点,即决定双方合作的面积更大,说明在双方长期合作,消费者感到便利积极参与合作后,可以更明显的推动这种合作运营模式的发展。

图2 系统1、系统2演化轨迹图

在S1-R1>0、S2-R2>0时,取S1=40,S2=30,演化结果如图3所示,系统1和系统2 都有共同的稳定策略点(1,1),说明在未合作的双方利润损失较大时,零售商和物流企业都倾向于选择合作。当未合作的一方利润损失较大,一方利润损失较小时,演化情况与此类相似。

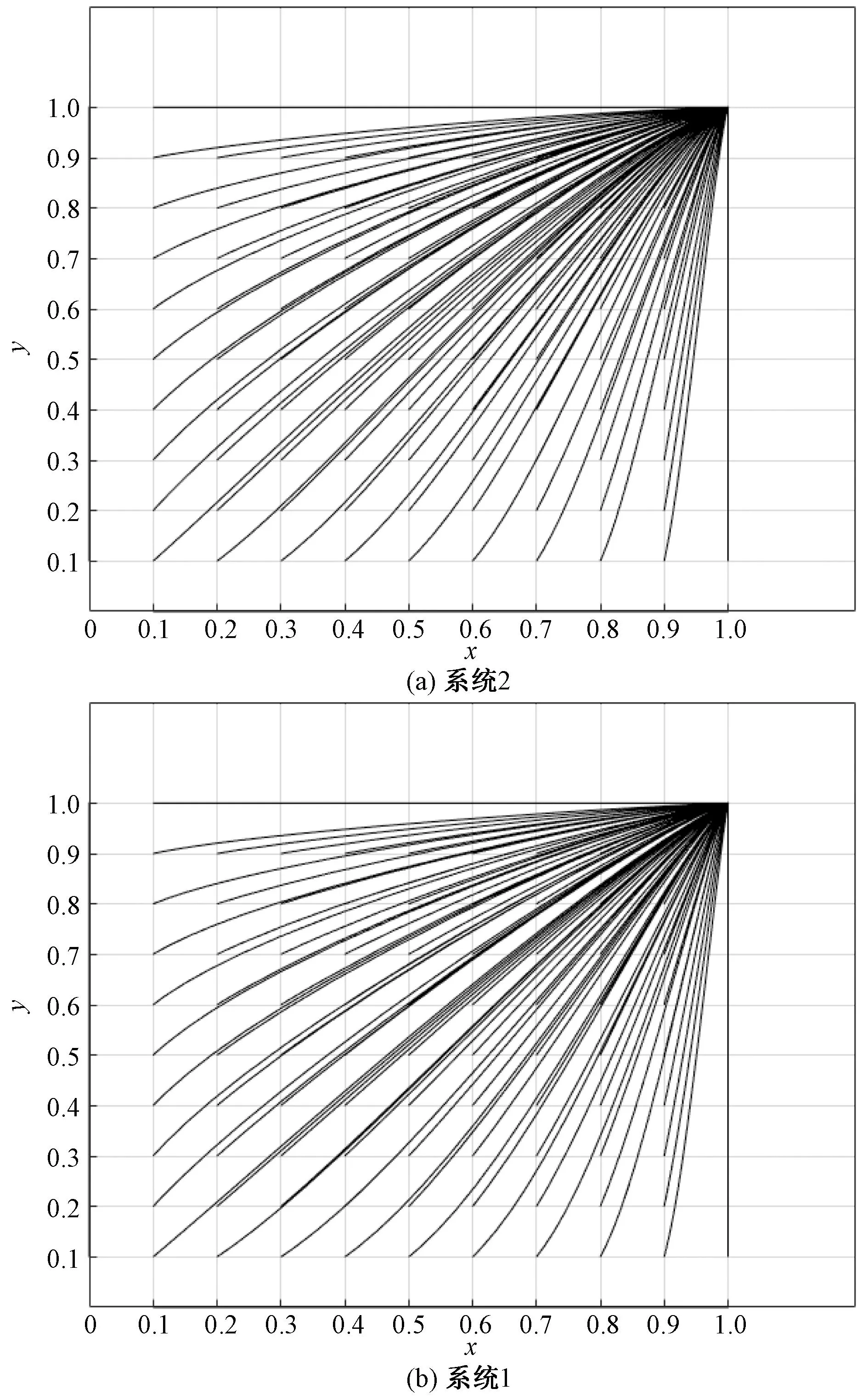
图3 系统1、系统2演化轨迹

3.2 数值影响

在双方不参与合作的利润损失较小时,即在S1-R1<0、S2-R2<0时,在系统1和系统2分使S1从(5,10)中取值,S2从(10,15)中取值,假设双方合作概率从0.1开始演化,发现当S1和S2增大时,两个系统虽然存在两个稳定点,但均以更快的速度趋近于稳定点(1,1),说明利润损失可以明显影响双方的决策选择,利润损失的扩大会使得双方急于寻求合作机会。此时演化稳定状态与演化均衡点E的位置有关,随着S增大,化均衡点E也越来越接近原点,双方合作的概率也越来越大。同时在S1与S2相同的情况下,对比系统1和系统2的演化图可以发现在系统2中的E点更接近原点,即当双方保持合作之后,消费者的影响可以进一步促进双方的合作。在此情况下,增大物流企业所需支付的费用P,发现可以进一步增加双方合作的概率。

当至少一方的利润损失较大,即未合作的一方所受到的利润损失S大于合作所需支付的费用R时,发现随着损失较大的一方的利润损失进一步亏大,系统同样以更快的速度趋近于稳定点(1,1),说明利润损失较大时双方都急迫的寻求弥补亏损,所以双方合作的概率更大。

相反当合作双方的合作费用R1和R2在(10,40)内增加时,系统的演化均衡点E会随着R的增加距离远点越远,这表明双方合作的概率在降低,即合作费用会影响双方合作的积极性,合作费用越低,双方合作的积极性越强。

当考虑消费者对合作双方的反馈后,原假设情况不变,使G1和G2在(10,30)内取值,f在(0,10)内取值,D1和D2在(5,25)内取值,发现随着G、f、D的增加演化均衡点E不断靠近原点,双方合作的倾向越来越强,说明消费者对合作运营模式的反馈可以有效促进双方合作的趋势,消费者越积极参与,主动配合合作,双方合作的积极性也越强,合作的概率也越大。

4 结论与启示

针对物流包装回收业务,开发了一种创新的一店两用的运营模式,并且考虑到参与的双方,零售商和物流企业的有限理性,以消费者对双方合作模式的反馈作为切入点,分别建立了消费者被动参与,不对合作做出反馈和消费者主动参与,对合作造成影的两个演化博弈模型,并对此进行数值模拟仿真,根据演化博弈均衡点位置分析双方选择的决策,主要得到如下结论和启示。

(1)无论是消费者对双方合作的运营模式是否造成影响,在任意一方因未参与合作造成的利润损失大于自己所需要支付的合作成本后,双方经过在市场的不断演变,最终都会选择双方合作。当较大的利润损失出现后,经营者会急迫地弥补损失,从而有较高的意愿参与合作。

(2) 无论是消费者对双方合作的运营模式是否造成影响,在因未合作而产生的利润损失较小时,演化模型会存在两个稳定策略(0,0)和(1,1),即双方同时选择参与合作或者不合作,合作的概率由演化均衡点的位置决定。在出现的利润损失较小时,经营者弥补亏损的动机较小,合作意愿并不强烈,因此较小的利润亏损,对双方选择合作策略起不到理想效果。与此同时,通过分析当S逐渐增大,R逐渐缩小或者物流企业所需要支付的成本P增大时,可以有效地提高双方合作的概率。即双方通过优化沟通渠道、经营策略或物流企业主动沟通、承担成本可以让让合作经营模式快速上线。

(3)在考虑消费者在合作中的反馈后,一店两用的运营模式给零售商带来的利润增加率的扩大,和物流企业通过回收削减成本的增加,都能有效地提高双方选择合作策略的概率。在此时,零售商经营者通过主动引导消费者处理包装垃圾,加大物流包装回收的力度,可以有效改善环境现状。

(4)当消费者积极参与包装回收的合作模式后,演化模型以更快的速度收敛,说明消费者的参有效地促进和影响了双方合作的趋势,对形成包装回收的成熟产业链有着积极的推动作用。物流企业应当积极主动沟通,在经营合理的情况下在合作前期承担更多的成本,以促进合作模式尽快上线。目前,有关包装回收的行业准则和相关法律法规还有待完善。因此消费者通过自己在市场操作中的选择可以加快推动相关体系的完善,打破现有包装回收的瓶颈。