基于RMT-CNN 的电网短路故障定位研究

2024-04-24刘义艳郝婷楠张伟

北京理工大学学报 2024年4期

刘义艳，郝婷楠，张伟

（1.长安大学能源与电气工程学院，陕西，西安 710018；2.深圳市沃尔核材股份有限公司，广东，深圳 518000）

随着交直流特高压输电技术的发展与电力线路的建设，我国电网正在向大规模交直流互联的方向发展，跨大区的全国互联电网将会日益完善.复杂的电力系统给电网的安全稳定运行带来了极大的挑战[1].若电网长期处于异常运行状态，会危害供电侧和用电侧的输配电安全.如何充分挖掘电力大数据的潜在价值，快速准确地实现故障的自动识别和定位，提供可靠的评估结果，感知和预警电网运行过程中的风险，制定紧急控制措施，减少经济损失，有效保障电网稳定运行，对智能电网的发展具有重要的意义[2-3].

目前对电网监测数据的处理包括时域分析、数据驱动等分析方法，近年来电网监测领域涌出一批新兴方法，如机器学习、深度神经网络、循环神经网络等人工智能方法[4-5].深度学习网络，相较于人工神经网络，深度神经网络模型深度更大，算法更加复杂，精度更高[6-7].卷积神经网络（convolutional neural networks，CNN）是深度学习网络的典型代表，具有强大的信号处理能力，尤其在处理多维数据方面优势突出，广泛应用在如图像处理、计算机视觉和大数据分析等领域[8-11].YUAN 等[12]提出了一种基于卷积神经网络(CNN)和长短期记忆(LSTM)神经网络混合模型的检测方法，可以全面挖掘时空信息.丁津津等[13]集成不同总线上的测量值，搭建图卷积网络框架用于配电网故障定位，通过IEEE123 节点基准系统验证了GCN 模型定位故障的有效性并且在有限数量的实测母线下表现良好.CHEN 等[14]提出应用迁移学习算法改进卷积神经网络的方法进行电网异常区域定位，该方法降低了深度学习算法对样本数量的要求，解决了中小样本情况下深度学习在配电网故障定位时学习效果差的问题.

若采用随机矩阵的特征值进行研究，没有考虑特征向量，会存在不能充分挖掘数据信息、丢失特征向量中包含的有用信息的问题[15].目前，在电力系统领域将随机矩阵理论与人工神经网络或深度学习算法相结合应用在工程案例的研究正在开展.魏文兵等[16]将随机矩阵提取的高维特征值输入到CNN 中，借助神经网络的自主学习能力快速评估电力系统暂态电压性.程瑛颖等[17]对状态监测数据构建的随机矩阵特征值统计量进行聚类分级，根据聚类结果判断电能表的运行状态，通过算例分析验证该方法检测异常状态的有效性和时效性，并发现聚类算法具有较好的鲁棒性，抗干扰能力强.

上述研究在电网异常识别方面取得了一定成果，对于采用数据集内的样本所构建的输入特征集，其合理性是影响神经网络异常定位模型准确性的重要因素.因此，为了快速准确地自动定位电网的异常区域，本文采用随机矩阵理论作为数据挖掘中的特征提取方法，对采集的样本构建输入特征集，通过CNN 对输入层的数据源矩阵进行卷积运算优化，构建一个新的特征矩阵，并通过训练该特征矩阵来建立与扰动位置的映射关系，通过建立的映射关系对新的输入层进行学习实现电网扰动源定位.最后以IEEE39 节点电网模型三相短路故障为例，构建RMTCNN 模型，先对训练样本的原始数据提取特征向量，将特征向量输入CNN 模型进行训练，应用测试集验证模型的定位准确率.

1 随机矩阵理论和卷积神经网络

1.1 随机矩阵理论

RMT 结合统计学理论，从电网监测数据组成的矩阵的稳定性角度判断电网内部的状态，可以避免传统分析方法处理数据时对电网模型的过度依赖问题.RMT 内容十分丰富，本文主要涉及到其中两个定律：Marchenko-Pastur 定律和单环定律，这两种定律均是基于矩阵的经验谱分布（empirical spectral distribution，ESD）函数总结的矩阵特征值分布满足的数学规律[18-19].

1.1.1 Marchenko-Pastur 定律

对于一个M×M维Hermitian 矩阵A，其具有M个实数特征值λA=()，定义其经验谱分布函数为

式中：M为方阵的维度；为矩阵的第i个特征值；I(·)为指示性函数，当括号内条件判断为真时，I(·)的值为1，反之值为0.

矩阵元素独立同分布且满足μ(x)=0, σ2(x)=d分布的非方阵XN×T(N＜T)，其样本协方差矩阵定义为

式中：d为矩阵方差；T为矩阵X的列数；XH为矩阵X的共轭转置矩阵.由Marchenko-Pastur 定律有，样本协方差矩阵S的经验谱分布满足概率密度函数

如图1 所示为一个100×110高维矩阵的特征值分布情况.由图1 可知，正常状态随机矩阵的特征值分布近似满足分布函数的曲线趋势，当矩阵环境被破坏后，矩阵的特征值分布偏离分布函数的曲线.

图1 矩阵的Marchenko-Pastur 分布Fig.1 Marchenko-Pastur distribution of matrix

1.1.2 单环定律

对于每一行元素满足独立同分布且服从μ(x)=0,σ2(x)=d分布的非方阵XN×T(N＜T)，其XN×T的奇异值等价矩阵为

式中U为与矩阵同维度的哈尔酉矩阵.定义其矩阵积为

式中L为奇异值等价矩阵个数.对矩阵通过变换得到奇异值等价矩阵之后可将矩阵的特征值映射到复平面，即矩阵有N个复数特征值，提取这些复数特征值的（实部，虚部）数对，单环定律发现所有特征值的数对在坐标平面的分布满足概率密度函数

为了方便计算，在后面的研究分析中，仅考虑L=1的情况.由式（6）有以下结论：高维随机矩阵的奇异值等价矩阵的复数特征值主要分布在内环半径为和外环半径为1 的圆环内，内环半径与矩阵的维度比有关.

如图2 所示为一个100×110高维矩阵的圆环分布情况.结合式（6），可以计算得到内环半径为0.3，外环半径始终为1，由图2 可以看出，正常状态矩阵的特征值大致分布在内外环之间，当矩阵环境被破坏，不满足随机矩阵的条件时，矩阵的特征值全部分布在内环里.

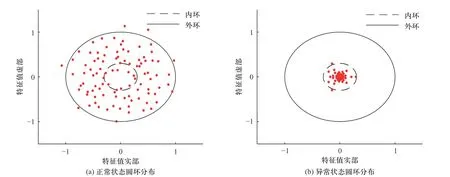
图2 正常状态与异常状态矩阵的圆环分布Fig.2 Ring distribution of normal state and abnormal state matrix

由图1 和图2 可知，从特征值的分布情况可以判断当前矩阵内元素是否满足随机分布，从而判断当前系统内部是否正常，实现实时异常检测.

1.2 卷积神经网络结构

CNN 模型由输入层、隐藏层和输出层三部分组成，结构示意图如图3 所示[20].输入层为输入网络的原始信号或者经过预处理之后的数据；隐藏层是网络的核心，也是区别其他神经网络的部分，卷积神经网络的隐藏层由卷积层、激活层、池化层和全连接层组成，对输入层的数据进行降维和特征提取处理；输出层本质上是一个分类器，对隐藏层输出的特征值进行概率计算，将原始数据划入指定类别，用于分类.

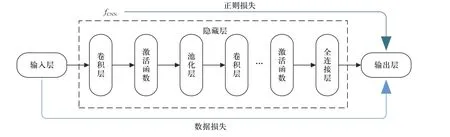
图3 CNN 结构示意图Fig.3 Schematic diagram of CNN structure

①卷积层.

卷积层是卷积神经网络模型的核心部分，贯穿整个网络模型的数据运算处理，卷积层由若干卷积核组成，每一个卷积核均对输入层数据进行有规律的局部扫描，并与扫描到的局部数据进行卷积运算，每一次的卷积结果作为相应位置的特征值，全局扫描完形成若干个通道卷积输出矩阵，并作为下一层网络的输入.

②池化层.

池化层是卷积层之后进一步特征压缩与提取的操作，其主要是通过将卷积输出矩阵中的特征值按一定的函数规律进行聚合，然后再将此规律得到的特征值组合在一起形成一个新的特征矩阵，池化操作可以降低卷积输出矩阵的尺寸，并进一步提取矩阵的特征，提高运算效率的同时防止过拟合干扰，增强模型学习效果.池化过程与卷积运算过程相类似，只是使用的运算函数不一样，二者都是通过建立运算窗口对输入矩阵进行局部扫描运算，保存运算结果作为局部特征，通过将窗口滑动实现全局的特征提取.

③激活函数.

激活函数应用在每一层的输出之前的神经元中，用于对运算结果进行非线性映射，提高网络的表达能力.选择合适的激活函数、神经元数量，调整合适的函数权值，神经网络就可以实现任何一个输入向量到输出向量之间映射函数的逼近，增强特征的特性，便于网络学习与最后的分类.

④全连接层.

全连接层位于隐藏层的最后，作为隐藏层与输出层的衔接层，是卷积运算的最后一步，全连接层将之前所提取到的特征进行最后综合降维，形成一个一维向量特征，便于输出层的分类计算.

⑤SoftMax 分类器.

SoftMax 分类器一般嵌入在输出层里，通过训练集自带的标签对分类器进行训练，形成一定的统计规律，对测试集的全连接层输出的特征值对应每一类标签的概率进行计算统计，概率最大值对应的类别即为分类结果，从而对目标值实现预测或者分类.

⑥目标函数.

卷积神经网络中的目标函数主要用于模型的训练阶段，通过应用函数求取当前模型的输出结果与标签的差值，差值大小用来衡量模型的拟合效果，故目标函数又称为损失函数，损失值越小表明网络预测的效果越好，目标函数值还用于模型的优化，对模型内的神经元权值进行修改，直至损失值达到设定阈值，完成模型优化.根据函数针对的对象类型不同，目标函数可以分为均方误差函数和交叉熵函数两种，均方误差函数针对的是当前输出与标签的误差，交叉熵函数针对的是对输出结果进行分类时，样本对应每个类别的统计概率的分布情况，表达式分别如式(7)和式(8)所示.

式中：M为总的种类数量；yi为当前数据的标签，即目标值，如果目标类别为i，则yi=1，否则为0；为当前模型对输入样本的输出值，即预测值；pi为模型的SoftMax 分类器对当前样本输出进行分类时对应每一类的概率值.根据函数对象的区别可以得知，均方误差函数适用于线性回归、预测等问题时，交叉熵函数适用于分类识别问题.本文的RMT-CNN 网络模型中使用交叉熵函数作为损失函数，用于模型的参数迭代优化.

2 基于RMT-CNN 的异常定位方法

2.1 RMT-CNN 定位模型

本文提出的RMT-CNN 模型结构由RMT 提取特征集和CNN 训练特征集两个部分组成，模型结构如图4 所示，RMT 为数据预处理过程，用于提取监测数据的特征向量作为CNN 模型的输入量，CNN 模型由若干个卷积层、池化层和全连接层组成，通过对RMT提取的特征集进行学习，优化选择最优层数和超参数组合得到最佳CNN 结构，形成样本输入与输出的映射关系，用于无标签样本的故障定位.

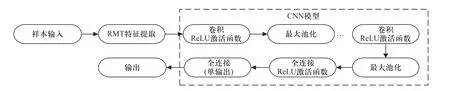
图4 RMT-CNN 模型结构Fig.4 Structure of the RMT-CNN model

2.2 RMT-CNN 定位方案流程

将电网监测信号作为模型的输入，经过随机矩阵理论提取监测信号的特征集后输入CNN 模型，通过CNN 模型将带标签的输入信号的特征与标签形成映射关系，通过映射关系对无标签样本进行分类找到样本对应的扰动位置实现定位.定位的流程如图5 所示.

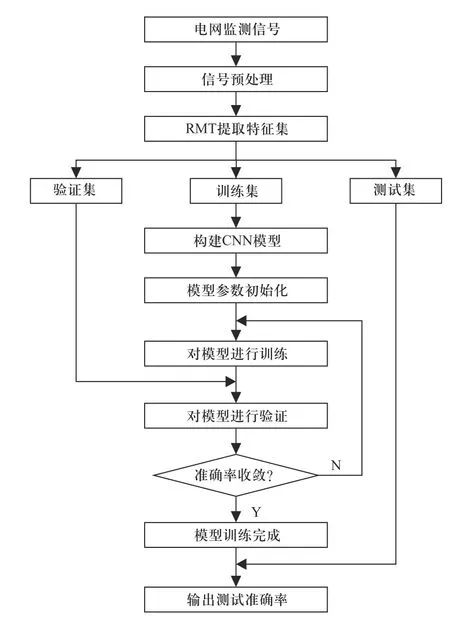
图5 RMT-CNN 定位流程Fig.5 RMT-CNN locating process

具体步骤如下：

①对电网进行区域划分，将一个互联的大电网划分为若干个小区域网络；

②利用每个区域内的监测点同步向量量测装置（phasor measurement unit, PMU）[21]采集的数据分区构造矩阵，将数据集进行归一化处理；

③将样本划分训练集、验证集和测试集，分别用于模型的参数优化、优化结果检验和定位准确率测试；

④将数据集分别作为RMT 块的输入，采用随机矩阵理论的特征向量提取法提取各样本的特征，作为CNN 模型的输入；

⑤设置模型的初始参数，通过训练集对网络进行训练，将验证集代入预训练的模型中计算损失函数和定位准确率，根据结果对模型进行调整，最终获得RMT-CNN 电网故障定位模型；

⑥采用测试集对RMT-CNN 电网故障定位模型进行测试，得到测试结果.

3 数据集预处理

3.1 数据集描述

以IEEE39 节点系统为研究对象，采用PMU 装置测量到的18 个节点72 个电气信号作为原始数据源.对每个节点进行三相短路故障设置，采样频率为1 000 Hz，滑动窗口维度为72×100，即每0.1 s 的监测数据构成一个状态监测矩阵，窗口滑动步长为10，每过0.01 s 构建一个矩阵，将按时间序列选取0.1 s 内构造的10 个矩阵作为一个样本，按此方法在每个节点故障发生后5 s 内随机生成200 个样本，每个样本设置标签1～39 用于表示故障位置，样本总量为7 800 个，将这7 800 个样本按2∶1∶1 划分为训练集、验证集和测试集，用于模型参数训练、检验模型优化程度和检验模型定位准确率.

3.2 RMT 提取特征集

系统内有18 个监测点，每个监测点采集4 个电气量，状态矩阵维度为72×100，设定连续10 个窗口的状态监测矩阵为一个样本数据源，对每个窗口矩阵求取最大特征值对应的72×1大小的特征向量.构造特征矩阵时有两种方法：一种是直接构造法，通过滑动窗口采样，以100 个时间序列矩阵的特征向量构成一个72×100的样本特征矩阵；另一种是分区构造法，将电网分成3 个区域，每个区有6 个监测点，划分情况如图6 所示.因此每个区域矩阵得到的24×1的特征向量组成一个72×1的特征矩阵，同样通过滑动窗口采样，以连续100 个时间序列矩阵的特征向量构成一个72×100的同样大小样本特征矩阵.两种特征矩阵构造方法用同一数据源，构造出两个相同大小的特征矩阵.应用RMT 构造特征矩阵过程如图7 所示.

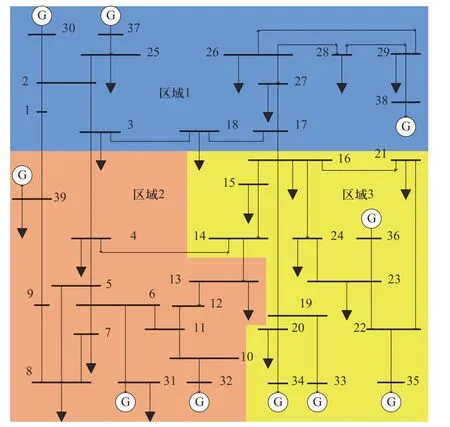
图6 IEEE39 节点电网分区示意图Fig.6 Schematic diagram of node power grid partition about IEEE39

图7 样本特征矩阵构造示意图Fig.7 Schematic diagram of sample feature matrix construction

本文主要采用分区构造样本特征矩阵的方法，图8 为按该方法构造的特征向量.此处仅列出母线1～3 短路时通过随机矩阵理论提取的最大特征值对应的特征向量，每个特征向量长度为72.由图8 可以发现，当IEEE39 标准系统内不同节点发生短路故障时，提取到的特征向量幅值变化趋势不同，因此监测数据组成的高维矩阵最大特征值对应的特征向量元素异常情况能反映不同位置的故障.

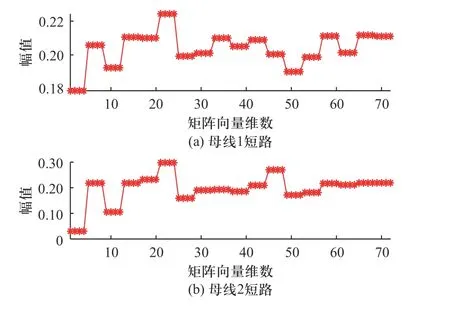
图8 分区构造的特征向量Fig.8 Feature vectors of partition construction

4 算例分析

4.1 超参数设计实验

神经网络模型中的参数对模型的性能影响较大，本节对CNN 模型各参数组合模型进行对比实验分析，寻找最优模型组合参数，提高模型定位识别的效率和准确率.

本文采用准确率A（Accuracy）、精确率P（Precision）、召回率R（Recall）以及F1值作为模型的评价指标.准确率是指识别正确的物体个数与识别物体总数的百分率比值，比值越大准确率越高；精确率表示正确预测为正的样本为正的比例；召回率是指被正确分类样本栈该类样本的比例；F1是综合考虑精准率和召回率的值，反应整体指标.计算公式如下

式中：nTP为真阳性，表示实际类别为正类，预测类别为正类的数量；nTN为真阴性，表示实际类别为负类，预测类别为负类的数量；nFP为假阳性，表示实际类别为负类，预测类别为正类的数量；nFN为假阴性，表示实际类别为负类，预测类别为正类的数量.本文中将故障情况设为负类，正常情况设为正类.

关于神经网络中池化层的池化方式，目前卷积神经网络中池化方式有两种：最大池化和平均池化，最大池化采用最大值函数作为池化函数，均值池化采用平均数函数作为池化函数，通过池化窗口选取原矩阵的局部数据，利用函数运算取该区域的元素最大值作为该区域的池化结果，滑动窗口重复运算.

最大池化法的优势在于池化操作过程中对于数据的纹理特征信息更加敏感，尤其是数据突变时提取的特征更接近原始数据，可以保留特征图中的最大局部特征.本文的电网监测信号比较平稳，当出现异常时信号出现波动或突变，因此采用最大池化方法处理数据可以更加快速准确的发现数据的异常情况.

神经网络的激活函数常见的有三种，如图9 所示.

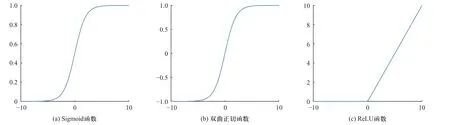
图9 激活函数Fig.9 Active function

Sigmoid 函数和双曲正切函数（tanh）函数为单调递增有界函数，函数如图9（a）、（b）所示，函数上各点处处连续且存在导数，并且通过Sigmoid 函数将神经元的输出值范围控制在0～1 内，相当于进行了一次归一化处理.但Sigmoid 函数的缺陷在于并不一定关于原点对称，趋于无穷大或无穷小时函数曲线趋于平滑，容易造成梯度消失，由于Sigmoid 函数值和导数值均大于0，导致网络反向传递过程各层参数梯度同符号，易使收敛速度下降，无法完成深层网络的训练.

Tanh 函数图形与Sigmoid 函数一样，区别在于输出范围改变为（-1, 1），可以视为Sigmoid 函数的变形结果.这两种函数都属于饱和激活函数，均存在梯度消失问题的缺陷，但Tanh 函数值关于原点对称，收敛速度快于Sigmoid 函数.

为了解决上述两种激活函数梯度消失的问题，提出一种新的激活函数-修正线性单元（rectified linear unit，ReLU），ReLU 函数如图9（c）所示，本文将使用ReLU 作为模型的激活函数.

本节研究卷积网络层数分别为2、3、4 以及卷积层内卷积核不同尺寸、不同数量的组合对准确率的影响.一般神经网络参数调节采用经验法，参数的组合具有一定随机性，无法穷举所有参数组合的模型，因此本文给出多次参数调整后接近最优准确率的组合实验结果.所有模型组合的池化层均采用2×2大小的最大值池化窗口对卷积层输出进行池化处理，池化步长为2，即每次降采样之后维度将会减半，遇到奇数维度时在池化前进行补0 填充后再池化.

由于输入样本尺寸较小，网络深度需求不太高，因此对2 层、3 层、4 层卷积结构的CNN 模型进行卷积核个数与尺寸参数进行设置后，各模型对训练集进行训练学习，完成后使用验证集检验各模型定位故障的准确率，检验结果如图10 的柱状图所示.

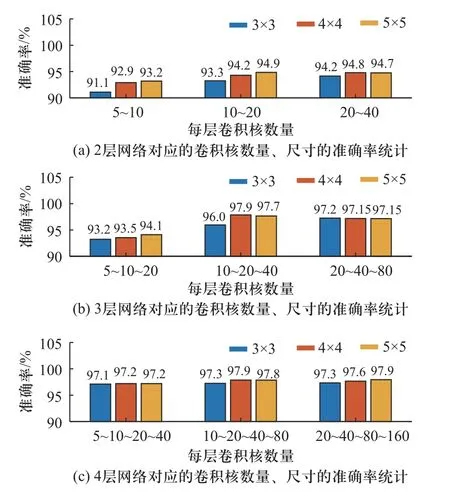
图10 CNN 超参数设计实验结果Fig.10 Experimental results of CNN super-parameter design

由图10（a）可以发现，2 层网络中有2 个卷积层，固定每一层卷积层的核数量不变，每层的卷积核尺寸越大，对接收到的信号的感受域越广，获得的全局特征越好，识别率也会越高.若固定卷积核的尺寸不变，增加每一层的卷积核数量，卷积核数量越多，提取到的局部特征越多，识别率也会提高.观察图10（b）3 层卷积网络的参数组合的定位准确率统计结果可以发现，相较于2 层网络来说，3 层网络增加了模型的深度，模型的训练学习能力更强，定位准确率有了显著的提升，与2 层模型相同的是每层卷积核的个数越多，网络的识别效果越好，但当卷积核数量足够多的时候固定每层卷积核数量增大卷积核尺寸对网络性能的提升效果并不明显，反而带来高计算量.观察图10（c），4 层卷积网络的模型定位率比较稳定，识别效果受模型内卷积核个数和尺寸的大小影响较小.

综合分析图10 中的36 种组合模型的统计结果发现，卷积深度和卷积核的数量以及尺寸都可以在一定程度上增加准确率，但是过度追求网络深度和数量会增加网络训练难度和训练时长.综合以上方案的定位准确率和耗时，最终确定CNN 网络为3 层网络，每层卷积核的数量分别为10、20、40，每层卷积核的尺寸均为5×5.

4.2 模型定位功能分析

通过4.1 节对CNN 网络参数的实验结果对比分析，最终确定搭建的RMT-CNN 的模型结构及其对应的参数如表1 所示.

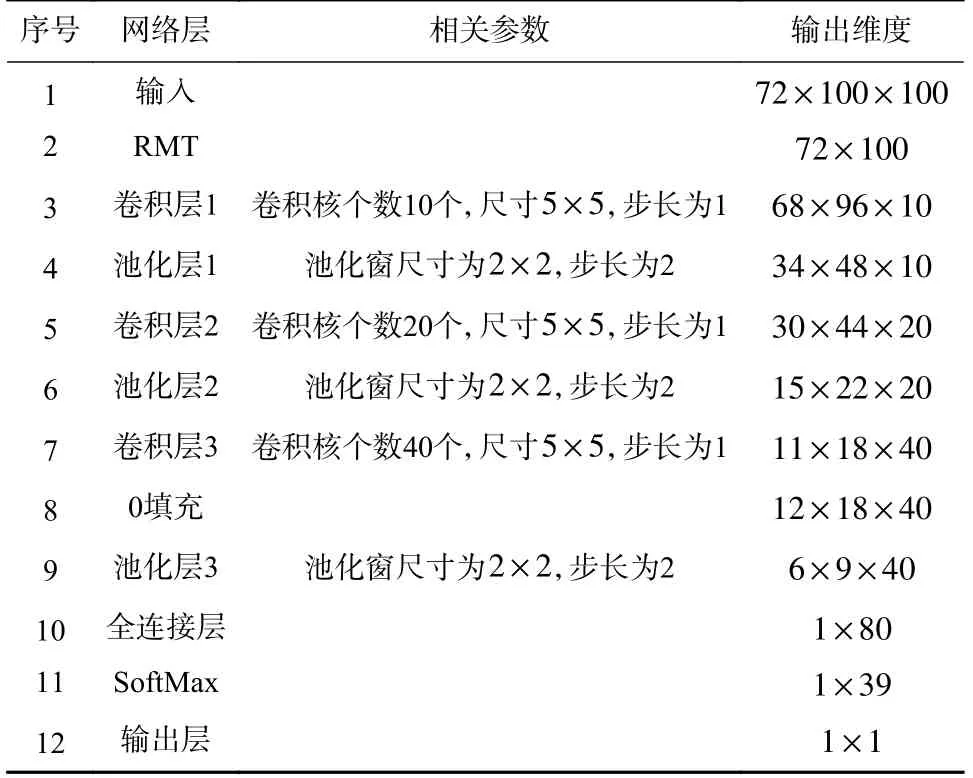
表1 RMT-CNN 电网故障定位模型结构Tab.1 Structure of the fault locating model based on RMTCNN for power grid

确定网络模型后将测试集降本输入上述RMTCNN 模型中，进行定位识别，对识别结果与标签进行对比，统计每个节点的故障定位准确率结果如表2所示.

表2 各节点故障定位准确率Tab.2 Location precision of fault in every node

经统计，39 个节点的1 950 个测试样本的总体定位准确率为97.96%，结果表明该CNN 模型对样本经随机矩阵理论提取的特征矩阵具有较好的分类效果.

4.3 算法性能对比实验

为了验证本文所提方法的优越性，对算法的性能进行了消融实验，通过消融实验，RMT 和分区均可提高CNN 模型的定位准确率.实验结果如表3所示.

表3 消融实验结果Tab.3 Melt experiment results

从表3 可以看出，对于同一个CNN 模型，经过RMT 处理过原始数据后输入CNN 模型的定位准确率均在95%以上，精确率分区RMT-CNN 要比未分区高3%，召回率分区RMT-CNN 要比未分区高2%.比直接应用CNN 模型的准确率有了较大的提升，更利于神经网络的学习与分类；对比两种RMT 提取特征矩阵的方法，提取的特征矩阵均能较好地表征故障数据的特征，其中通过电网分区之后的矩阵提取的最大特征值对应的特征向量对不同故障位置信息更敏感，定位效果更好.