水中旋转圆盘振动阻尼测量与模拟

姚志峰，刘宝熙，曾永顺，白绵绵，王福军

（1.中国农业大学 水利与土木工程学院，北京 100083；2.清华大学 能源与动力工程系，北京 100084；3.陕西省水利电力勘测设计研究院，陕西，西安 710001；4.北京市供水管网系统安全与节能工程技术研究中心，北京 100083）

抽水蓄能作为储能的关键技术对构建新型电力系统、实现双碳目标意义重大，具有广阔的发展前景[1].水泵水轮机作为抽水蓄能的核心装备，为了实现电网对风能和太阳能等新能源的消纳以及满足电网对调峰调频的需求，经常在不同工况间来回切换.在此过程中，水泵水轮机必然经历不稳定运行区，在不稳定区的剧烈的振动是影响机组安全稳定运行的主要因素.而水力阻尼作为水泵水轮机设计中的关键参数，对减小振动、预估流场环境中叶轮动力学特性及其疲劳寿命具有重要意义.

传统的叶轮水力阻尼测量方法需要在静止状态下使用力锤进行激励，通过加速度传感器获取响应信号，再通过对响应信号的处理来获取模态参数.例如，RODRIGUEZR 等[2]和PRESAS 等[3]就将静止叶轮悬挂在水箱中，通过敲击获取叶轮的振动响应.随着材料技术的发展，可控的激励技术和高精度的振动传感器逐渐替代了传统的锤击和加速度计，这为阻尼的准确测量提供了基础支撑.例如，COUTU等[4]在测量水力阻尼的过程中通过压电纤维贴片（piezoelectric macrofiber composites，MFC）激励水翼，并通过激光多普勒测速仪（laser Doppler vibrometry，LDV）测量振动信号.同时，BERGAN 等[5]也通过MFC和LDV 测量了单个水翼在不同流速下的水力阻尼.此外，BERGAN 等[6]通过简化混流式水轮机叶轮为叶栅，在测量阻尼的过程中也利用MFC 产生激励信号.YAO 等[7]在测量水翼水力阻尼时通过锆钛酸铅压电贴片（piezoelectric ceramic material patches, PZT）来激励水翼，通过LDV 来测量振动响应信号.曾永顺等[8]和ZENG 等[9]在测量水翼水力阻尼时利用压电片的正、逆压电效应，直接通过一对PZT 来激励和测量振动信号.

虽然利用新材料新技术后，阻尼的测量精度有所提高并且测量更加便捷，但是以上的研究没有考虑旋转带来的影响.对于水泵水轮机这类水力机械，在实际运行过程中都伴随着旋转，而现有的研究发现在旋转条件下结构的模态特性会发生显著的变化.例如，PRESAS 等[10]通过布置在旋转圆盘上的PZT和加速度传感器获得了旋转下的频率特性，结果表明相同节径下的模态频率呈现前行波频率增加，后行波频率减小的变化.CAO 等[11]通过对灯泡式水力机组转子的研究也发现转子的固有频率随着转速的增加，前行波频率增加后行波频率下降的变化.CHEN 等[12]对水中螺旋桨进行了不同转速下的振动测量，得到螺旋桨的水力阻尼随着转速的增大而逐渐增大的规律.但CHEN 等在实验时实际上是将加速度传感器放置在螺旋桨连接轴的轴承上，并没有直接测量水中旋转叶片的水力阻尼特性.旋转中的水力机械进行振动测量时，在高压和高剪切应力的旋转流动中，存在激励和响应获取困难的问题.而实际中的水泵水轮机叶轮体形较大且结构复杂，现有的激励测量设备需要输入较大能量，并且在旋转环境中，传感器的安装牢固性也难以保证.

与实验手段相比，数值模拟方法获取阻尼是一种高效且经济的途径.目前，基于计算流体动力学（computational fluid dynamics，CFD）和计算结构动力学（computational structure dynamics，CSD）的双向流固耦合法是获取水力阻尼的常用数值模拟方法.例如，LIAGHAT 等[13]通过双向流固耦合法计算了水翼在不同流速下的水力阻尼比.同样，ZENG 等[14]通过双向流固耦合研究了不同来流下的水翼水力阻尼值.但是，为了保证计算精度和收敛性，双向流固耦合方法需要设置较小的时间步长，这个过程需要消耗大量的计算资源.目前在水翼等简单结构上该方法的使用较为普遍，针对叶轮等复杂结构，该方法的使用还不常见.MONETTE 等[15]发展了一种基于模态做功测量水力阻尼的新方法，也称为模态做功法或者能量法，模态做功法基于振动过程中的能量产生和耗散平衡假设，利用模态计算得到的振型和频率耦合CFD 中动网格技术实现对振动能量的计算.模态做功法相比于双向流固耦合法极大地缩短了计算时间.MONETTE 等基于该方法计算了不同流速下水翼的阻尼，通过和实验以及双向流固耦合法的结果做对比，验证了该方法在水翼等结构上的可靠性.TENGS 等[16]通过模态做功法也对水翼在不同流速下的阻尼进行计算，通过和实验结果对比也验证了该方法的可靠性.WANG 等[17]也利用模态做功法对水翼的水力阻尼进行了计算,但是这些研究没有考虑旋转条件下带来的影响.针对旋转下的水力机械，GAUTHIER 等[18]基于模态做功法得到混流式水轮机零节径模态在设计工况下的水力阻尼约为0.15，在部分载荷工况下的水力阻尼略低.ZHANG 等[19]和MING 等[20]运用模态做功法获得了轴流式水轮机的水力阻尼以及在考虑叶片间相互影响的情况下的水力阻尼.虽然考虑了旋转的因素，但是这些结果没有实验结果的支撑，而最初的模态做功法基于简单水翼问题而提出，对于旋转条件下的适用性和准确性问题研究还很少.

目前，大部分研究者在研究叶轮振动特性的过程中都将其简化为圆盘[10,21-22]，该简化具有诸多优点.本研究同样利用圆盘代替叶轮，基于PZT 激励并获取振动信号，设计了在旋转效应作用下圆盘的水力阻尼测量系统，获取了圆盘阻尼随转速的变化规律，通过与实验结果对比，评估了模态做功方法在旋转条件下获取阻尼的适用性和准确性.

1 旋转圆盘振动阻尼测量系统

1.1 阻尼测量装置

阻尼测量系统的原理如图1 所示.基于PZT 的压电效应（当外界压力施加于PZT 时，PZT 产生电压，当给PZT 施加电压时，PZT 产生机械变形），通过信号发生器生成可控信号，经过压电放大器后传递到PZT，进而将激励传递给圆盘.在PZT 激励下，其他PZT 获取响应信号，并通过采集卡传递给计算机处理.圆盘转速通过无级变速器控制，转速工作范围为0～2 000 r/min.通过滑环完成旋转圆盘和静止测量部件之间的信号传递，进而实现水力阻尼的定量测量.

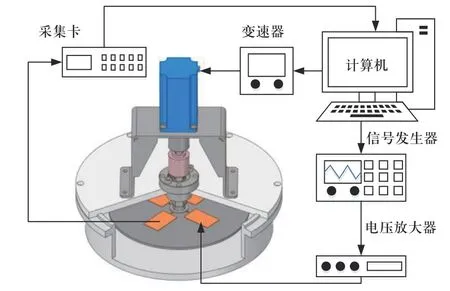
图1 阻尼测量系统原理Fig.1 Principle of damping measuring system

具体装置如图2 所示，其中电机固定在支座上，通过联轴器带动轴旋转，滑环固定在旋转轴上.轴通过传动端和非传动端轴承分别固定在水箱的盖板和底座上，并带动圆盘旋转.圆盘厚度为3.12 mm，直径为300 mm，材料为铝合金，密度为2 700 kg/m3.将4 个PZT 和连接线嵌入圆盘中跟随旋转，并进行激励和响应获取.考虑到圆盘尺寸较大，为获取清晰的振动响应信号，采用额定电压更大的P-876.A12 型PZT.该PZT 工作电压范围-100 ～400 V，长、宽和厚度分别为61 mm、35 mm 和0.5 mm，相互之间成90°夹角布置，如图3 所示.配套使用的压电放大器型号为E-413.D2，额定放大倍数为50.选用滑环为DT2045中空式电滑环，内径为20 mm.

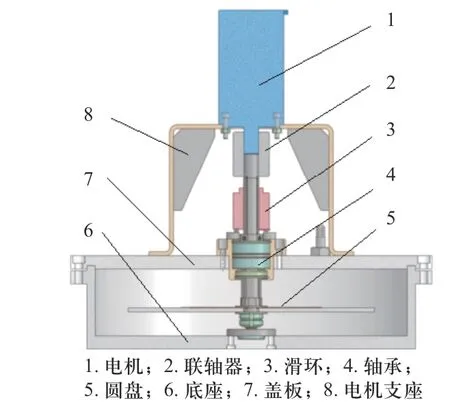
图2 实验台示意图Fig.2 Schematic diagram of the test bench

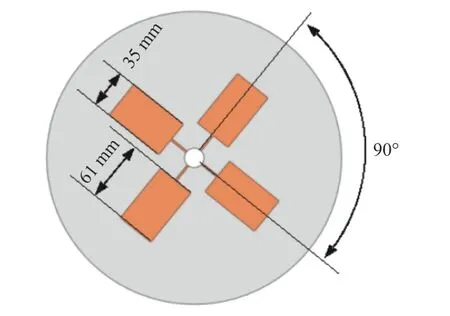
图3 PZT 布置Fig.3 PZT arrangement

1.2 阻尼测量方法

通过变速电机驱动圆盘旋转后，在稳定转速下旋转一定时间，再通过信号发生器输入扫频信号.压电片对结构施加的扫频激励信号可表示为

式中：F(t)为外载荷，N；F0为激励幅值，m； ωe为扫频激励角频率，rad/s.

当扫频频率接近圆盘固有频率时，圆盘发生较大振动，通过PZT 可测得较为明显的响应信号，利用快速傅里叶变化即可识别对应的固有频率.对于周期性激励的强迫振动阻尼识别采用共振放大法，运动方程的动力放大因子可表示为[23]

在已知扫频频率 ωe和固有频率 ωn情况下，通过函数拟合式(2)，可得到对应的阻尼比 ζ.

1.3 系统可靠性验证

对于本研究的阻尼测量系统，在圆柱坐标系中圆盘的运动可以由图4 表示，即圆盘进口边rin处受到固定约束，此处的轴向位移为0，出口边rout处不固定约束，圆盘绕着轴做旋转运动.

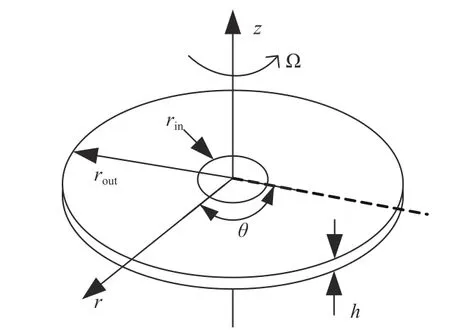
图4 圆盘旋转运动示意图Fig.4 Motion diagram of disk rotation

圆盘在极坐标系下的自由振动方程可以表示为[24 - 25]

式中： ρs为圆盘密度，kg/m3；h为圆盘厚度，m；w为轴向位移，m；r为圆盘某一点到旋转轴的距离，rin≤r≤rout，m；D为刚度，N/m； θ为周向角度，0＜θ ＜ 2π，rad；E为杨氏模量，Pa； υ为泊松比.

圆盘轴向位移的解为[10]

式中：n为节径数量；m为节圆数量；ωnm为节径节圆对应的固有频率，rad/s；Wnm(r)为径向相关的位移.

将式(5)代入式(3)中可得：

式中λnm是与圆盘进出口半径以及振型相关的系数.

当不考虑节圆的影响时，式(5)和(6)可以分别简化为[24-25]：

式中：An(r)为位移函数；r0=为平均半径，m；D*为等效刚度，可根据实验率定.

在转速为0 的情况下，根据2 节径模态实验结果率定D*值，对于2～8 节径的结果如表1 所示，实验和理论结果的偏差在7.9%以内.

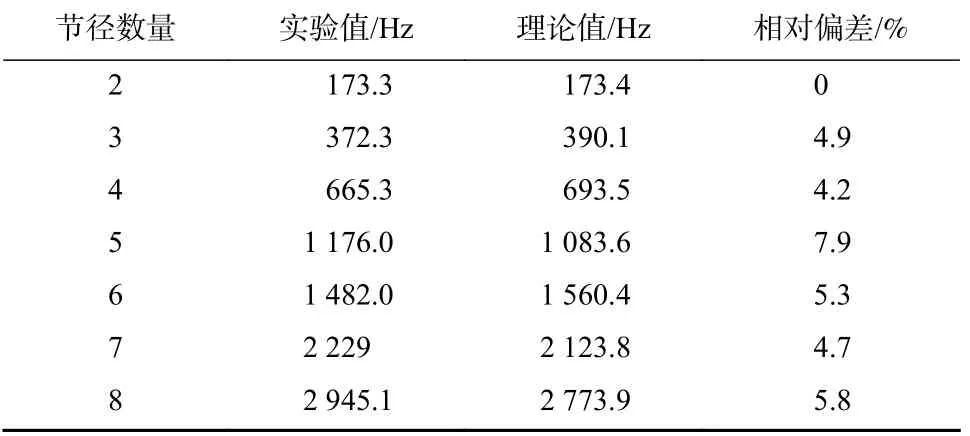
表1 空气中圆盘固有频率Tab.1 Disk natural frequencies in the air

2 水力阻尼数值模拟方法

2.1 水中模态理论

对于水中圆盘模态，将Navier-Stokes 方程简化为声波方程[26-27]

式中ua为水中声速，m/s.

离散式(9)，耦合结构动力学方程后得到有限元离散方程[26-28]

式中：Ms为结构的质量矩阵；Cs为结构的阻尼矩阵；Ks为结构的刚度矩阵；Mf为水体的附加质量矩阵；Cf为水体附加的阻尼矩阵；Kf为水体附加的刚度矩阵；Mfs和Kfs分别为耦合系统的质量和刚度矩阵；下标f 和s分别表示流场和结构场.

2.2 阻尼计算理论

当圆盘在水中旋转振动时，与水体相互作用会导致振动能量耗散，关于振动系统的能量耗散，可通过结构承受的阻尼力乘以振动速度并对时间积分计算得到[15]

式中：ΔW为一个振动周期内的能量耗散，J；f(d)为阻尼力，N.

假设结构以固有频率做简谐运动，则运动方程可表示为

式中y0为结构简谐运动的幅值，m.

耦合式(11)～(13)，可得：

结合方程：

可得：

式(17)中，未知参数包括模态质量M、固有频率ωn、振动幅值y0及ΔW，对于水中结构：

在计算水力阻尼时，首先基于模态分析方法，求解结构在水中固有频率ωns.同时，将振型的幅值正则化处理后，可计算得到空气中模态质量[29]

式中Es为振动系统的总动能，J.

之后，基于模态分析方法，求解结构在水中的振型和中固有频率 ωnf，并根据空气中和水中固有频率计算水体附加质量

对于水力机械而言，结构刚度Ks远大于水体附加刚度Kf.例如，对于一台轴流式水轮机，Kf/Ks＜2%[18]，此时可忽略水体附加刚度的影响，式(21)可简化为

最后，将水中振型导入流场中进行非定常计算，并根据固有频率进行周期性振动.此时，式(17)中的y0为振型的幅值.在非定常CFD 中，计算预设模态在一个振动周期内的能量损失，可表示为

式中：N为振动周期，s；为振动结构承受的面法向压力，Pa；为剪切应力，Pa；S为流固耦合交界面的面积，m2.

3 数值计算设置

数值计算基于商业软件ANSYS17.1，模态计算采用Modal 模块，水力阻尼计算采用CFX 模块.

3.1 模态计算

圆盘模态计算模型包括圆盘本身、旋转轴以及周围的水体.支撑约束位于旋转轴上，通过设置不同转速，带动圆盘旋转.同时，周围水体设置密度为1 000 kg/m3，声波速度为1 486 m/s.在圆盘及旋转轴与水体的交界面处设置流固耦合交界面，模态计算网格划分如图5 所示.

图5 模态求解设置Fig.5 Modal solution settings

3.2 流场非定常计算

提取圆盘周围的水体作为流场的计算域，采用结构化网格对计算域进行划分，对圆形区域采用O型切分，并对靠近圆盘以及旋转轴表面的网格进行加密处理以提高计算的精度，如图6 所示.总网格数为221 万，在10 Hz 转速下，圆盘表面y+在1 以内，其他壁面y+在30 以内.

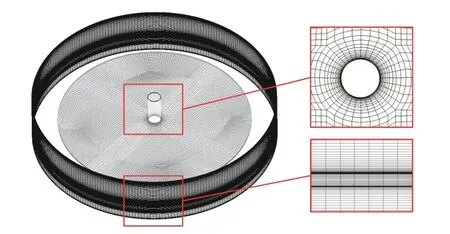
图6 流体域网格划分Fig.6 Fluid domain meshing

在流场计算中，除圆盘与周围水体的交界面设置为运动壁面，其他面均为固定壁面，且所有壁面满足无滑移条件.利用模态计算得到的振型以及固有频率，将圆盘振型导入到CFX 中，如图7 所示.圆盘与水体的交界面设置为周期性位移，运动周期设置为对应振型的固有频率，同时围绕轴做旋转运动，旋转方向和速度与实验值保持一致.为了保证计算出的结果有较高的精度，以对应转速的定常计算结果作为初始值，将时间步长设置为较小的5×10-6s，每一个时间步内最大迭代20 次，残差收敛准则为1×10-6.同时，对圆盘与水体交界面的功率密度做积分，并输出随时间变化的结果.当输出的功率密度在每个振动周期内变化基本一致时，提取多个振动周期内的功率密度值并对时间做积分，之后除以周期数，取平均值作为该工况下的振动周期内能量的耗散值.

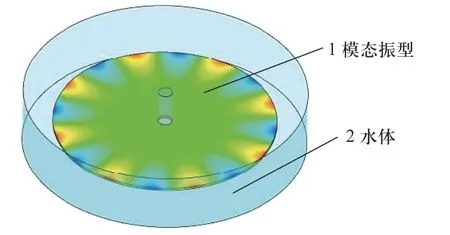
图7 CFD 计算设置Fig.7 CFD calculation settings

4 结果与讨论

4.1 圆盘振型

对于圆盘振型常用“（节径数量，节圆数量）”表示，由于对称结构拥有两个频率接近且同节径的振型，在旋转过程中会出现频率升高和下降的现象，分别用“forward”和“backward”来区分.模拟得到的振型如图8 所示，蓝色代表振动幅值较小或为0，红色代表振动幅值较大，黑色线框表示未发生变形的圆盘边缘.可以看到随着节径（蓝色条纹带）的增加，圆盘周向的起伏程度越来越明显.

图8 典型节径振型Fig.8 Typical nodal diameter mode shape

根据PZT 获取信号的原理，PZT 形变程度越剧烈，得到的信号越明显.本研究考虑到信号获取的精度以及模拟计算时间长度的问题，选择对（8，0）振型进行分析.如图9 所示，可以看出，最大振动位移发生在圆盘外缘，并呈现高低起伏的现象，这和式(5)描述的运动规律一致，即当r固定时，θ变化时会导致轴向位移周期性起伏.

图9 圆盘振型Fig.9 Disc mode shape

4.2 圆盘频率

在静水中，圆盘扫频激励下的响应如图10 所示，当扫频激励频率接近或者等于圆盘本身的固有频率时，圆盘发生较大振动，经过PZT 可获取到较大的响应信号.通过对该信号进行FFT 变换后如图11 所示，可以看到较为明显的峰值，其中峰值对应了相应振型的固有频率.而在旋转条件下，圆盘的扫频结果如图12 所示，在旋转下，噪声信号明显增多，并且在30～35 s 之间可以看到两个较为接近振动响应信号，通过FFT 变化后如图13 所示，可以看到两个明显的峰值.

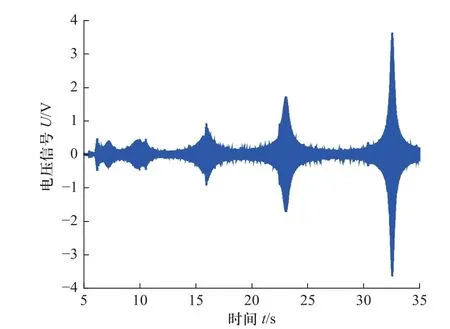
图10 静止圆盘扫频时域Fig.10 Stationary disk time domain

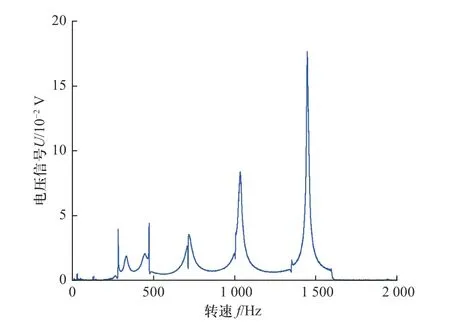
图11 静止圆盘扫频频域Fig.11 Stationary disc frequency domain

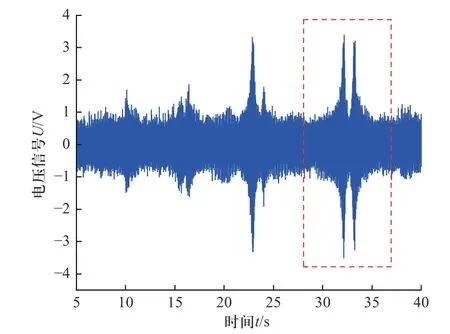
图12 旋转圆盘扫频时域Fig.12 Rotation disk time domain

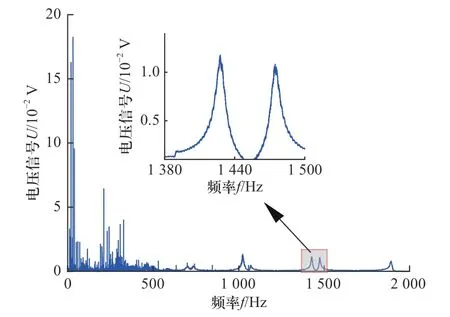
图13 旋转圆盘扫频频域Fig.13 Rotation disk frequency domain

通过重复性实验后，最终结果取算术平均值，圆盘在水中不同转速下的（8，0）固有频率如图14 所示，由于圆盘属于对称结构，在静止条件下相同节径振型的固有频率较为接近，随着转速的增加，（8，0）forward 频率也随之增加，而（8，0）backward 频率随着转速增加而减少，该结果与多数研究者得到的结果一致.

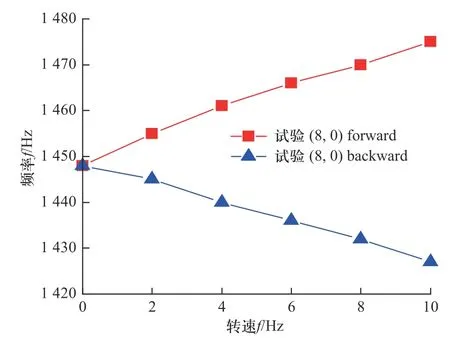
图14 固有频率随转速的变化Fig.14 The natural frequency varies with rotational speed

4.3 圆盘阻尼

对于实验测量的阻尼比，如图15 所示，当扫频频率接近1 462 Hz 时响应达到最大，利用式（2）拟合就可得到对应的阻尼比.对于模拟结果，旋转下的振动圆盘不断地与水体发生能量交换，当圆盘在稳定振动时，说明外界激励的能量和圆盘耗散的能量达到平衡，通过计算耦合界面的能量耗散特性就可求得水力阻尼.振动圆盘的壁面能量耗散特性如图16所示，可以看到（8，0）模态的能量耗散呈现正弦形式，能量耗散的过程存在一定的微小波动，但总体随时间正弦变化趋势没有改变.

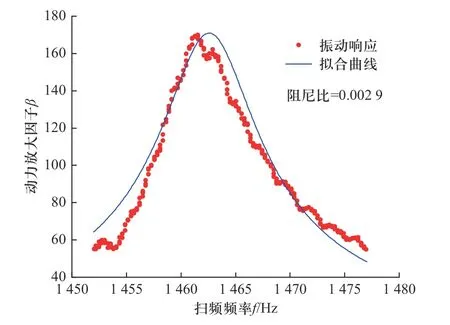
图15 阻尼计算方法Fig.15 Damping calculation method

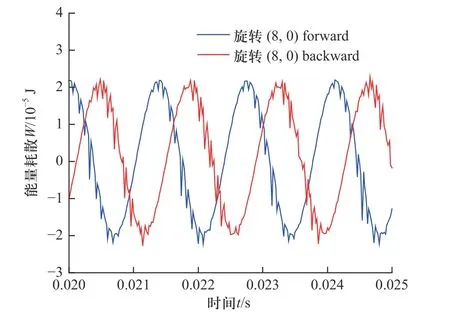
图16 CFD 能量耗散特性Fig.16 CFD energy dissipation characteristics

通过实验和模拟计算，不同转速下（8，0）振型对应阻尼比如图17 所示，实验表明，随着转速的升高，阻尼比呈现下降趋势.对于实际中高转速运行的水力机械，需要注意随着转速的上升，水力阻尼比可能减小进而诱发剧烈振动.当振动幅值较大时，可能导致静止部件与旋转部件的摩擦和碰撞，严重危害机组的安全稳定运行.

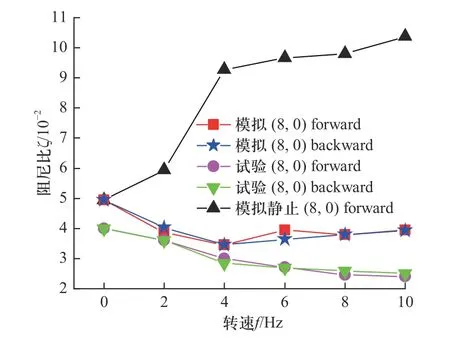
图17 圆盘阻尼结果对比Fig.17 Comparison of disc damping results

对于模拟结果，在不考虑旋转时，由于静止条件下（8，0）forward 和（8，0）backward 固有频率接近，振型基本一致，尽管有相位差异但是振动周期内两者做的功基本相等，故本研究只计算了（8，0）forward 随转速变化的阻尼值.可以看到，随着转速的增加阻尼比也增加.如果直接使用静止条件下的振型和频率，水力阻尼比的预测趋势完全和实验相反.在考虑旋转的条件下，可以看出，在4 Hz 转速前，阻尼比随着转速下降，当超过该转速后，阻尼比有上升趋势，但是变化不大.模拟结果和实验结果存在一定的偏差，在10 Hz 时，偏差为64.5%.考虑旋转效应后水力阻尼的预测精度在10 Hz 转速下相比不考虑旋转有所提高，并且预测趋势也有所改进，基本符合实验规律.但是，在4 Hz 转速后模拟和实验值的偏差逐渐增大.偏差增大的原因可能是在转速逐渐上升的过程中，由于液体黏性，圆盘边界与液体产生较大剪切力，数值计算对剪切力引起的阻尼变化考虑不足.因此导致了转速越高与实验的偏差越大.

这说明使用模态做功法计算旋转结构的水力阻尼时，必须考虑旋转效应带来的影响.总的来说，模态做功法计算阻尼中具有较大应用前景，该方法相比实验测量和双向流固耦合计算具较大优势，但是该方法的精度还有待提高，需要后期进一步的研究.

根据PRESAS 等[10]的研究，由于离心力和科式力的作用，旋转不仅改变了圆盘的固有频率而且改变了圆盘的振型.显然，在旋转过程中，离旋转轴越近的位置受到的轴向约束越强，而离旋转轴越远的位置在径向受到的离心越大，旋转除了带来振型和频率的变化还会改变流体的流动特性，但旋转对水力阻尼的影响机理目前还没有清楚的定论.在旋转条件下，各种因素的耦合更加明显，对于实际中的水泵等设备而言，在运行时存在导叶和叶轮之间的动静干涉、叶片的漩涡脱落、淹没深度变化以及空化等因素的影响[30].并且，随着复合材料的推广应用，结构动力响应更难预测[31].这些因素都会使得水力阻尼的预测研究会变得困难，其变化机理需要更深入的研究.本研究的内容可为旋转式水力机械设计过程中水力阻尼评估和利用模态做功法计算水力阻尼提供参考和借鉴.

5 结 论

水力阻尼的准确预测对水力机械的研发具有重要意义.本研究利用旋转圆盘阻尼测量系统，获取了不同转速下的水力阻尼值，通过对比模态做功法获得的水力阻尼，对模态做功法的精度和适用性进行了评估.主要结论为：①随着转速的增加，圆盘的水力阻尼值呈现下降趋势，对于实际中高速运转的水力机械需要注意旋转效应可能带来的水力阻尼下降问题；②模态做功法在计算水力阻尼时必须考虑旋转效应带来的影响，如果直接使用静止条件下的模态参数，则阻尼的变化趋势完全和实验结果相反，并且结果产生较大偏差；③模态做功法在考虑旋转后，预测值随转速变化的整体趋势与实验一致，但呈现过预测的问题，最大偏差为64.5%，该方法的影响因素和预测精度还需要进一步深入研究.