面向多核向量加速器的卷积神经网络推理和训练向量化方法*

陈 杰,李 程,刘 仲

(国防科技大学计算机学院,湖南 长沙 410073)

1 引言

近年来,以卷积神经网络为代表的深度学习技术不仅在图像识别[1-3]、自然语言处理[4,5]等领域发挥了巨大的作用,而且在金融[6,7]、推荐算法[8,9]和物理学[10]等领域也同样彰显了重大的应用价值。然而,卷积神经网络模型的性能提升是以庞大的数据和计算量为前提的。传统CPU(Central Processing Unit)设计的侧重点在于通用性,集成了较多的控制单元,对深度学习的加速效果不够理想。为了加快深度学习计算,许多科技公司投入了大量人力物力,用于定制深度学习加速器,如谷歌的张量处理器TPU(Tensor Processing Unit)[11]、海思研发的NPU(Neural network Processing Unit)[12]和英特尔研发的深度学习训练加速器NNP(Nervana Neural network Processors)[13]。这些深度学习加速器具有更高的并行处理能力,在面向深度学习领域应用时的功耗和效率表现要远强于通用CPU的。

FT-M7004是一款由国防科技大学自主研发的多核向量加速器,在大规模矩阵乘法、快速傅里叶变换等科学计算应用领域能够实现较高的计算效率。FT-M7004采用了单指令流多数据流SIMD(Single Instruction Multiple Data)技术和超长指令字VLIW(Very Long Instruction Word)架构,支持标向量混合运算,具备强大的并行处理能力。卷积神经网络的计算瓶颈主要在于卷积层和全连接层,因为这2层算子的实现需要大量的乘加运算。FT-M7004也集成了大量的乘加器,在加速卷积神经网络的计算上拥有显著优势。然而目前基于多核向量加速器的深度学习推理和训练算法还缺乏系统性的研究。

卷积神经网络主要由数据输入层、卷积层、激活函数、池化层和全连接层组成,其中计算主要集在卷积层和全连接层。文献[14]指出卷积层占据了90%～95%的计算量。因此,如何高效地实现卷积层的推理和训练算法是研究的重点。在算法层次上,Img2col[15,16]、Winograd算法[17,18]、Cook-Toom算法[19]和FFT(Fast Fourier Transform)[20]用于实现卷积层推理,col2img用于实现卷积层训练。Img2col主要是通过将图像数据和卷积核数据展开为二维矩阵的形式,以矩阵乘法的形式实现卷积计算。Img2col算法的缺点是需要在每一层对数据进行转换,存在较多的冗余空间开销。Winograd算法将图像数据和卷积核数据分割成块,并将数据展开,之后将乘法转变成加法。在卷积核尺寸较大时,Winograd算法加速效果不佳。Cook-Toom算法与Winograd算法类似,其加速效果和使用范围均不如前者的。卷积操作同样可以转换成FFT来加速,之后再进行逆变换得到最终结果。当卷积核尺寸较小时,FFT算法加速效果收益不大。同时,由于上述算法主要应用于CPU和GPU,与FT-M7004平台的体系结构差异较大,所以需要针对多核向量加速器设计新的推理和训练算法。

本文针对自主设计的多核向量加速器FT-M7004上的VGG[21]网络模型推理和训练算法,分别提出了卷积、池化和全连接等核心算子的向量化映射方法,并进行了性能测试与分析。本文工作主要包含以下几个方面:

(1)分析了FT-M7004体系结构的特点;

(2)提出了卷积、池化和全连接算子的前向推理和反向训练算法的向量化映射方法;

(3)采用DMA(Direct Memory Access)双缓冲传输、向量并行和权值共享等优化策略,在FT-M7004平台上对上述算法进行优化;

(4)对不同规模的卷积、池化和全连接算法进行了性能测试与分析。

2 FT-M7004的体系结构

FT-M7004包含CPU和向量加速器2种处理器核心。CPU用于运行操作系统,进行任务管理;向量加速器采用VLIW和SIMD体系结构,为FT-M7004提供了主要的计算能力。FT-M7004集成了4个向量加速器核,单核单精度浮点运算峰值性能可以达到128 GFlops。每个加速器的核心由1个标量处理单元SPU(Scalar Processing Unit)和1个向量处理单元VPU(Vector Processing Unit)组成。SPU主要用于标量运算和流控管理,并支持将标量寄存器的数据广播到VPU中的向量寄存器,使得SPU可以为向量单元运算提供数据。VPU集成了16个同构的向量处理单元VPE(Vector Processing Element)。每个VPE包含了4个乘累加MAC(Multiply ACcumulate)单元,提供了大部分的算力。FT-M7004的片上阵列存储器AM(Array Memory)采用了多存储体的组织方式,能同时支持2个向量存储操作和DMA向量数据访问操作,为VPU提供了多达2 048位的访存带宽,能够满足16个VPE的高并行SIMD计算需求。

3 卷积神经网络算法实现

3.1 符号说明

本节将对本文算法中使用到的符号进行说明。所有张量的索引都是从0开始。图像和权重的原始数据分别采用NCHW(N表示图像批处理大小,C表示图像通道数,H表示图像的高度,W表示图像的宽度)和OCHW(O表示卷积核数量,C表示卷积核通道数,H表示卷积核的高度,W表示卷积核的宽度)布局。令N表示批处理的图像数量;F′表示网络每一层前向推理的输入张量;Z′表示网络每一层前向推理的输出张量;dZ′表示网络每一层训练的输入张量;dF′表示网络每一层训练的输出张量;pF′表示对输入张量F′的所有特征图外围填充零后的张量;Zd,i,j表示卷积层输出的第d幅特征图第i行第j列的值。卷积层和池化层输入图像的通道数为C,输出图像的通道数为O,高度和宽度分别为nH和nW。WEI表示卷积核或全连接层的权重,bias表示偏置向量,卷积核的高为kH,宽为kW,卷积步长为st。WEId,c,m,n表示4维卷积核张量WEI在索引[d,c,m,n]处的值。在池化层,池化单元的高、宽和步长的表示与卷积层的一致。全连接层的符号同理。X[m,k]表示矩阵X中第m行、第k列的元素。M[d:]表示矩阵M中第d行的元素,M[d:m,]表示矩阵M中第d行到第m行的元素。矩阵Ar*c,表示A的行数为r、列数为c,bias[n]表示向量bias第n个位置的元素。Zn,d,i,j表示卷积层第n个样本在第d个通道第i行第j列的值。X[:i]代表矩阵X的第i列。全连接层的输入神经元个数为K,输出神经元个数为M。Abs表示一个函数,当输入值为负时,输出值为0,否则仍为输入值。pad表示输入特征图边缘填充零的个数。Max(x,0)表示对输入的标量x与0进行比较,取其中的最大值。

3.2 数据布局

本文算法将卷积神经网络前向计算的输入特征数据和反向传播的输入误差梯度进行存储。如图1所示,每一列存储一个样本数据,每列的存储顺序为:首先为图像通道C方向优先,接着是图像宽度W方向优先,最后是图像高度H方向优先;如图2所示,卷积核张量存储为二维卷积核矩阵,其中矩阵的每一行表示一个卷积核,每行的存储顺序首先为卷积核宽度kW方向优先,接着是卷积核高度kH方向优先,最后是卷积核通道C方向优先。本文算法均采用这种数据布局,因此卷积神经网络中的张量都将转换为二维矩阵。为了便于区分3.1节中的张量,以F和Z分别代表实际的输入和输出张量,WT表示实际的权重。

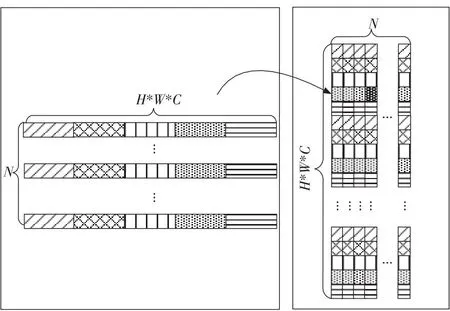
Figure 1 Input image layout conversion

Figure 2 Weight data layout conversion

3.3 卷积层推理算法

直接卷积算法如式(1) 所示,单次只能计算一个输出值,效率较低,且需要对原始输入进行补0,存在较大的数据搬运开销。

pF′t,c,i*st+m,j*st+n)

(1)

本文提出了一种批图像融合卷积计算算法,可以将卷积计算转换成大规模矩阵乘法,如图3所示,同时也不需要对原始图像进行补零填充。

Figure 3 Implementation of convolutional algorithm

如算法1所示,可以提前计算当前卷积区域填充0的个数,只从卷积核矩阵和输入图像矩阵提取实际参与运算的行与列。令卷积区域左上角的元素所在行为i、所在列为j,则其上方填充零的行数up0为Max(pad-i,0),其下方填充零的行数down0为Max(pad+kH-H-pad,0),其左侧填充零的列数left0为Max(pad-j,0),其右侧填充零的列数right0为Max(j+kW-W-pad,0)。实际参与运算的输入图像矩阵的起始行号为i+up0-pad,起始列号为j+left0-pad。实际参与运算的卷积核矩阵的起始行号为up0,起始列号为left0。通过行号和列号即可提取对应的子矩阵。

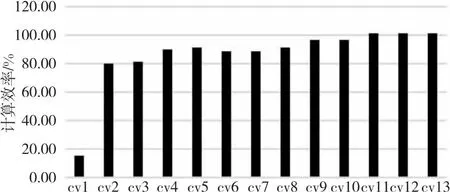
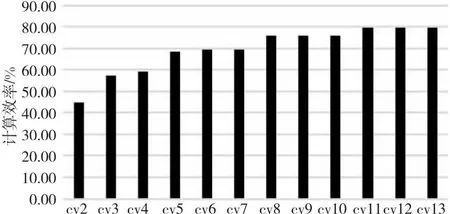
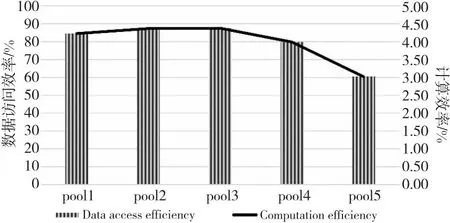
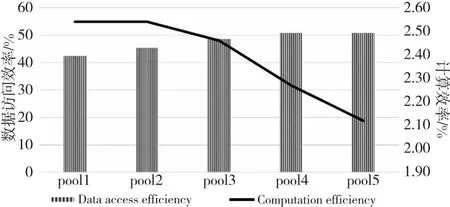
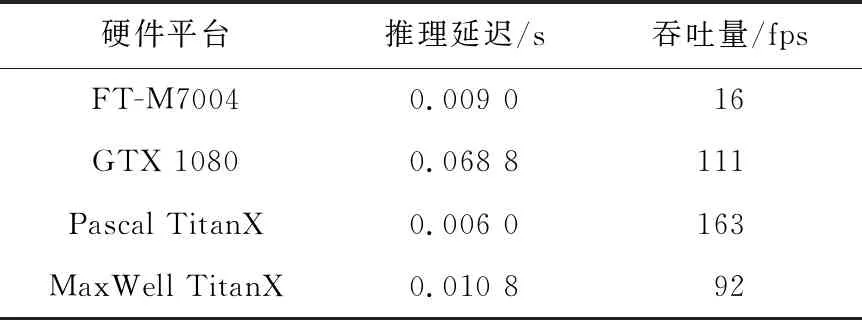
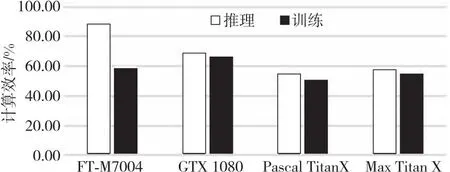
算法1 Conv_forward输入:F,WT。输出:Z。步骤1 pH=H+pad*2,pW=W+2*pad;步骤2 for (int h=0;h

接下来定义被提取的卷积核子矩阵为W,输入图像的子矩阵为M,则有式(2):

(2)

其中,x=d+i*O*nW+j*O。

3.4 卷积层训练算法

从卷积层的推理过程,可以得到卷积层对输入图像的梯度,如式(3)所示:

(3)

其中,i′=i*st+m,j′=j*st+n,i∈[0,nH-1],j∈[0,nW-1]。式(3)可继续化简为式(4):

(4)

其中,m=i′-i*st,n=j′-j*st,且m∈[0,kH-1],n∈[0,kW-1]。当(i′-m)/st∈[0,nH-1]且(i′-m)可被st整除,同时(j′-n)/st∈[0,nH-1]且(j′-n)可被st整除时,式(4)可进一步化简为式(5):

(5)

令δdZl,o,i*st,j*st=dZ′l,o,i,j,且对于δdZ′l,o,k,t,若k不可被st整除或t不可被st整除,则δdZ′l,o,k,t为0。由式(5)可推出式(6):

(6)

其中,i′≥m且j′ ≥n。

令δpdZ′l,o,i+kH-1,j+kW-1=δdZ′l,o,i,j,且对于δpdZ′l,o,k,t,若k∈[0,kH-2]或t∈[0,kW-2] ,则δpdZ′l,o,k,t为0。由式(6)可推出式(7):

(δpdZ′l,o,i′-m+kH-1,j′-n+kW-1×WEIo,c,m,n)

(7)

令m′=kH-1-m,n′=kW-1-n,可得到式(8):

WEIo,c,kH-1-m′,kW-1-n′)

(8)

式(8)可等价转换为式(9):

WEIo,c,kH-1-m,kW-1-n)

(9)

令rotWo,c,m,n=WEIo,c,kH-1-m,kW-1-n,如式(10)所示。卷积核的训练过程实质是在dZ′的每个矩阵行列间直接插入st-1行列零元素后(即δdZ),再在元素外围填充高度和宽度为kH-1和kW-1的零元素后的梯度矩阵(即pδdZ′),作为新的卷积层的输入。旋转180°后的卷积核矩阵rotW作为卷积核。两者进行卷积计算得到的结果。但是,由于填充零的过程中存在大量的数据搬移开销,效率低下。本文提出了算法2,避免了填充零带来的额外开销,同样以矩阵乘法的形式实现了其中的核心计算。

(10)

算法2 Conv_backward输入:dZ,Weight。输出:dF。步骤1 for (int h=pad;h

为了确定rotW矩阵中真正参与运算的行与列,算法2中使用hS来记录卷积核中参与运算的起始行号,使用wS来记录卷积核中参与运算的起始列号。原梯度矩阵的起始行号h0对应pδdZ′中梯度矩阵的第h0*st+kH-1行。原梯度矩阵的起始列号w0对应rotW每个矩阵中的第w0*st+kW-w列。实际参与卷积计算的梯度矩阵每一列的元素间隔st-1个元素,每一行间隔st-1个元素。最后类似算法1中提取子矩阵的方式,在不对原数据填充零的情况下,完成卷积层的训练。

3.5 池化层推理算法

针对FT-M7004的体系结构,本文使用算法3来高效实现最大池化层的计算。

本节使用index矩阵记录Buffer中每一列的最大值,并计算其对应F中的行号,得到输出图像的子矩阵。

3.6 池化层训练算法

以最大池化层为例,对于每一个输出位置Z′n,d,i,j,都需要找到其对应的输入位置F′n,d,i′,j′,并继续传播输入的梯度。具体算法实现如算法4所示。

算法4 MaxPool2d_backward输入:dZ。输出:dF。步骤1 for(int c=0;c

算法4中pos代表推理时最大值所对应的行号,k代表最大值对应的列,算法的核心是将dZ矩阵第row行第k列的值累加至dF中的第pos行第k列。

3.7 全连接层推理算法

全连接层的本质是矩阵乘法,其计算如式(11)和式(12)所示:

(11)

Z=WT×F+bias

(12)

具体计算如算法5所示。

算法5 FC_forward输入:F,WT,Bias。输出:Z。步骤1 for (int i=0;i

每次将矩阵WT第i行第j个元素乘以矩阵F第j行元素,并将结果累加至矩阵Z的第i行,相较朴素矩阵乘法拥有更好的空间局部性。

3.8 全连接层训练算法

从全连接层的推理过程不难得出对权重和偏置求导的式(13)和式(14):

(13)

(14)

dW[i,k]的值即为dZ的第i行与F的第k行相乘,dF[k,j]的值为dZ的第j列与WT的第k列相乘,如式(15)所示:

(15)

然而向量加速器在矩阵间列运算上的效果表现不佳,所以需要对式(15)进行转换,转置矩阵为WT,则有式(16):

(16)

所以,dF就等于转置后的WT矩阵与dZ矩阵进行矩阵乘法。具体算法如算法6所示。

算法6 FC_backward输入:dZ,lr。输出:dF。步骤1 for (int i=0;i

由式(13)可知,bias梯度的每一个值实际上对应了dZ矩阵每一行的和。

4 面向FT-M7004平台的优化

面向FT-M7004平台,卷积神经网络推理和训练算法的优化需要经过以下步骤:首先,需要对数据进行预处理,将图像数据和权重数据的布局进行调整;其次,将输入图像数据从DDR(Double Data Rate synchronous)内存中传输到阵列存储器AM(Array Memory);再次,对核心计算进行向量并行优化;最后,将训练结果从向量空间传输到DDR内存中。在以上步骤中,涉及到的优化有以下几个方面:

(1)数据布局预处理;

(2)DMA双缓冲区传输;

(3)权值共享;

(4)向量并行优化。

4.1 数据布局预处理

在第1层卷积计算过程中,图像数据通过DMA转置传输到向量阵列存储器(AM)中,单个样本的图像数据全部存储在同一列中。第1层卷积计算完成后,图像数据通过DMA传回DDR并保持相同格式。在后续的卷积、池化、全连接等计算过程中,图像数据的存储格式保持不变。这种数据格式有助于将大量小规模的卷积计算直接转化为大规模的矩阵乘法,并以行连续的方式进行数据访问,可以最大限度地实现计算的向量化和并行化,提高计算性能和内存访问效率。

4.2 DMA双缓冲区传输

本文提出DMA 双缓冲区的数据搬移优化策略。首先,在AM中划分一块区域用于存放输入图像数据;其次,将该区域划分为A和B2个缓冲区,在将一个输入图像的子矩阵传入A缓冲区后,开始计算的同时,将下一个输入图像的子矩阵传入B缓冲区;在A缓冲区计算完之后,再将下一个输入子矩阵传入A缓冲区,同时进行B缓冲区的计算。采用这种方式可以实现计算与数据搬移重叠,若数据传输时间小于计算时间,则可以有效隐藏数据传输时间,从而提高整体计算效率。

4.3 权值共享

卷积权重数据通过DMA广播传输到每个核的标量存储器SM(Scalar Memeory)。只需一次DDR数据访问即可实现所有参与计算的图像的权重数据共享,可以大大减少权重数据的传输时间,同时最大程度地实现权重数据的共享。

4.4 向量并行优化

权重数据通过标量Load指令读入第k个标量寄存器(Rk),然后通过广播指令传送到第k个向量寄存器(VRK)。图像数据通过向量Load指令读入第i个向量寄存器(VRi)。VRK和VRi的乘加并行计算是使用SIMD的向量化计算。 向量处理器的并行计算效率可以通过标量和向量之间的协同计算来最大化。

5 实验与结果分析

5.1 实验环境

本文的实验目标平台是FT-M7004,另外选择了NVIDIA®的GTX 1080、Pascal Titan X和Maxwell Titan X进行对比实验。

5.2 正确性分析

本文选取了不同批大小的图像数量作为输入,使用Caffe框架推理和训练VGG16模型的结果作为输出,将两者转换为FT-M7004上的数据布局用于对照。结果如表1所示,可以看到,对于不同的批图像大小,本文的推理和训练算法均能输出正确的结果。

Table 1 Results correctness analysis

5.3 性能分析

5.3.1 卷积层推理性能分析

衡量卷积层算法性能的一个重要指标是计算效率。计算效率可通过实际性能与理论峰值性能的比值来得到。测试结果如图4所示,分别列出了VGG16模型中13种不同的卷积层在推理时的计算效率。随着卷积核个数的增多,计算效率得到了稳步提升。在最后一个卷积层,计算效率甚至可以超过100%,这是因为本文提出的算法不需要额外填充零,理论峰值性能考虑到了填充零带来的影响,所以偏低。

Figure 4 Convolution computation efficiency of VGG16(Inference)

5.3.2 卷积层训练性能分析

卷积层训练性能测试结果如图5所示,分别列出了VGG16模型中12种不同的卷积层在训练时的计算效率。可以看到,随着卷积核个数的增多,计算效率依次增加。

Figure 5 Convolution computation efficiency of VGG16(Training)

5.3.3 池化层推理性能分析

池化层推理性能测试结果如图6所示,分别列出了VGG16模型中5种不同的池化层推理时的计算效率和数据访问效率,其中折线表示计算效率。从图6可以看出,池化层的计算效率很低,平均约为4.00%。这是由于池化层的计算量较小,大部分时间开销集中在数据搬移上。然而,池化层的数据访问效率非常高,平均约为80.00%。这是因为池化层所有数据访问都是根据本文提出的算法以访问矩阵行的形式实现的。

Figure 6 Performance of pooling layer(Inference)

5.3.4 池化层训练性能分析

池化层训练性能测试结果如图7所示,分别列出了VGG16模型中5种不同的池化层训练时的的计算效率和数据访问效率,其中折线表示计算效率。从图7可以看出,池化层在训练时的计算效率很低,平均约为2.39%,数据访问效率平均约为47.59%。造成池化层训练性能不如推理性能的主要原因在于,根据本文提出的训练算法,通过数组记录最大值位置的方式不能实现对矩阵的逐行访问,更多时间花费在了不规则的数据访问上;而池化层的计算量占比极小,对性能影响不大。

Figure 7 Performance of pooling layer(Training)

5.3.5 全连接层性能分析

全连接层性能测试结果如图8和图9所示,分别列出了VGG16模型中3种不同的全连接层在推理和训练时的计算效率。由于全连接层的矩阵较大,最小的权重矩阵尺寸为4096*1000,最大尺寸为25088*4096,所以计算效率极高,推理时计算效率平均达到了93.17%,训练时计算效率平均达到了81.98%。全连接层训练时,本质上也采用了矩阵乘法的形式,所以能达到较高的计算效率。

Figure 8 Computation efficiency of fully connected layer(Inference)

Figure 9 Computation efficiency of fully connected layer(Training)

5.3.6 与GPU平台的性能对比

与GPU平台的性能对比结果如表2和图10所示。表2是FT-M7004与其他3款高性能GPU在VGG16模型上的推理延迟(单位为s)和吞吐量(单位为fps)测试结果。在推理延迟方面,每推理一幅图像,GTX 1080的用时为0.068 8 s,Pascal TitanX的为0.006 0 s,MaxWell TitanX的为0.010 8 s,而FT-M7004的为0.090 0 s。吞吐量方面,GTX 1080每秒钟可推理111幅图像,Pascal TitanX每秒可推理163幅图像,MaxWell TitanX每秒可推理92幅图像,而FT-M7004则每秒可推理16幅图像。产生这一性能差距的原因在于3款高性能GPU的峰值性能远高于FT-M7004的,GTX 1080的峰值性能为9 TFlops,Pascal TitanX的为11 TFlops,MaxWell TitanX的为6.7 TFlops,而拥有4个加速器核心的FT-M7004的峰值性能为512 GFlops。图10分别列出了4种硬件在VGG16模型上的计算效率。在推理时,FT-M7004的计算效率能达到87.76%,效果最为出色。在训练时,FT-M7004的计算效率为59.74%,仅次于GTX 1080的65.52%。这是因为GTX 1080的浮点运算能力峰值和带宽比FT-M7004平台的高,训练时需要的计算量和访存量更大。

Table 2 Analysis of inference delay and throughput表2 推理延迟与吞吐量分析

Figure 10 Performance comparison of different platforms

6 结束语

面向FT-M7004平台,本文完成了对卷积算子、池化算子和全连接算子的优化。本文结合 FT-M7004平台的特性,使用向量并行化、DMA双缓冲传输和向量并行优化等优化方法,提高了程序 的性能。实验结果表明,在 FT-M7004平台上,本文提出的算法能够较好地考虑到体系结构的特点,实现极高的计算效率。同时,本文还与NVIDIA GPU平台进行了实验对比,推理时计算效率领先20%以上,训练时计算效率虽然不是最佳,但性能差距不大。后续将针对其他深度学习算子完善其在FT-M7004平台上的实现与优化。