无线携能通信下mmWave协作通信小单元的能效最优策略*

卢明妤,李陶深,吕 品

(1.广西大学计算机与电子信息学院,广西 南宁 530004;2.南宁学院信息工程学院,广西 南宁 530200;3.广西医科大学基础医学院,广西 南宁 530021)

1 引言

第五代移动通信技术5G(the 5th Generation mobile communication technology)的到来使得具有高计算性能的智能终端设备和数据流量呈爆炸式增长,这给传统的能量受限的无线网络带来了新的挑战。5G的关键性能要求除了基于用户侧千倍提高的用户体验速率和毫秒级时延等需求之外,在频谱效率SE(Spectral Efficiency)和能量效率EE(Energy Efficiency)方面将较传统无线网络有大幅度的提升。这些需求的提升给5G技术的应用带来了极大挑战。一是通信网络存在严重的干扰和能源消耗;二是由于超密集小区的部署,回传网络的规划变得越发困难。为了应对急剧增长的能源消耗问题,能量收集EH(Energy Harvesting)技术是一种通过收集的射频RF(Radio Frequency)信号为能量受限的无线通信网络提供绿色可持续的能量,从而使系统生命周期得到延长的有效手段[1,2]。由于RF信号既是信息的载体,也是能量的载体,在此基础上将无线能量传输WPT(Wireless Power Transfer)和无线信息传输WIT(Wireless Information Transmission)集成的无线携能通信SWIPT(Simultaneous Wireless Information and Power Transfer)因其自身的优势而倍受关注。因此,为了满足5G无线网络中高频谱效率与低能耗的绿色通信需求,将能量收集技术中的SWIPT技术应用于设备到设备D2D(Device-to-Device)通信和毫米波(mmWave)协作通信中,并研究分析该系统性能极具科学意义[3]。

在mmWave频段下可以获得大量频谱资源,从而可以获得更高的数据速率,但由于高频具有高路径损耗和对障碍物敏感等特点,因此mmWave不适合远距离传播。但是,超密集小区的部署能大大减少WPT的传播损耗,因此,WPT可能更适合在5G网络框架下实施。文献[4]关注5G新频率下的SWIPT网络设计和优化,设计了一个双频SWIPT网络,其中高频频段用于短距离信息传输,而低频频段用于短距离能量传输和长距离信息传输。文献[5]构建了一个由Sub-6GHz和mmWave小单元基站组成的无线供能的蜂窝网络,评估了该网络中收集的能量和吞吐量,说明了在密集的场景中,mmWave能比Sub-6GHz获得更高的吞吐量。文献[5,6]分别将Sub-6GHz和mm Wave 2个频段的WIT和WPT的性能进行比较,结果表明mmWave在能量收集和网络吞吐量方面比Sub-6GHz有更好的效果。文献[7]研究了无线能量传输与mmWave通信在无线传感器网络中的技术结合,提出了几个不同复杂度的位置感知扇区选择方案。文献[8]研究了SWIPT在mmWave大规模多输入多输出MIMO(Multiple-Input Multiple-Output)和非正交多址接入NOMA(Non-Orthgonal Multiple Access)系统中的集成,将问题分解为高维模拟预编码和低维数字预编码,通过联合优化mmWave大规模MIMO-NOMA的功率分配和SWIPT的功率分流因子,实现速率的最大化。目前,采用mmWave进行WPT和WIT的研究已取得一定进展,但研究成果仍十分有限。

SE和EE作为衡量系统性能的关键指标,在传输性能和能耗之间做出权衡并实现高能效无线通信成为了设计未来无线通信模式的首要考虑因素。文献[9,10]的研究表明,可以通过采用NOMA等方法来提高SE。一些学者从资源分配算法层面对EE进行优化,在满足用户服务质量要求的同时,最大化利用有限的网络资源。为了在保证宏小区服务质量的前提下实现小小区能量效率的最大化,文献[11]提出了一种联合功率带宽分配方案,并设计了一种快速收敛的2层迭代算法来获得所提分配方案的最优解。考虑同信道干扰和跨层干扰,文献[12]为非正交多址异构蜂窝网HCN(Heterogeneous Cellular Network)提出了一种次优算法来交替优化宏小区和小小区的子信道和功率资源分配,以实现整个系统的EE最大化。文献[13]在保证蜂窝用户服务质量和D2D链路的EH约束的情况下,提出了基于Dinkelbach和Lagrange的联合EH时隙分配、功率和频谱分配迭代算法。文献[14]通过将子信道分配和功率控制解耦,设计了一种低复杂度的子信道匹配算法,使用拉格朗日对偶的功率优化算法来最大限度地提高能量效率。文献[15]利用最大最小概率机和Dinkelbach方法,将NP难问题转换为较易求解的凸优化形式,提出了一种分布式对偶资源分配算法。文献[16]基于凸优化方法提出了一种迭代最优功率分配和功率分流PS(Power Splitting)算法,并通过仿真实验验证了算法的有效性。文献[17]利用定向波束成形技术实现mmWave的高速回程,通过并发传输调度和功率控制将能耗最小化,提出一种高效节能的mmWave回程方案,并证明了该方案在能量效率方面具有优越性。文献[18]研究在mmWave小单元中实现D2D通信的节能多播调度问题,提出了一种高效节能的组播调度方案,通过调整链路的传输功率降低能耗,并确保吞吐量。

在现有的采用mmWave技术进行能量收集的研究中,大多仅考虑了基于发射端的无线供能通信网络WPCN(Wireless Powered Communication Network)的情况,即考虑从射频信号能量源中,如基站、接入点AP(Access Point)、能量信标PB(Power Beacon)收集毫米波能量,用于后续的信息传输,并没有考虑基于接收端的SWIPT的情况,但在D2D通信中发射端和接收端是一个完成配对的设备对,不应该分开考虑。为此,本文针对5G通信网络高频谱效率与低能耗的绿色通信需求,考虑将mmWave应用到传统的D2D接收端的SWIPT之中,一种基于SWIPT下mmWave协作通信小单元的能效最优策略,即在最小链路传输速率和最小收集能量的联合约束下,通过优化发射功率控制和功率分流因子,最大化系统链路能量效率,以解决WPCN模式下系统能量收集阶段的下行SWIPT阶段的能量受限型用户设备UE(User Equipment)链路的能效优化问题。

2 系统模型

2.1 mmWave协作通信小单元网络模型

由于严重的路径损耗以及对阻塞敏感等特点,采用mmWave进行远程访问蜂窝网络是比较困难的,但却给短程通信提供了巨大机会,可见在未来很长一段时间之内部署的是高低频混合组网的蜂窝小区。与此同时,现有的部分研究论证了采用PB为蜂窝用户提供上行传输能量及mmWave进行UE之间信息交换的可行性。为此,本文考虑在5G场景下的一个高低频混合组网的蜂窝网络小区(如图1所示),在宏基站BS(Base Station)覆盖的范围之内,有多个适合采用mmWave技术传输的mmWave小单元,例如高速热点网络、车联网或小蜂窝等。其中,BS工作在Sub-6GHz频谱范围,为其他的mmWave小单元提供额外的信号服务UE。在网络模型中,PB周期地为小单元内的所有UE供能,以确保整个小单元能维持正常运行,而信息的传输与交换则通过mmWave只发生在UE之间。由于采用mmWave通信,mmWave小单元与宏小区工作在不同的频带之上,因此宏小区和mmWave小单元之间的干扰是可以避免的。因为mmWave具有定向传输、路径损耗率高等特点,所以对于mmWave小单元之间的干扰及室内外mmWave小单元间的干扰几乎可以忽略不计。

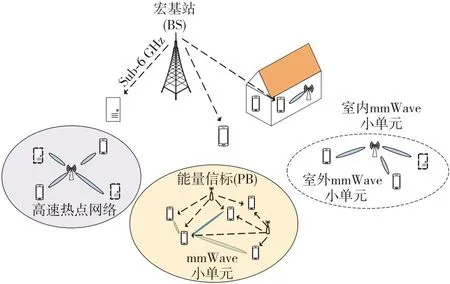
Figure 1 5G high-low frequency hybrid networking cellular cell

为了更好地描述UE之间的无线能量与信息联合传输,本文将UE分为发射机TX(Transmitters)和接收机RX(Receivers)。在目的接收机请求阶段,RX向小单元内其他UE发送所需的相应信息内容的请求信号;收到请求信号的UE在搜索自身信息后,若其自身存在RX所需的信息内容则被标记为备选源发射机。在选择最佳源发射机阶段,带有所需信息内容的备选源发射机均采用mmWave波束向RX发送信号。当TX向RX发送mmWave信号时,由于该mmWave波束既是信息的载体也是能量的载体,因而考虑采用PS实现SWIPT的方式,将RX上接收到的波束信号分成能量流和信息流2部分,分别用于能量收集和信息解码,从而实现能量和信息同时传输。

2.2 mmWave信道模型

除了具有高路径损耗的特性之外,mmWave还存在对阻塞敏感的特点,即如果一个或多个建筑物阻塞与正在进行mmWave通信的设备之间的直接链路相交,那么会产生较高的衍射和穿透损耗。为此,本文的mmWave信道模型采用文献[19]提出的三态阻塞模型:(1)若不阻塞则链路状态为视距状态LOS(Line-Of-Sight);(2)若存在阻塞现象则链路状态为非视距状态NLOS(Non Line-Of-Sight);(3)若链路太弱,则称为中断状态(OUT)。

在上述3种链路状态下,mmWave信道经历不同的信道条件,对于其信道衰落,当链路处于LOS状态时,采用Nakagami-m衰落,服从伽马分布;当链路处于NLOS状态时,服从瑞利衰落分布。相应地,对于路径损耗,本文采用如式(1)所示分段函数表示:

(1)

其中,r(T,R)表示从TX到RX的链路长度,slink表示链路状态,αL表示链路在LOS状态下的路径损耗因子,αN表示链路在NLOS状态下的路径损耗因子,2≤αL≤αN,并假设当链路处于OUT状态时路径损耗为无穷大。

2.3 TX-RX配对后的系统模型

在能量和信息联合传输阶段,本文考虑的mmWave小单元系统模型如图2所示。

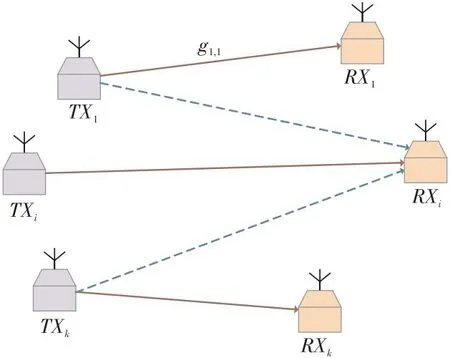
Figure 2 UE paired system model in mmWave small cell

图2包含K对能量受限的发射机(TX)和接收机(RX),分别用集合ФTX={1,2,…,K}和ФRX={1,2,…,K}表示。出于计算能力和资源节约方面考虑,假设所有的能量受限设备均配备单一天线。假设每个RX均采用SWIPT技术,从对应的TX发射的mmWave信号中,使用功率分流的方法从所能接收到的信号中收集一定水平的能量[17]。则第i个RX上接收到的信号可以表示为:

(2)

假设每个RX采用功率分流方式将所收到的信号分成2股功率流,功率分流结构如图3所示,则在RXi处的信息解码功率流表示如式(3)所示:

(3)

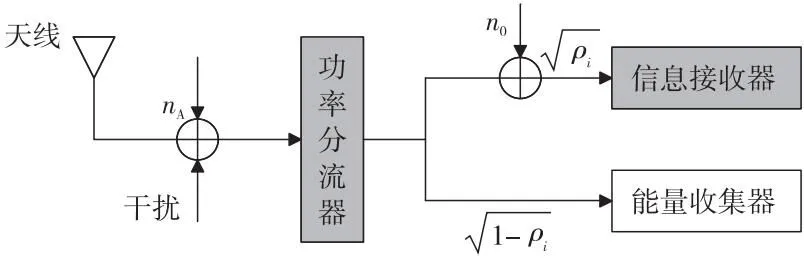
Figure 3 RX structure of power splitter

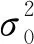
RXi处的信噪比为:

(4)

其中,Pi表示TXi的发射功率,对应的Pj表示其他共信道干扰的TX的发射功率。

根据香农公式,第i对UE的单位带宽吞吐量可表示为:

Ri=lb(1+SINRi)=

(5)

同理,用于能量收集的功率流的表达式如式(6)所示:

(6)

由于噪声nA和n0携带的能量太小,不能激活能量收集电路从而被收集利用,因此忽略噪声后,在RXi处所能收集到的能量线性正比于接收总功率和能量转化效率η(0<η<1),可以表示为:

(7)

根据线性功耗模型[18],第i对UE的总功耗为:

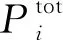
(8)

其中,ξ∈[1,∞)表示功率放大器效率,Pcir表示滤波器、数模转换器等模块的静态电路消耗功率[5]。

定义第i对UE上的能量效率为:

(9)

3 问题描述与最优值求解

为了实现绿色通信的目标,本文将在最小速率和最小能量收集的联合约束下,通过发射功率控制和功率分流因子的优化,尽可能使单位功率传输更多比特,因此将所有UE的能量效率作为优化目标,则优化问题P的数学模型表示如式(10)所示:

s.t.C1:Ei≥Emin,∀i∈Φ

C2:Pi≤Pmax,∀i∈Φ

C3:0<ρi<1,∀i∈Φ

C4:Ri≥Rth,∀i∈Φ

(10)

其中,Emin,Pmax和Rth分别表示RX上的最低能量收集限制、TX上的最大允许发射功率以及UE链路上的最小速率阈值,Φ={1,2,…,K}表示UE对的集合索引。

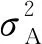
s.t.C1:(1-ρi)η(Pigi,i+Ij,i)≥Emin,

∀i∈Φ

C2:Pi≤Pmax,∀i∈Φ

C3:0<ρi<1,∀i∈Φ

(11)

由于优化问题P的目标函数是一个非凸的分式规划问题,约束条件较复杂,因此使得该问题具有NP难性质。为了求解这个优化问题,可以使用Dinkelbach方法[21],将该非凸的分式规划问题转化为等价的凸形式的减式问题。Dinkelbach方法等价转化过程可以描述如下:

(12)

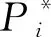
其次,利用以下引理求出能效的最优解:

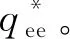
(13)

由文献[21]知引理1成立。

运用Dinkelbach方法,可得到等价的减法形式的目标函数。因此,原优化问题P可重写为:

s.t.C1:(1-ρi)η(Pigi,i+Ij,i)≥Emin,∀i∈Φ

C2:Pi≤Pmax,∀i∈Φ

C3:0<ρi<1,∀i∈Φ

(14)

重写后的问题P是一个凸优化问题,可以采用常见的凸优化方法(如拉格朗日对偶方法)进行求解。式(14)的拉格朗日函数为:

L(Pi,ρi,λ1,i,λ2,i,λ3,i,λ4,i)=

(15)

其中,λ1,i≥0,λ2,i≥0,λ3,i≥0,λ4,i≥0分别表示C1～C4的拉格朗日乘子,拉格朗日函数(15)的对偶函数为:

(16)

由KKT(Karush-Kuhn-Tucker)条件[22]可求得:

(17)

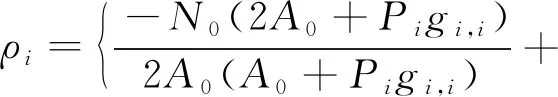
(18)

其中,A0=Ij,i+NA,{x}+=max{0,x}。拉格朗日乘子λ1,i,λ2,i,λ3,i,λ4,i可以采用梯度下降法迭代更新,如式(19)～式(22)所示:

λ′1,i=[λ1,i-α((1-ρi)η(Pigi,i+Ij,i)-Emin)]+,

∀i∈Φ

(19)

(20)

(21)

(22)

其中,α是保证收敛的步长。

采用上述拉格朗日对偶法求解凸优化问题,并通过梯度下降法迭代更新拉格朗日乘子,可知本文提出的在最小链路传输速率和最小收集能量的约束下,联合优化发射功率和功率分流因子,从而最大化系统链路能量效率的策略,可以通过交叉迭代的算法来求解。因此,本文提出一种交叉迭代的算法来求解优化问题P,具体描述如算法1所示。

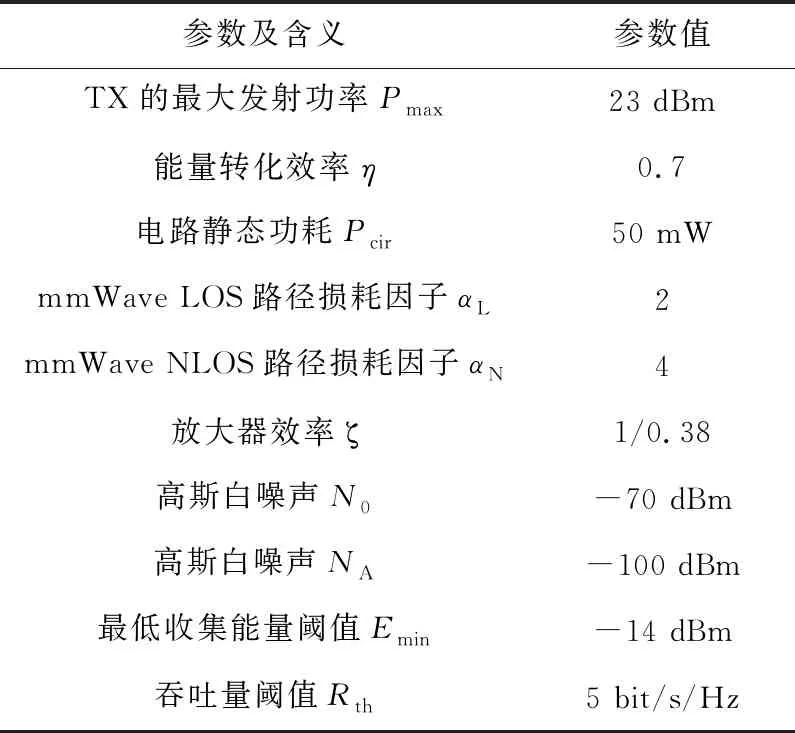
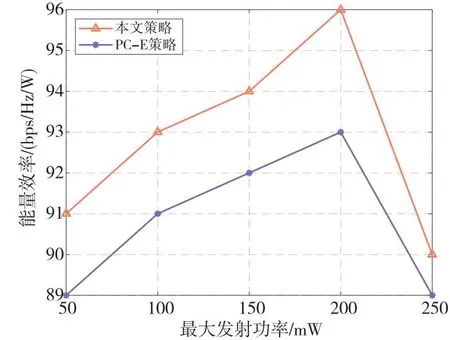
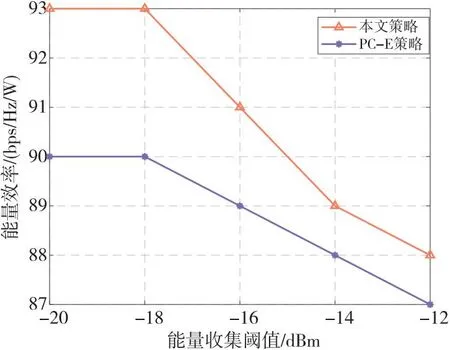
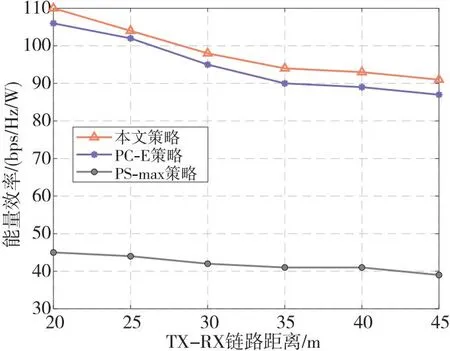
算法1 发射功率控制和功率分流因子的交叉迭代算法输入:能量转化效率η,路径损耗因子αL和αN,高斯白噪声N0和NA,电路静态功耗Pcir,放大器效率ξ,阈值Emin、Pmax和Rth,最大迭代次数T,收敛阈值ε,迭代步长α。输出:最优P*i,ρ*i和q*ee。1)初始化Pi,ρi和qee,拉格朗日乘子λ1,i、λ2,i、λ3,i和λ4,i,循环迭代次数n;2)while n

4 数值仿真与性能分析

4.1 实验环境与参数设置

为了说明本文所提出的策略的可行性和有效性,本节将通过数值仿真实验对所提出的策略进行评估和分析验证。

一些研究表明,在基于蜂窝下行链路能量收集辅助的D2D通信问题中,当D2D链路的相关参数设置在合理的范围内时,可以从频谱资源块分配、信道选择、发射功率以及SWIPT的时分切换或功率分流因子等方面进行优化,从而解决能量收集的异构网络中D2D链路的通信质量及能效问题[13,17,18]。因此,如无特殊说明,本文均采用文献[13,17,18]中涉及的mmWave信道和功耗模型参数作为仿真实验的参数。仿真场景考虑在一个400 m×400 m的区域内随机部署TX-RX链路,每个期望的TX-RX链路和干扰链路的距离分别是40 m和80 m。在以下对比实验分析中,每个仿真实验值均为独立执行算法100次后所生成的实验数据的平均值。具体参数的设置如表1所示。

Table 1 Simulation parameters setting表1 仿真参数设置

4.2 性能分析与对比

为了比较分析本文所提出策略的性能,将传统的发射功率控制方法作为对比策略。传统发射功率控制能效最大的策略没有考虑SWIPT的功率分流因子的动态联合优化。而文献[13]则是研究了在时分切换模式下EH时隙分配和功率控制的优化策略,在其对比实验中,设置了等分EH时隙的功率控制策略。故而在对比实验中,借鉴文献[13]的对比思想,设置等分的SWIPT功率分流因子的功率控制策略(用PC-E策略表示)与本文所提策略进行比较。

为探究最大发射功率Pmax与能量效率之间的变化关系,实验中对每种策略配置均运行100次来观察能量效率的变化。假设其他参数设置相同,将Pmax分别设置为50 mW,100 mW,150 mW,200 mW和250 mW。实验对比结果如图4所示。

Figure 4 Effect of the maximum transmission power on energy efficiency

从图4中可以看出,在2种策略下,随着Pmax的增加,链路的能量效率也随之增加。这是因为在适当的范围之内,随着Pmax增大,TX的发射功率Pi增大,继而传输吞吐量随之增大,所以链路能效越大。然而,当Pmax达到200 mW后,尽管TX发射功率的增大能带来更大的吞吐量,但此时链路的能耗也随之增大,从而导致链路能量效率随着Pmax增大而呈下降趋势。因此,选择合适的最大发射功率至关重要,从仿真结果来看,在Pmax的设置安排上,需要考虑吞吐量和能量消耗的权衡,才可以获得更好的性能,故在后面的仿真实验中,设置Pmax=200mW(约23dBm)。

图5给出的是最小能量收集阈值Emin对能量效率影响的实验结果图。实验中,设置Emin分别为-20 dBm,-18 dBm,-16 dBm,-14 dBm和-12 dBm。从实验结果可以看出,随着最小能量收集阈值的增大,链路能量效率逐渐降低。这是因为根据热力学第一定律,当从TX上发射的信号功率不变时,如果用于能量收集的功率变大,则用于信息传输的功率会变小,吞吐量从而变小。

Figure 5 Effect of the energy harvesting threshold on energy efficiency

从图4和图5的实验对比结果可以看出,本文提出的功率控制和动态SWIPT功率分流因子联合优化策略在能量效率性能上均优于传统的功率控制策略,同时验证了采用功率分流方式实现SWIPT,可以从能源管理的角度提高D2D通信的能量效率。为了进一步验证本文所提策略的有效性,在后面的对比实验中,借鉴文献[23]的对比思想,增加设置一个采用最大发射功率的动态SWIPT功率分流因子基准策略(用PS-max策略表示),以验证发射功率控制和功率分流因子二者联合优化对于系统能效的影响。

图6比较了3种策略下不同TX-RX链路距离对链路能量效率的影响。从实验对比结果可以看出,随着TX-RX链路距离增大,3种策略的能量效率逐渐降低,这是由于TX-RX之间的路径损耗随着二者之间距离的增大而增大,信道增益随之减小,导致能量效率降低。但是,从纵向比较来看,本文所提策略的性能优于另外2种对比策略,这是因为采用联合发射功率和功率分流因子的动态优化策略可以得到一个最优SWIPT功率分流因子,从而达到链路吞吐量和能耗之间的最优权衡。

Figure 6 Effect of the distance of TX-RX on energy efficiency

干扰链路距离对能量效率的影响如图7所示。实验中,干扰链路的距离分别设置为60 m,70 m,80 m,90 m和100 m。从实验对比结果可以看出,随着干扰链路距离的增大,3种策略的能量效率均有所提升。这是由于随着干扰链路距离的增加,TX-RX链路的信噪比增大,根据香农公式链路吞吐量也随之增大,因此在链路能耗固定的情况下,传输的比特越多,链路能量效率越大。但是,从纵向比较来看,在相同的干扰链路距离影响下,本文所提策略的性能要优于另外2种对比策略,这是因为无论是采用等分的SWIPT功率分流因子的功率控制策略还是最大发射功率策略,都只能达到在链路吞吐量或是能量消耗单方面的性能,而采用本文所提策略可以更好地满足链路在吞吐量和能耗上的平衡,从而达到能量效率最大化。

Figure 7 Effect of the distance of the interference link on energy efficiency

5 结束语

本文对无线携能通信下mmWave协作通信小单元的能效优化问题进行研究。首先,构建了mmWave小单元内能量受限的UE配对后的系统模型。其次,在能量与信息同时传输阶段,为实现同时性,UE的接收端工作在功率分流模式,以最大化链路能量效率为目标,提出了一种基于无线携能通信下mmWave协作通信小单元的能效最优策略。为实现绿色通信的目标,该优化策略在最小链路传输速率和最小能量收集的联合约束下,通过优化发射功率控制和功率分流因子,实现最大化系统链路能量效率的目标。针对原始优化问题是一个具有NP难性质的非凸分式规划问题,根据Dinkelbach方法,将目标函数为非凸的分式规划问题转化为等价的凸形式的减式问题,继而采用常见拉格朗日对偶方法求解等价的凸优化问题,然后设计一个交叉迭代的算法以得出最优解。最后,通过仿真实验,将本文策略、传统功率控制策略和最大发射功率策略做对比,证明了本文所提策略的有效性和优越性。

本文的创新点在于:在能量与信息同时传输阶段的策略中,UE之间采用mmWave进行彼此通信,并创新性地将SWIPT技术应用到UE通信链路之中,通过规划最小链路传输速率和最小能量收集之间的权衡,从而实现UE链路能量效率的最大化。