基于GGInformer模型的多维时间序列特征提取与预测研究*
2024-04-23任晟岐
任晟岐,宋 伟
(郑州大学计算机与人工智能学院,河南 郑州450001)
1 引言
随着大数据、物联网技术及各行业的发展,积累的时间序列数据量非常庞大且复杂。其中,相比单维时间序列数据,多维时间序列数据要更为复杂。多维时间序列数据之间存在着相互依赖的关系,主要包括数据间的时序依赖关系以及多维特征间相互依赖关系。2种关系都会对预测结果产生重要的影响。
早期,对于时序预测任务,研究人员多使用统计学的方法进行研究。Gurland等人[1]提出的自回归滑动平均模型,将自回归过程和滑动平均过程结合起来,使模型更具有普遍性。Box等人[2]提出的差分整合移动平均自回归模型,通过差分变换方法将非平稳化时间序列平稳化,提高了模型性能。Cao等人[3]提出了基于回归分析的线性支持向量回归模型,并将其应用到了金融时序预测领域。Boller-slev[4]提出了广义自回归条件异方差模型,并将该模型推广到更大的回归阶数,解决了自相关系数消退较慢的问题。Ariyo等人[5]将差分整合移动平均自回归模型用于预测股价。基于传统统计学的方法对数据分布规则和完整性等方面要求非常严格,仅考虑了线性变化关系,适用于线性数据,对于非线性、多尺度的时间序列,无法捕捉非线性关系。这使得传统时序预测的方法无法获得较高的预测精度。
随着人工智能的发展,深度学习技术在众多领域都取得了巨大的成就,研究人员也将其应用于时间序列预测。Karim等人[6]将LSTM(Long Short-Term Memory)网络与BP(Back Propagation)神经网络的全连接层结合起来用于多元时间序列分类。Yu等人[7]将图神经网络和时间序列预测相结合,用于交通流量预测。Meesad等人[8]使用支持向量回归SVR(Support Vector Regression)模型对股票数据进行建模分析。Nair等人[9]提出了一种基于粗糙集的决策树系统,使用C4.5决策树和粗糙集进行特征提取和规则总结,基于孟买证券交易所数据进行实验研究。White[10]使用人工神经网络ANN(Artificial Neural Network)对IBM公司的股票进行分析。Selvin等人[11]使用CNN(Convolutional Neural Network)、RNN(Recurrent Neural Network)和LSTM对股票市场进行预测。Kussul等人[12]提出了一种用于交通流预测的深层结构模型,使用堆叠式自动编码器提取交通流特征,并应用逻辑回归层进行预测。李章晓等人[13]将深度学习和进化计算结合起来对外汇进行预测。2020年杨妥等人[14]提出了融合情感分析的SVM-LSTM模型,提高了对股指期货的预测精度。Wu等人[15]结合CNN和LSTM提出了一个混合深度学习框架,用于预测未来的交通流量。Gensler等人[16]提出了结合自动编码器和LSTM网络的预测模型,用于激活各种太阳能预测。Grover等人[17]提出了一种综合方法,将经过鉴别训练的预测模型与深度神经网络相结合,用于联合统计一组天气相关变量。
以上方法针对时间序列预测已经取得了相对较好的结果,然而在处理特征参数复杂、非线性的多维时序数据时仍然存在一定的局限性。多维时间序列存在特征数较多、特征间相关性较差以及特征冗余问题严重的情况,且不同的特征变量对于最终的预测结果会产生不同的影响。对多维时间序列进行特征提取,剔除不相关及冗余的特征,将对提升预测效果产生积极影响。
本文针对多维时间序列特征提取及预测任务提出了GGInformer模型。首先,对遗传算法进行改进,使用类内类间距离作为判断依据计算出每个特征的类内类间距离比值,根据比值初步对数据特征进行提取,同时去除数据集中的不相关特征;然后,利用遗传算法[18]的“优胜劣汰”原则对多维时间序列数据进行全局寻优,进一步去除冗余特征;最终,选择出最优的特征组合用于后续的预测任务。针对长序列时序预测LSTF(Long Sequence Time-series Forecasting)任务中的长程依赖问题与多维时序数据的时序依赖关系,本文通过融合Informer模型[19]与GRU(Gate Recurrent Unit)网络,提升了预测效果。实验结果表明,GGInformer模型可以很好地对多维时序数据进行特征提取与预测。此外,本文还对模型的长序列时序预测能力进行了研究,通过预测不同的时间长度来对模型性能进行评估。实验结果表明,相比于对照模型,本文模型的长序列预测能力也有所提高。
2 GGInformer模型构建
本文结合改进遗传算法、GRU网络和Informer模型构建了GGInformer模型,以此对多维时序数据进行特征提取与预测。该模型首先使用改进遗传算法对多维时间序列数据进行特征提取,减少了不相关特征和冗余特征对后续预测过程的消极影响,同时还可以减少输入到预测模型中的数据量,起到降低计算量的作用。然后,将提取出的特征输入到GRU网络进一步提取数据的全局时序依赖信息。之后,将GRU网络保存的全局时序信息输入到Informer 模型,经过嵌入层、编码器和解码器,最后在全连接层得到预测值。GGInformer模型架构如图1所示。
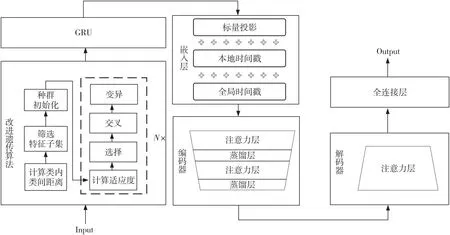
Figure 1 Architecture of GGInformer model
2.1 基于改进遗传算法的特征提取
针对多维时序数据存在特征复杂、特征冗余等问题,本文结合类内类间距离判断依据与传统遗传算法提出了改进的遗传算法。首先,为了剔除数据集中的不相关及相关性较小的特征,本文采用类内类间距离公式计算出每个特征的类内类间距离比值,根据比值的大小对数据特征进行初步提取;然后再利用遗传算法对多维时序数据集进行全局寻优,继续去除冗余特征;最终选出最优的特征组合完成后续预测任务。
基于改进遗传算法的特征选择算法如算法1所示,相关流程图如图2所示。

算法1 基于改进遗传算法的特征选择算法输入:特征选择前的高维时序数据 P∈Rl×m。输出:特征选择后的低维时序数据 B∈Rl×n。Step 1 对多维时序数据P进行数据预处理并随机选择样本数据X;Step 2 利用类内类间距离计算公式计算样本数据的类间离散度矩阵Sb;Step 3 利用类内类间距离计算公式计算样本数据的类内离散度矩阵Sw;Step 4 计算类内类间距离比值J;

Step 5 根据比值J对高维时序数据P进行特征选择,剔除不相关或相关度低的特征,得到数据Y;Step 6 使用遗传算法对数据Y进行二次特征提取,剔除冗余特征,得到数据B。

Figure 2 Flow chart of improved genetic algorithm
遗传算法基本操作包括:基因编码、产生初代种群、进行染色体选择、染色体交叉、染色体变异,不断产生新的子代以寻找最优解。具体设计流程如下所示:
(1)种群初始化。本文对输入的多维时序数据采用二进制编码进行种群初始化,每条数据的每一个特征因子位按照等概率在{0,1}中选择。矩阵表示如下所示:
其中,矩阵中每一行代表一条染色体,ai,xj∈{0,1},其取值为0表示未被选中,取值为1表示被选中,m代表染色体数量。
(2)适应度函数选取。本文选择基于类内类间距离的可分性判断依据作为适应度函数。
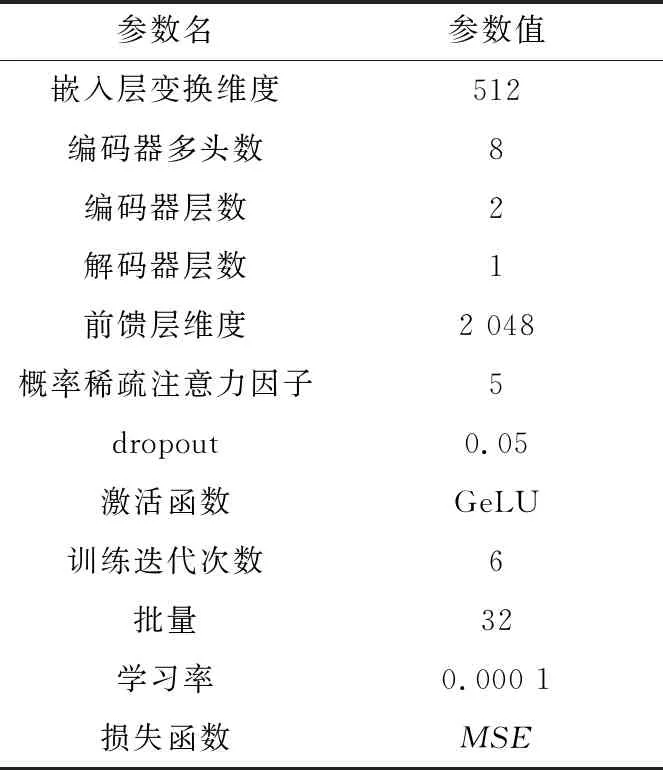
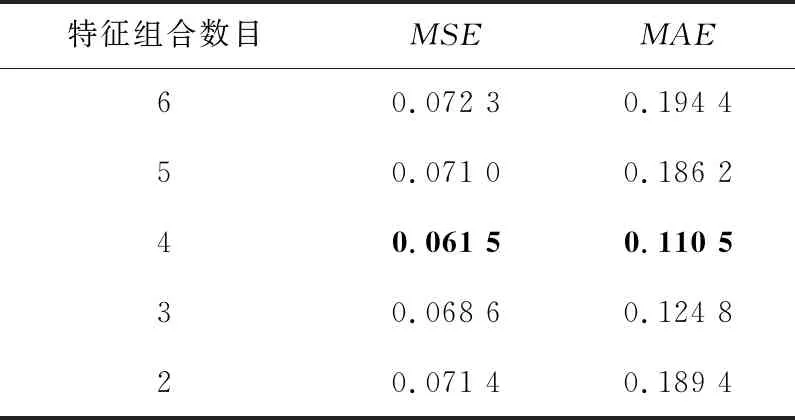
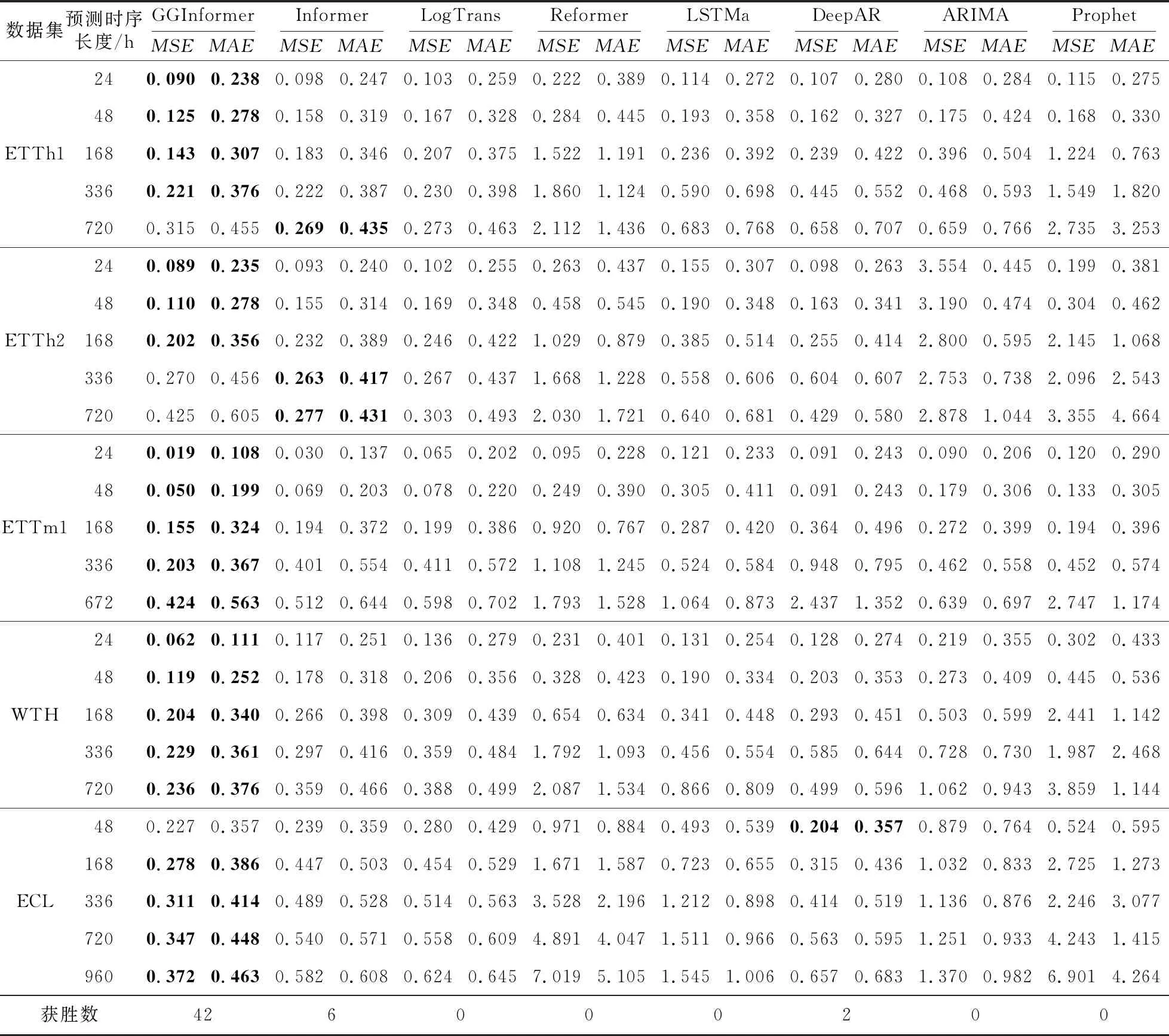
假设从D个特征中选出最优的d个特征(d (1) (2) (3) 其中,tr(Sb)和tr(Sw)表示矩阵的迹。 (3)选择算子选取。确定了适应度函数之后,遗传算法基于适应度值对个体进行评价,为了保证能够选择出适应度最好的个体,有效剔除相关性较差的和冗余的个体,本文使用轮盘赌选择方法作为选择算子选择出最合适的个体。 (4)交叉算子选取。本文采用多点交叉方式作为交叉算子进行交叉操作。在单个个体中随机设置多个交叉点,2个个体间根据交叉点进行基因交换,生成新的个体。 (5)变异算子选取。本文采用单点位翻转突变作为变异算子进行变异操作。随机从种群中选择一个个体,再随机从个体基因中选择一个基因进行翻转变异。 为了解决多维时间序列预测中由于长程依赖导致的时序依赖性较弱的问题,模型需要具有较强的解决长程依赖问题的能力。本文基于Informer模型来构建时序预测模型。此外,为了更好地提取时间序列数据间的时序依赖关系,模型选择GRU网络保存多维时序数据早期的时序信息,以增强后续模型预测能力。模型设计流程如下所示: (1)GRU网络包括2部分:GRU单元和线性单元。为了模型能够更准确地预测,通过实验验证,本文GRU单元选择3层,线性单元选择2层。GRU网络结构图如图3所示。 Figure 3 Structure of GRU of network (2)嵌入层包括3部分:标量投影嵌入、本地时间戳嵌入和全局时间戳嵌入,可为输入数据添加位置向量以及每个时间点的时间信息。其中,标量投影嵌入主要采用一维卷积将输入数据的特征维度向量转换为512维向量;本地时间戳嵌入采用Transformer模型中的位置编码方法;全局时间戳嵌入采用全连接层将输入的时间戳向量映射为512维向量。最后,将标量投影嵌入、本地时间戳嵌入和全局时间戳嵌入三者结果相加,得到最终的嵌入层结果。 (3)编码器包括2部分:注意力层和蒸馏层。其中,在注意力层Informer 模型使用算法2描述的概率稀疏自注意力算法。 算法2 概率稀疏自注意力算法输入:Q∈Rm×d,K∈Rn×d,V∈Rn×d。输出:概率稀疏自注意力特征矩阵 S。Step 1 设置超参数 c,u=c ln m,U=m ln n;Step 2 从K中随机采样U个点积对作为 K;Step 3 计算采样的得分 S=QKT;Step 4 按行计算稀疏性得分 M=max(S)-mean(S);Step 5 按照稀疏性得分M的排序选择前u 个Qi 作为Q;Step 6 计算S1=softmax(QKT/d)·V;Step 7 计算S0=meanV ;Step 8 合并S1和S0,得到最终结果S={S1,S0},并调整为原来的行顺序。 根据算法2的概率稀疏自注意力计算过程可以看出,结果S必然会产生冗余(由于存在S0),因此在编码器中又加入了注意力蒸馏机制,以此来蒸馏出更具有优势的注意力权重。从第j层到j+1层的蒸馏计算如式(4)所示: (4) (4)解码器。解码器的注意力层由一个掩码多头概率稀疏自注意力层和一个多头自注意力层组成。其中,多头概率稀疏自注意力层要进行mask掩码操作,防止自回归。最后连接一个全连接层进行预测。整个解码器的解码过程舍弃了动态解码过程,而采用一次前向过程,即可解码得到整个输出序列,大大缩短了预测时间。需要注意的是,解码器使用的是生成式的推理解码,其输入数据形式如式(5)所示: (5) (5)全连接层。经过Informer模型解码器之后连接一个全连接层进行预测输出。 本文在5个数据集上进行了实验,即用于研究LSTF问题的2个真实数据集和3个公共基准数据集。 电力变压器温度ETT(Electricity Transformer Temperature)数据集:ETT是电力长期部署的一个重要指标。为了探究LSTF问题的粒度,本文选择了不同粒度的数据集,包括以1 h间隔划分的ETTh1和ETTh2、以15 min间隔划分的ETTm1。每个数据点由1个目标值“OT”和6个电力负荷特征组成。训练集、验证集和测试集分别包括12个月、4个月和4个月的数据。 耗电负荷ECL(Electricity Consuming Load)数据集:该数据集包括321个客户端的耗电量。本文设置“MT 320”为目标值。训练集、验证集和测试集分别包括15个月、3个月和4个月的数据。 天气WTH(WeaTHer)数据集:该数据集包含2010年~2013年4年间美国近1 600个地点的当地气候数据,每1 h收集1次数据点数据。每个数据点数据包括1个目标值“wet bulb”和11个气候特征。训练集、验证集和测试集分别包括28个月、10个月和10个月的数据。 为了准确全面地评价模型性能,本文选择平均绝对误差MAE(Mean Absolute Error)和均方误差MSE(Mean Square Error)2种预测评价指标,分别如式(6)和式(7)所示: (6) (7) 为了验证模型的有效性,本文选择了ARIMA[5]、Prophet[20]、LSTMa[21],DeepAR[22],Reformer[23]和LogTrans[24]6种时间序列预测算法及Informer模型与GGInformer模型进行对比实验。在参数的选择与设置过程中,本文通过交叉验证的方法来确定最合适的超参数设置。改进遗传算法和Informer模型有关超参数设置分别如表1和表2所示。此外,GRU网络隐藏层维度设置为64,GRU网络层数设置为3。 Table 1 Super parameters setting of genetic algorithm Table 2 Super parameters setting of Informer model (1)基于类内类间距离的特征选择结果分析。 为了验证类内类间距离的有效性,本文以WTH数据集为例,使用类内类间距离对WTH数据集进行特征选择。首先,计算WTH数据集的类内类间距离比值大小J。然后,根据J的大小,选择大于阈值的特征,去除小于阈值的特征。本文阈值取比值J的最大值与最小值的均值。最后,将选择出的特征进行组合,用来指导后续遗传算法的特征优化。基于类内类间距离的WTH数据集的特征选择结果如图4所示。 Figure 4 Feature selection results on WTH dataset based on intra class and inter class distances 由图4可以看到,WTH数据集的12个数据特征中,部分特征的类内类间距离比值较小,说明其特征相关性较弱。根据图4选择大于阈值0.000 079的特征,得到特征序列号为1,3,4,6,7,10和12的7个特征进行组合。选择出的7个特征类内类间距离比值结果较大,说明其特征间的相关性较强,组成的特征组合可以对后续特征提取与预测产生积极的影响。 (2)基于改进遗传算法的特征选择结果分析。 在上述根据类内类间距离比值筛选出来的特征的基础上,继续使用改进遗传算法进行特征提取,以此消除冗余特征的消极影响。经过种群初始化、选择复制、交叉、变异等过程,数次迭代优化后选择出最优的特征组合。 由于不同特征对最终的预测结果会产生不同的影响,因此特征数对于多维时序预测来说也是一个重要影响因素。为了测试特征数对预测结果的影响,本文仍以WTH数据集为例进行研究,对选取的7种特征使用遗传算法再进行特征提取,分别提取2种,3种,4种,5种和6种特征组合进行实验对比,实验结果如表3所示。 Table 3 Prediction results based on genetic algorithm feature selection 从表3可以看出,当WTH数据集通过遗传算法选择的特征组合数为4时,预测结果的MSE值和MAE值均达到最小值0.061 5和0.110 5。由此可以得出,WTH数据的最优特征组合是通过遗传算法选择出的4种特征的组合。 为了验证GGInformer模型预测的有效性,本文在5种数据集上进行对比实验,结果如表4所示。为了测试模型处理LSTF问题的能力,本文逐步延长了预测窗口大小,即在ETTh1、ETTh2、ECL和WTH几种数据集中分别预测24 h,48 h,168 h,336 h,720 h和960 h的结果。在ETTm1数据集中分别预测6 h,12 h,24 h,72 h和168 h。 Table 4 Time series forecasting results on five datasets 从表4中可以看出,GGInformer模型的预测能力相比于Informer模型的有显著提升,主要体现在GGInformer模型的获胜结果数,即GGInformer模型在5种数据集上的获胜结果数为42,远大于Informer模型的获胜结果数6,说明Informer模型在预测训练过程中虽然相比于LogTrans等模型有了明显提升,但是还是会受到多维时序数据的复杂度以及长程依赖问题的影响。本文在Informer模型的基础上结合改进遗传算法和GRU网络有效地提升了预测的性能,消除了不相关特征和冗余特征的消极影响,并通过GRU网络保存数据的全局时序信息,进一步提高了模型的预测精度。 需要注意的是,虽然GGInformer模型的预测结果整体上相比Informer模型的较有优势,但是在ETTh1和ETTh2 2种数据集上的较长序列(336 h,720 h)的预测结果却有一定的差距。为了探究原因,本文将上述2种数据集与ETTm1数据集进行对比分析,发现GGInformer模型在ETTm1数据集上的长序列预测能力优势很明显,说明GGInformer模型的长序列预测能力会受数据集划分粒度的影响,划分粒度越大,其时序依赖性越弱,预测起来难度越大。 此外,本文还发现,在ECL数据集上,在较短的时序上(≤336 h),DeepAR 模型的预测能力相比于Informer模型的要好,说明在个别特殊的数据集上Informer模型的短距离时序预测能力不强。但是,将DeepAR模型的预测结果与GGInformer模型的对比后可以发现,在预测时序长度为168 h和336 h时,GGInformer模型的MSE值和MAE值明显降低,且优于DeepAR模型的。上述结果说明,GGInformer模型相比Informer模型可以更有效地增强短距离时序预测能力。 为了验证改进遗传算法和GRU网络对GGInformer模型预测能力的提升效果,本文对其进行了消融实验。以WTH数据集为例,相关消融实验结果分别如表5和表6所示。 Table 5 Ablation experiment results of improved genetic algorithm Table 6 Ablation experiment results of GRU network 本文将GGInformer模型与GRU+Informer模型的预测结果进行对比,预测时序长度选择24 h,168 h和720 h。相比GRU+Informer模型,GGInformer模型预测结果的MSE分别降低了22%,10%和28%。这说明多维时间序列数据集中不相关特征和冗余特征对时序预测会产生消极影响,本文提出的改进遗传算法可以有效解决多维时序数据特征间的相关性较差以及特征冗余的问题。 本文将GGInformer模型与GA+Informer模型的预测结果进行对比,预测时序长度同样选择24 h,168 h和720 h。相比GA+Informer模型,GGInformer模型预测结果的MSE分别降低了29%,10%和22%。上述结果表明,对于时序预测任务,时间序列数据间的时序依赖性学习同样很重要,GRU网络可以有效提取时序信息的全局依赖性,通过保存全局时序信息进一步增强后续模型的时序预测能力,从而有效地解决了多维时序数据在预测过程中由于时序依赖性较低导致的长程依赖问题。 为了进一步验证本文模型对于不同类型多维时间序列数据预测的通用性,本文选择了浦发银行(SPDB(Shanghai Pudong Development Bank),sh60000)从2010年7月1日~2020年7月31日共10年的股票价格历史数据进行实验分析。在实验过程中,模型设置同上述实验过程的相同,在真实数据上预测时不需要在特定数据集上进行预训练。具体实验结果如表7所示,GGInformer模型预测结果与实际值的拟合曲线如图5所示。实验表明,改进遗传算法通过特征提取去除了数据不相关特征和冗余特征,提高了预测准确度,结合了GRU网络的模型又进一步提高了预测结果。 Table 7 Prediction results of SPDB stock price Figure 5 Results of SPDB stock price prediction 本文主要研究多维时间序列数据的特征提取与时序预测问题。针对多维时间序列数据存在特征间相关性较差及特征冗余的问题,以及由于时序数据间时序依赖性较低导致的长程依赖问题,本文提出了GGInformer模型。为了验证该模型的有效性,本文在5种多维时间序列数据集上进行了对比实验,并通过消融实验验证了模型解决上述问题的有效性。此外,还在不同类型数据集上进行了实验,最终的实验结果和可视化分析均表明,本文模型在多维时序预测任务中具有较好的通用性和普适性。
2.2 基于GGInformer模型的时序预测


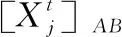
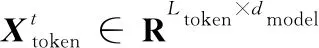
3 实验设计
3.1 数据集
3.2 评价指标
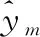
3.3 对比模型与超参数设置

4 实验结果分析
4.1 改进遗传算法特征选择结果分析

4.2 预测结果分析
4.3 消融实验分析


4.4 浦发银行股票数据实验


5 结束语
