数据中心集群灵活边界下电力系统分布鲁棒优化调度方法

张 锞，王 旭，杨宏坤，蒋传文

（1.电力传输与功率变换控制教育部重点实验室（上海交通大学），上海市 200240；2.上海非碳基能源转换与利用研究院，上海市 200240）

0 引言

“东数西算”工程启动建设国家算力枢纽节点，规划了10 个国家级互联网数据中心（Internet data center，IDC），并引导可再生资源丰富地区配合绿色能源形成IDC 集群［1］。预计至2024 年，IDC 新增投资规模超1 100 亿元［2］。到2030 年，中国IDC 耗电量将突破400 TW·h，占全社会用电总量的3.7%［3］。

可再生能源、储能、IDC 等海量分散与难观难测分布式资源的接入为电力系统调度带来了新挑战［4-5］。海量分布式资源因差异化的响应特性而难以采用统一数学模型对其进行刻画，分布式资源的聚合管理问题得到了许多关注［6-7］。文献［8-9］分别基于频谱聚类算法和资源时域特性与多交易品种契合度指标指导分布式资源分类聚合。但算力资源与辅助设备能耗之间的内生关联性及光储等分布式资源的调节特性差异，极大增加了IDC 集群聚合体（IDC cluster aggregator，ICA）调节能力可信等值表征的难度。

同时，集中式绿色能源的强波动性和高随机性也使得电力系统运行复杂性进一步提升［10］。针对电力系统运行不确定性问题，常用的处理方法主要包括随机优化（stochastic optimization，SO）和鲁棒优化（robust optimization，RO）。SO 主要依靠概率分布处理随机参数［11-14］。然而实际中真实概率分布难以获知，导致该方法样本外表现（out-of-sample guarantee）较差。RO 假定随机参数概率分布未知而使用其波动范围，无法充分利用历史数据导致调度结果冗余度大［15］。通过结合统计学与优化理论，数据驱动分布鲁棒优化（data-driven distributionally robust optimization，DDRO）克服了前述两种方法决策结果在全概率区间上适应性较差的问题，在机组组合［16-17］、综合能源系统［18］、分布式资源聚合优化运行［19］等领域均有应用。然而，目前DDRO 仍面临随机变量概率分布模糊集构建和优化模型快速求解两个难题。

根据模糊集的形式对DDRO 问题进行分类。文献［20-21］采用矩信息表征随机变量整体特性，只能捕捉到真实分布的部分信息。基于概率距离的不确定集则主要利用概率密度信息，构建以经验分布为中心的概率空间上的一个球形模糊集，能够弥补矩信息不确定集计算困难的缺陷。相较于KL（Kullback-Leibler）散度［22］和JS（Jensen-Shannon）散度［23］等概率距离，Wasserstein 距离在两个分布重叠极少时仍能有效反映其远近，保证了所构建模糊集的样本外表现［24］。然而基于该模糊集的DDRO 问题中不确定变量的指数增长带来了维数灾难［25］，Benders 分解方法［26-27］、对偶原理［28］等传统方法求解速度较慢，近似处理能够将该问题转化为更易处理的结构［29］。但有限适应性［30-31］和线性决策准则［32］等已有方法普遍近似误差较大且难以计量［33］。

综合上述问题，本文通过刻画不可调风电资源不确定性特征与挖掘分布式资源聚合体多维度灵活调节潜力，提升电力系统应对集中式不可调资源不确定性的能力。首先，本文对算力资源弹性调度带来的IDC 电力负荷动态变化特性进行精细化表征，在此基础上提出ICA 外特性参数动态辨识方法，保证其聚合最优性与分解可行性。然后，利用历史数据得到契合风电出力特性的∞-Wasserstein 模糊集，构建了两阶段DDRO 电力系统调度模型，促进电力系统运行安全性与经济性平衡。最后，利用近似算法将两阶段分布鲁棒调度模型转化为商业求解器可快速求解的有限维问题，并通过仿真验证了所提方法的有效性。

1 ICA 调度可行域边界辨识方法

在介绍ICA 调度可行域边界辨识方法前，先定义两个概念:1）灵活性资源聚合是指将海量分散、难观难测的灵活资源集中调控以缩小系统运算规模；2）灵活性资源聚合体调度可行域边界辨识是指考虑内部异构设备及网络运行等约束，从聚合体层面计算整体功率时变柔性极值，构建内部资源运行方式与聚合体外特性表现的映射关系。该方法能够利用广域分散资源灵活性变化规律挖掘其调控潜力，为后续建模提供聚合体外特性参数。本章首先构建IDC 及配套光储能耗模型并形成ICA，然后采用自适应鲁棒优化（adaptive robust optimization，ARO）方法解决ICA 调度可行域边界辨识问题，所得结果同时具备聚合最优性和分解可行性［34］。

1.1 IDC 数据负载能耗模型

IDC 整体能耗可分为设备自身能耗、数据负载能耗、配套光储建模3 个部分。

1.1.1 基于动态电压频率调节（DVFS）技术的设备功耗模型

IDC 自身能耗主要来自负责数据处理及交互通信的信息技术（IT）设备功耗、防止设备过热的冷却装置能耗及高可靠性的配电设备能耗，且冷却设备、配电设备能耗与IT 设备功耗间具有强相关性如下:

式中:Ne为服务器总数量；PIDC，t为t时段IDC 自身能耗；PIT，e，t、PCO，e，t、PDV，e，t分别为t时段服务器e的IT设备功耗、冷却装置能耗、配电设备能耗；ηPUE，e为服务器e的IDC 能源效率（power usage effectiveness，PUE）。

服务器功率为固定功耗与中央处理器（CPU）功耗之和，IT 设备功率则为运行服务器功率的总和，可表示为:

式中:PDVF，e，k为t时段服务器e的固定功耗；PCPU，e，k，t为t时段IDC 内k型服务器e的CPU 功率；Nk为总服务器数目；Me，k为在线运行服务器数；KF为CPU 功耗系数；be，k，t，s为t时段IDC 内k型服务器e处理的数据负载量关联的变量，下标s表示对应挡位工作频率标志位；fCPU，e，k，s为对应工作频率。

采用DVFS 技术［35］，IT 设备CPU 可通过灵活调节工作频率以提高效率。因此，CPU 运行功率与其工作频率相关［36］。

1.1.2 数据负载能耗

根据不同类型数据的算力需求，可在服务管理的过程中将数据负载划分为时延敏感型和时延容忍型两类。时延敏感型负载有严格的处理时间要求，时延容忍型负载则允许在容忍时间内处理。利用时延容忍型负载的时间调节特性优化算力需求处理策略可有效协调“算力-电力”调度［37］。

各类型数据均需在容忍上限时长td内完成处理。t时段ρ类型时延容忍型负载i转移量Δλi，ρ，t与已完成任务di，ρ，t的总和应满足总时延容忍型负载处理需求λi，ρ，且任务结束时段T挂起任务量φi，ρ，T应回归初始运行t0时挂起任务量φi，ρ，t0。数学表达式如下:

式中:NDTL为时延容忍型负载总量；Nρ为数据类型总和；为在容忍上限时长td内ρ类型数据需完成的数据处理量；Δt为时间的有限变化量；φi，max为可挂起的任务量上限。

1.1.3 配套光储模型

屋顶光伏及储能设备协同辅助保障IDC 持续稳定的供电需求，降低用电成本并提升清洁能源利用率。光伏及储能约束分别如式（6）和式（7）至式（12）所示。

式中:PPV，n，t为t时段光伏n的功率；和分别为t时段储能设备s的充、放电功率；下标max 和min 分别为对应参数的上、下限；ut表示t时段火电机组开关机状态；和分别为储能设备s的充、放电效率；SES，s，t为t时段储能设备s的荷电状态（state of charge，SOC）；S为储能设备集合；和分别为储能充、放电效率。式（6）与式（7）、式（8）分别为光伏设备出力及储能充放电上下限约束；式（9）要求储能在一个工作周期中始末状态保持不变；式（10）和式（11）为储能荷电状态约束；式（12）要求储能装置同一时段仅充电或放电。

1.2 基于ARO 的调度可行域边界辨识模型

基于ARO 的灵活性聚合体调度可行域边界辨识模型如下:

式中:Dp为调度可行域；V(Dp)为调度可行域范围；p0为聚合有功功率；x(·)为ICA 内部资源调度方案；l为各类资源约束；L 为约束索引集；D、El、W、g、w、sl均为系统参数。

目标函数式（13）旨在寻找ICA 最大调度可行区域。式（14）为有功线性近似潮流模型，其中，x(p0)仅包括ICA 内部可调资源，不可控资源则视为给定的系统参数。式（15）包含时延容忍型数据负载、屋顶光伏及储能设备等聚合体内部设备的功率容量约束式（5）至式（8），储能SOC 等式约束式（9）至式（12）重构为不等式（16）。式（17）要求对于可行域Dp内的任意有功功率p0，必须存在相应的可行调度方案x(p0)在满足所有运行约束的前提下实现调度指令，由此保障所得结果的分解可行性。

为提高求解效率，使用决策变量p0描述可行域Dp，得到总有功功率可行域使用时间解耦型可行间隔Dp:

通过控制权重ξt的变化，ARO 模型关于p0的约束∀p0∈Dp被转化为关于ξt的约束∀ξt∈G1，其中，G1为盒式不确定集，如式（20）所示。

由此，在一般ARO 模型式（13）至式（17）的基础上，本文构建灵活性资源聚合调度边界（flexibility aggregation boundary，FAB）辨识模型以求解灵活性最大化的ICA 有功功率可行域Dp，如式（21）所示。

FAB 模型第1 阶段目标为最大化总体聚合灵活性，决策变量为()。当ξt的值确定后，第2 阶段目标函数在G1最劣场景下寻找最优可行分布式能源调度策略。由此，在可行域最优性的同时也保证了其分解可行性。

1.3 FAB 模型柔性功率分解方法

为使ICA 作为聚合体参与电力调度，求解FAB模型获得ICA 最优调度可行域边界后，需要制定满足指令在可行域内（即）的ICA 调度计划。柔性功率分解目标为在尽可能完成计划调度方案的前提下使ICA 总成本最小化。通过求解式（22）可得聚合体内部设备级调度指令。具体模型如下:

式中:Ct(xt)为t时段调度方案xt的ICA 系统运营成本函数。

2 风电不确定性描述

本章首先构建∞-Wasserstein 模糊集，然后研究其置信半径选择方法，为基于该不确定集的调度模型提供鲁棒性与经济性的平衡调节依据。

2.1 ∞-Wasserstein 模糊集构建

准确描述风电不确定性能够提升调度结果的精确性。本文提取实际调度系统中大量可用历史数据，通过数据驱动建立∞-Wasserstein 不确定概率分布集合，对风电波动性进行量化约束。该方法在以较高置信度包含潜在随机变量真实概率分布的同时，最大限度地缩小模糊集范围，排除少数极小概率分布，从而避免决策过度保守。因此，其具有良好的随机变量概率分布描述能力，生成的模糊集对样本集以外数据仍具有良好的拟合能力，能够为DDRO问题提供全概率区间支撑的不确定集。

一个概率分布的支撑集是随机变量ζ所有可能值组成集合的闭包。支撑集的每一个元素都包含在超集Ξ 中，而超集可能包含支撑集没有的元素，即Pr(ζ∈Ξ)=1，其中，Pr(·)为概率函数。多面体集Ξ能够利用已有信息排除可能导致结果过度保守的极端场景。由于实际上几乎无法从有限的历史数据集中提取风电的真实概率分布，假定随机变量ζ支撑集未知，信息仅来源于样本历史数据及不确定量支撑集的保守超集Ξ。

本文在经验分布周围建立Wasserstein 不确定集，并认为模糊集以一定的置信度包含了风电的潜在真实分布。Wasserstein 模糊集表达式如下:

式中:εN为所提模糊集置信半径；Pset为概率分布集合；为风电随机变量；ζ和^分别为服从潜在真实概率分布P与经验概率分布的随机参数；为概率分布P和之间的c阶Wasserstein 距离；γ为P与的联合分布；Π为所有可能的联合分布γ的集合。

不同的c值可以得到对应的c-Wasserstein 距离。文献［38］证明∞-Wasserstein 模糊集实际是一个由不确定量组成的混合分布P=，其中，J为场景集合，|J|为场景数，Pj为场景j的概率分布。对于任意场景j，随机变量分布都满足P∈Pset，且在一定置信度下，模糊集中任意概率分布到真实分布的Wasserstein 距离都处于对应置信半径内。因此，可以用如下形式来表征风电概率分布，所提模糊集F(εN)具体如下:

式中:u为辅助变量；和分别为变量ζ的上限值和场景j对应的经验分布采样值；EP( ·)为概率分布P的期望算子。

2.2 模糊集置信半径选择方法

模糊集半径的选择对不确定性描述准确性尤为重要，可以通过半径置信度控制DDRO 模型的保守性。文献［15］中使用的半径确定方法在文献［39］中被证明其结果过于保守而不能体现出DDRO 相对RO 的优越性，为避免后续运行决策过于保守，本文采用改良的Wasserstein 半径确定方法，表示如下［40］:

式中:C为系数；Nw为样本数；β为置信水平。

其中，系数C可由如下优化问题求解得到:

式中:α为优化问题的决策变量；N为随机变量样本数；为历史样本平均值；为随机变量为第o个样本值。式（26）所示针对α的优化问题求解过程可见附录A。

3 电力系统两阶段DDRO 模型构建

3.1 考虑风电不确定性的电力系统运行模型

DDRO 模型通过在最劣概率分布下寻求最优解，保障优化结果是真实样本分布下的性能下界。本文围绕历史数据点构建不确定性集，寻找随机变量ζ在∞-Wasserstein 模糊集上朝着最恶劣场景变化时经济性最优的调度方案。含风电电力系统优化调度运行目标为最小化基准风电预测场景下的电力系统运行成本及最劣概率分布下灵活资源期望调节成本。该系统第1 阶段调度考虑火电启停成本、机组调节成本及机组第1 阶段出力成本；第2阶段考虑ICA 调节成本CICA、火电机组实际运行成本及弃风失负荷惩罚Ccur，l-。具体模型如下:

式中:pg为火电机组g发电机调度计划；ug为火电机组g启停状态为预测风电功率；r+和r-分别为第2 阶段火电向上、向下调节量，和为其对应成本系数；zon和zoff分别表示火电机组启、停动作为第1 阶段调度计划；为第1 阶段预留调节容量；w为实际风电功率；Q(·)为第2 阶段目标函数；Son和Soff分别为火电机组启、停成本系数；zon，g，t和zoff，g，t分别表示t时段火电机组g的启、停动作；ug，t为t时段火电机组g启停状态；ag、bg和cg为火电机组g发电成本系数；PG，g，t为第1 阶段t时段火电机组g计划输出功率；和分别为ICA 第1 和第2阶段向上、向下调整功率，为其对应成本系数；Pcr，w-和Pcr，l-分别为弃风、失负荷量，和为其对应成本系数；为第2 阶段t时段火电机组g实际输出功率；GT、CL、W、D分别为火电机组、失负荷l-、弃风电机组w-及ICA 中可控负荷dtl的集合。

由于风电机组运行费用低廉但难以调节，目标函数中不涉及风电费用，以保证模型优先利用可再生能源。第2 阶段目标函数Q(ug，，w，u)表征在给定机组组合及实际可再生能源出力下系统最优实际运行成本和运行风险之和，包括火电调节成本、ICA 调节成本及弃风削负荷惩罚。

式（35）至式（38）分别代表火电出力上下限、爬坡、启停及可调节容量约束；式（39）为风电出力约束；式（40）为1.2 节所提模型得出的ICA 调度可行域边界辨识约束；式（41）和式（42）为弃风削负荷上下限约束；式（43）为火电机组功率调整约束；式（44）为系统功率平衡约束。值得注意的是，1.2 节和1.3 节所提FAB 模型求解结果满足ICA 约束式（1）至式（12）以保障分解可行性。因此，电力系统两阶段鲁棒模型无须重复考虑相关约束，有效降低了DDRO问题约束规模及求解难度。

3.2 优化模型紧凑处理

两阶段分布鲁棒优化协同调度紧凑数学模型见式（45）。给定第1 阶段决策变量x，模型在随机变量ζ最劣概率分布下寻找第2 阶段决策变量y对应最小期望值。

式中:g(·)表示不等式约束；h(·)表示等式约束。

∞-Wasserstein 模糊集上的DDRO 问题实质上等价于一个多重不确定集上的鲁棒优化问题［27］。基于2.1 节所提概率分布模糊集式（24），将上述优化问题紧凑形式（式（45））重新表述如下:

式中:c为目标函数的系数矩阵；T、W为不等式约束的系数矩阵；m(ζ)为仿射函数。

为不失一般性，本文假设针对第1 阶段决策的任何确定性线性约束都嵌入第2 阶段目标函数中。第2 阶段目标函数由式（47）给出:

式中:q为目标函数系数。

两阶段决策变量x、y具体表达式如下:

4 分布鲁棒近似求解方法

DDRO 模型内层考虑最劣概率分布下最小化目标函数Q(x，ζ)，即在模糊集下对所有随机变量ζ求解对应第2 阶段决策变量y(ζ)，该无限维问题会带来巨大的计算负担。为将降低该优化问题求解规模，本章提出基于重叠线性决策准则的自适应多面逼近（overlapping linear decision rule based adaptive multifaceted approach，OLDR-AMFA）近似算法，将原问题重构为有限维且易于求解的模型。

近似求解方法的核心思想是将追索变量y限制到比原可行域更小的空间，即构建一个有限的第2阶段决策变量空间。假设上述原问题为P，近似后问题变为，近似后所得结果是次优解，即minP≤。下面首先介绍标准单策略线性决策准则（single-strategy linear decision rule，SLDR）近似方法，最后推广至所提算法。

4.1 SLDR 逼近方法

当第2 阶段决策变量y为关于随机变量ζ的函数时，原两阶段优化问题式（46）可转化为:

结合逼近法的思想，采用SLDR 缩小第2 阶段决策变量y的可行域范围Π，可得式（50）所示基于SLDR 的近似问题:

决策变量矩阵中，极弱相关的不确定因素值始终为零。因此，随机变量的部分子集从中被移除，变量及约束数量减少。尽管第2 阶段可行域范围Π小于y的函数空间，但任意使得可行的第1 阶段决策变量x对P同样可行。因此，目标函数最优值为P的上界逼近。虽然追索变量可行域的缩小使得相对原问题P求解难度大幅降低，但同样也使得部分原问题P第1 阶段可行解被排除，导致所得第1 阶段可行解可能少于P实际可行解。SLDR 逼近法近似目标函数所得估计值与实际最优值间的差值非常大且偏差程度难以衡量［41］。上述原因导致SLDR 求解结果过于保守。本文所提OLDR-AMFA 方法能够针对模糊集灵活采用不同追索策略以更加迅速地找到局部最优的追索策略，从而在计算速度提升的同时，避免计算结果过于保守。

4.2 OLDR-AMFA 求解方法

继承限制追索变量可行域的逼近法思想，扩展延伸得到OLDR-AMFA 算法所得近似问题，如式（51）所示。

本文所提OLDR-AMFA 逼近求解思想如图1所示。其中，图1（b）中的OLDR 近似方法几何展示表现为追索可行域自适应多面切割。相对于图1（a）中的SLDR 近似单方向切割示意图，本文所提算法能够针对不同的不确定性集灵活采用不同追索策略找到局部最优的追索策略。

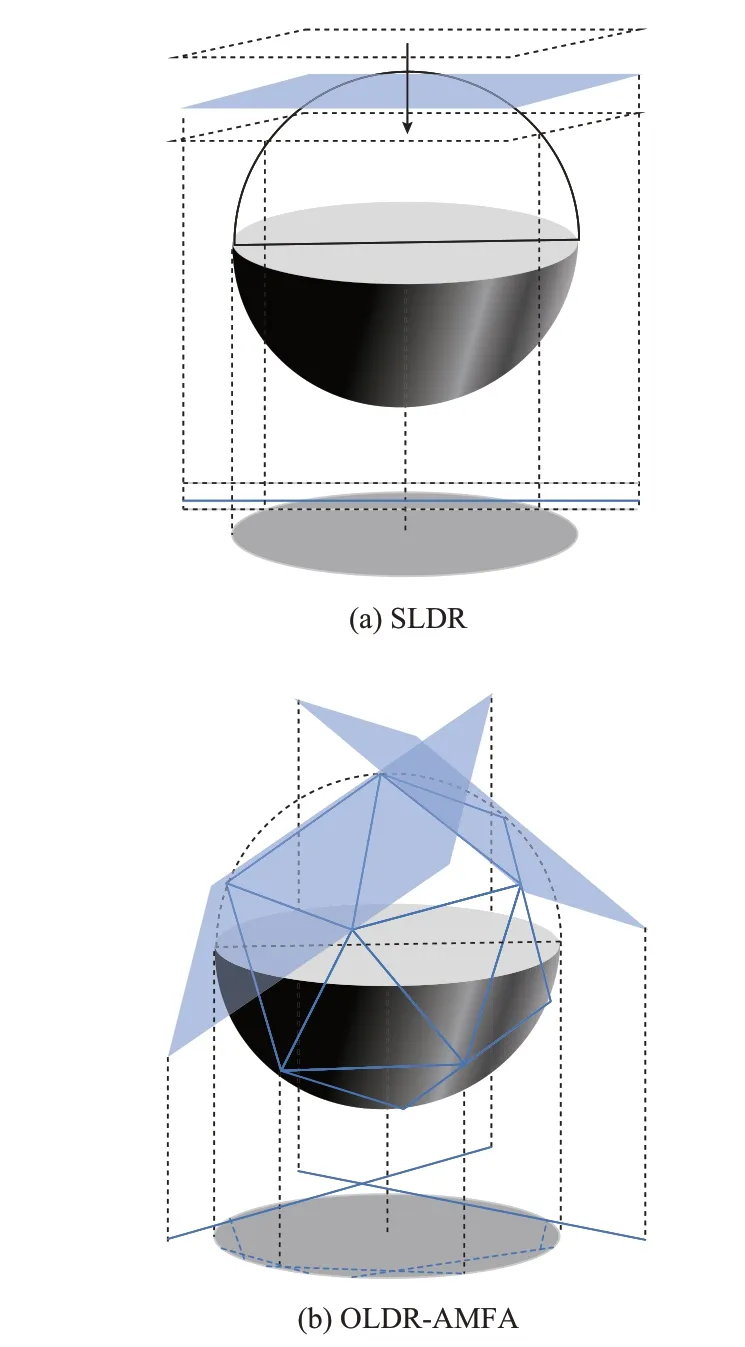
图1 DDRO 逼近求解思想图解Fig.1 Visualization of solution idea for DDRO approximation

考虑所提∞-Wasserstein 模糊集，将OLDR 追索策略yo代入式（46），使用拉格朗日对偶原理，被重构为一个商业求解器可解的有限维线性优化问题如下:

式中:上标“0”表示相应变量的初始值；Y为决策变量矩阵；θ和φ为对偶变量；为保守超集系数；ej为特征矩阵的第j个向量；θo，j和φo，j为样本o的第j个对偶变量；G和M为系数矩阵。

5 算例分析

5.1 算例设置

本节选取修改后的IEEE-RTS 24 节点系统［42］，验证所提两阶段分布鲁棒优化协同调度模型及近似求解方法的有效性，拓扑结构如附录C 图C1 所示。仿真实验所用计算机CPU 为AMD Ryzen 7，内存为8 GB，采用Python 3.8 及RSOME 工具［43］求解。该系统接入装机容量为200 MW 的风电场和总容量为200 MW 的ICA，分别位于节点3 和15。弃风、弃负荷惩罚价格均为800 美元/（MW·h）。火电机组成本系数及网络基本参数见文献［44］，机组调节价格设置参考文献［45］。风电历史数据来自PJM Data Miner［46］。

5.2 ICA 调度可行域边界辨识结果

考虑IDC 总容量为200 MW，配备总装机容量为50 MW 的光伏设备和20 MW 的储能设备。储能初始SOC 为50%，充放电效率为95%。IDC 服务器参数见文献［36］，时延容忍型数据负载占总负载比例为30%。

基于1.2 节所提FAB 模型，得到灵活性最大化的ICA 聚合可行域，并与线性叠加方法辨识结果对比如图2 所示。其中，负值表示ICA 对外提供灵活性支撑。对于大部分时间断面，线性叠加方法所得调度可行域显著大于FAB 模型所得可行域，这是由于线性叠加方法未能考虑算力资源与辅助设备能耗之间的内生关联性以及光储等分布式资源的调节特性差异导致设备边际出力能力的时域耦合关系。结果进一步证明，所提FAB 模型充分考虑了聚合体内部各资源出力情况时间耦合特性，相比线性叠加方法对ICA 聚合灵活性的描述更为精确，有利于挖掘算力负载与电力设备灵活性，为考虑ICA 的电力系统调度策略提供技术参数。

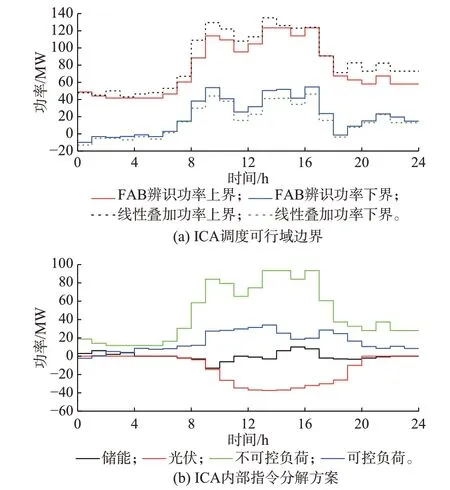
图2 ICA 内部资源时变功率边界Fig.2 Time-variant power boundary of ICA internal resources

5.3 电力系统DDRO 协同调度结果分析

本节对第4 章所提电力系统两阶段协同调度方法进行仿真分析。所提DDRO 模型第1 阶段决策首先基于∞-Wasserstein 模糊集考虑风电潜在真实分布并以此作为基准预测结果，在此前提下确定机组组合、火力发电机组发电计划及ICA 用电计划。当得到实时风电出力数据后，系统通过火电机组向上/向下出力调节、ICA 灵活性支撑、弃风削负荷等手段平衡系统运行状态，即进行各类灵活资源第2 阶段调度。在总体运行成本最小的情况下，确定两阶段最终调度结果。

针对有无ICA 参与电力系统调度的两种结果进行对比分析，见附录C 表C1。对比两种场景所得运行成本及预留调节容量，在有IDC 参与的情况下第1 阶段火电调度成本下降了22 640 美元，火电机组预留调节容量向上减小了17.14 MW，向下降低了10.94 MW，并且运行总成本降低了26 403 美元。运行结果表明在ICA 参与调度的情况下电力系统第1 阶段调度成本及火电机组所需向上/向下调节容量均高于ICA 参与调度的情况，验证了ICA 具备一定的可调度性与支撑能力，在本文所提DDRO 调度框架下能够一定程度上降低电力系统运行成本。

针对某一实际风电场景下分析所提模型平抑风电偏差调度结果，如图3 所示。ICA 响应量、火电机组调节量正值分别表示ICA 增大聚合体用电量及火电机组调用向下调节容量，从而平抑风力发电偏差量。在火电机组日前机组组合、预留调节容量及ICA 日前用电计划确定的情况下，ICA 及火电机组根据风电实际情况确定其出力调整。在凌晨时段风电超发，此时火电机组以较低发电水平的状态运行。因此，预留向下调节容量的能力受限，而ICA能够通过大量充电与将部分算力任务迁移至该时段处理，使得自身用电负荷增加，为电力系统补充了一定的灵活性。在9 h 与10 h 时，ICA 提供了一定减小自身用电量的能力，但由于此时风电波动不大，ICA实际响应量较小。在17 h 后出现了较长时间的风电欠发情况，ICA 通过储能放电并转移时延容忍型负载以降低用电量，验证了ICA 在电力系统中具备辅助平衡可再生能源不确定性，增强系统灵活性的作用。

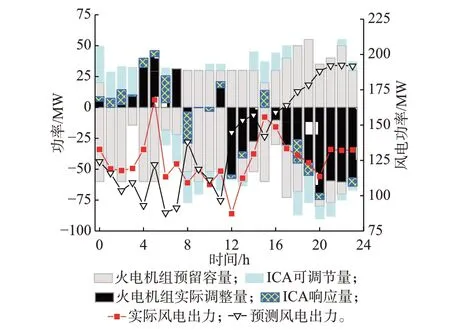
图3 风电实际场景下的调度方案Fig.3 Scheduling scheme in actual wind power scenario

5.4 模糊集契合度验证及半径置信度影响分析

本节对所提基于∞-Wasserstein 模糊集的DDRO（以下简称∞-W-DRO）模型与如下模型运行结果进行对比验证:

1）I-DRO:基于区间（interval-based）构造不确定量模糊集的分布鲁棒优化；

2）M-DRO:基于矩信息（moment-based）构造不确定量模糊集的分布鲁棒优化，其中1-M-DRO 和2-M-DRO 分别表示一阶矩和二阶矩信息模糊集；

3）W-DRO:本节选取半径置信度为20%、50%、70%、90%并记录对应计算时间与系统最优运行成本如表1 所示，探究模糊集半径置信度对电力系统调度结果的影响。表中:1-W-DRO 和2-WDRO 分别表示一阶、二阶Wasserstein 模糊集。

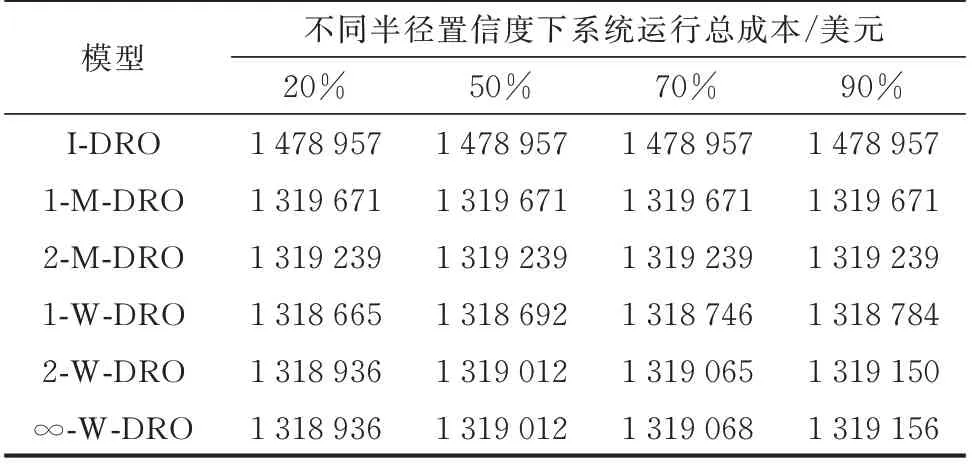
表1 模糊集性能对比Table 1 Comparison of fuzzy set performances

由表1 可知，采用区间刻画不确定性的I-DRO运行成本远高于90%置信度下的W-DRO，这是因为I-DRO 忽略了经验概率分布可提供的有效信息，对风电波动性的描述较为粗糙，考虑最劣场景下的模型决策结果过于保守。基于1-M-DRO 运行结果高于2-M-DRO 运行结果，同时两者都略高于1-WDRO。这是由于一阶矩模糊集仅关心均值而没有考虑数据的变异性，为了确保鲁棒性，基于一阶矩的优化结果可能会对所有可能的情况都过度应对。而二阶矩模糊集同时考虑了数据的中心位置和分散程度，从而更精确地应对不确定性并提供相对平衡的解决方案。相对于矩信息模糊集，Wasserstein 模糊集捕获了分布的整体特性而不仅仅是部分统计特性，1-W-DRO 运行成本在M-DRO 基础上进一步降低。

同时，由表1 可以观察到，1-W-DRO 运行结果略低于2-W-DRO 与∞-W-DRO，而后面两者运行结果较为接近。这是由于不同的Wasserstein 距离阶数c对应的是在衡量分布之间的差异时考虑距离的不同乘方。较小的c值更多地关注分布的位置，而较大的c值更多地关注分布的形状［47］。 1-Wasserstein 距离主要关注分布中心或质心的变化，1-W-DRO 模型可能更加关注风电整体或平均偏移。2-Wasserstein 距离除了关注分布位置，还会考虑分布的形状，这可能会导致2-W-DRO 模型更加关注风电波动或变异性。∞-Wasserstein 距离则主要关注分布的极端值，∞-W-DRO 模型主要关心两个分布之间转移的最大可能成本。

另外，由式（25）可知，Wasserstein 模糊集半径随着置信度的增大而增大。当所提模糊集置信度为0%时，∞-Wasserstein 半径为0，此时模糊集认为经验分布即为风电真实概率分布，难以考虑到样本外极端状况，导致决策鲁棒性弱。当置信度趋于100%时，所提模型趋近于RO，决策过于保守使得系统优化运行费用升高。

综上所述，在低半径置信度（如20%或50%）下2-W-DRO 与∞-W-DRO 优化运行成本相同的原因是当半径置信度很低时，模糊集的半径相对较小，这意味着不确定性范围较小。在这种情况下，两个分布中大部分权重较为集中，使得它们之间的平均差异和最大差异都相对较小。因此，2-W-DRO 和∞-W-DRO 结果非常接近或相同。在高半径置信度下的两者结果差异是因为当半径置信度（如70%或90%）增加时，模糊集的半径会增大，模糊集考虑了更大的不确定性范围。因此，∞-W-DRO 模型可能会为了对抗最大不确定性而做出相对保守的决策，从而导致成本稍高。算例结果表明，通过调节模糊集置信度，系统运行成本可有效自适应平衡调度结果的鲁棒性和经济性。

5.5 OLDR-AMFA 求解策略有效性验证

对采用OLDR-AMFA 算法与采用传统样本平均算法（sample average algorithm，SAA）和SLDR 策略及RO 模型的测试系统调度结果进行比较。SAA是随机优化的一个特定方法，主要思想是通过使用大量的随机样本，以由样本得到的经验分布作为随机变量真实分布，从而尝试近似原始的随机优化问题，并求解这个近似问题来获得问题的近似解。表2 展现了所提DDRO 模型通过不同近似算法求解得到的系统调度总成本、所用计算时间及调度方案在样本外数据中的弃风失负荷率。

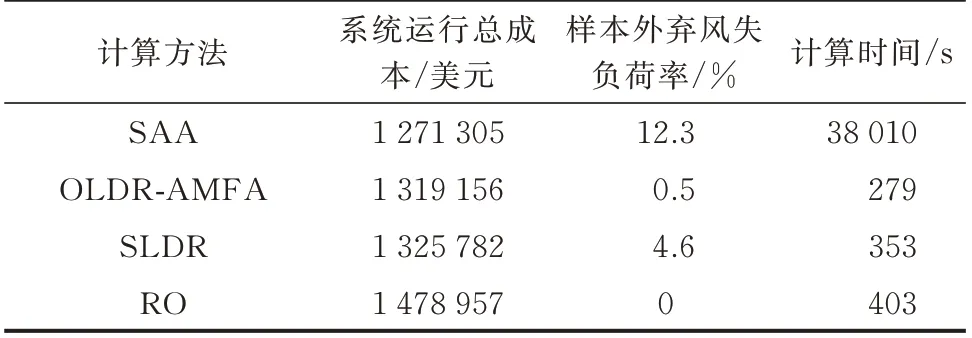
表2 求解结果及计算方法性能对比Table 2 Solution results and performance comparison of calculation methods

所提求解算法计算时间显著低于SAA，稍快于SLDR，有效减轻了两阶段分布鲁棒计算负担。尽管SAA 运行成本最低，但同时也带来了较高的样本外风电场景下的弃风失负荷率。这是由于SAA 所考虑的有限历史样本中难以包括小概率工况，此近似结果鲁棒性较差。本文所提模型相较于SAA 覆盖了更多经验分布外情况，尽管运行成本稍高于SAA 结果，但大幅降低了样本外运行结果的弃风失负荷率。SLDR 近似效果并不理想，所得结果与大部分情况下真实系统运行成本差距较大，且样本外保障能力较弱。尽管RO 调度结果最为鲁棒，但所提OLDR-AMFA 算法得到的运行成本与最保守的RO 调度结果相比降低了11.13%，所得系统总运行成本比SLDR 近似算法和RO 结果都更为经济。这说明所提模型及求解算法不仅有效地克服了传统鲁棒方法决策过于保守的缺点，还相较于传统近似方法结果更为合理，一方面平衡了系统调度结果的鲁棒性和经济性，另一方面提升了模型求解速度和精度。

5.6 模型适用性及扩展性分析

本节旨在探究所提模型在不确定性及大规模系统中的适用性与可拓展性。一方面，面对不同随机变量波动程度验证所提DDRO 模型的适用性，另一方面，在大规模系统中风电场数目增加导致的不确定性维度增大的情况下，验证所提模型及算法的扩展性。

5.6.1 不同比例风电场景模型适用性

本节探究不同比例风电场景下所提DDRO 模型运行结果，验证所提模型在不同比例风电下的适用性与可拓展性。所提模型运行结果如图4 所示，风电装机比例对调度成本的影响可见附录C表C2。

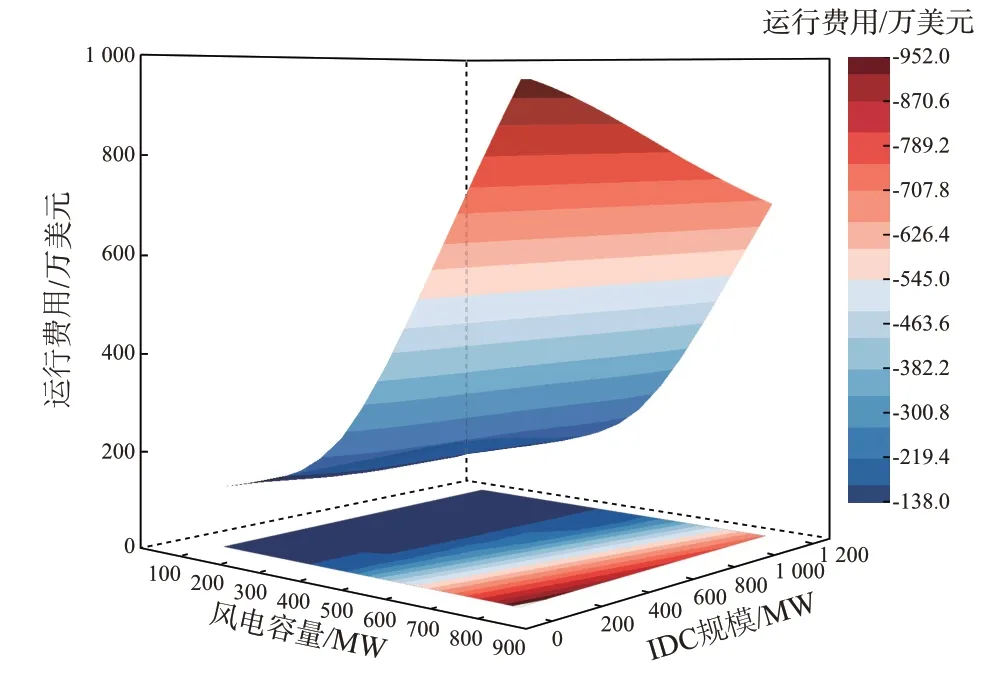
图4 不同风电与ICA 容量下系统运行费用Fig.4 System operation cost under different wind power and ICA capacities

当风电容量固定时，随着ICA 容量的提升，由于弃风量降低使得系统运行成本逐渐降低。当ICA容量固定时，随着风电装机比例逐渐上升，系统总运行成本呈“U”型变化。当风电容量低于100 MW时，随着风电比例的升高，火电机组的运行成本下降。这是由于此时风电比例较低，系统资源灵活性充裕度较高，能够满足平抑风电波动的条件，且系统优先利用清洁风电，经济的风力发电成本替代了部分火电成本，使得系统运行成本小幅降低。当风电装机容量增加至200 MW，即对应风电渗透率低于5.54%时，系统总体运行成本仍无明显上升，而风电装机比例突破200 MW 后，系统总运行成本大幅上涨。不同风电机组装机比例下的电力系统火电运行成本及ICA 用能成本变化较小，总运行成本出现巨大改变的主要原因是风电装机容量突破一定系统比例时，风电波动性及反调峰特性导致火电调节成本大幅上升。

5.6.2 大规模系统模型扩展性分析

为验证本文所提模型和算法的扩展性，选取更大规模改进的IEEE 118 节点系统进行仿真计算，在含有4 个容量为200 MW 的风电场，分别接入节点2、22、41、112，并在节点2、14、30、37、44、109 共引入6 个容量为100 MW 的数据中心，各个数据中心服务器参数相同。

大规模系统模型调度结果见附录C 图C2。ICA 响应量、火电机组调节量负值分别代表ICA 降低自身用电量及火电机组调用向上调节容量，从而平抑风电场发电偏差量。在夜间算力需求低谷时段1—2，风电场实际总出力低于预测值，ICA 将部分算力延迟处理，从而降低系统的净负荷需求，并减少了火电机组向上调节成本，提高系统经济性。在风电场出力预测偏差较大的时段12—17，风电场实际总出力高于预测值，系统内ICA 资源增大运行用电负荷、火电机组向下调节从而降低发电机组出力。根据第1 阶段火电机组的机组组合、调节容量及ICA的用电计划，ICA 和火电机组灵活调整用电计划或机组出力，以适应实际风电情况。

本节通过改变系统中风电装机容量及系统规模，验证了所提模型及求解算法能够有效描述不同规模系统中不同比例可再生能源波动性，并得出调度边界内可行决策。算例表明，所提模型及求解方法在大规模系统中表现出了一定的适用性与扩展性。一方面，尽管由于风电场容量或数目增大，随机变量不确定性波动程度及维度增大，系统内灵活性资源依然有效支撑电力系统安全稳定运行，验证了所提方法的扩展性。另一方面，大规模系统算例求解时长为602 s，相对于应用RO 算法的786 s 的计算时间，所提方法依然表现出了近似算法的计算速度优势，验证了所提方法的适用性。同时，算例说明可再生能源建设需要依据系统实际状况，科学建设集中式不可调资源与分布式资源，从理论层面支撑系统低碳与经济性兼顾的运行策略。

6 结语

针对数据中心集群灵活边界下考虑风电不确定性的电力系统协同优化调度问题复杂情况，本文建立适配风电出力特性的模糊集描述随机变量变化情况，通过调动ICA 响应及火电灵活调节以平抑风电波动，构建考虑风电最劣概率分布下以系统运行成本最小化为目标的电力系统两阶段分布鲁棒优化模型。通过算例验证，探讨了模糊集置信度、不同比例风电场景对所提分布鲁棒优化模型最终运行策略的影响，具体结论如下:

1）为有效挖掘ICA 内部资源灵活性，本文基于ARO 方法提出了一种调度可行域辨识方法，通过所提FAB 模型能够得到ICA 时变最优可行区间，在ICA 整体聚合最优化的同时保证了设备级分解可行性。

2）针对历史数据样本信息构建∞-Wasserstein模糊集描述风电不确定性，相比于区间或矩信息模糊集，所提方法充分考虑了已有数据蕴含的经验分布信息，同时对样本外性能提供保障。算例证明，通过调节模糊集置信度，可以自适应调节决策保守程度，辅助电力系统达成适应调度目标的有效决策。

3）构建两阶段DDRO 协同优化调度模型，并基于修改的IEEE-RTS 24 节点系统验证所提模型方法有效性，最大限度降低弃风失负荷惩罚成本，得到系统日前协同优化调度最优策略，运行结果能够在随机优化的经济性和鲁棒优化的保守性之间取得平衡。

4）提出了OLDR-AMFA 求解方法将DDRO 问题近似重构为商业求解器可直接求解的有限维优化问题，解决了该优化问题固有的无限维求解难题。算例结果表明，所提方法相较于传统SAA 近似结果覆盖更多经验分布外情况，所得方案抗风电随机波动性能力显著增强，渐近最优性优于SLDR 方法，且能够有效减轻计算负担，缩短求解时间。

后续工作可进一步研究适应高比例、高维度风电不确定性特性的不确定集构建方法，研究该类型模糊集与常规风电不确定性集的区别与共性，并在此基础上，探究新型电力系统下可再生能源与灵活资源容量配置方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。