基于时序注意力机制的电动汽车灵活性概率建模

王昊天，刘 栋，秦继朔，史 锐，但扬清，孙英云

（1.华北电力大学电气与电子工程学院，北京市 102206；2.国网经济技术研究院有限公司，北京市 102209；3.国家电网有限公司，北京市 100031；4.国网浙江省电力有限公司经济技术研究院， 浙江省 杭州市 310007）

0 引言

随着大规模新能源与柔性负荷的接入，新型电力系统的随机性、不确定性显著增加，传统“源随荷动”的调节模式正逐步转变为“源荷互动”调节模式［1］。新型电力系统对灵活性资源的需求急剧增加，对系统内各类可调节资源的灵活性进行精确建模具有重要意义［2］。截至2022 年底，中国电动汽车（electric vehicle，EV）保有量为1 045 万辆［3］，预计到2030 年，EV 保有量将达到8 000 万辆［4］。EV 作为一种负荷侧灵活性资源，可以通过调节自身充电功率，向新型电力系统提供灵活性。

虽然单辆EV 可提供的灵活性调节能力较小，但一定规模的EV 经过聚合后，所形成的EV 集群具有较大的灵活性调节能力。现有文献已从多方面对EV 灵活性建模开展了研究［5-7］。文献［8］利用虚拟电池（virtual battery，VB）模型对EV 集群小时级灵活性进行刻画，将单辆EV 边界进行闵氏求和得到EV 集群边界。文献［9］以最小化EV 电费成本与电量差距为目标优化所有EV 充电计划，进一步考虑电量约束计算EV 集群在15 min 时间尺度下的爬坡灵活性。文献［10］基于历史数据分析，利用状态空间模型评估EV 集群的每15 s 调频备用容量。上述文献多以理论最大边界约束EV 灵活性［5-10］，进而进行调度优化［8］。实际上，由于EV 充电行为受电价、用户意愿等多种因素影响［11］，存在多种不确定性，EV 灵活性未必能够达到理论边界。

为刻画EV 灵活性的概率特性，文献［12］利用蒙特卡洛抽样构建EV 状态转移矩阵，分析了99%置信度下的EV 集群灵活性。文献［13］利用高斯过程回归方法获得95%置信度下的EV 集群灵活性边界。文献［14］利用Sigmoid 云模型实现了分时电价与激励影响下考虑响应不确定性的EV 负荷概率分布建模。文献［15］利用最小二乘法拟合EV 出行参数概率分布，评估了分时电价下EV 调度潜力。文献［16］提出基于组合荷电状态的EV 充电负荷概率分布计算方法。然而，上述方法没有考虑电价等影响因素的不确定性，且随着EV 规模增加，采样与计算效率会明显下降。随着人工智能的发展，基于数据驱动的深度学习方法被引入EV 概率建模研究。文献［17］和文献［18］分别利用双向长短期记忆（long short-term memory，LSTM）模型和多层感知机（multi-layer perceptron，MLP）模型刻画EV 出行不确定性。文献［19］将自注意力机制应用于电动汽车充电需求分位数预测。文献［11］利用基于时间模式注意力（temporal pattern attention，TPA）机制的LSTM 模型提取特征关联性，评估价格驱动模式下的可调节潜力。文献［20］结合时序卷积网络（temporal convolutional network，TCN）与Transformer 模型刻画了面向需求响应信号的EV 灵活性。然而，现有文献在建模过程中仅考虑了EV充电行为不确定性［12，16-19］和分时电价［13-15，20］的影响，缺少对实时电价与日前电价之间不确定性的考虑，对灵活性不同时间尺度特征挖掘并不细致［11］。

针对上述问题，本文提出一种基于时序注意力机制的灵活性概率模型（temporal attention mechanism based flexibility probabilistic model，TAM-FPM）。为考虑面向电价的响应不确定性以及EV 充电行为不确定性，本文采用时序注意力机制（TAM）提取时序数据权重，基于TCN 设计多时间尺度特征提取网络挖掘日前电价与实时电价之间不确定性和EV 负荷时序特征，实现EV 灵活性概率建模。

1 EV 灵活性定义

根据国际能源署（International Energy Agency，IEA）的定义，电力系统的灵活性是指电力系统可以根据预期或其他变化来调整电力生产或消费的程度［21］。北美可靠性委员会（North American Electric Reliability Corporation，NERC）将电力系统灵活性定义为利用系统资源满足负荷变化的能力［22］。总之，灵活性可以定义为某种资源在特定影响因素下提供的可调节能力。

本文总结了EV 灵活性的影响因素与表现形式，如表1 所示。影响因素可以分为内在、外在两类。内在影响因素包括开始/结束充电时间、期望充电目标等充电行为；外在影响因素包含受日前电价、实时电价等价格信号，以及调峰指令、调频指令等调控信号和相应市场的激励信号。EV 灵活性具体表现为调峰备用、调频备用以及需求响应等，其可持续时间根据具体形式不同，在2 s～1 h 变动。灵活性一般可以通过可调节功率、可调节速度、可持续时间等指标来描述。由于EV 调节速度较快，本文忽略了可调节速度指标。

表1 EV 灵活性Table 1 Flexibility of EV

首先，利用VB 模型刻画EV 的理论灵活性边界［8］，假设可持续时间τ为1 h。第i辆EV 接入电网开始充电时间为ti，a，离开电网结束充电时间为ti，d，接入电网初始电量为Si，a，期望充电电量为Si，exp，式（1）和式（2）描述了EV 的电量边界，式（3）和式（4）描述了EV 的功率边界，EV 在充电过程中需满足式（1）至式（7）的约束。EV 功率边界与电量边界如附录A 图A1 所示，对单辆EV 的边界进行闵氏求和，即可得到EV 集群的灵活性边界。

为描述EV 灵活性，一般需要选取基线负荷作为对比。基线负荷研究并不属于本文讨论范畴，为了便于对比说明，本文将基线负荷设定为以下场景:在不受价格信号影响的情况下，EV 接入电网立即以最大功率充电，充电至期望电量则停止充电，直至离开电网。在EV 受到价格信号影响后，其灵活性Fi，t可以建模为实际充电负荷Pi，t与基线负荷的差值，如式（8）所示。EV 集群灵活性与集群负荷分别如式（9）和式（10）所示。

式中:Ft为t时刻EV 集群灵活性；N为EV 集群规模；Pt为t时刻EV 集群负荷。

在日前优化中，聚合商可以通过收集EV 数据和市场数据，根据上述模型设定不同的目标函数，通过搭建优化模型得到Fi，t。但是，与发电机组等确定性可调节资源相比，EV 参与电网互动受到多方面的影响，如接入电网时刻、EV 车主参与互动的决策等。这些影响因素受到交通情况和用户意愿的影响，存在较多的不确定性，如充电行为不确定性εt、响应不确定性ελ等。这些不确定性一般可以从历史电价、负荷数据中进行挖掘，可以利用某种概率分布的形式进行描述，如式（11）所示。

假设EV 基线负荷不受外在因素影响，那么EV灵活性概率建模问题就可以转变为EV 实时负荷Pt中上述不确定性的概率建模问题。下面本文选取两种不确定性进行分析。

1）充电行为不确定性

本文将EV 充电行为不确定性εt细分为两类不确定性:第1 类为接入和离开充电桩时间的不确定性；第2 类为提前或延后接入和离开充电桩的不确定性。

不同的EV 用户，如私家车、公交车、出租车等，其充电习惯并不相同［23］。受出行需求影响，私家车一般在小区或公司进行充电，充电频率较低，充电时间与上下班相关。公交车和出租车的充电时间往往具有更强的随机性和不确定性，这属于第1 类充电行为不确定性。

在传统优化模型中，通常假设EV 的日前充电计划保持不变，在实时阶段仍按照日前充电计划进行调度。然而，EV 用户受工作、天气、交通等影响，很可能出现提前接入电网、延后接入电网、提前离开电网或延后离开电网等情况。这属于第2 类充电行为不确定性，如果考虑EV 充电时间提前或延后的不确定性，则传统优化方法难以建模进行求解。

2）响应不确定性

EV 响应不确定性与价格信号、调控信号等外在影响因素有关。受篇幅限制，本文仅针对价格信号影响下的EV 响应不确定性ελ进行分析。日前电价与实时电价统计结果如附录A 图A1 所示，由图可知，实时电价波动性较大，与日前电价存在较大误差。在日前阶段，聚合商基于日前电价优化EV 充电功率，而在实时调度时，实时电价与日前电价并不完全一致，日前优化结果的参考意义受电价不确定性影响极大，两者之间的偏差则会导致日前充电计划的非最优性，使聚合商失去EV 用户的信任难以进行有效调控。因此，准确预测实时电价是降低用户响应不确定性的有效手段。为解决电价不确定性带来的问题，传统优化方法通常设计两阶段优化算法，分别完成日前优化与日内滚动优化，但仍属于确定性优化范畴，难以刻画价格信号影响下响应不确定性对EV 灵活性建模的影响。相比传统优化模型，深度神经网络具有较强非线性拟合能力。

2 基于TAM 的灵活性概率建模

假设X=[x1，x2，…，xd，…，xD]T为D组输入数据，目标输出Ug=[ug，1，ug，2，…，ug，d，…，ug，D]T，每组数据均服从独立分布，其中，xd为第d组时序输入数据，ug，d为第d组真实数据。构建EV 灵活性概率建模网络θ，则EV 灵活性概率建模问题可以构建为寻找最优网络参数θ*，使得目标概率分布在目标Ug处的概率最大，即最大似然估计问题，如式（12）所示。

2.1 TAM

注意力机制是人们在机器学习模型中嵌入的一种特殊结构［24］，相比卷积神经网络（convolutional neural network，CNN）和 全 连 接 网 络（fully connected network，FCN）采用固定参数处理输入数据，注意力权重矩阵能够随着输入数据灵活变化，从而有效反映不同输入特征的贡献程度。然而，传统注意力机制只针对输入特征维度提取注意力权重，难以处理不同时间步之间的时序耦合特征。在现有的TPA-LSTM 中［25］，LSTM 模型输出的隐藏状态变量经过TPA 机制中CNN 固定长度卷积核处理，融合了同一隐藏状态变量的时序耦合特征，辅助LSTM 模型进行下一时间步预测。然而TPA 机制将所有时间步的时序特征融合为一个卷积向量，使得不同时间尺度下的时序特性难以体现，不利于后续网络时序特征处理。同时，LSTM 模型隐藏层状态变量需要根据预测时间步长循环迭代，难以并行计算，影响模型训练效率。

针对此问题，本文从数据的时间维度出发，采用TAM 使得网络在获得不同时间步之间注意力权重的同时，避免对时间维度进行压缩导致信息损失。

首先，假设xd=[x1，x2，…，xm，…，xM]T，其中，M为特征维度，根据式（13）得到TAM 的Q、K、V向量。

式中:xm=[x1，x2，…，xt，…，xT]为第m维特征的时序数据；Q为查询（query）向量；K表示键值（key）向量；V为值（value）向量；WQ为查询矩阵；WK为键值矩阵；WV为值矩阵。WQ、WK、WV可利用神经网络学习其参数。

其次，计算相似度矩阵，再除以时间序列长度的根进行缩放，经过Softmax 函数得到时序注意力权重矩阵α，如式（14）所示。时序注意力权重矩阵α对相同特征向量在时间维度上进行归一化处理。因此，可以代表相同特征向量中不同时间步的注意力权重。

最后，利用α和V相乘，并与原始输入数据xd进行残差连接，得到新的输入数据xnew，作为后续网络输入，如式（15）所示。

所提TAM 相比TPA 机制，并未对输入数据在时间维度上进行压缩融合，而是保留了时间维度原有的尺寸，有利于后续网络提取不同时间尺度特征。同时，在输出位置加入残差连接，使得最终输出数据既融合了不同时序之间权重，也保留了原始数据的特征，避免出现梯度消失问题。

在推进“三农”问题解决的过程中，我国农业产业化水平不断提高，农村市场化程度不断提升，因此，我国农村金融在理财产品和服务、金融信息咨询、信用贷款、担保和资本市场等方面需要更多的服务。但是，农村传统金融模式占据主导地位，信贷产品少，其他消费性金融产品少，不能满足新时期农户在住房、就医、求学等方面的消费性需求。

2.2 TAM-FPM 网络

由于实时电价与EV 实时充电负荷波动性较大，直接使用LSTM 模型难以学习其波动特性。相较于LSTM 模型，TCN 能够以非循环形式处理时序数据，在避免梯度消失/爆炸问题的同时有着良好的并行计算能力［26］。为捕获输入数据在不同时间尺度下的波动特性，提取不同时间尺度时序特征，本文进一步采用不同大小的TCN 设计多时间尺度特征提取网络，如图1（a）所示。3 层TCN 分别设置卷积核大小为3×1、2×1 和4×1，逐步提取短时间尺度、中时间尺度、长时间尺度的时序波动特性。利用1×1 卷积核使3 个时间尺度特征通道保持一致。利用FCN 进行特征融合，压缩不同时间尺度特征向量从输入特征维度至输出特征维度，进一步通过时序反卷积网络使得不同时间尺度特征向量在时间维度上保持一致，获得不同时间尺度输出特征，经过最终1×1 卷积核压缩通道数，获得输出数据的正态分布均值与标准差。

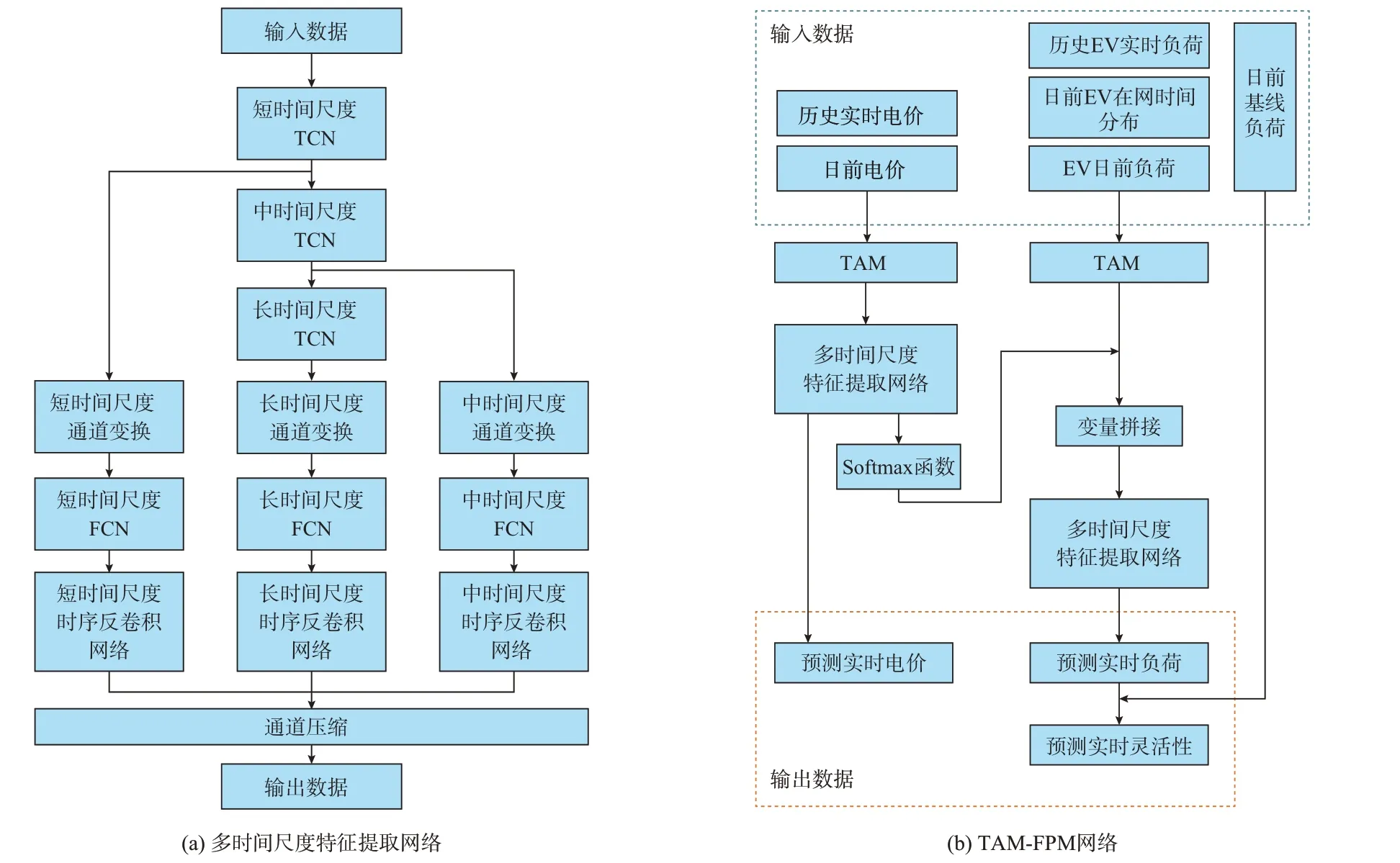
图1 TAM-FPM 结构图Fig.1 Structural diagram of TAM-FPM

结合TAM 和基于TCN 的多时间尺度特征提取网络，本文提出了基于TAM 的TAM-FPM 网络，如图1（b）所示。网络输入数据包括历史7 d 实时电价、日前电价、历史EV 实时负荷、EV 日前负荷、日前EV 在网时间分布。网络输出数据包括预测实时电价、预测EV 实时负荷的均值和标准差。

首先，输入历史实时电价、日前电价、历史EV实时负荷、EV 日前负荷、日前EV 在网时间分布等数据，经过TAM 处理，得到不同时间步之间的注意力权重，融合得到新的输入数据。

其次，利用历史实时电价数据和日前电价数据，预测实时电价的均值与标准差。将预测实时电价的均值作为条件变量，经过Softmax 函数处理后得到电价条件编码，辅助预测EV 实时负荷。

最后，拼接经过TAM 处理后的EV 负荷相关数据与电价条件编码，经过多时间尺度特征提取网络，输出预测EV 实时负荷的均值与标准差。利用输出的概率分布参数进行抽样，可以实现EV 实时负荷的概率建模。通过与日前基线负荷对比，则能够进一步得到EV 灵活性概率建模情况。

2.3 损失函数与评价指标

本文所提模型属于概率预测模型。因此，损失函数采用负对数似然（negative log-likelihood，NLL）函数，如式（16）所示。

式中:LP为网络训练损失函数；uμ，d为输入xd得到的正态分布均值向量；uσ，d为输入xd得到的正态分布标准差。

本文选取平均绝对误差（mean absolute error，MAE）IMAE和均方根误差（root mean square error，RMSE）IRMSE作为确定性建模评价指标，并选取连续等级概率分数（continuous ranked probability score，CRPS）ICRPS、预测区间平均宽度（prediction interval average width，PIAW）IPIAW、预测区间平均覆盖率误差（prediction interval average coverage deviation，PIACD）IPIACD作为概率建模评价指标［27］。

式中:β为置信度；ud和为从基于模型学到分布参数所构建的概率分布中采样得到的预测样本；为置信区间上边界；为置信区间下边界；sgn（·）为符号函数。

3 算例分析

3.1 数据与参数设置

日前电价与实时电价数据来自美国PJM 市场，从2020 年1 月1 日至2020 年12 月30 日，其中，实时电价中高于100 美元/（MW·h）的异常部分均置为100 美元/（MW·h）［28］，训练集采用1 月1 日至11 月4 日的数据，测试集采用11 月6 日至12 月30 日的数据。针对第1 类充电行为不确定性，通过统计分析可知，EV 接入电网开始充电时间ta和离开电网结束充电时间td服从正态分布，通常表现为截断正态分布的形式，以保证抽样数据的合理性［29］。对于EV初始电量与期望电量，也可以假设其服从截断正态分布［29］，具体概率密度函数见附录B。

针对第2 类充电不确定性，由于尚无公开数据参考，本文选取二项分布，在抽样得到EV 日前充电计划的基础上进行仿真模拟［30］。假设pdelay为EV 提前或延后的概率，则EV 提前或延后的充电行为服从附录B 式（B5）和式（B6）所示的二项分布。假设EV 用户接入电网时间不变，相比日前充电计划，存在0.2 的概率延后1 h 离开电网，以模拟第2 类充电行为不确定性。

EV 仿真参数如附录B 表B1 所示［29，31］，最大充放电功率为7 kW，额定电池容量为30 kW·h。本文模拟EV 规模为100 辆，通过蒙特卡洛抽样得到EV日前充电计划参数。EV 日前充电计划、实时充电计划均以充电成本和负荷波动最小为目标，通过Gurobi 求解器搭建模型并求解，时间尺度为1 h，总步长为24，见附录B。

训练集规模为302 组样本，测试集规模为48 组样本。训练次数设为200 次，批数量为128，优化器为Adam，学习率为0.001，权重衰减因子为0.001。本文所提模型基于Pytorch 深度学习框架搭建，详细网络参数见附录C 表C1 至表C3。计算机CPU 型号为Intel i5 8765U，内存为8 GB。为验证本文所提模型的有效性和优越性，本文选取2 种模型进行对比，包括MLP 模型、LSTM 模型。

3.2 训练效果验证

3 种模型损失函数对比如图2 所示。由图2 可知，相比MLP 模型和LSTM 模型，TAM-FPM 在训练过程中损失函数下降更快且更稳定，表明所提网络结构能够有效促进模型收敛。表2 对比了3 种模型在训练集上的预测指标。由表2 可知，TAMFPM 在MAE、RMSE、CRPS 这3 项指标上均取得了最小值，说明所提模型既能够准确地预测，同时也能够准确地描述电价与负荷的不确定性。

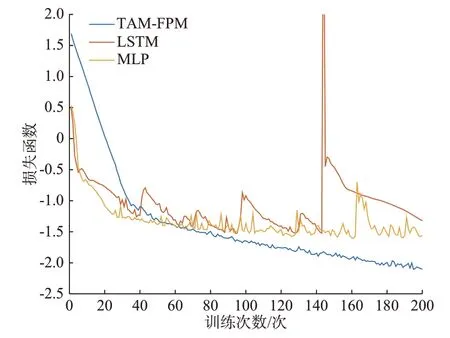
图2 损失函数对比图Fig.2 Comparison diagram of loss function

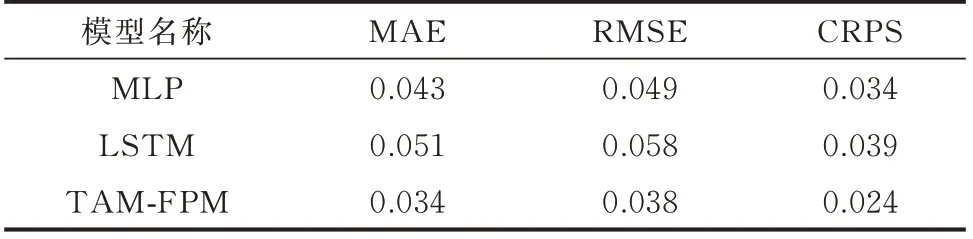
表2 训练集预测指标Table 2 Forecast indicators of training dataset

3.3 灵活性分析

本文进一步验证了所提模型的可靠性与锐度性能。由表3 可知，所提模型在10%～90%置信区间下，均具有最小电价PIACD 指标，并且电价预测PIACD 指标相对更小，说明所提网络结构能够有效提取电价的时序特征，进而提高EV 负荷预测准确度。EV 仅以充电成本为目标会导致负荷波动较剧烈。因此，负荷PIACD 指标相对电价预测指标有所增加，但所提模型的负荷PIACD 指标在10%～80%置信区间均为最小，这也说明TAM-FPM 模型相比其余模型可靠性更高。由表4 可知，所提模型PIAW 指标在10%～90%置信区间下均达到了最小值。综合PIACD 和PIAW 这2 个指标分析可知，TAM-FPM 有着更高的可靠性与锐度性能，能够更精确地反映EV 充电行为的不确定性和响应不确定性。

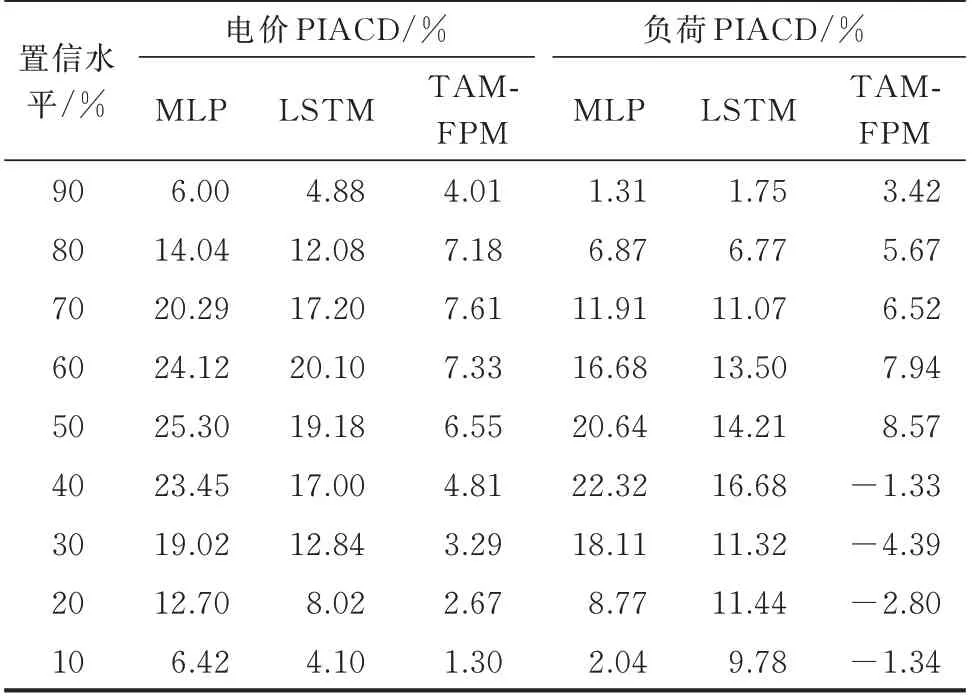
表3 训练集PIACD 指标Table 3 PIACD indicators of training dataset

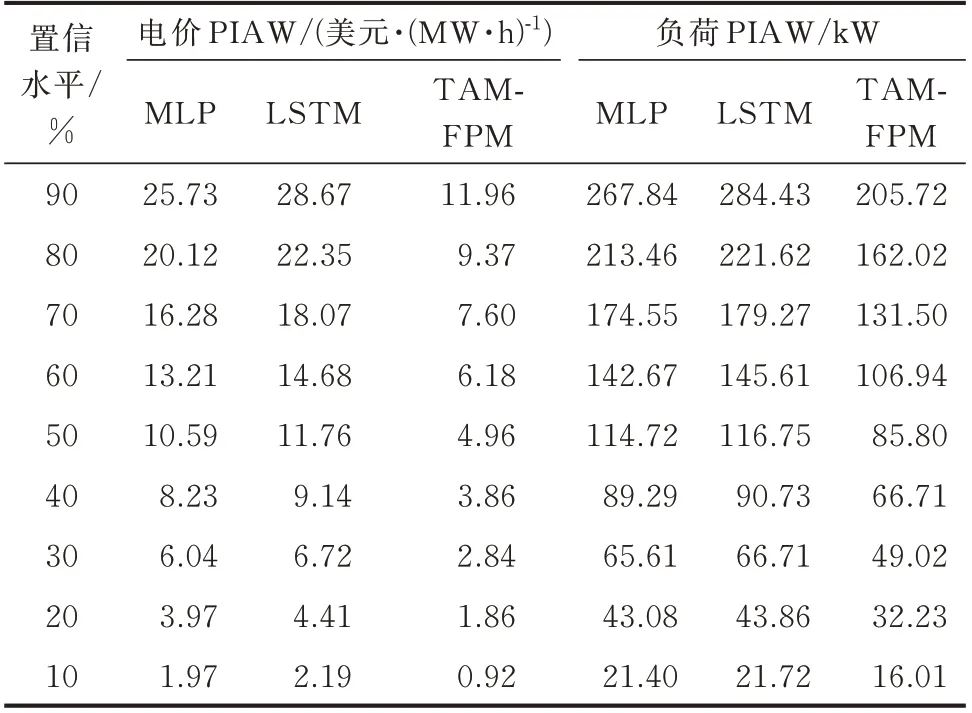
表4 训练集PIAW 指标Table 4 PIAW indicators of training dataset

最后，本文选取测试集中2020 年11 月22 日的电价预测与负荷预测情况进行分析，真实数据如附录C 表C4 所示。在16:00—20:00 时段内，实时电价相对其他时段明显升高，最高实时电价出现在17:00。由图3 可知，MLP 模型预测的最高电价出现在16:00，与实际最高电价存在1 h 的偏差，导致MLP 模型的实时负荷预测最低值出现在了16:00而非17:00。而LSTM 模型没有预测到电价波动趋势，整体变化平缓，2 种对比模型的各时刻PIAW 指标相对更大，难以有效表达实时电价变化情况。因此，难以保证实时负荷概率建模的有效性与可靠性。相比之下，TAM-FPM 在电价平缓时PIAW 指标较窄，在波动时PIAW 指标变宽，并且有效刻画了16:00—20:00 时段内的电价升高趋势以及17:00 时刻的最高电价，说明TAM-FPM 能够根据历史实时电价和日前电价，有效刻画实时电价的不确定性，对于实时电价的概率预测效果更好。得益于此，所提模型在负荷概率建模中各时段负荷PIAW 指标更窄，刻画出与电价强相关的变化趋势，在16:00—19:00 时段，EV 负荷呈现反向下降趋势。这表明本文所提模型既能准确建模实时电价与日前电价之间的偏差，也能根据实时电价概率建模结果，准确可靠地预测实时负荷概率分布。

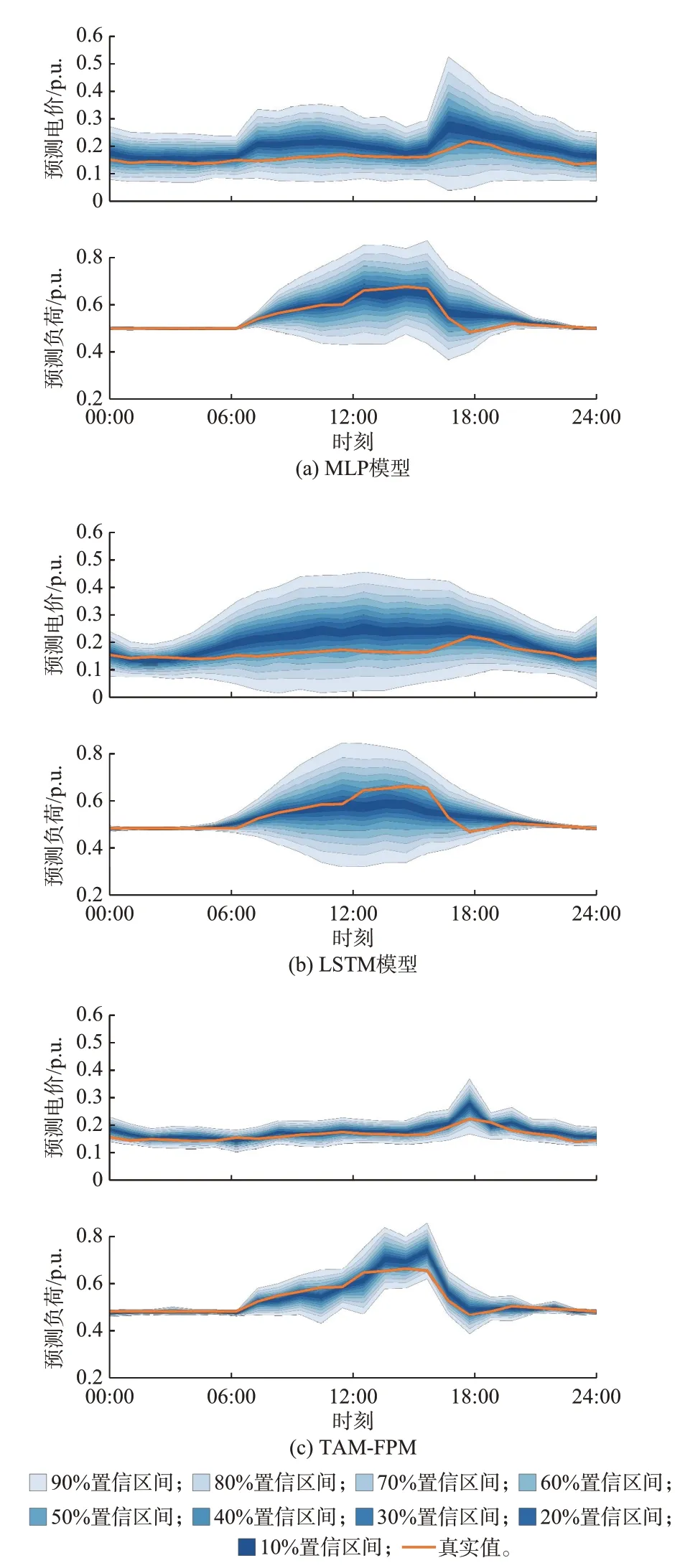
图3 实时电价与EV 实时负荷概率建模效果Fig.3 Probabilistic modeling effect of real-time electricity price and EV real-time load

图4 展示了本文所提模型的EV 灵活性概率建模效果。相比日前基线负荷，在接入电网后，EV 集群受预测实时电价影响，并不立即充电，而是转移至12:00—16:00 时段充电，在07:00—12:00 时段提供了向下的灵活性，在12:00—16:00 时段提供了向上的灵活性。16:00—20:00 时段内电价相对升高，EV 充电负荷迅速下降，接近日前基线负荷，所提供的灵活性也从16:00 开始迅速减小。所提方法刻画的置信区间能够较好地覆盖实时灵活性，这表明本文所提方法能够可靠地进行EV 灵活性概率建模。

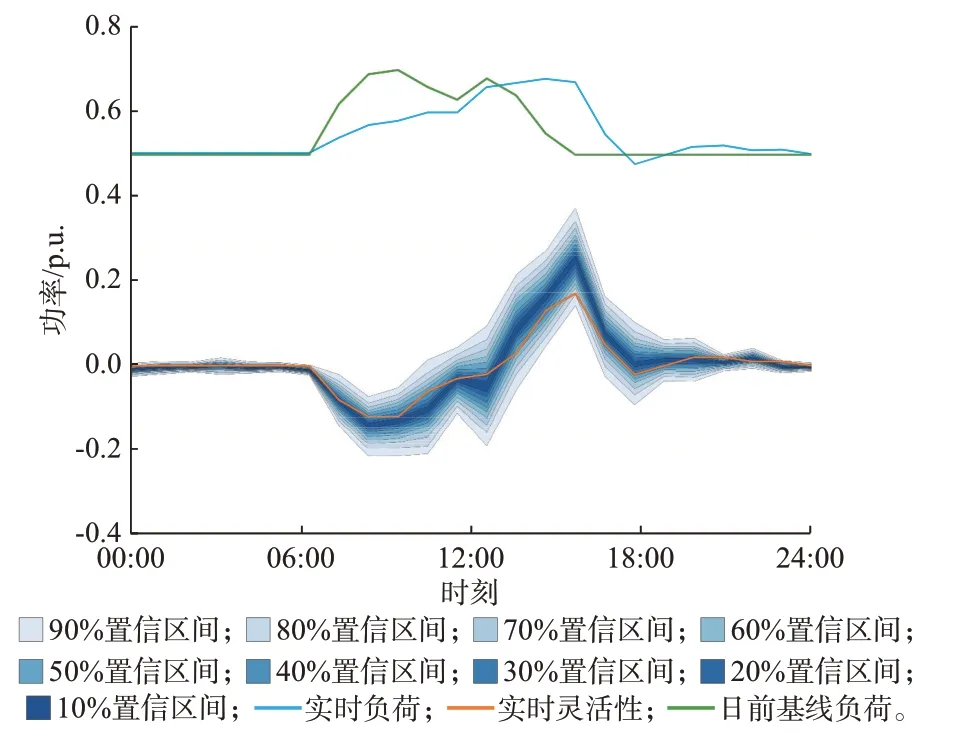
图4 EV 灵活性概率建模效果Fig.4 Probabilistic modeling effect of EV flexibility

4 结语

本文提出了基于TAM 的EV 灵活性概率建模方法，刻画了EV 充电行为不确定性以及受实时电价影响的响应不确定性，实现了EV 充电行为、实时电价等因素与EV 灵活性之间非线性映射关系的概率建模。算例表明，TAM-FPM 利用TAM 和基于TCN 的多时间尺度特征提取网络，准确提取了电价与负荷在多时间尺度下的时序波动特征，提高了模型训练过程的稳定性与收敛性，相比MLP 模型和LSTM 模型具有更高的可靠性与锐度性能，与日前基线负荷对比表明，所提模型对EV 灵活性概率建模更为准确。

本文方法考虑了EV 用户面向电价的响应不确定性，适用于价格型需求响应场景。在不同应用场景下，本文方法也可以用于日前与实时市场价格的不确定性建模，如调峰价格、调频价格。但相比价格型需求响应场景，调峰、调频场景均具有明确的调控指令，还包含调峰出清价格、调频出清价格等形式的市场激励。后续将在本文基础上，进一步研究面向调控指令的响应不确定性建模，刻画调峰、调频场景下EV 灵活性的概率特性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。