触针式表面形貌测量仪探针几何特性引起的失真机理与识别方法

王 康, 皮 磊, 张 树, 张诗涵, 施玉书

(中国计量科学研究院，北京 100029)

1 引 言

触针式表面形貌测量仪(以下简称形貌测量仪)凭借其测量精度高、测量范围大以及对被测工件表面要求较低等优势,在表面粗糙度、几何形状、波纹度等表面形貌结构参数测量中得到了广泛的应用[1～4]。国家标准文件GB/T 6060—2009《接触(触针)式仪器的标称特性》强调了探针的几何特性对仪器的测量精度具有重要影响[5],被测物体的表面形貌结构特征较为明显时,探针能够与被测物体表面充分接触,通过对探针进行反卷积运算和半径补偿等数据处理方式,能够实现被测样本表面的精准再现。

对于探针在形貌测量结果中引起的误差补偿问题,研究重点主要为探针的盲重建方法[6]和对测量数据的针尖半径补偿等方面。例如Tian A L等多种探针形状进行测量接触算法模拟,建立了不同尺寸探针测量时的参数模型[7];Chen S G等提出用迭代矢量法来构造被测物体的表面结构[8];Vorburger T V研究团队分析测量轮廓,以最小二乘法迭代实现针尖半径的求取和补偿分析[9];Lee D H等通过三维模拟和频谱分析进行误差补偿和轮廓重构[10]。尽管上述研究对形貌测量仪测量结果中的误差进行了有效补偿,并取得显著成效;但是随着现代工业技术的不断进步和精密零件加工需求的增长,催生出了更多的复杂表面结构元件,测量结果存在着更为复杂的失真情况。如微机电系统中高深宽比的微沟槽结构,航空航天工业中复杂形体表面的工件,光学仪器中高精度表面的光学元件等,这类元件的表面结构对探针的几何特性十分敏感,因此对于探针在测量过程中由于其几何特性引起的失真,需要进行更为详细和深入的分析。

本文针对于形貌测量仪探针几何特性引起的失真机理进行研究,提出了测量结果中复杂失真的识别方式,并通过实验验证了该方式可以有效实现对几何特性引起的复杂失真的多模态识别,提升了形貌测量仪测量结果的可信度解释。

2 失真机理

2.1 探针几何特性

为保证形貌测量仪探针几何特性的统一,文献[5]对探针标称特性进行了规定:理想的探针形状是1个具有球形针尖的圆锥形,其标称尺寸分别为球形半径:2 μm、5 μm、10 μm;圆锥角:60°、90°。形貌测量仪工作时探针与被测物表面接触情况如图1所示,理论上探针越小其测量精度越高,但随着探针尺寸的减小其在测量时承受的压力不断增加且磨损率越高,因此实际应用中需根据被测表面选取具有不同几何特性的探针。由于不存在理想状态下无限小的探针,受球形针尖和圆锥的影响,测量时接触点Q的坐标同球心O的坐标在X轴和Z轴方向存在Δx和Δz的差异[11],传感器在探针沿X轴方向移动过程中对被测零件表面进行离散化采样,记录探针在Z轴方向位移。尽管经校准的传感器带有上述方向的补偿算法,但由于探针几何特性和被测表面形貌的复杂性,传感器测量值不能反映探针的真实位移,该差异是导致测量结果中存在探针几何特性引起的失真的主要原因。

图1 探针测量示意图Fig.1 Probe measurement schematic diagram

2.2 失真的固有存在

形貌测量仪工作原理如图2所示:探针沿X轴方向匀速运动,同时与被测表面保持接触状态;由于被测表面形貌的变化导致探针在Z轴方向发生位移;传感器识别和记录探针球心位置的移动轨迹从而得到被测表面形貌。测量形貌受探针几何函数与被测表面函数共同作用影响[12],采集到的形貌包含探针几何特性的影响,如图3所示,直接对所测形貌进行评定会导致测量结果相较于真实形貌发生“膨胀”。扫描轮廓函数o(x,z)可表示为探针几何函数i(x,z)与被测表面函数h(x,z)的卷积运算,计算方式见式(1):

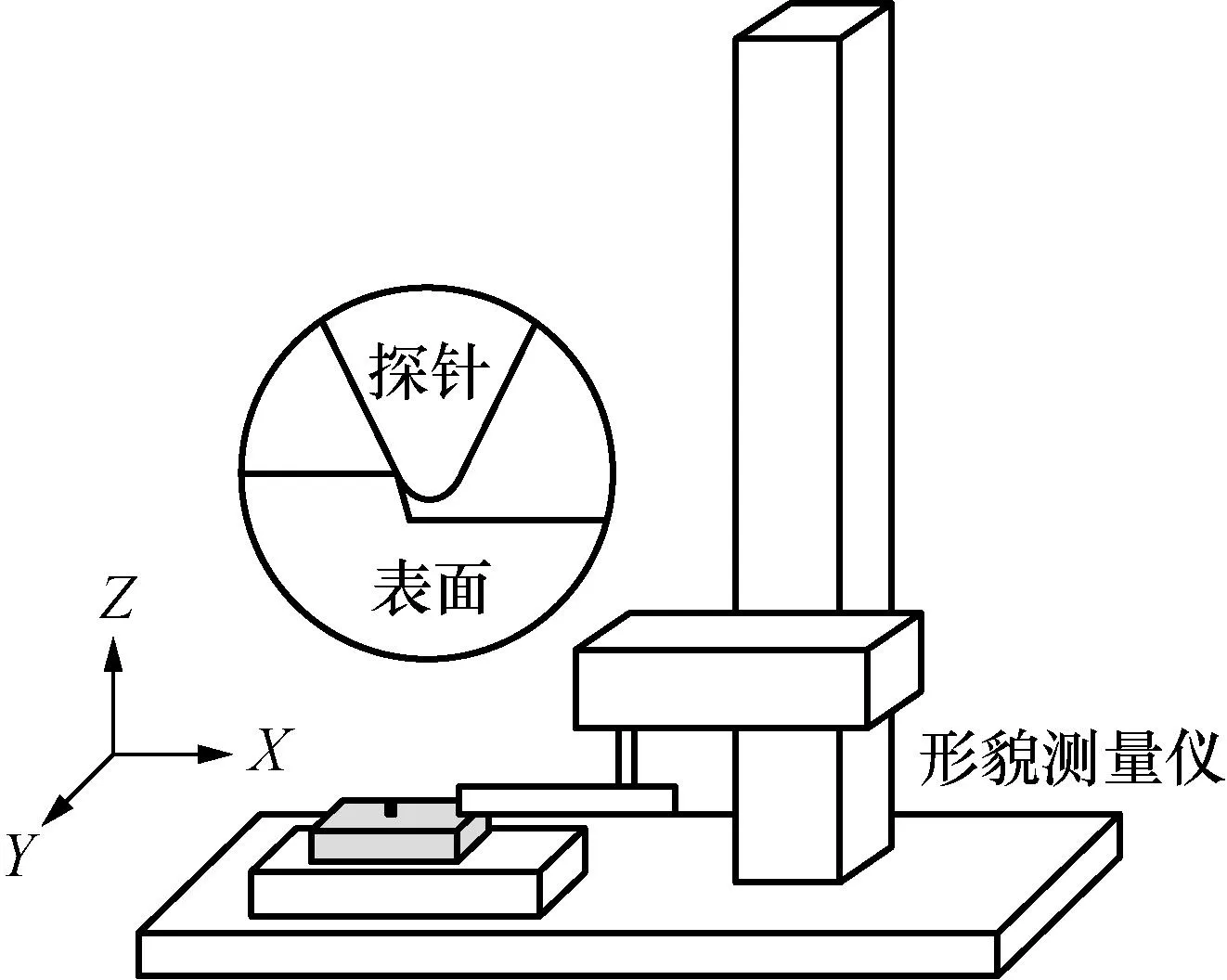
图2 形貌测量仪工作原理Fig.2 Principle of topography measuring instruments

图3 被测形貌与真实形貌对比Fig.3 Comparison between measured profile and actual profile

o(x,z)=i(x,z)*h(x,z)

(1)

失真由探针几何特性和形貌测量仪系统原理所引起,因此形貌测量仪的所有测量过程均伴随着失真,并且失真包含多种情况,对失真情况进行准确识别有助于对测量结果的解释和校正。

2.3 失真分类

2.3.1 典型失真

在形貌测量仪工作过程中最主要且普遍的一种失真是由探针球形针尖引起的单一类型失真,如图4所示,球形针尖半径的存在导致采集到的被测表面形貌实际为针尖球心运动轨迹,并非被测表面实际形状,将该类型失真称为典型失真。

图4 典型失真Fig.4 Conventional distortion

2.3.2 复杂失真

将典型失真外的失真称为复杂失真,该失真可能由探针几何特性、被测表面形貌等多种因素引起[13],由探针几何特性引起的复杂失真根据不同特点主要可划分为以下3种:

1) 探针几何特性中的球形针尖半径和锥角限制了对表面形貌较大峰谷的测量,如图5所示球形针尖不能与被测表面始终保持接触,接触点从球形针尖过渡到圆锥部分,具体表现为将大型峰谷的上升沿和下降沿扫描成直线轮廓,从而丧失了该测量位置的斜率信息。

图5 较大峰谷复杂失真Fig.5 Complex distortion of large peaks and valleys

2) 几何特性中的球形针尖半径限制了对较小峰谷的测量,如图6所示,具体表现为将小型尖峰和深谷轮廓扫描为光滑轮廓,从而丧失了该测量位置的深度和高度信息,此时扫描得到的表面形貌已严重偏离真实表面形貌。

图6 较小峰谷复杂失真Fig.6 Complex distortion of small peaks and valleys

3) 此外由于探针加工误差和使用时的磨损,探针真实几何形状并非理想状态,而是如图7所示,其几何特性未满足标称要求,该失真将影响被测表面形貌整个测量过程。

图7 探针真实形状与理论形状Fig.7 Theoretical shape and actual shape of probe

本文着重阐述测量大峰谷情况时探针几何特征所引起的复杂失真识别方式和对测量结果进行复杂失真评价。

3 识别方法

3.1 失真识别原理

探针几何特性导致的失真存在于整个测量过程,因此如何实现对典型失真和不同复杂失真的识别十分重要。目前与形貌测量仪相配套的评价分析软件默认原始测量数据带有探针几何特性中球形针尖引起的典型失真[14],并且数据处理时包含对典型失真的校正,但忽略了对探针几何特征相关的复杂失真的识别。

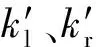
(2)

图8 复杂失真时接触情况Fig.8 Contact situation during complex distortion

超过球形针尖和圆锥交点T后为圆锥部分与被测物表面相接触,探针在X轴和Z轴方向产生的位移不再仅由球形针尖引起,此时形貌测量仪输出结果为带有复杂失真的表面形貌数据。

3.2 识别方法分类

从多个角度特征对事物进行描述,通过综合分析得到最终结果为多模态的一种表述形式[15,16]。将形貌测量仪根据探针球形针尖半径特征进行失真识别的方式称为单模态识别;将根据探针几何特征或其他多种特征相结合的识别方式称为多模态识别。形貌测量仪通过输入探针几何参数实现失真识别,该方式未对测量数据进行详细失真分类,而是将各种失真情况均视为典型失真进行单模态识别。

探针几何特征在大峰谷测量时引起的复杂失真多模态识别方式可通过基于最小二乘法的斜率计算实现。表面形貌曲线由多个采样点构成,无法直接计算测量点Q处切线斜率,通过式(3)以最小二乘法构造拟合曲线从而获取测量点切线斜率k:

(3)

式中:点(xi,zi)为包含测量点Q在内的共n个数据点坐标;测量点Q的坐标(xQ,zQ)位于中间位置;n的选取由形貌测量仪采样频率和探针移动速度所决定。最小二乘法拟合时需要考虑数据量的影响[17,18],当探针在X轴方向位移为探针球形半径时,此位移距离内测量所得数据量能够较好反映中间位置测量点切线斜率,可避免数据量过少导致拟合误差较大;同时也能避免了数据量过多拟合其他位置表面结构特征。形貌测量仪的采样频率为fs,探针在X轴方向运动速度为vx,当位移为探针球形半径R时,其采样点数量n由式(4)计算得到:

n=Rfs/vx

(4)

图9 失真不同区域表示Fig.9 Different region representation of distortions

该类型的复杂失真数据可通过被测点切线与X轴所成夹角β(βl、βr)和半锥角α(αl、αr)的关系进行判别,判别公式为式(5):

(5)

将β角度转换为可求取的切线斜率k,不同类型数据点的斜率k同探针半锥角α(αl、αr)存在如式(6)关系:

(6)

复杂失真数据识别总体流程如图10所示,首先选取包含目标测量点在内的共n个数据点;通过最小二乘法拟合计算该点的切线斜率k;同失真区的上下限作对比从而判断数据点类型,如果为复杂失真数据点,则用拟合值取代该点数据以提高下一个数据点切线斜率的准确性;之后判断是否将所有数据处理完毕,重复上述过程直至记录完毕各测量数据点的失真情况。

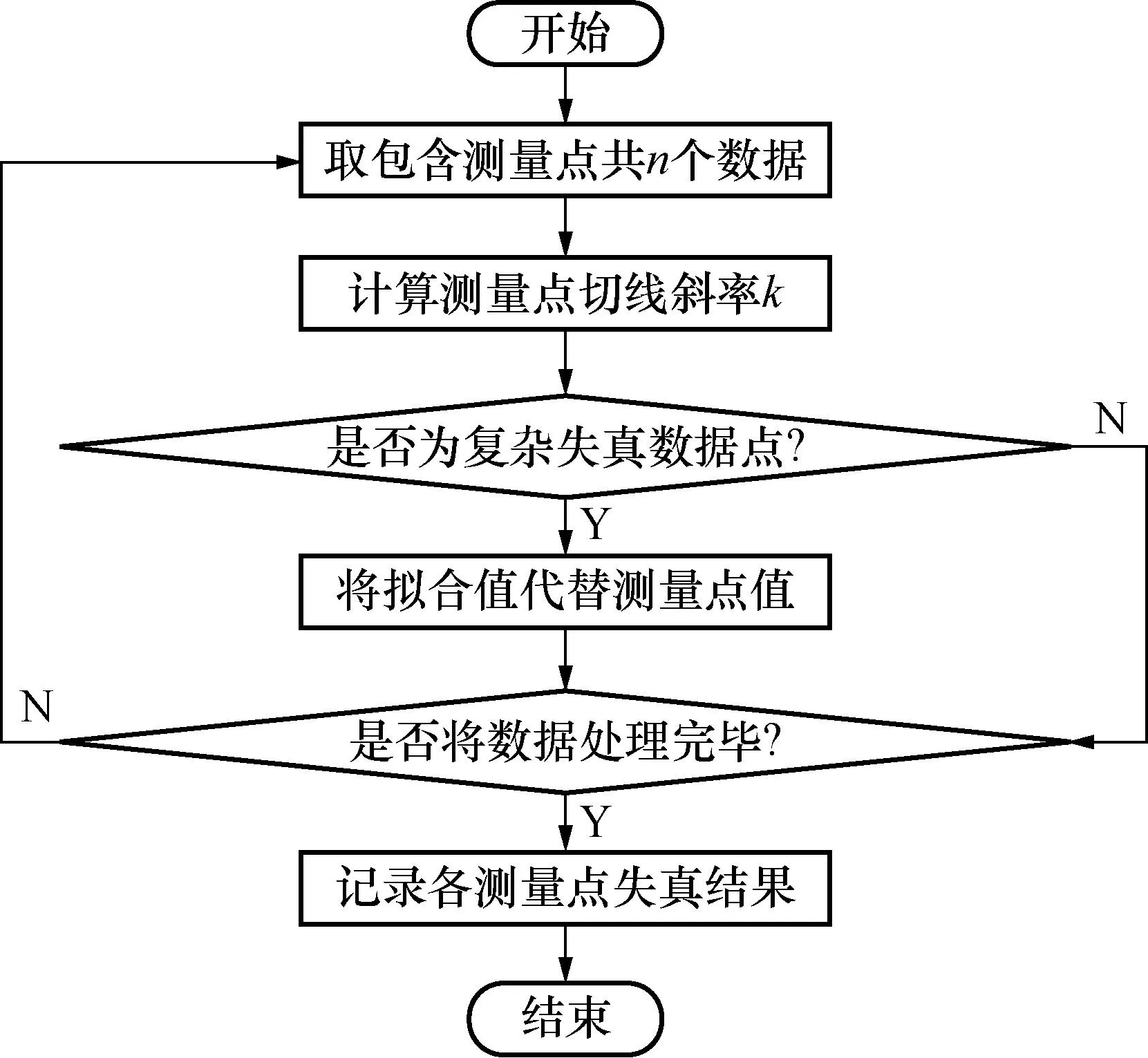
图10 复杂失真数据识别流程Fig.10 Complex distortion data discrimination process

复杂失真情况体现了形貌测量仪测量结果的可信度,反映出测量系统的准确性和稳定性,如果复杂失真数据较少,说明测量结果与真实值接近,可信度较高;反之说明测量结果与真实值存在较大的偏差,可信度较低。

4 实验验证与数据分析

为了验证形貌测量仪单模态识别典型失真的能力和多模态识别复杂失真方法的可行性,结合实验室现有条件使用英国泰勒·霍普森品牌FTS120-4717表面粗糙度仪对不同标准角度块和不同表面形貌样块进行测量分析。测试前使用微观表面特征尺寸测量仪对该表面粗糙度仪探针的几何特性进行测量记录,将被测探针按照表面粗糙度仪工作时位移方向水平放置在载物台上,测量结果如图11所示,探针左侧半锥角αl值为35.1°,右侧半锥角αr值为34.3°,球形针尖半径R为2.037 μm。

图11 探针几何特性Fig.11 Geometry characteristic of the probe

4.1 典型失真的单模态识别

为验证形貌测量仪测量过程中对典型失真的单模态识别能力,分别对角度值为10°、47°、50°、55°、57°和90°的角度块进行测量。将标准角度块水平放置于探针左侧,探针与角度块斜面接触后启动仪器测量(测量90°量块时探针起始位置与量块顶部水平表面接触),探针沿X轴正方向、Z轴负方向移动同时记录量块斜面形貌结构,对各量块分别进行6次测量,每次测量长度为0.3 mm,记录数据并求取斜面轮廓线与水平面所成角度,其测量结果如表1和图12所示。

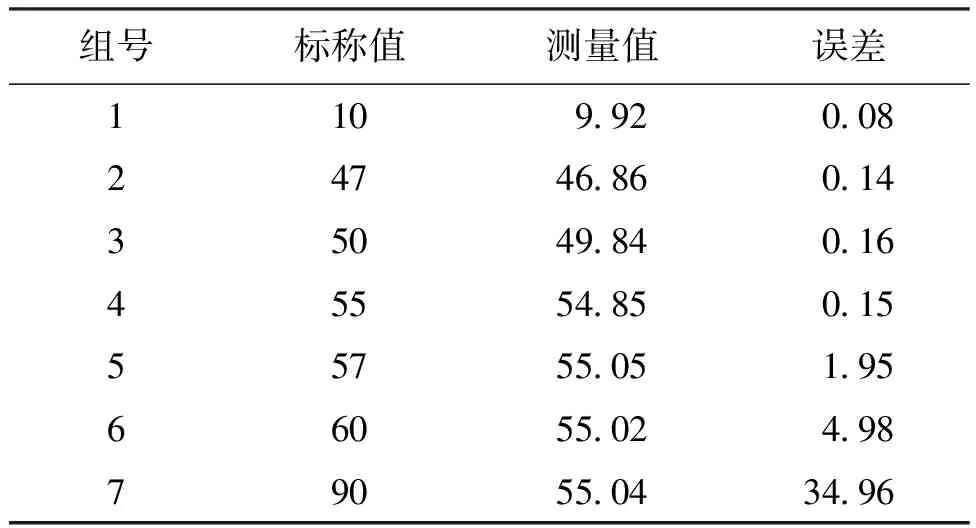
表1 不同角度块测量值Tab.1 Measurements of different angle blocks (°)

图12 不同角度块测量值Fig.12 Measurements of different angle blocks

由实验数据可知,被测点切线与水平面所成夹角βl小于54.9°时形貌测量仪可以识别出典型失真,评价分析软件输出的被测表面形貌角度值与真实值差异小于0.2°;当被测点切线所成夹角βl大于54.9°时形貌测量仪无法对复杂失真实现有效识别,其测量结果不能准确反映被测物真实表面形貌。因此目前广泛使用的形貌测量仪具备单模态识别典型失真和半径补偿的能力,对于复杂失真的识别功能仍具有改进空间。

4.2 复杂失真的多模态识别

测量结果的失真情况对粗糙度参数具有重要影响[19],为验证该算法对复杂失真的多模态识别能力,取不同加工工艺标准样块进行测量并进行算法分析。使用形貌测量仪分别对粗糙度Ra=12.5 μm的粗糙度样块、普通金属加工表面、90°角度块进行测量,记录其轮廓线并对其进行复杂失真的多模态识别。图13展示了识别结果,该图中左侧为表面形貌测量结果,右侧为选取部分测量点切线斜率数值,其中红色数据点为复杂失真数据点,黑色数据点为典型失真数据点,各样块复杂失真情况如表2所示。由测量结果可知,该识别方式具有多模态识别复杂失真的功能,为表面形貌测量提供了复杂失真评价方式。实验中标准样块复杂失真数据点极少,占比仅为0.36%,其影响可忽略不计;普通金属加工表面复杂失真为8.39%,使用形貌测量仪测量其表面参数时需考虑复杂失真数据的影响;90°标准角度块垂直部分均为复杂失真数据,符合模型计算结果。标准样块用于测量设备校准,对表面形貌具有严格要求,通过电化学抛光、等离子喷涂、激光烧蚀等表面处理技术以确保样块具有极高的精确度和一致性;普通金属加工表面受限于加工技术或实际使用需要,使用铣削、磨削和喷涂等传统的材料移除和表面处理技术,因此其表面形貌存在更多不确定性。

表2 三种样块复杂失真情况Tab.2 Complex distortion situations of three types of samples

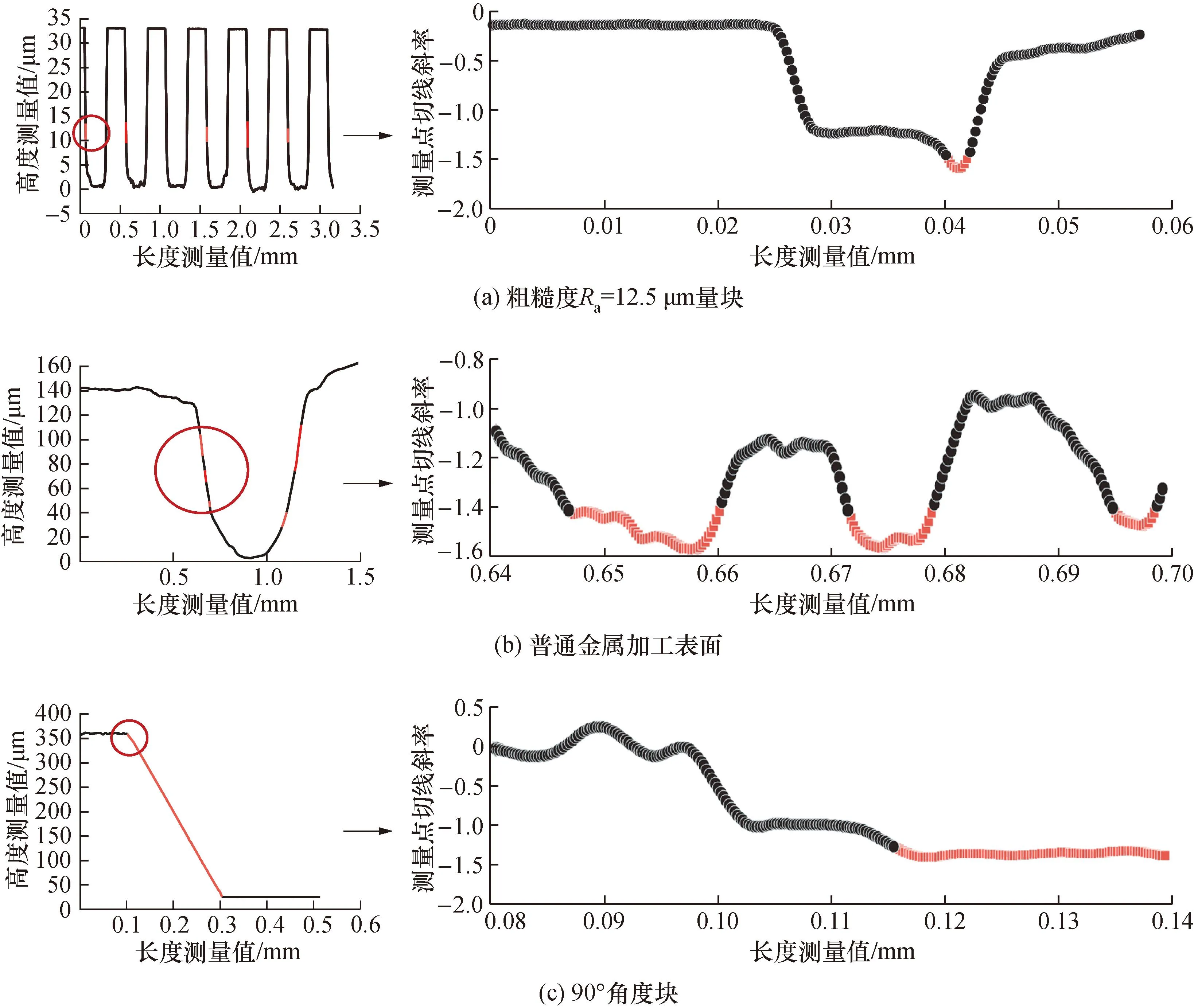
图13 复杂失真识别结果Fig.13 Complex distortion recognition results

虽然标准样块的加工方式确保了较少的复杂失真数据点,测量结果可信度较高,但在实际的生产加工或测量过程中,部分普通器件表面形貌测量时复杂失真数据占比较大,该部分数据对最终测量参数的影响不可忽视。尤其在进行精密光学元件制造、复杂微结构表面测量和其他涉及表面形貌结构参数的领域,更需要关注该部分复杂失真的影响。因此需要根据具体被测表面的特性选取更加适宜的测量方式,对测量结果进行合理评价,避免复杂失真占比过高导致测量表面形貌结果与真实表面形貌差距过大。

5 结 论

针对于触针式表面形貌测量仪测量过程中探针卷积效应导致的失真问题,本文以探针几何特性引起的失真机理为依据,提出了一种多模态识别复杂失真的方法,并进行了典型失真的单模态识别及复杂失真的多模态识别的实验分析。

形貌测量仪的测量结果存在由探针几何特性引起的失真现象,需通过补偿算法进行数据处理,形貌测量仪仅有单模态识别探针球形针尖引起的典型失真的能力,通过探针几何特性设计的多模态识别方法可以有效解决该复杂失真的识别问题。该方法为进一步提高形貌测量仪的测量能力、提升补偿算法还原真实形貌准确性提供了理论支持,通过对形貌测量仪评价分析软件中对应复杂失真的数据处理部分进行算法补充,从而有助于工业测量准确性的提升和增加复杂表面测量结果的可信度。本文给出了实际测量过程中探针与被测表面交互过程一种失真的识别问题,对于复杂失真的多模态识别方法和还原方法仍有进一步研究空间。